Longshore Current Yang Ditimbulkan Oleh

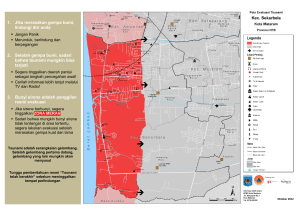
METODE PENELITIAN
Waktu dan Lokasi Penelitian
Kegiatan penelitian dilakukan dengan menganalisis data hasil sounding
ADCP (Acoustic Doppler Current Profiler), Current Meter, konversi angin dan
Tide and Wave Gauge. Kegiatan penelitan ini merupakan salah satu program
penelitian dari Pusat Penelitian Oseanografi (P2O) LIPI untuk mengatasi dampak
abrasi yang sedemikian besar di daerah Eretan Kulon, Indramayu.
Pengambilan data lapangan dilakukan pada 3 periode yaitu pada Bulan
Februari 2006, Mei 2006, dan Agustus 2006, periode ini diharapkan dapat
menjadi gambaran untuk setiap perubahan musim. Perubahan yang disebabkan
pergantian musim diharapkan dapat menjelaskan mengenai transformasi
gelombang dan pola arus menyusur pantai selama satu tahun.
Penelitian dilakukan di pesisir Eretan yang secara geografis berada pada
posisi 6o18’40”-6o20’00” lintang selatan dan 108o04’00”-108o05’45” bujur timur,
berada di Kabupaten Indramayu yang merupakan salah satu kabupaten di daerah
pantai utara Jawa Barat, Gambar 13.
Perolehan Data
Data yang diperoleh melalui penelitian yang dilakukan bersama-sama
dengan Kelompok Peneliti Fisika - Pusat Penelitian Oseanografi (P2O) LIPI,
Jakarta.
Alat pengukur arus dan gelombang ditempatkan pada dua buah mooring /
tripod (Gambar 14), yang ditenggelamkan selama satu minggu dalam setiap
periode pengambilan data (Gambar 15), alat digantungkan pada kaki-kaki
mooring. Mooring I di tempatkan pada jarak 500 m dari pantai, sedangkan
moooring II ditempatkan pada jarak 1000 m dari pantai. Kedua mooring
membentuk garis tegak lurus terhadap pantai. Alat-alat ini (Lampiran 1) merekam
data selama satu minggu dengan interval 10 menit, sehingga akan mendapatkan
data secara periodik selama satu minggu.
Gambar 13. Peta Lokasi Penelitian
25
Current Meter
Tide and Wave Gauge
3m
8m
3,5 m
Gambar 14. Skema Bentuk Mooring
Peralatan yang di pergunakan dalam penelitian secara detail ditabulasikan
pada Tabel 2:
Tabel 2. Alat-alat yang Digunakan dalam Penelitian
Alat dan Bahan
Tipe
Perolehan Data
Alat :
Bathimetri
Arus
Kecepatan
Arah Arus
Acoustic Doppler Current
Profiler (ADCP)
ADCP Furuno Model Cl-35h
Current Meter
RCM 108
GPS
Garmin SRV II
Garmin Map 276 c
Posisi
Tide and Wave Gauge
Model 20-03
Arus Pasang Surut
Gelombang
Bahan :
Peta Rupa Bumi Indonesia
(RBI)
Hardware dan Software
Komputer
(MS. Excel, Surfer,
RCPWave, WRPLOT view,
Map Info dan Arc View )
Peta dasar
Analisis Data
Gambar 15. Diagram Alur Pengukuran Parameter Oseanografi di Eretan Kulon, Indramayu
27
Pengukuran Kedalaman Perairan dan Batimetri
Kedalaman perairan dan batimetri didapat dengan menggunakan ADCP
(Acoustic Doppler Current Proppeler) yang menyapu lokasi penelitian. Daerah
tersebut diplotkan dalam peta digital guna mendapatkan gambaran kedalaman
laut. Penyapuan dilakukan sepanjang garis pantai eretan kulon (sekitar 2 km) dan
ke arah laut lepas sekitar 1,5 km dari pantai.
Data Arah dan Kecepatan Angin
Data arah dan kecepatan angin diperoleh dari Stasiun Meteorologi Jatiwangi
(SM Jatiwangi). Data angin diperlukan untuk memprediksi gelombang laut dalam
berdasarkan data angin maksimum bulanan selama 10 tahun. Data tersebut cukup
representatif
untuk
memprediksi
gelombang
dan
pengaruhnya
terhadap
pembangkitan arus dan transpor sedimen menyusur pantai
Pengukuran Gelombang
Pengukuran gelombang dengan menggunakan instrumen Tide and Wave
yang dipasang pada Mooring selama 7 hari. Hasil pengukuran dikoreksi dengan
menggunakan gelombang hasil dari penurunan angin.
Pengukuran Arus
Kecepatan arus dengan menggunakan instrumen Current Meter yang
dipasang pada Mooring selama 7 hari. Hasil pengukuran dikoreksi dengan
menggunakan nilai kecepatan arus hasil dari perhitungan Gelombang.
Analisis data
Analisis data dilakukan mencakup transformasi gelombang di perairan
dangkal, dan distribusi tegak lurus pantai untuk arus menyusur pantai (longshore
current).
28
Kedalaman
Kedalaman yang diperoleh di lapangan diplotkan ke dalam peta digital
berdasarkan posisi GPS untuk membuat peta kontur kedalaman. Kedalaman yang
diplotkan terlebih dahulu dikoreksi terhadap MSL (mean sea level) sebagai titik
referensi dengan menggunakan persamaan berikut:
Δd = dt – ( ht – MSL)
dimana:
Δd
(1)
= Kedalaman suatu titik pada dasar perairan;
MSL = Permukaaan air laut rata-rata;
dt
= Kedalaman suatu titik pada dasar laut pada pukul t;
ht
= Ketinggian permukaan air pasut pada pukul t.
Peta kedalaman yang diperoleh, dianalisis untuk mengetahui kemiringan
pantai pada tiap profil yang ditentukan dan membandingkannya dengan peta
kontur kedalaman dari Dishidros (1991). Data kemiringan pantai dari Dishidros
digunakan sebagai data awal untuk menganalisis perilaku gelombang dan
pengaruhnya terhadap pembangkitan arus menyusur pantai.
Parameter Gelombang
Peramalan Gelombang
Sebelum perhitungan prediksi (peramalan) gelombang, terlebih dahulu
dilakukan analisis perhitungan panjang fetch efektif (Feff) dan data angin yang
diperoleh dari SM Jatiwangi, Indramayu
Perhitungan panjang fetch efektif menggunakan Peta RBI dan Peta Alur
Pelayaran dengan persamaan:
Feff =
∑ Xi cosα
∑ cos α
(2)
dimana: Xi = Panjang fetch yang diukur dari titik observasi gelombang
sampai memotong garis pantai.
α
= Deviasi pada kedua sisi (kanan dan kiri) arah angin
dengan menggunakan pertambahan 5o sampai sudut 45o.
Metode ini didasarkan pada asumsi sebagai berikut :
a. Angin berhembus melalui permukaan air melalui lintasan yang berupa garis
lurus.
29
b. Angin berhembus dengan mentransfer energinya dalam arah gerakan angin
menyebar dalam radius 45o pada sisi kanan dan kiri dari arah anginnya.
c. Angin mentransfer satu unit energi pada air dalam arah dan pergerakan angin
dan ditambah satu satuan energi yang ditentukan oleh harga kosinus sudut
antara jari-jari terhadap arah angin.
d. Gelombang diabsorpsi secara sempurna di pantai.
Berdasarkan data angin maksimum yang diperoleh dari SM Jatiwangi yang
diukur di darat, maka perlu dikoreksi menjadi data angin di laut untuk dapat
digunakan dalam peramalan gelombang. Urutan analisis koreksi data kecepatan
angin berdasarkan petunjuk dari CHL (2002) sebagaimana disajikan pada Gambar
16 - 19. Dalam memudahkan pembacaan data arah dan kecepatan angin, maka
divisualisasikan dalam bentuk tabel dan diagram mawar angin (wind rose) setiap
bulan selama periode peramalan dengan menggunakan software WRPLOT view
versi 5.3.0.
Gambar 16. Diagram alir koreksi kecepatan angin (simbol lihat dalam teks).
Keterangan: UL = kecepatan angin di darat; UW = kecepatan angin di laut;
RT = kondisi atmosfer; UA = faktor tegangan angin
30
Gambar 17. Rasio Koreksi Angin pada Ketinggian 10 m.
Gambar 18. Rasio durasi kecepatan angin (Ut) pada kecepatan 1 jam (U3600).
Gambar 19. Perbandingan/rasio (RL) kecepatan angin di atas laut (UW) dengan
angin di darat (UL) (CHL, 2002).
Keterangan : Pemakaian RL, normalnya jika jarak alat pencatat angin 16 km dari
laut
31
Peramalan
gelombang
dimaksudkan
untuk
mengalihragamkan
(transformasi) data angin menjadi data gelombang. Di dalam perencanaan
bangunan pantai diperlukan data gelombang yang mencakup seluruh musim,
terutama pada musim dimana gelombang-gelombang besar terjadi.
Salah satu metode peramalan gelombang adalah metode yang dikenalkan
oleh Sverdrup dan Munk (1947) dan dilanjutkan oleh Bretschneider (1958),
metode tersebut di kenal dengan metode SMB (Sverdrup Munk Bretschneider)
(CERC 1984), yang dibangun berdasarkan pertumbuhan energi gelombang.
Kecepatan angin yang digunakan adalah kecepatan angin maksimum yang dapat
membangkitkan gelombang, yakni kecepatan ≥10 knot dari arah utara, barat laut,
barat, timur dan timur laut, sedangkan arah lain tidak dihitung karena berasal dari
darat.
Parameter gelombang perairan dalam dari metode SMB adalah:
Tinggi gelombang signifikan:
U A2
g
2
U
dan H s = 0.243 A ; untuk F* > 2 x 104 (fully developed waves)
g
Periode puncak signifikan gelombang:
H s = 1, 6 x10−3 F*0,5
Ts = 0, 2857 F∗1/ 3
UA
g
(1)
(2)
(3)
UA
; untuk F* > 2 x 104 m (fully developed waves) (4)
g
Durasi pertumbuhan gelombang:
dan Ts = 8.13
t = 68,8 F∗2 / 3
UA
g
(5)
UA
; untuk F* > 2 x 104 m (fully developed waves) (6)
g
g F e ff
Dalam hal ini, F ∗ =
= fetch tak berdimensi; UA = faktor tegangan angin;
U A2
dan t = 7,15 x10 4
t = durasi pertumbuhan gelombang (detik); Feff = panjang fetch efektif (m);
g = percepatan gravitasi (m/det2).
Analisis parameter gelombang diselesaikan dengan menggunakan teori
gelombang amplitudo kecil (small- amplitude wave theory). Berdasarkan teori ini,
32
untuk penyederhanaan rumus-rumus gelombang maka dilakukan klasifikasi
gelombang berdasarkan kedalaman, sebagaimana dalam Tabel 3 (CHL, 2002)
Tabel 3. Persamaan Parameter Gelombang Amplitudo Kecil (CHL, 2002)
Perairan
Dangkal
Kedalaman Relatif
Perairan Transisi
1 d 1
< <
25 L 2
d
1
<
L 20
Kecepatan
gelombang
C=
L
= gd
T
C=
L = T gd = CT
Panjang gelombang
C g = C = gd
Kecepatan grup
L gT
⎛ 2πd ⎞
tanh⎜
=
⎟
T 2π
⎝ L ⎠
L=
gT 2
⎛ 2πd ⎞
tanh ⎜
⎟
2π
⎝ L ⎠
4πd L ⎤
1⎡
Cg = nC = ⎢1 +
C
2 ⎣ sinh(4πd L)⎥⎦
E=
Energi gelombang
Perairan Dalam
d 1
<
L 2
C = Co =
L = Lo =
Cg =
L gT
=
T 2π
gT 2
= CoT
2π
1
gT
C=
2
4π
gH 2 L
8
Dimana : d = Kedalaman Perairan
L = Panjang Gelombang (m)
T = Periode Gelombang (detik)
C = Kecepatan Gelombang (m/detik)
g = Gravitasi (m/detik2)
Analisis Parameter Gelombang Pecah
Perhitungan
parameter
gelombang
pecah
perlu
diketahui
keadaan
kemiringan pantai pada segmen yang ditinjau sehingga indeks gelombang (γb)
pecah yang akan digunakan dalam perhitungan dapat ditentukan. Arah gelombang
datang tidak selalu tegak lurus dengan garis pantai, sehingga perlu
memperhitungkan pengaruh transformasi gelombang utama yakni pengaruh
refraksi dan shoaling (perubahan kedalaman). Penentuan besar sudut datang
gelombang di perairan dalam disesuaikan dengan sudut datang angin.
Analisis transformasi gelombang, dapat dilakukan dengan menentukan
gelombang dalam ekivalen ( H o' ) dengan menggunakan persamaan (CHL, 2002):
H o' = H o K s K r
(1)
dimana Ks dan Kr adalah koefisien shoaling dan refraksi yang dihitung
dengan persamaan:
Ks =
C go
Cg
(2)
33
cos θ o
cos θ
Kr =
(3)
Indeks gelombang pecah dihitung dengan persamaan (Weggel 1972 dalam
CHL, 2002):
γb = b − a
Hb
gT 2
(4)
dimana a dan b merupakan fungsi kemiringan pantai tan β dan diberikan
oleh persamaan:
a = 43,75 (1 − e −19 tan β )
(5)
a = 43,75 (1 − e −19 tan β )
(6)
Komar dan Gaughan (1973) dalam CHL (2002) memperoleh hubungan
semi empiris indeks gelombang pecah (Ωb) untuk teori gelombang linear dengan
persamaan:
⎛ H' ⎞
Ωb = 0.56 ⎜ o ⎟
⎝ Lo ⎠
−1/ 5
(7)
Sehingga parameter gelombang pecahnya dapat dihitung:
Gelombang pecah:
H b = H o/ Ω b
(8)
Kedalaman gelombang pada saat pecah:
d b=
Hb
(9)
γb
Lebar daerah hempasan gelombang pecah:
Xb =
Hb
γ b tan β
(10)
Kecepatan grup gelombang pecah:
Cb = C gb = gd b
(11)
Tipe gelombang pecah:
⎛H
ξ o = tan β ⎜⎜ o
⎝ Lo
⎞
⎟⎟
⎠
−0.5
(12)
34
dimana ξo = surf similarity; tan β = kemiringan pantai; Ho dan Lo = tinggi
dan panjang gelombang di perairan dalam.
Selanjutnya tipe pecah dapat diduga berdasarkan surf similarity dengan
kriteria sebagai berikut:
Surging/Collapsing
ξo > 3,3
Plunging
0.5 < ξo < 3,3
Spilling
ξo < 0,5
Subskrib (o) menunjukkan sudut dan kecepatan gelombang sebelum pecah.
Perhitungan sudut datang gelombang pecah diperoleh dari hasil analisis
dengan menggunakan program RCPWave yang diinterpertasikan melalui hasil
peta transformasi gelombang pada setiap arah dan profil pantai yang ditinjau.
Analisis Transformasi Gelombang Menggunakan Model RCPWave
Selain hasil analisis dengan menggunakan persamaan empiris di atas,
penelitian ini juga menggunakan model RCPWave sebagai solusi numerik dalam
penyelesaian proses transformasi gelombang yakni untuk proses refraksi dan
difraksi (Bruce et al. 1986). Model ini berisi suatu algoritma yang dapat
memperkirakan kondisi gelombang dalam surf zone, sehingga model gelombang
pecah dapat dibuat pada dua dimensi horizontal.
Berdasarkan bentuk pantai Eretan Kulon yakni pantai yang menghadap arah
utara, sehingga input data kedalaman pada program disesuaikan dengan hal
tersebut. Arah gelombang dari utara, barat laut dan timur laut dalam program
besar sudutnya masing-masing 0o, 45o dan -45o. Program ini dengan input data
gelombang maksimum, rata-rata dan minimum, sedangkan untuk yang hanya satu
karakteristik gelombang digunakan yang memiliki periode diatas 3 detik,
dikarenakan pada program ini hanya dapat mensimulasikan periode minimal 3
detik. Jumlah grid yang digunakan sebanyak [50,50], karena semakin banyak grid
yang dibuat maka akan semakin besar tingkat ketelitiannya. Output dari model
ini terdiri dari dua bagian (Lampiran 2), bagian pertama yaitu FNPRNT yang
berupa data hasil gelombang secara keseluruhan, terdiri dari data kedalaman,
sudut gelombang, tinggi gelombang, bilangan gelombang, dan indeks pecah
35
gelombang pada setiap grid, dan bagian kedua adalah savespec yang berupa data
muka gelombang dalam satu baris tertentu.
Aplikasi program ini dengan memasukkan model input data berupa tinggi,
periode, dan arah gelombang laut dalam (Ho, To, dan θo). Model input juga
memasukkan spesifikasi kontur kedalaman dasar pada grid (matriks). Variabel
sudut gelombang lokal, sudut gelombang air dalam dan sudut kontur kedalaman
dalam model ini didefinisikan pada Gambar 20.
Gambar 20. Definisi Sudut Dalam Model.
Keterangan : θo = Sudut gelombang laut dalam; θ = sudut gelombang lokal; θc = sudut
kontur daerah off-shore; di = kontur kedalaman ke-i, i = 1,2,3,... dst
Hasil tinggi gelombang pecah (Hb) yang diperoleh setiap grid dari model
akan dilihat dan ditest berdasarkan hasil perhitungan kedalaman gelombang pecah
(db) dari persamaan empirik Weggel (1976) dalam Bruce et al. (1986) dengan
syarat db ≥ d, yakni:
Hb =
bdb
ba
1+
gT 2
dimana a dan b dihitung berdasarkan persamaan (5) dan (6).
(13)
36
Hasil analisis dari RCPWave ini akan divisualisasikan melalui program
Surver dan ArcView untuk memudahkan dalam analisis deskriptif.
Longshore Current
Kecepatan arus menyusur pantai atau Longshore Current (v) akibat
pengaruh gelombang pecah dihitung dengan 3 persamaan empirik berikut, yakni:
1. Longshore current biasanya terjadi didaerah mid-surf dan bila berdasarkan
Longuet-Higgins (1970), maka didapat perbandingan antara longshore current
dan lebar surf-zone yang sangat kasar. Dengan menggabungkan data lapangan
di California oleh Putnam, Munk dan Traylor (1949); Saville (1950); dan
Brebner dan Kamphuis (1963) serta memperhitungkan teori gelombang linear
(Komar, 1979) maka didapat :
v = 1,17 gH b sin α b cos α b
(Komar dan Inman 1970 dalam Komar 1998)
2. Dilatar belakangi prediksi dari Longuet-Higgins (1970) yang diadaptasi dari
Bruun (1963) dan Galvin (1963) dengan menggunakan dua set data dari data
lapangan di California oleh Putnam, Munk dan Traylor (1949) dan data
laboratorium oleh Galvin dan Eagleson (1965) maka didapat modifikasi
persamaan empirik
v = 20,7 gH b tan β sin 2θ b
(CERC 1984).
3. Berdasarkan pembentukkan longshore current yang dibangkitkan oleh
gelombang (Longuet-Higgins (1970)) ditambah dengan asumsi bahwa
bathimetri dan tinggi gelombang homogen, memperhitungkan adanya
gelombang linear, sudut gelombang pecah yang kecil, kemiringan pantai yang
tidak sama, tidak adanya lateral mixing, dan gelombang pecah berada di surfzone. Faktor-faktor diatas menghasilkan persamaan empirik baru yaitu :
v=
5π tan β ∗
γ b gd b sin α b cos α b (CHL, 2002)
16 C f
tan β* = kemiringan pantai untuk wave setup =
tan β
⎛ ⎛ 3γ b2 ⎞ ⎞
⎜1 + ⎜
8 ⎟⎠ ⎟⎠
⎝ ⎝
37
⎛
⎛ Hb ⎞ ⎞
Cf adalah koefisien gesekan dasar = ⎜ 1, 742 + 2 Log10 ⎜
⎟⎟
⎝ 0, 001 ⎠ ⎠
⎝
−2
dimana: Hb = tinggi gelombang pecah; db = kedalaman gelombang pada saat
pecah αb = sudut gelombang pada saat pecah; tan β = m = kemiringan
pantai; γb = indeks gelombang pecah; g = percepatan gravitasi
(m/det2).