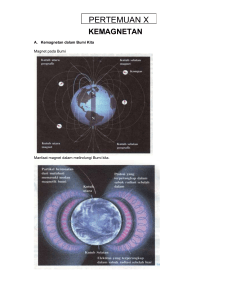
Medan Magnet

MAGNETIC FIELD
7/18/2017
IT TELKOM
MEDAN MAGNET
 Gejala kemagnetan mirip dengan apa yang terjadi pada
gejala kelistrikan
Misalnya :
 Suatu besi atau baja yang dapat ditarik oleh magnet
batangan
 Terjadinya pola garis-garis serbuk besi jika didekatkan
pada magnet batangan
 Interaksi yang terjadi pada peristiwa kemagnetan ini
adalah interaksi magnet yang nilai dan arahnya ditentukan oleh medan magnet.
7/18/2017
IT TELKOM
Medan Magnet
 Medan magnet merupakan medan vektor, artinya selain
memiliki besar medan juga memiliki arah
 Ada dua jenis sumber magnet yang menghasilkan medan
magnet
 Sumber Alamiah
Contohnya : Kutub Utara-Selatan Bumi
Magnet batangan
 Sumber Buatan
Sumber buatan ini dapat dibuat dengan mengalirkan
arus listrik pada suatu lilitan kawat
7/18/2017
IT TELKOM
Medan Magnet
 Tahun 1820 Oersted menemukan bahwa arus listrik
yang mengalir pada sebuah penghantar dapat menghasilkan efek-efek magnetik
 Fenomena ini dapat ditunjukkan dengan melihat adanya
penyimpangan arah jarum kompas bila didekatkan pada
penghantar berarus
i
Sebelum ada
arus
7/18/2017
Setelah kawat dialiri arus i, arah
Jarum kompas lebih menyimpang
Daripada sebelum dialiri arus
Setelah ada
arus i
IT TELKOM
Arah Medan Magnet
 Arah medan magnet akibat arus listrik dapat ditentukan
dengan menggunakan aturan tangan kanan
I
B
I B
Arah I ditunjukkan dengan arah ibu jari
Sedangkan arah perputaran keempat
Jari lainnya menunjukkan arah medan
Magnet yang dihasilkan
 Arah medan magnet di sekitar magnet batangan berarah
dari utara menuju selatan
7/18/2017
IT TELKOM
7/18/2017
IT TELKOM
Hukum Biot-Savart
 Hukum Biot-Savart dinyatakan oleh Jeans Baptiste Biot
(1774-1862) dan Felix Savart (1791-1841) sesaat setelah
Oersted menemukan fenomena arus listrik dapat menghasilkan medan magnet
 Hukum Biot-Savart digunakan untuk menghitung medan
magnet yang ditimbulkan oleh arus listrik
P
Tinjau suatu kawat yang panjangnya L dan dialiri arus I
Bagaimana menentukan medan
magnet di titik P ?
I
7/18/2017
IT TELKOM
Hukum Biot-Savart

r

dl
dB
x
P
Menurut Biot dan Savart, arus I yang
mengalir pada kawat ditinjau sebagai
banyak elemen kecil arus yang mengalir pada elemen kecil kawat dl
r̂
I
Hukum Biot-Savart menyatakan elemen kecil medan magnet
yang timbul di titik P akibat elemen kecil arus Idl adalah

  0 I dl xrˆ
dB 
,
2
4 r

r̂
r adalah
 vektor perpindahan dari dl ke P, dan adalah vektor
dengan
satuan searah
7/18/2017
r
IT TELKOM
Hukum Biot-Savart
Arah medan magnet di P dapat ditentukan dengan aturan
tangan kanan, yaitu masuk bidang gambar
Sedangkan Besar elemen kecil medan magnet dB di titik P
tersebut adalah
 i dl sin 
dB  0
4 r 2
dengan  adalah sudut antara dl dan vektor r
Besar medan magnet di titik P akibat seluruh panjang kawat
yang berarus I tersebut adalah



 0i dl xrˆ
B   dB  
.
2
4 r
7/18/2017
IT TELKOM
Kawat Lurus berarus
Tinjau sebuah kawat lurus sangat panjang dialiri arus listrik I
seperti pada gambar di bawah.
P
a
I
Kita akan coba menerapkan hukum Biot-Savart untuk menentukan medan magnet pada jarak a dari pusat simetri
kawat.
Anggap jarak a jauh lebih kecil dari panjang kawat atau kita
pandang kawat panjangnya tak berhingga
7/18/2017
IT TELKOM
Kawat Lurus berarus (2)
Langkah-langkah Penyelesaian :
 Buat sumbu-sumbu koordinat untuk membantu dalam perhitungan, yaitu sumbu x ke kanan dan sumbu y ke atas,
dengan pusat koordinat (O) tepat di bawah titik P
Pada sumbu koordinat x, kawat terbentang dari - sampai +
y
P
r
I dlI
-
a

+
dl
x
 Kawat berarus dianggap tersusun atas elemen kecil dl, dengan
arah ke kanan (searah I). Karena dl searah sb x maka dl=dx
7/18/2017
IT TELKOM
Kawat Lurus berarus (3)
 Arah medan magnet adalah keluar bidang gambar
 Besar Elemen kecil medan magnet dB akibat elemen kecil
kawat dl berarus I adalah
0 I dl sin  0 I dx sin 
dB 

2
4
r
4 x 2  a 2 
dengan variabel  dan variabel x tidak saling bebas
 Besar medan magnet total di titk P adalah

 0i dx sin 
B 
2
2


4

x

a

Integral di atas dapat dipermudah dengan mengganti
variabel  dengan  dimana sin=cos
7/18/2017
IT TELKOM
Kawat Lurus berarus (4)
 Hubungan x dengan 
x  a tan   dx  a sec 2 d

 0i dx sin 
B 
2
2


4

x

a


 0i
cos d

4a

 Jika x   maka    sehingga besar medan magnet
2
di titik P adalah


 
 0i 2
 0i
2
B
cos

d


sin


 
4a 
4a
2

 0i 2
B
Tesla
2a
7/18/2017
IT TELKOM
Kawat Lurus berarus (5)
Bagaimana jika panjang kawatnya berhingga katakanlah
Sama dengan L ?
P
a
I
L
Pada prinsipnya penyelesaian kasus medan magnet akibat
kawat lurus berarus I yang panjangnya berhingga ini sama
ngan kasus kawat tak berhingga
Bedanya adalah batas sepanjang sumbu x dari x=-L/2
sampai dengan x=+L/2
7/18/2017
IT TELKOM
Kawat Lurus berarus (6)
y
P
r
I dlI
-L/2
a

+L/2
dl
x
 Besar Elemen kecil medan magnet dB akibat elemen kecil
kawat dl berarus I adalah
dB 
0 I dl sin  0 I dx sin 

2
4
r
4 x 2  a 2 
 Besar medan magnet total di titk P adalah
L/2
B
7/18/2017
0i dx sin 
2
2



4

x

a
L / 2
IT TELKOM
Kawat Lurus berarus (7)
 Hubungan x dengan 
x  a tan   dx  a sec 2 d
 Besar medan magnet di P menjadi
 0 I dx sin   0 I cos d
B 

2
2
4

a
4 x  a 


0 I
0 I 
x

sin   
B
4a
4a  x 2  a 2
0 I 
L

B
2a  L2  4a 2
7/18/2017

 Tesla


IT TELKOM
x L / 2



 x L / 2
Contoh
Suatu kawat lurus yang panjangnya 4 m dibentangkan dari
x=-4 m sampai x=0. Kawat dialiri arus 2 A. Tentukan medan
magnet di titik (0 m,3m).
y
P
3m
I=2A
x
-4
4m
7/18/2017
IT TELKOM
Untuk kasus ini elemen kecil dl berjalan dari x=-4 m sampai
y
dengan x=0 m.
P
r
I=2A
-4
3m

x
dl
4m
 Arah medan magnet adalah keluar bidang gambar
 Elemen kecil dl searah dengan sumbu x, dl=dx dan berjalan dari -4 m sampai 0.
7/18/2017
IT TELKOM
 Besar elemen kecil medan magnet di titik P adalah
0 I dl sin  0 (2) dx sin  0 dx sin 
dB 


2
2
2
4
r
4 x  3  2 x 2  9
 Besar medan magnet total di titk P adalah
2
0
x

3
tan


dx

3
sec
d
 0 dx sin 
B 
, gunakan x  0    0
2
2 x  9 
4
x  4    53o
0
0

cos d

2 (3) 53

7/18/2017
0
sin   053  0 4  40 T
6
6 5 30
IT TELKOM
Kawat Lingkaran berarus
Tinjau sebuah kawat lingkaran dengan jari-jari R dialiri arus
listrik I seperti pada gambar di bawah.
z
Kawat lingkaran terletak
pada bidang xz
I
P
R
y
a
x
Kita akan coba menerapkan hukum Biot-Savart untuk
menentukan medan magnet pada jarak a dari pusat
Kawat lingkaran
7/18/2017
IT TELKOM
7/18/2017
IT TELKOM
Kawat Lingkaran berarus (2)
Langkah – langkah Penyelesaian :
 Buat elemen kecil panjang
(keliling) lingkaran dl dengan
arah sama seperti arah arus I
z
Idl

r
P
R
a

x
7/18/2017
dB
dl
dBy
y
dB
 Uraikan/gambarkan arah-arah
medan magnet dB di titik P
akibat elemen kecil Idl
IT TELKOM
Kawat Lingkaran berarus (3)
 Komponen medan magnet dalam arah sumbu z akan
saling meniadakan (Bz=0)
 Komponen medan magnet dalam arah sumbu x juga
saling meniadakan (By=0)
 Jadi hanya ada komponen medan magnet dalam arah
sumbu y
 Besar elemen kecil medan magnet dB adalah
 I dl sin  0 I
dl
dB  0

4
r2
4 ( R 2  a 2 )
Ingat  adalah sudut antara arah Idl dengan r, dalam kasus ini
=90o (arah Idl tegak lurus dengan arah r)
 Besar elemen kecil medan magnet dB dalam arah sb y:
dBY  dB cos  
7/18/2017
0 I dl
0 I
dl
R
cos


4 R 2
4 R 2  a 2  R 2  a 2
IT TELKOM
Kawat Lingkaran berarus (4)
 Besar elemen kecil medan magnet dalam arah sumbu y
adalah
2R
0 I 2R
0 I
0 I
Rdl
R
R2
BY 

dl 
3/ 2
3/ 2 

2
2
2
2
4 0 R  a 
4 R  a  0
2 R 2  a 2 3 / 2
Batas atas integral diambil sama dengan satu keliling lingkaran
karena panjang total kawat adalah satu keliling lingkaran dan
Jari-jari lingkaran R serta jarak a adalah konstan sehingga dapat
dikeluarkan dari integral
 Jadi medan magnet di titik P akibat kawat lingkaran tersebut adalah
 0 I
R2
B
2 R2  a2

7/18/2017

3/ 2
ˆj Tesla
IT TELKOM
Kawat Lingkaran berarus (5)
Bagaimana jika titik P dalam kasus kawat lingkaran berarus I
di atas terletak di pusat lingkaran ?
y
 Arah medan magnet adalah
masuk bidang gambar
I
dl
P
R x dB
x
 Kawat lingkaran dianggap
tersusun atas elemen kecil
panjang dl
Besar medan magnet akibat elemen kecil Idl adalah
dB 
7/18/2017
0 I dl sin  0 I dl

2
4
r
4 R 2
IT TELKOM
Kawat Lingkaran berarus (6)
Elemen kecil panjang dl berjalan dari nol sampai satu
keliling lingkaran sehingga batas integral dalam menghitung
Medan magnet total adalah dari 0 sampai 2πR
Besar medan magnet total di P adalah
0 I
B 
4
7/18/2017
2R

0
0 I
dl

2
R
4R 2
2R
0 I
 dl  2R
0
IT TELKOM
Contoh
Sebuah kawat ¾ lingkaran memiliki jari-jari 2 m dan dialiri
arus 4 A. Berapakah medan magnet di pusat kawat tsb?
 Arah medan magnet adalah
masuk bidang gambar
y
Besar medan magnet akibat
elemen kecil Idl adalah
I
P
R
x
dB 
 0 I dl sin   0 4 dl 0


dl
2
2
4
r
4 2
4
Elemen kecil panjang dl berjalan dari nol
sampai 3/4 keliling lingkaran sehingga batas
integral dalam menghitung medan magnet
total adalah dari 0 sampai 3πR/2=3π
7/18/2017
IT TELKOM
Besar medan magnet total di P adalah
0 3
30
B 
dl 
T

4 0
4
7/18/2017
IT TELKOM
SOAL
I1
Dua buah kawat yang masing-masing sangat
panjang, kawat pertama diberi arus I1=2 A,
kawat kedua diberi arus I2=3 A. Hitung
Medan magnet B (oleh kawat pertama) di titik
yang jaraknya d dari kawat pertama.
I2
d=20 cm
P
R
Q
a
I
S
L
L/4
7/18/2017
L/4
Kawat lurus (cetak tebal) yang
panjangnya L dialiri arus I.
Dengan menggunakan hukum
Biot-Savart, tentukanlah medan
magnet yang terjadi di titik
P, Q, R, dan S.
IT TELKOM
SOAL
R
P
I
a
3R
R
P
I
7/18/2017
Sebuah loop berbentuk lingkaran berjari
jari R dialiri arus listrik I. Dengan menggunakan hukum BiotSavart, tentukanlah :
a. Medan magnet di titik P.
b. Medan magnet di pusat lingkaran loop.
Suatu sistem terdiri atas kawat ¾ lingkaran dihubungkan dengan dua kawat
lurus sejajar seperti gambar. Jika pada
sistem mengalir arus I seperti gambar,
tentukanlah medan magnet di titik P
(pusat lingkaran).
IT TELKOM