IV. Arus Listrik

IV. Arus Listrik
Sebelum tahun 1800:
listrik buatan hanya berasal dari friksi (muatan statis)
== tidak ada kegunaan praktis
listrik alam Æ kilat
Pada tahun 1800:
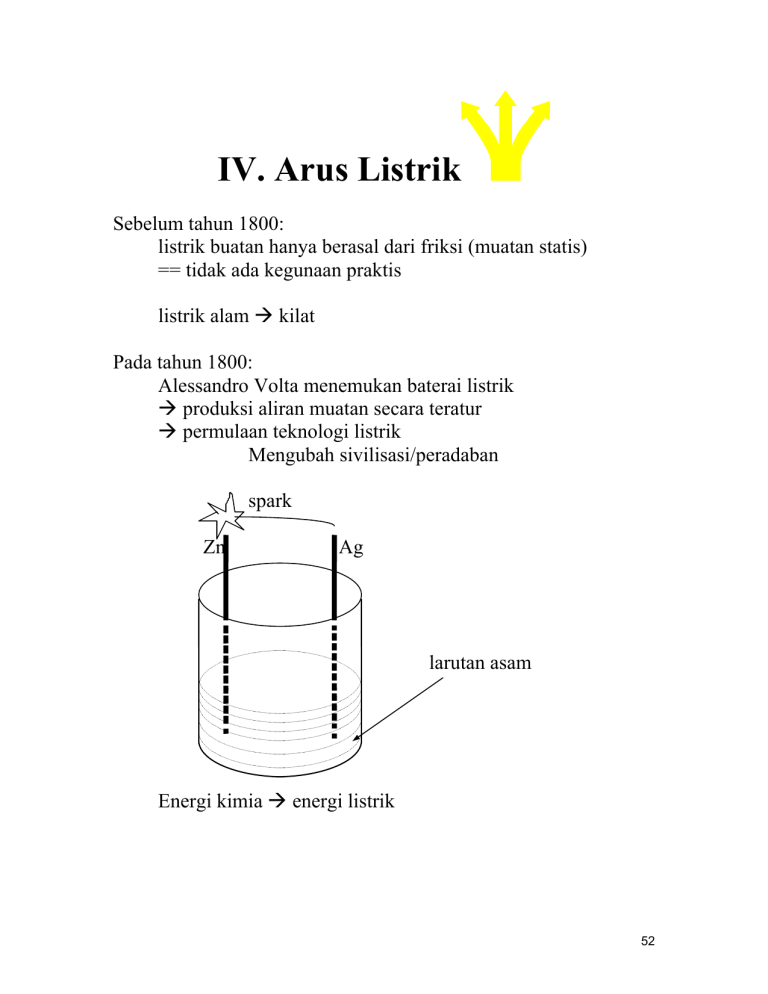
Alessandro Volta menemukan baterai listrik
Æ produksi aliran muatan secara teratur
Æ permulaan teknologi listrik
Mengubah sivilisasi/peradaban
spark
Zn
Ag
larutan asam
Energi kimia Æ energi listrik
52
Baterai modern
* baterai kering
* accu
* sel
Kenapa ada arus listrik?
+
-
Carbon
Zn
Katode
Anoda
larutan elektrolit
Ada beda potensial antara kedua elektroda
Æ terjadi elektromotive force (emf) atau gaya gerak listrik (ggl)
Æ tegangan baterai (ε)
Penyederhaan penggambaran:
+
-
6 volt
53
Di dalam kawat:
arus
e-
e-
e-
ee-
arus listrik/I:
ΔQ
I=
Δt
ee-
e-
e-
muatan per satuan waktu
Pada t tertentu:
dQ
satuan Ampere = Coulomb/detik
I=
dt
Hukum Ohm
arus
I
V
Dapat dipahami bahwa arus listrik yang terjadi (I) Æ proporsional
dengan tegangan yang diberikan (V)
I ∝V
Atau lebih eksplisit:
V
I=
R
konstanta tergantung jenis & geometri
R disebut resistan atau tahanan
54
V=IR
Hukum Ohm ini berlaku untuk logam/konduktor
Tetapi tidak berlaku umum
Tidak berlaku pada semikonduktor, transistor dan material non
linear.
Satuan R : Ohm (Ω)
1 Ω = 1 volt/ampere
Simbol:
Contoh soal:
Pada sebuah tape recorder kecil tertulis apabila dihubungkan
dengan 6 volt akan menghasilkan arus 300 mA
(a) Berapa net resistan dari tape?
(b) Bila potensial turun menjadi 5 volt, bagaimana perubahan arus
listrik?
Jawab:
(a) V = 6 volt dan I = 300 mA = 0,3 A
V = I R Æ R = (6)/(0,3) = 20 Ω
(b) Kalau resistan tetap konstan
V
= 5,0/20 = 0,25 A
Arus: I =
R
sebenarnya resistan bergantung pada temperatur
55
Resistivitas dan Konduktivitas
Arus listrik /I
Area/A
Panjang/L
Tahanan/resistan: R
L
R=ρ
A
disini ρ adalah konstanta yang bergantung ada jenis material dan
juga:
„ kemurnian
„ proses pembuatan
„ temperatur
ρ disebut sebagai tahanan jenis (resistivitas)
Satuan: Ω m
Bahan
perak
tembaga
Al
besi
ρ (Ω m)
1,59x10-8
1,68x10-8
2,65x10-8
9,71x10-8
Kebalikan resistivitas Æ konduktivitas/ σ = 1/ρ
[kemampuan suatu bahan untuk
menghantarkan arus listrik]
56
Contoh soal:
Sebuah kawat tembaga (ρ =1,68x10-8 Ωm) akan digunakan untuk
menghubungkan sebuah radio dan speaker luar. Panjang kawat 20
meter. Berapa diameter kawat supaya resistan/tahanan kurang dari
0,1 Ω.
Jawab:
L
maka semakin besar luas, tahanan akan mengecil.
A
Oleh karena itu yang akan dihitung adalah diameter maksimal.
Karena R = ρ
Æ luas penampang A = ρ L/R = (1,68x10-8)(20)/0,1=3,4x10-6 m2
A = π r2
Sehingga r =1,05x10-3 m
diameter = 2 r = 2,1 x10-3 m = 2,1 mm
Pengaruh Temperatur pada Resistan
Besar resistivitas bervariasi terhadap temperatur, hal ini dapat
diterangkan dengan teori zat padat, khususnya tentang ikatan atom.
Pada konduktor:
Temperatur naik Æ resistivitas naik
e-
Elektron tidak terikat kuat, sehingga ketika suhu naik Æ
atom-atom akan bervibrasi dengan lebih cepat Æ
menghalangi gerakan elektron Æ tahanan naik
57
Pada semikonduktor
Elektron terikat lebih kuat.
Ketika suhu dinaikkan
Æ elektron menjadi lebih tidak terikat dan dapat bergerak
lebih mudah
Æ menaikkan konduktivitas
Æ resistivitas turun
Kembali ke konduktor, biasanya digunakan pendekatan linear:
ρT = ρo {1 + α (T - To)}
koefisien temperatur
resistivitas pada suhu To
resistivitas pada suhu T
Daya Listrik
Mengapa kita memilih bentuk energi listrik?
Æ karena mudah ditransformasi dalam bentuk-bentuk energi lain
Alat-alat rumah tangga:
* tungku listrik
* toaster
energi listrik Æ panas
* lampu
energi listrik Æ panas + cahaya
58
Proses fisis transformasi energi:
I
eee-
I
pada resistan (dalam hal ini pada alat listrik rumah tangga)
Æ terjadi tumbukan antara elektron-elektron dan material
Æ timbul panas
Kerja dU = dq V
Energi persatuan waktu (laju energi):
dU dq
=
V = IV
P=
dt
dt
Daya listrik:
P = I V atau I2 R atau V2/R
satuan daya Æ joule/detik = watt
Para pelanggan PLN membayar energi (dalam joule) bukan daya.
Satuan lebih besar 1 kwh = kilo watt jam
Jadi
1 kwh = 1000 watt x 3600 detik
= 3,6x106 watt detik
= 3,6 x106 joule
59
Contoh soal:
Sebuah tungku listrik menghasilkan arus 4 A untuk tegangan 220
volt. Berapa tarif PLN yang harus dibayar per-bulan (30 hari) bila
secara rata-rata tungku tersebut digunakan 3 jam per-hari.
1 kwh = Rp. 115,Jawab:
Daya: P = I V = (4)(220) = 0,88 kW
Tungku tersebut bekerja selama 30x3 = 90 jam
Jadi membutuhkan biaya: 0,88x90xRp. 115 = Rp. 9108,-
Rangkaian Resistor
Rangkaian seri
R1
Dapat dibuktikan:
R2
R3
R = R1 + R2 + R3
R = Σ Ri
Rangkaian paralel
R1
R2
1
1
1
1
=
+
+
R R1 R 2 R 3
R3
60
Contoh soal:
400 Ω
a
500 Ω
I1
b
700 Ω
c
I
I2
ε =12 volt
Hitung arus listrik yang mengalir pada tahanan 500 Ω !
Jawab:
Kita lihat rangkaian equivalen:
400 Ω
a
b
290 Ω
c
I2
I
ε =12 volt
Sebagai tahanan pengganti tahanan 500 Ω dan 700 Ω:
1
1
1
=
+
Æ R = 290 Ω
R 500 700
Sehingga tahanan equivalen keseluruhannya:
RT = 400 Ω + 290 Ω = 690 Ω
61
Sehingga arus yang mengalir melalui titik a:
I = V/RT = 12/690 = 0,017 A
Vac = Va - Vc = 12 volt
Æ Vab = I Rab = (0,017)(400) = 6,8 volt
Oleh karena itu tegangan yang melalui tahanan 500 Ω adalah
Æ Vbc = Vac - Vab = 12 - 6,8 = 5,2 volt
Sehingga arus yang melalui tahanan 500 Ω adalah:
I = V/R = (5,2)/(500) = 0,01 A = 10 mA
Tahanan Dalam (Internal Resistance)
Sebagaimana yang disebutkan sebelumnya, baterai, generator
listrik dan tipe sumber lain mengubah satu jenis energi (kimia,
mekanik, cahaya dll.) menjadi energi listrik.
Æ hal ini disebut sebagai sumber ggl (gaya gerak listrik)
Penamaan “gaya” gerak listrik sebenarnya salah kaprah, karena
yang kita maksud bukan “gaya” (bersatuan Newton) tetapi suatu
potensial listrik.
Kita amati bahwa potensial (ggl) sebuah baterai makin lama makin
turun dan akhirnya mati (nol)
Æ hal ini karena ada tahanan dalam (internal resistance) pada
baterai
Æ pada proses yang berlangsung (misal ada proses kimia) nilai
tahanan dalam akan naik
Æ tegangan baterai turun.
62
Kondisi sesungguhnya:
a
b
r
ε
disini r merupakan tahanan dalam
Vab = ε - I r
Terlihat nilai tegangan Vab (“tegangan jepit”) lebih kecil dari ggl (ε).
63
Hukum Kirchhoff
I. Hukum Sambungan/ Kirchhoff I
“pada suatu titik sambung, jumlah arus yang masuk sama
dengan jumlah arus yang keluar”
I2
I1
I3
I4
I 1 = I2 + I3 + I4
(hukum ini sebenarnya merupakan perluasan hukum kekekalan
muatan)
64
II. Hukum Rangkaian / Hukum Kirchhoff II
“Pada suatu rangkaian tertutup, jumlah aljabar perubahan
potensial adalah nol”
Contoh:
a
I
b
R1
I
R2
d
c
ε
loop/rangkaian abcd:
Æ Vaa = 0
Tinjau masing-masing beda potensial:
(sebab potensial di a > dari di b)
Vba = Vb - Va = - I R1
Vcb = Vc - Vb = - I R2
Vdc = + ε
Vad = 0
(sebab Va = Vd)
Sehingga menurut hukum Kirchhoff II:
Vba + Vcb + Vdc + Vad = 0
- I R2 - I R1 + ε = 0
atau ε = I (R1 + R2)
suatu formula yang sudah kita kenal
Gunakan logika berpikir, jangan menghapal rumus!!!
65
Penerapan hukum Kirchoff I & II untuk kasus yang lebih
kompleks:
Pada rangkaian di bawah ini, hitung arus I1, I2 dan I3 (arus setiap
percabangan)!
30 Ω
a
b
I3
d
I1
c
40 Ω
45 V
f
r=1Ω
I2
20 Ω
1Ω
80 V
g
e
h
i
Jawab:
Kita gunakan hukum Kirchhoff I:
Pada titik cabang c:
(1)
I3 = I1 + I2
Lalu hukum Kirchoff II kita terapkan pada:
(a) loop abfedca
Vba + Vfb + Vef + Vde + Vcd + Vac = 0
-30I1+ 0 + 45 - I3 - 40I3 + 0 = 0
Æ 30 I1+ 41 I3 = 45
(2)
66
(b) loop cdefihgc
Vdc + Ved + Vfe + Vif + Vhi + Vgh + Vcg = 0
40I3 + I3 - 45 + 20 I2 + I2 - 80 + 0 = 0
Æ 41 I3 + 21 I2 = 125
(3)
Gabung persamaan (1), (2) dan (3) didapat:
I1 = - 0,87 A
(jadi arah arus sesungguhnya berlawanan
dengan yang diasumsikan)
I2 = 2,6 A
I3 = 1,7 A
Contoh lain:
I
a
b
I2
I1
R
ε
R
I3
c
R
d
R
I4
f
R
I
I5
e
ε = 12 voltdan R (semua sama) = 2 Ω
Hitung arus yang mengalir di semua cabang!
Jawab:
67
Lihat loop cdb:
- I 3 R - I 2 R + I1 R = 0
Æ - I3 - I2 + I1 = 0
(1)
Lihat loop edc
Æ - I5 + I 3 + I 4 = 0
(2)
(1) + (2)
Æ - I2 + I1 - I5 + I4 = 0
Æ - I5 + I4 = I2 - I1 (I)
Hukum Kirchhoff I mendiktekan:
(3)
I4 = I3 + I1
(4)
I5 = I2 - I3
(3) + (4)
Æ I4 + I 5 = I 1 + I 2
(II)
(I) + (II) Æ I4 = I2
(I) - (II) Æ I5 = I1
(3)- (4) Æ I4 - I5 = I1 - I2 + 2I3
terus
I4 - I5 = I5 - I4 + 2I3 Æ I3 = I4 - I5
bandingkan dengan (2) Æ I3 = I5 - I4
Æ hanya mungkin bila I3 = 0
lihat kembali (3) & (4) Æ I4 = I1 dan I5 = I2
Terjadi kesamaan Æ I1 = I2 = I4 = I5 = ½ I
Kembali ke kaidah baterai: ε = I1R + I4R = 2 I1 R = 12 volt
Æ I1 = 3 ampere dan juga arus cabang lain.
Alat-alat Ukur Listrik
68
Pengukur beda tegangan
Æ voltmeter
V
Pengukur arus listrik
Æ ammeter
A
Î Bagian pokok kedua alat ini Æ galvanometer
(pengukur arus kecil)
Galvanometer dapat bekerja karena ada gaya antara medan magnet
dan arus listrik pada kawat koil (akan didiskusikan dalam bab
Medan Magnet)
Magnet Permanen
U
S
Arus listrik order 50 μA
Simbol Galvanometer:
G
Galvanometer dapat langsung digunakan untuk mengukur arus
listrik yang kecil.
Untuk arus listrik:
G
r
IG
I
I
R
69
A
=
IR
Untuk Tegangan
R
V
=
r
G
Ammeter
Untuk mengukur arus yang lebih besar, disini galvanometer
ditambah suatu resistor shunt.
Misal untuk mengukur arus maksimum 1 A dengan galvanometer
berskala maks 50 μA dan resistan r = 30 Ohm, hitung tahanan
shunt yang dibutuhkan?
G
r
IG
I
R
IR
I = 1 ampere
IG = 50 μA = 0,00005 ampere, sehingga IR = 0,99995 ampere
Æ lihat beda tegangan:
IG r = IR R Æ (0,00005)(30) = (0,99995) R Æ R = 0,0015 Ohm
Voltmeter:
70
Hitung tahanan paralel yang dibutuhkan sebuah galvanometer
(arus 50 μA, r = 30 Ohm) untuk mengukur beda potensial antara 015 volt.
Jawab:
V = I (R + r)
15 = (0,00005)(R + 30) Æ R sekitar 300 kΩ
(sangat besar)
71