B A B II

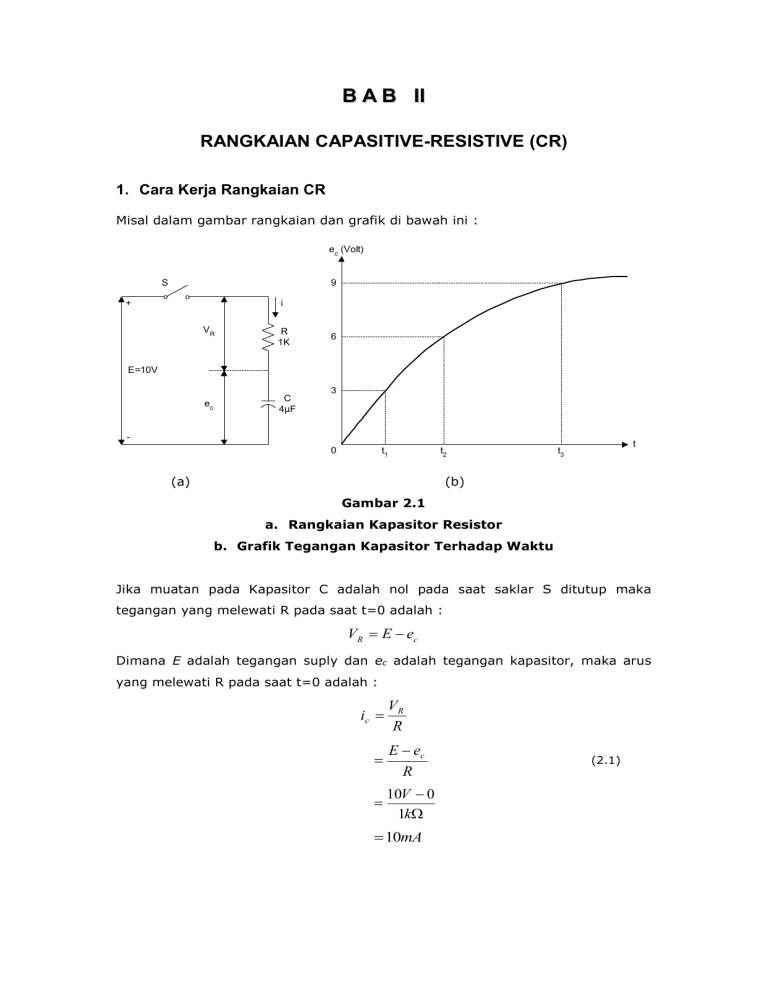
B A B II
RANGKAIAN CAPASITIVE-RESISTIVE (CR)
1. Cara Kerja Rangkaian CR
Misal dalam gambar rangkaian dan grafik di bawah ini :
ec (Volt)
S
9
+
i
VR
R
1K
6
E=10V
3
ec
C
4µF
0
t1
t2
(a)
t
t3
(b)
Gambar 2.1
a. Rangkaian Kapasitor Resistor
b. Grafik Tegangan Kapasitor Terhadap Waktu
Jika muatan pada Kapasitor C adalah nol pada saat saklar S ditutup maka
tegangan yang melewati R pada saat t=0 adalah :
VR  E  ec
Dimana E adalah tegangan suply dan ec adalah tegangan kapasitor, maka arus
yang melewati R pada saat t=0 adalah :
ic 
VR
R

E  ec
R

10V  0
1k
 10mA
(2.1)
Arus ini menyebabkan kapasitor C dimuati (charge) dengan polaritas seperti pada
gambar 2.1.b, sehingga pada saat t1 tegangan ec menjadi 3 volt. Hal ini
mengubah harga VR menjadi :
VR  E  ec
 10V  3V  7V
ic  (10V  3V ) / 1k  7mA
harga IC berubah menjadi :
Karena C terus dimuati, maka ec terus bertambah dan tegangan VR berkurang,
jadi arus yang melewati R juga berkurang. Karena arus berkurang maka C
dimuati lebih lambat dari sebelumnya. Beberapa saat selanjutnya e c bertambah
menjadi 6 Volt (t2 pada grafik), maka harga VR menjadi :
VR  10V  6V  4V
ic 
dan
4V
 4mA
1k
Arus pengisian sekarang semakin berkurang lebih banyak lagi sehingga untuk
pengisian C sebesar 3 Volt berikutnya dibutuhkan waktu yang semakin lama.
Pengisian tegangan C tidak berlangsung tetap, yaitu bahwa ec akan semakin
meningkat dan tegangan R akan terus menurun, begitu juga arus yang mengalir
semakin berkurang. Hal ini berarti bahwa pengisian capacitor sangat cepat (arus
besar) pada awal pengisian kemudian akan terus berkurang seiring dengan
naiknya tegangan capacitor.
Terlihat arus terus berkurang. Tegangan yang ada pada kapasitor diberikan
seperti pada rumus exponensial berikut :
t
CR
ec  E  ( E  E0 ) 
dimana :
ec
= tegangan kapasitor
E
= tegangan sumber/pengisian
E0
= tegangan awal pada kapasitor

= konstanta eksponensial = 2,718
t
= waktu pengisian
C
= kapasitor yang dimuati
R
= hambatan pengisian
Jika tidak ada muatan awal pada C maka :
E0  0
t
ec  E  ( E  0) CR
atau
(2.2)
t
CR
ec  E (1  )
(2.3)
kemudian,
ic 
E  ec
R
t
E  E (1 CR )
ic 
R
maka,
t
E
ic  CR
R
dan
t
ic  I CR
(2.4)
dimana I=E/R adalah arus awal saat t=0.
CONTOH 1
Hitung level tegangan eC, pada rangkaian Gambar 1, pada saat interval 2 ms
setelah switch S ditutup. Gambarkan grafik eC terhadap waktu.
Penyelesaian
Pada saat Eo=0 maka :
t = 0 ms

ec  E (1 0 )
t = 2 ms

ec  10(1 41 )
t = 4 ms

ec  10(1 41 )
= 0 volt
… point 1
= 3,93 volt
… point 2
= 6,32 volt
… point 3
2
4
dengan cara yang sama :
t = 6 ms

eC
= 7,7 volt
… point 4
t = 8 ms

eC
= 8,65 volt
… point 5
t = 10 ms

eC
= 9,18 volt
… point 6
t = 12 ms

eC
= 9,50 volt
… point 7
t = 14 ms

eC
= 9,70 volt
… point 8
t = 16 ms

eC
= 9,82 volt
… point 9
CONTOH 2
Tentukan arus pengisian dalam rangkaian gambar 1.a pada interval waktu 2 ms
saat setelah switch S ditutup. Gambarkan grafiknya i C terhadap waktu.
Penyelesaian
Dengan menggunakan persamaan
iC  ( E  eC ) / R
(2.4)
Pada saat t = 0 …. ec lihat hasil contoh 1.
t = 0 ms
 ic 
(10  0)
1K
= 10 mA
… point 1
t = 2 ms
 ic 
(10  3,93)
1K
= 6,07 mA
… point 1
t = 4 ms
 ic 
(10  6,32)
1K
= 3,68 mA
… point 1
dengan cara yang sama :
t = 6 ms

iC
= 2,23 mA
… point 4
t = 8 ms

iC
= 1,35 mA
… point 5
t = 10 ms

iC
= 0,82 mA
… point 6
t = 12 ms

iC
= 0,50 mA
… point 7
t = 14 ms

iC
= 0,30 mA
… point 8
t = 16 ms

iC
= 0,18 mA
… point 9
12
1
10
5
8
7
8
9
4
6
4
Ic(mA) ec(V)
6
2
3
2
3
ec=Tegangan Kapasitor
ic=Arus Pengisian
4
2
5
1
0
0
2
4
6
8
6
10
7
12
8
14
9
16
t (ms)
Gambar 2.2 Grafik Tegangan dan Arus Kapasitor terhadap waktu
Dengan melihat gambar diatas maka kapasitor akan terus dimuati sampai level
tegangan suply. Misalnya sekarang tegangan input menjadi nol, sedang switch S
closed, maka hasilnya adalah kapasitor akan discharge (pengosongan) melalui R.
dari persamaan 2-2 dapat digunakan untuk menghitung tegangan kapasitor
setiap saat selama masa discharge. Jika pada saat discharge muatan kapasitor
adalah E (misal level muatan sebelum E adalah 0). Maka selama E menjadi nol,
karena itu persamaan 2-2 dapat disederhanakan menjadi :
t
CR
ec  0  (0  E ) 
t
ec  E CR
(2.5)
Jika kurva discharge kapasitor digambar (dengan persamaan 2-5) akan didapat
seperti pada gambar 2.1.
Pada gambar 2.3 diperlihatkan kurva normalisasi charge dan discharge. Kurva ini
dapat dipakai untuk menyelesaikan soal grafik. Kurva normalisasi digambar pada
kondisi E=1 Volt, C=1 F dan R=1 . Untuk harga harga ini tegangankapasitor
dapat ditentukan pada waktu t yang diberikan setelah permulaan charge dan
discharge.
1
0,8
a
Charge
0,6
0,4
Discharge
ec(V)
0,2
b
0
0
1
2
3
4
5
t (CR seconds)
Gambar 2.3 Kurva Normalisasi Charge dan Discharge Untuk
Rangkaian CR
Jika E tidak sama dengan 1 Volt, tegangan kapasitor pada waktu yang diberikan
dapat ditentukan dengan mengalikan tegangan dari kurva dengan harga E. Misal
jika e=5 Volt dan t=0,75 s pada kurva,
maka :
ec  0,5V  5V  2,5V
Dengan cara yang sama jika C dan R dengan harga lain dari 1 F dan 1 , maka
waktu setiap saat ditentukan dengan mengalikan CxR. Misal C=1 µF dan R=1 k.
Jika ec=0,5 Volt, maka waktu untuk mencapai 0,5 Volt adalah :
t  0,7 s  1µF  1K
t  0,7ms
CONTOH 3
Gunakan grafik normalisasi charge dan discharge, tentukan :
a. ec pada 1,5 ms dimulai dari ec=0 Volt, jika R=1 k, C=1 µF dan E=10 Volt.
b. ec pada 6 ms dari muatan penuh jika R=20 k, C=1 µF dan E=12 Volt.
Penyelesaian
a. Masing-masing waktu di skala menjadi
1s x 1 µF x 1 KΩ = 1 ms
saat t=1,5 ms (titik a gb. 2.3 grafik charge)
ec
= 10V x 0,78
= 7,8 V
b. Masing-masing waktu di skala menjadi
1s x 0,1 µF x 20 KΩ = 2 ms
saat t=6 ms (titik b gb. 2.3 grafik discharge)
ec
= 12V x 0,05
= 0,6 V
2. Persamaan Rangkaian CR
Gambar 2.4 Hubungan antara CR dan T terhadap Arus dan Tegangan
Capacitor
Gambar 2.4 adalah arus charging dan tegangan kapasitor di gambar terhadap
waktu, seperti pada rangkaian gambar 2.1 terlihat bahwa jika t=4 ms, e c=6,32 V.
Dalam kasus ini 4 ms adalah perkalian dari :
t  C  R  4 µF  1K  4 
1
= 4 ms
1000
3. Respon Rangkaian CR Terhadap Square Wave
Suatu rangkaian resistansi kapasitif dengan input gelombang square dari Gambar
2.5(a). Tegangan pada kapasitor pertama akan naik dari nol ke suatu level e1
pada waktu t1 lihat gambar 2-5 (b) Antara t1 dan t2 tegangan yang diberikan
adalah nol sehingga capacitor discaharge ke e2 volt. Kemudian kapasitor mengisi
ke suatu level yang baru e3 pada waktu t3. Untuk menentukan level dari ec
setiapwaktu yang lebih besar dari t2 kebutuhan pertama untuk menghitung e1
pada t1 kemudian e2 dihitung menggunakan e1 sebagai tegangan inisial pada
kapasitor dan tidak ada tegangan input adalah nol dari t1 ke t2. Antara t2 dan t3
tegangan inisial adalah e2 volt dan tegangan input
lebih besar dari nol lagi.
Pada t=4 ms
ec  20V  (20V  0)e 4ms/1uFx3.3KΩ
= 14.05 V [ e1 pada gambar 2-5 (b) ]
dari t=4 ms sampai t=8 ms, E=0 V dan Eo =14.05V
ec  0V  (0  14.05)e 4ms/1uFx3.3KΩ
= 4.18 V [e2 pada gambar 2-5(b)]
Dari t=8 ms ke t=12 ms, E=20V dan Eo = 4.18 V
Pada t=12 ms,
ec  20V  (20V  4.18)e 4ms/1uFx3.3KΩ
= 15.29 V [e3 pada gambar 2-5(b)]
Dari t=12 ms ke t=16 ms E=0 dan E0=15.29 V
Pada t=14 ms
ec  0V  (0V  15.29V)e 4ms/1uFx3.3KΩ
setelah beberapa interval-interval pengisian, pengisian sebagian, pengisian ulang
tegangan kapasitor pada akhir nya akan mencapai kondisi yang tetap (settled).
Ketika kondisi ini terjadi , kapasitor selalu diisi ke level tegangan maksimum,
Emax dan pembuangan ke level yang minimum ,Emin seperti pada gambar 2-5 c.
Level akhir tersebut terjadi ketika tegangan pengisian dan pengosongan adalah
sama. Pada gambar 2-5 (c) E1=E2 juga Emax=E1 dan Emin=(E-Emax)
perhittungan E min dimulai dari E0=Emax dan E=0V,
Emin  ec  0V  (0V  Emax)e  t/CR
= Emax e
 t/CR
Dan sejak
E min =(E-Emax)
E - Emax  Emax e  t/CR
E  Emax e  t/CR  Emax
= Emax
Emax 
(e  t/CR  1) dan
E
1  e  t/CR
2-14
Arus pengisian untuk rangkaian dari gambar 2-5(a) dapat dengan mudah dihitung
dengan menggunakan rumus:
ic 
E  ec
R
Untuk rangkaian pada gambar 2-5(a) tentukan level maksimun dan minimum
pada saat tegangan kapasitor akan stabil.
Pemecahan:
Berdasarkan pada persamaan (2-14):
Emax 
Emax 
E
1  e  t/CR
20 V
1 e
 4 ms/(1uFx3.3K )
Emax = 15.41V
Emin = E-Emax
= 20V-15.41V = 4.59V
4. Rangkaian Integrating
Gambar 2-6 menunjukkan suatu rangkaian RC dengan input gelombang kotak
dan tegangan output pada kapasitor. Bentuk dari gelombang output tergantung
dari hubungan antara waktu constant (CR) dan lebar pulsa (PW).
Mempertimbangkan
dari kasus CR lebih kecil dari PW [gelombang (a) pada
gambar 2-6]. Didalam bagian 2-1, telah di demonstrasikan bahwa kapasitor diisi
ke 99.3% dari tegangan input setelah t=5 CR;
Misal kan
CR 
1
PW
10
Kemudian :
1
PW)
10
ec =99.3% dari E pada t  5(
Sehingga :
ec  E pada t 
1
PW
2
dalam kasus ini output secara kasar mendekati input gelombang kotak. Jika CR
dibuat lebih kecil dibanding dengan
1
PW, kemudian output lebih mendekati
10
menyerupai input gelombang kotak.
Untuk gelombang (b) didalam gamabar 2-6 , CR adalah sama dengan lebar pulsa.
Dalam bagian 2-1 telah capasitor mengalami pembuangan ke 63.2% dari
tegangan input setelah t=CR. Gelombang yang tetap adalah ampiltudo yang lebih
kecil dari 63.2% dari E. Dibawah kondisi dari gelombang dari kapasitor mulai
untuk mendekati bentuk segitiga.
Ketika CR dibuat sama ke 10 kali dari lebar pulsa , hasilnya bentuk gelombang
gambar 2.6 (c). Dalam kasus ini rangkaian CR, dinamakan rangkaian integrator.
Untuk
mengerti
bagaimana
cara
rangkaian
ini
bekerja
penting
dalam
perhitungan level tegangan output didalam hubungan nya dengan waktu. Pada
CR=10xPW, gunakan persamaan 2-2 diperoleh:
ec2  E  (E  Eo)e  PW/10PW
 E  Ee 1 / 10 untuk Eo=0
Untuk menghitung ec1 pada
1
PW :
2
ec1  E  Ee 1/2PW/10PW
= E  Ee
1/20
= E(1-0.95)
= 0.05 E
Hasil ini menunjukkan setelah t1, ec1 =0.05 E dan setelah t2=2t1, ec2+0.1E.
sehingga ec1  2ec1 ketika t2=2t1.
5. Rangkaian Differentiating
6. Efek Pembebanan pada Rangkaian Differensial dan Integral