1. Lapisan Rangkap Listrik

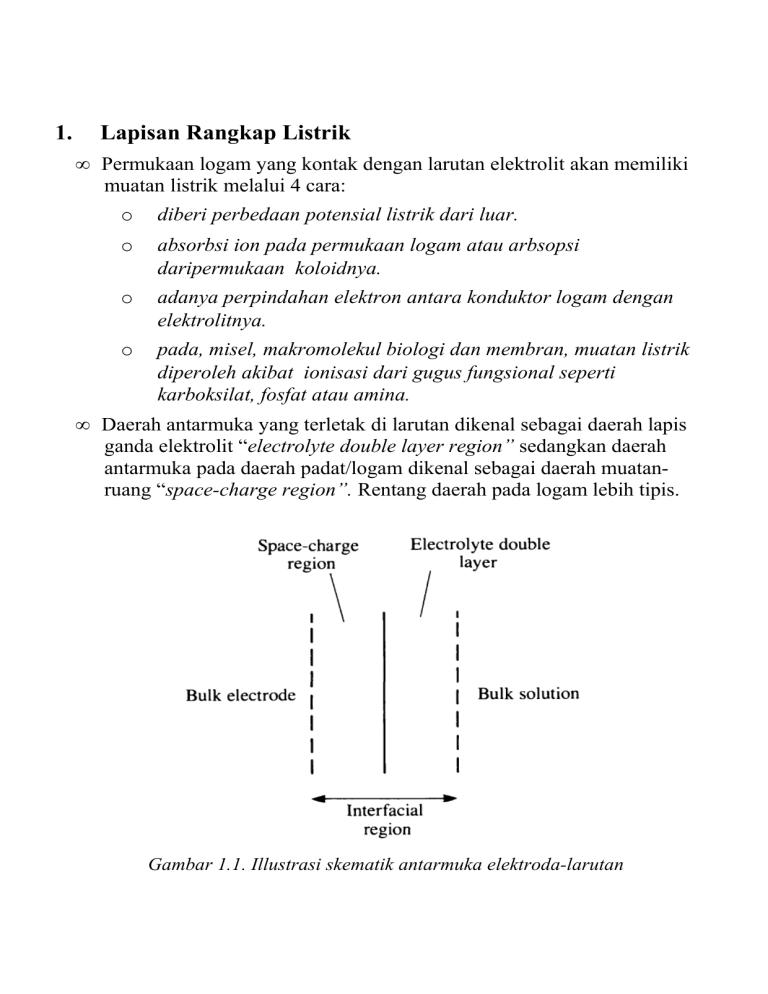
1.
Lapisan Rangkap Listrik
• Permukaan logam yang kontak dengan larutan elektrolit akan memiliki
muatan listrik melalui 4 cara:
o
diberi perbedaan potensial listrik dari luar.
o
absorbsi ion pada permukaan logam atau arbsopsi
daripermukaan koloidnya.
o
adanya perpindahan elektron antara konduktor logam dengan
elektrolitnya.
o
pada, misel, makromolekul biologi dan membran, muatan listrik
diperoleh akibat ionisasi dari gugus fungsional seperti
karboksilat, fosfat atau amina.
• Daerah antarmuka yang terletak di larutan dikenal sebagai daerah lapis
ganda elektrolit “electrolyte double layer region” sedangkan daerah
antarmuka pada daerah padat/logam dikenal sebagai daerah muatanruang “space-charge region”. Rentang daerah pada logam lebih tipis.
Gambar 1.1. Illustrasi skematik antarmuka elektroda-larutan
2
3.1 Lapisan Ganda Rangkap Listrik.
• Bila permukaan logam yang bermuatan listrik kontak dengan larutan
elektrolit, permukaan tersebut akan menarik muatan yang berlawanan
dan menolak muatan yang sejenis.
• Akan terbentuk lapisan ganda muatan listrik, yaitu lapisan pada
‘permukaan logam’ dan lapisan pada ‘permukaan dekat logam’ yang
memiliki muatan yang berbeda.
• Beberapa model Lapisan-ganda Rangkap Listrik dikemukakan oleh
Helmhotz, Gouy-Chapman, dan Stern.
Model Helmhozt, beda potensial antara titik tertentu di LRL dgn fasa
ruah adalah linear, semakin jauh dari elektroda semakin kecil hingga
mencapai nol.
Gouy Chapman, memperhitungkan adanya gerakan termal dari ion-ion.
Stren, gabungan dari Helmholzt dan Guy-Chapman;
Gambar 1.2. Beberapa model lapis rangkap listrik.
3
Gambar 1.3.
Generall representation of the double layer
formed at the metal-electrolyte interface.
(http://www.springer.com/cda/content/document/cda_downloaddocument/9783540422297c1.pd
f?SGWID=0-0-45-93943-p1396491)
3.2 Lapis ganda listrik : Tegangan permukaan, kerapatan muatan
dan kapasitas
• Daerah antarmuka pada suatu larutan adalah daerah yang memiliki harga
potensial listrik,  , yang berbeda dibandingkan dengan fasa ruahnya.
• Terdapat penataan muatan positif dan negatif dimulai dari permukaan
elektroda hingga ke fasa ruah.
• Kapasitas lapis ganda adalah kontanta perbandingan antara potensial
yang diberikan dengan muatan terhadap spesi dalam daerah antarmuka.
Besarnya kapasitas lapis ganda pada berbagai potensial dapat dilakukan
dengan teknik impendasi atau pengukuran elektrokapilaritas. Metoda ini
diperkenalkan oleh Lippmann.
4
Gambar 1.4. Skematis alat pengukuran tegangan permukaan air
raksa dengan metoda Lippmann.
Gambar 1.5. Example of the influence of an electric field on a
liquid structure. The water flowing from the tap in
a bathroom is deviated by the electric field
produced by a plastic hair-brush electrostatically
5
charged by friction on a sweater.(http://www.isisulp.org/lbc/Group/www/JC/thesis/node3.html)
Gambar 1.6. The electrowetting effect. The contact angle of a
conducting drop on an insulated conducting
substrate is modulated by an applied voltage.
(http://www.isis-ulp.org/lbc/Group/www/JC/thesis/node3.html)
• Prinsip utama dalam pengukuran ini adalah kolom kapiler yang diisi
dengan air raksa hingga tinggi h di beri beda potensial akan berada pada
ketinggian yang sama. Pada kondisi ini tegangan permukaan akan
diimbangi dengan gaya gravitasi, sehingga:
2
2  r c  cos  =  r c  Hg h g
(1.1)
dengan r c = jari-jari kapiler;  = sudut kontak;  = tegangan
permukaan;  Hg = rapat massa air raksa.
• Aluran  terhadap E dikenal sebagai kurva elektrokapiler. (Lihat
Gambar 1.7.a).
• Fluks massa untuk percobaan ini adalah
2
 r c  Hg h
m1 =

dengan  adalah waktu hidup tetes (drop lifetime).
(1.2)
• Substitusi persamaan 1.2 ke dalam persamaan 1.1 akan memberikan
2  r c  = m1 g t
(1.3)
• Aluran  terhadap E akan memberikan Gambar 1.7.a. Sedangkan
konversi  menjadi kapasitas diperoleh dengan penurunan ganda
terhadap perbedaan potensial,  , antara logam/elektroda,  M dengan
larutan,  S . Turunan pertama akan memberikan muatan pada permukaan
yang dikenal sebagai persamaan Lippmann
∂
(1.4)
=− M = S
∂ 
6
dengan  M = muatan pada logam (charge on metal) dan  S = muatan
pada larutan. Dan  M  S =0 .
Gambar 1.7. Aluran skematik pada daerah rangkap. (a) tegangan
permukaan vs potensial) (b) kerapatan muatan
elektroda vs potensial (c ) kapasitas diferensial
terhadap potensial.
• Bila diambil potensial pembanding sembarang dan potensial yang
berhubungan dengan potensial pembanding tersebut adalah E  maka
∂  ~ ∂ E   dan
∂
=− M
∂ E
(1.5)
• Persamaan Lippmann merupakan persamaan differensial dari
elektrokapilaritas menunjukkan bahma muatan  M bernilai nol saat
7
kemiringan kurva elektrokapilaritas adalah nol. Potensial dititik ini
disebut sebagai titik muatan nol, E Z .
• Turunan kedua dari kurva elektrokapilaritas akan memberikan nilai
kapasitas diferensial, yaitu kapasitas diferensial , C d , dan kapasitas
integral C i :
Cd =
∂M
(1.6)
∂ E
• Kapasitas integral diperoleh dari
∂ M
Ci =
E−E z
(1.7)
E
∫E C d dE
= E
∫E dE
z
(1.8)
z
3.3 Medan Listrik dan Kapasitas listrik (Electric fields and
capacitance)
• Bila pada dua buah konduktor yang dipisahkan satu sama lain diberikan
potensial listrik, maka akan terbentuk suatu medan listrik pada daerah
yang memisahkan kedua konduktor tersebut.
• Walau “medan listrik” ini sulit untuk dibayangkan adanya. Medan ini
sama dengan medan magnet yang sifatnya tidak terlihat namun
pengaruhnya dapat dirasakan.
• Pada medan listrik terdapat 2 hal yang penting yaitu : Kekuatan medan
(field force) dan fluks medan (field flux).
• Field Force = kekuatan dari medan pada jarak tertentu. (the amount of
“push” that a field exerts over a certain distance)
• Field Flux = jumlah total atau pengaruh medan dalam ruang (the total
quantity, or effect, of the field through space).
• Analogi dengan gaya listrik VOLTAGE (push) dan CURRENT (flow)
8
Gambar 1.8. Medan listrik yang muncul saat 2 buah konduktor
diberi suatu potensial.
• Secara matematika, akan berlaku hubungan Hukum Ohm untuk kapasitor:
dv
i=C
dt
dengan i besarnya arus yang melalui suatu kapasitor; C adalah
dv
capasitansi dalam Farad;
adalah perubahan potensial persatuan
dt
waktu.
• Faktor yang mempengaruhi kapasitansi:
Luas
Jarak
Jenis Material dielektrik
9
• Besarnya kapasitas untuks suatu konduktor mengikuti rumus
A
C=
d
dengan C adalah kapasitansi dalam Farad;  permisivitas (absolut); A
luas permukaan plat dalam m2; d jarak antara plat dalam m.
Material
Relative permittivity (dielectric constant)
============================================================
Vacuum ------------------------- 1.0000
Air ---------------------------- 1.0006
PTFE, FEP ("Teflon") ----------- 2.0
Polypropylene ------------------ 2.20 to 2.28
ABS resin ---------------------- 2.4 to 3.2
Polystyrene -------------------- 2.45 to 4.0
Waxed paper -------------------- 2.5
Transformer oil ---------------- 2.5 to 4
Hard Rubber -------------------- 2.5 to 4.80
Wood (Oak) --------------------- 3.3
Silicones ---------------------- 3.4 to 4.3
Bakelite ----------------------- 3.5 to 6.0
Quartz, fused ------------------ 3.8
Wood (Maple) ------------------- 4.4
Glass -------------------------- 4.9 to 7.5
Castor oil --------------------- 5.0
Wood (Birch) ------------------- 5.2
Mica, muscovite ---------------- 5.0 to 8.7
Glass-bonded mica -------------- 6.3 to 9.3
Porcelain, Steatite ------------ 6.5
Alumina ------------------------ 8.0 to 10.0
Distilled water ---------------- 80.0
Barium-strontium-titanite ------ 7500
• Kapasitor serial dan parallel
10
Kapasitor dalam disusun secara seri
C total =
1
1 1 1
  ....
c1 c2 c3
Kapasitor disusun secara paralel c total =c 1c 2 c 3...
3.4 Model Helmholtz (1879)
• Model ini memodelkan ada keteraturan dalam penataan muatan positif
dan negatif pada kedua sisi dari antarmuka elektroda.
• Model ini mirip dengan menggambarkan keadaan suatu kapasitor plat
paralel dengan permukaan elektroda sebagai salah satu plat dan sisi plat
lain terbentuk dari ion-ion yang menempel pada permukaan elektroda.
11
Gambar 1.9. Lapis rangkap listrik yang mirip dengan kapasitor
elektrik yang terbentuk dari 2 plat yang berbeda
muatan yang dipisahkan dengan jarak tertentu.
Model ini mirip dengan model LRL Helmholzt.
Gambar 1.10. Model Helmholtz untuk lapis rangkap listrik. (a) penataan
ion secara kaku. (b) Variasi potensial elektrostatik sebagai fungsi dari
jarak (c) variasi Cd terhadap potensial yang di berikan.
• Besarnya harga kapasitas (capacity) adalah

C d , H = r 0 (1.9)
xH
dengan x H merupakan jarak antara titik terdekat dari muatan, dan r
adalah permisivitas relatif (relative permittivity) dan 0 = permisivitas
vakum (permittivity of vacuum).
-2
• Nilai r biasanya adalah 6-7, sehingga C d , H =10  F cm .
• Turunnya potensial dari  M ke  S bersifat linier, dan C d , H bukan
merupakan fungsi potensial yang diterapkan pada elektroda
12
• Kekurangan dari model Helmholtz adalah.pada model ini interaksi ionion yang terletak lebih jauh tidak diperhitungkan dan faktor konsentrasi
tidak ikut diperhitungkan juga.
3.5 Model Gouy-Chapman (1910-1913).
• Model ini dikembangkan secara terpisah oleh Gouy dan Chapman dengan
memperhatikan besarnya potensial yang diberikan pada elektroda dan
konsentrasi dari larutan.
• Pada model ini lapisan rangkap listrik tidak akan kompak/padat seperti
pada LRL Helmholtz, tetapi ion bebas bergerak, lapisan ini dikenal
sebagai lapis rangkap baur (diffuse double layer). Tebal lapis rangkap
ini juga tidak kompak namun mempunyai ketebalan yang bervariasi.
Lihat Gambar 1.11.a
Gambar 1.11. Lapis rangkap listrik model Gouy-Chapman. (a)
Penataan ion pada permukaan berlangsung
dengan model difusi. (b) Variasi potensial
elektrostatik terhadap jarak.(c) Variasi C d
terhadap jarak,
13
• Pada model ini distribusi dari spesi ion terhadap jarak dari permukaan
elektroda akan mengikuti hukum distribusi Boltzmann
n i=n0i exp
[
−z i e 
kBT
]
(1.10)
0
dengan =− S dan n i merupakan konsentrasi numerik dari ion i
dalam fasa ruah.
Dengan membagi larutan menjadi ketebalan dx maka pada jarak x dari
permukaan elektroda kerapatan muatan (charge density) untuk semua
ion i adalah :
 x=∑ ni z i e
(1.11)
i
=∑ n0i z i e exp
i
[
−z i e 
kBT
]
(1.12)
• Persamaan Poisson yang menghubungkan antara potensial dengan
distribusi muatan adalah
2
∂   x 
 x
=−
(1.13)
2


∂x
r 0
Dengan menggabungkan 1.12 dengan 1.13 maka akan diperoleh
persamaan Poisson-Boltzmann

2
−zi e 
∂   x 
e
0
=−
n
z
exp
∑
2
r 0 i i i
kBT
∂x

(1.14)
• Persamaan ini sama dengan perlakuan interaksi ion pada larutan elektrolit
encer yang diberikan oleh Debye-Huckel, dengan x sebagai ion pusat .
Pada kasus Debye-Huckel, ion pusat adalah kecil dan  bernilai kecil
2
maka akan dapat dibuat pendekatan  e  /k B T  ≪1, dan dengan
menggunakan suku pertama dari ekspansi ekponensial.
• Untuk suatu elektroda yang memiliki dimensi yang jauh lebih besar
dibandingkan ion, pendekatan linear tidak bisa diterapkan.
• Untuk menyelesaikan 1.14 maka digunakan sifat dari turunan,
14
2
2
 
∂   x 
1 ∂ ∂ 
=
2
2 ∂  ∂ x
∂x
(1.15)
• Dengan cara ini maka persamaan Poisson-Boltzmann dapat disusun ulang
menjadi
2
 
∂ 
∂x
=−


−z i c 
2e
n0i zi exp
d
∑
r 0 i
k BT
(1.16)
Integrasi dilakukan dengan menggunakan kondisi batas berikut:
x=0
 =   ,0
(1.17)
x ∞
 0
∂  /∂ x=0
akan diperoleh,
2
 
∂ 
∂x
=
2k B T
 r 0
[ 
∑ n 0i exp
i
 ]
−zi e  
−1
kBT
(1.18)
Untuk elektrolit z:z
∂ 
=
∂x

0 1/ 2
8 k T ni
r  0
  
sinh
z e 
2 kT
(1.19)
Persamaan 1.19 dapat diintegrasi jika ditulis dalam bentuk

∫
,0
[
0 1/ 2

 ]
d 
z e 
sinh
2 kBT
8 k B T ni
=−
 r 0

x
∫0 dx
(1.20)
¿
Hasil integrasinya adalah
] 
[
0 1/ 2
2kbT
tanh  z e  /4 k B T 
8 k B T ni
ln
=−
ze
tanh  z e   ,0 / 4 k B T 
r  0

x
(1.21)
Yang dapat disusun ulang menjadi
[
]
tanh  z e  / 4 k B T 
=exp [−x / x DL ]
tanh  z e  , 0 / 4 k B T 
dengan x DL adalah jarak karakteristik dari tebal lapis difusi
(1.22)
15

x DL=
r 0 k B T
0
2
2 ni z e
2
1/ 2

(1.23)
-8 -1 -1/2
Untuk air  r =78 pada 298 K, x DL=3.04×10 z c cm
Besarnya nilai C d diperoleh dari 1.19. Kerapatan muatan (charge
density) dari lapisan baur adalah
 M = r 0
 
∂ 
∂x
x=0
=8 k T r 0 n0i 1/ 2 sinh

z e  , 0
2 kBT

setelah dilakukan dideferensiasi
∂ M
C d , GC =
∂  ,0
=

2
2
0 1/2
2 z e r 0 n i
kBT

cosh

z e  , 0
2 kBT

• Nilai cosh memberikan kenaikkan pada variasi dalam kapasitas dengan
bentuk potensial yang terlihat pada Gambar 1.11. Puncak minimum dari
kurva di indentifikasi sebagai titik muatan nol, E z dan bentuk kurva akan
simetri sekitar E z
• Untuk larutan encer pada suhu 2980 K
1 /2
−2
C d , GC = 228 z c∞ cosh 19.5 z   ,0  F cm
• Model ini lebih baik dibandingkan dengan model kapasitor plat paralel,
namun model ini hanya berlaku untuk harga E yang dekat ke E z . Harus
diingat bahwa pada permukaan konsentrasi adalah tinggi.
16
3.6 Kelemahan teori Gouy-Chapman.
•
Ci
=exp
0
Ci
•

−z i F 
RT

ni


−z i e 
,
kT
ni
Bila dikonversi ke satuan molar dan e /k =F / R maka persamaan
Boltmann ini menjadi
Dari Persamaan 1.11 dapat disusun ulang menjadi
0 =exp
(1.12)
Pada kasus larutan NaCl 1 M yang mengalami kontak dengan
permukaan yang memiliki potensial  a=0.1V . Maka berdasarkan
persamaan 1.11, konsenstrasi ion klorida pada permukaan (di luar
lapisan Helmholtz) akan sebesar 49M !! Kira-kira 30 ion klorida per
nanometer kubik.
Tolakkan antar ion pada struktur seperti diatas akan jauh lebih besar
dari gaya tarik elektrostatik yang ada. Sehingga pada kasus ini
pendekatan yang dilakukan tidak tepat, karena saat kita melakukan
pendekatan interaksi elektrostatik antar ‘ion di larutan’ – ‘permukaan’
di perhitungkan tetapi interaksi antar ion di larutan di lupakan.
Pendekatan yang dilakukan akurat untuk larutan encer namun tidak
untuk larutan yang pekat.
•
Asumsi bahwa kerapatan muatan  bersifat fungsi yang kontinu dari
jarak ke permukaan adalah tidak 100% pada tingkar makroskopik. Tapi
pendekatan ini dibenarkan jika fungsi waktu juga ikut diperhitungkan,
yaitu karena adanya gerakkan termal dari ion.
•
Penggunaan konstanta dielektrik larutan untuk gaya-gaya elektrostatik
jarak pendek tidak pas, karena pada jarak pendek momen dipol air
terorientasi di sekitar ion atau pada permukaan bermuatan, sehingga
sifat-sifat dielektrik di dekat permukaan tentunya berbeda dengan yang
di dalam larutan dalam/ruah (bulk).
• Pendekatan Gouy-Chapman ini sebaiknya di gunakan untuk mengamati
sifat kualitatif atau semi kuantitatif dari sistem lapisan listrik ganda
bukan aspek kuantitatifnya. Karena pendekatan kualitatifnya adalah
akurat.
17
3.7 Model Stern (1924)
• Model Stern menggabungkan model Helmholtz untuk potensial yang
memiliki besar yang jauh dari E z dan model Gouy-Chapman untuk nilai
potensial yang dekat dengan E z .
• Lapis rangkap listrik yang kompak/padat terbentuk oleh lapisan ion pada
lapis pertama yang dekat dengan elektroda dan kemudian diikuti dengan
lapisan yang baur hingga fasa ruah dari larutan.
Gambar 1.13. Model lapis rangkap lisrik menurut Stern. (a)
Pengaturan ion yang kompak dan diikuti dengan
lapis yang baur. (b) Variasi potensial elektrostatik
terhadap jarak dari elektroda. (c ) Variasi C d
dengan potensial.
• Secara fisik pada potensial yang jauh dari E z elektroda menarik ion-ion
dengan kuat sehingga ion tersebut terikat secara kuat, sedangkan pada
potensial yang dekat dengan E z ion tersusun secara baur.
• Dalam bentuk matematika model ini mirip dengan dua buah kapasitor
yang disusun secara seri, sehingga.
18
1
1
1
=

Cd
c H C GC
=
xH
1

r 0  2   z 2 e 2 n0 / k T 1/ 2 cosh z e  /2 k

r 0
i
B
 ,0
bT 
(1.24)
(1.14)
• Bidang yang memisahkan antara kedua zone (Helmholtz vs GouyChapman) disebut sebagai Outer Helmholzt Plane (OHP).
3.8 Model Grahame (1947)
• Pada model ini ditambahkan faktor adsorpsi spesifik. Gambar 1.15
Gambar 1.15. Model Grahame untuk lapis rangkap listrik (untuk
elektroda merkuri).
• Adsorpsi spesifik : ion adsorpsi spesifik yang kehilangan solvasinya yang
mendekati permukaan elektroda. Ion ini dapat memiliki muatan yang
sama maupun berlawanan dari elektroda.
19
3.9 Model Bockris, Devanathan dan Muller (1963)
• Pada model ini faktor pelarut yang bersifat polar (dipolar), misal seperti
air. Pada pelarut yang bersifat polar ini interaksi antara elektroda dengan
dipolnya harus juga ikut diperhitungkan.
• Hal ini sangat penting, meningat bahwa konsentrasi pelarut adalah jauh
lebih besar dari konsentrasi zat terlarut. Sebagai contoh air murni
memiliki konsentrasi 55.5 mol dm-3.
Gambar 1.16. Model Lapis Rangkap Listrik Bockris dkk.
>>>>>>>>>>>>>>>>>>>>>>>> ***********************
3.10 Adsorpsi Spesifik
• Berdasarkan model lapis rangkap listrik Grahame adsorpsi spesifik
adalah adsorpsi ion pada permukaan elektroda setelah ion tersebut
kehilangan sebagian atau seluruh proses solvasinya. Muatan ion yang
teradsorpi dapat sama dengan muatan elektroda namun bisa juga berbeda.
• Menurut IUPAC, Solvasi adalah interaksi antara zat terlarut dengan
pelarut yang akan meningkatkan kestabilan zat terlarut dalam larutannya.
20
Gambar 1.17. Gambar solvasi ion natrium dalam air.
• Adanya adsorpsi spesifik diperlihatkan oleh karakteristik kurva
elektrokapilaritas untuk elektroda merkuri dapat berbeda bila elektrolit
yang di gunakan berbeda pada konsentrasi yang sama.
Gambar 1.18. Kurva elektrokapilaritas untuk merkuri yang kontak
dengan berbagai jenis elektrolit.
21
• Dari kurva pada Gambar 1.18 terlihat bahwa untuk Na-Halida dan Khalida perbedaan mulai muncul pada nilai potensial positif untuk E Z ,
dan ini diduga karena interaksi yang terjadi adalah dengan anionnya.
Pengaruhnya bertambah besar bila jari-jari anion bertambah kecil.
• Besarnya adsorpsi spesifik juga berkorelasi dengan konsentrasi elektrolit,
seperti halnya akan terjadi perubahan pada titik nol muatan yang
dikarenakan oleh spesisfik adsorpsi dari muatan. Hal ini dikenal sebagai
efek Esin-Markov, yang besarnya adalah;
=

1 ∂ E Z 
RT ∂ ln a
 
=
M
∂ E Z 
∂

(1.25)
M
• Turunan ini bernilai nol bila adsorpsi spesifik tidak ada. Untuk adsorpsi
anion, dengan rapat muatan yang konstan, titik muatan nol bergeser ke
arah negatif sehingga terjadi kesetimbangan kembali akibat adanya
adsorpsi. Untuk kation, E Z bergerak ke arah yang positif. Dalam larutan
yang encer, adsorsi spesifik hanya terjadi untuk daerah yang dekat pada
EZ.
•
Percobaan menunjukkan bahwa adsorpsi spesifik lebih sering terjadi
pada anion dibandingkan pada kation. Hal ini dapat difahami melalui
model antarmuka permukaan. Karena kisi logam merupakan kisi kation
dalam lautan elektron yang bergerak dengan bebas, sehingga akan lebih
menarik anion yang berada dalam larutan.
•
Besarnya adsorpsi bergantung pada konsentrasi elektrolit. Besarnya area
penutupan untuk suatu permukaan oleh adsorpsi spesifik dapat
diungkapkan sebagai lapisan monolayer isoterm adsorpsi. Terdapat 3
jenis isoterm adsorpsi yaitu;
Isoterm Langmuir.
•
Dianggap tidak terjadi interaksi antara spesi yang teradsorpsi,
permukaan merupakan permukaan yang licin/halus sehingga dapat
terjadi kejenuhan pada permukaan.
Jika  adalah fraksi yang menutupi permukaan maka,

= a
1− i i ,∞
22
Dengan β i adalah koefisien proporsionalisasi dan ai ,∞ adalah aktifitas
spesi ke-i pada fasa ruah.
Gambar 1.19. Kurva isoterm Langmuir
Isoterm Temkin
Pada isoterm Temkin energi adsorpsi merupakan fungsi dari area
tertutup yang bernilai,
RT
 i=
ln  i a i ,∞ 
2g
Dengan  i adalah spesi i yang berlebih, dan g adalah parameter
interaksi energi antara spesi teradsorpsi yang nilai nya bergantung pada
area yang tertutup.
23
Gambar 1.20. Kurva Isoterm Temkin
Isoterm Frumkin
Interaksi pada isoterm Frumkin mengikuti persamaan;
i
2g  i
i a i ,∞=
exp
 s− i
RT
Atau
 i=

 − i
RT
i a i ,∞ ' ' ln s
i
2g

Dengan  s adalah “maximum surface excess”. g adalah parameter
interaksi, bila bernilai positif maka terjadi gaya atraktif sedangkan
=
negatif adalah gaya tolakkan. Bila g =0 dan Γ i s Γ θ maka
akan
diperoleh isoterm Langmuir. Sedangkan isoterm Temkin dapat
diperoleh bila Γ i s Γ 0.5=
24
Gambar 1.1.
Kurva Isoterm Frumkin.
Adsorpsi dapat dipelajari dengan berbagai macam metoda elektrokimia,
termasuk didalamnya kinetika dari adsorpsinya.
3.11 Elektroda logam padat
• Merkuri tidak bersifat seperti elektroda padat yang umum. Merkuri
bersifat cair sehingga atom merkuri selalu bergerak. Lebih-lebih atom
yang terletak pada permukaan elektroda yang kontak dengan larutan.
• Elektroda logam padat memiliki struktur yang jelas, dapat berupa suatu
polikristalin atau monokristalin. Pada elektroda logam padat proses
konduktansi merupakan proses elektronik yang utama. Konduktansi
terjadi karena terdapat elektron valensi yang dapat bergerak bebas pada
daerah yang dikenal sebagai daerah tingkat Fermi, E F . Dengan adanya
elektron yang bergerak pada tingkat Fermi ini, maka distribusi elektonik
dari atom menjadi meningkat.
• Untuk suatu logam, tingkat kehunian dari tingkat elektronik yang dekat
pada E F diberikan dalam ungkapan
f=
1
 E−E f 
1exp
k BT
(1.26)
25
Dengan f merupakan kebolehjadian tingkat kehunian dari tingkat
energi E dan k B merupakan konstanta Boltzman, f =0.50 saat
E=E F .
• Energi Fermi adalah potensial kimia dari elektron pada elektroda logam.
Jika E=E F k B T maka f =0.27 dan jika E=E F −k B T maka
f =0.73 .
• Gambar 1.21 menggambarkan aluran dari persamaan 1.26; dan pada suhu
nol kerapatan elektron pada daerah Fermi turun dengan tajam, tapi pada
suhu yang lebih tinggi kebolehjadian penempatan ini menjadi lebih
baur/kabur.
Gambar 1.21. Kerapatan elektron yang menempati daerah fermi
pada logam.
• Untuk logam hanya elektron dengan energi k B T dari E F dapat
berpindah tempat.
• Struktur antarmuka dari suatu elektroda logam tergantung pada berbagai
faktor. Jarak antar atom sangat bergantung pada bentuk kristalografi dan
besarnya energi interaksinya.
26
• Antara kristal pada suatu meteri poli-kristalin tredapat 'patahan' dalam
struktur yang memunculkan defek satu dimensi maupun dua dimensi
seperti 'screw dislocation'.
• Variasi elektrostatik sebagai fungsi jarak ditunjukkan pada Gambar 1.22
dan 1.23
Gambar 1.22. Variasi potensial elektrostatik sebagai fungsi
elektroda metalik untuk model klasik.
Gambar 1.23. Variasi potensial elektrostatik sebagai fungsi
elektroda materi untuk model jellium.
27
Gambar 1.24. Variasi potensial terhadap jarak untuk elektroda
logam yang dipisahkan dari larutan elektrolit
tanpa memodifikasi muatan.  Adalah besarnya
potensial saat distribusi muatan relatif terhadap
elektroda dan larutan.
• Model ini berkorelasi dengan model kimia, dan menggambarkan keadaan
bahwa elektron pada elektroda padat akan berpenetasi di daerah yang
sempit pada area larutan. Hal ini terjadi karena adanya sifat gelombang
dari elekron.
• Pada model ini Potensial Galvani atau potensial listrik dalam,  ,
berkaitan dengan E F dan Potensial Volta, potensial listrik luar,  ,
adalah merupakan potensial di luar distribusi elektronik dari elektroda,
kira-kira terletah diluar IHP, 10−5 cm dari permukaan. Selisih antar
kedua potensial ini dikenal sebagai potensial permukaan,  .
3.12 Elektroda semikonduktor.
• Pada elektroda semikonduktor, tingkat elektronik yang dapat di gunakan
lebih terbatas. Pada semikonduktor terdapat pemisahan antara pita
valensi yang terisi dengan pita kondutansi yang kosong. Bila besarnya
28
pemisahan ini lebih dari 3 V. maka benda tersebut dikatakan sebagai
isolator.
• Promosi elektron dari valensi ke kondukansi akan mengakibatkan
timbulnya ‘lubang/hole’ (kekurangan elektron), area yang ini akan
bermuatan positif. Lubang/hole ini dapat yang dapat bergerak melalui
kristal. Akibatnya konduktansi terjadi karena terdapat pergerakkan
elektron pada pita konduktansi dan pergerakkan lubang pada pita valensi.
Gambar 1.25. Model pita untuk suatu semikonduktor. Pada
model ini pita valensi akan terisi secara penuh
oleh elektron dan pita konduktansi akan kosong.
Konduktansi terjadi karena adanya elektron yang
dipromosikan dari Ev ke Ec .
• Promosi elektron pada semikonduktor dari pita valensi ke pita hantaran
dapat terjadi akibat eksitasi secara termal atau foton.
• Letak tingkat energi Fermi adalah ditengah tengah gap-pita. Besarnya
adalah
 E  E c
E
E−F ~ v
=E v  g
2
2
29
• Dengan syarat bahwa besarnya E F diperoleh dari probabilitas
kehuniannya mencapai 0.5.
• Dengan ungkapan dalam energi band gap, E g , dengan mensubsitusi
E=E C , dan E g ≫ kT banyaknya elektronyang dapat tereksitasi adalah.
n ∝exp
Tabel 1.1
 
−E g
2k b T
Bandgap energy, E g , dan panjang gelombang  g
dari beberapa semikonduktor .
• Keadaan elektronik lain yang akan ada pada sebuah permukaan
semikonduktor adalah karena teradsorpsinya suatu spesi atau terjadi
reorganisasi permukaan. Keadaan ini juga dapat membuat terjadi transfer
elektron antara elektroda dengan larutan.
• Bila semikonduktor merupakan padatan ionik. Maka konduktansi dapat
merupakan konduktansi elektronik atau ionik. Konduktansi ionik
terbentuk karena adanya defek pada kristal yang dapat mengalami
pergerakkan. Jenis defek yang bersifat sepertin ini adalah Defek Frenkel
dan Defek Schotty.
30
• Untuk memudahkan dalam pengamatan, dan karena mayoritas
semikonduktor bersifat tidak ionik maka yang diperhatikan adalah faktor
konduktor elektronik.
• Karena elektron sulit bergerak pada semikonduktor, saat keadaan steady
state tercapai, akan tercipta daerah variasi potensial yang terletak pada
space charge region. Pada suatu semikonduktor intrinsik (kristal yang
murni), hal ini tidak banyak bermanfaat.
Gambar 1.26 Daerah space-change region pada suatu
semikonduktor.
• Lebih umum dipakai semikonduktor yang di kotori (doped), proses
doping ini dilakukan secara eksternal.
• Pada semikonduktor tipe-n, doping ini dilakukan dengan cara
memasukkan atom yang ukurannya sama dengan atom dalam kisinya
namun memiliki elektron yang lebih banyak. Misalnya silikon di doping
dengan menggunakan fosfor atau arsenik
• Dengan cara ini maka atom akan menempati posisi kristal dan akan
mensupply elektron yang dapat bergerak melalui kisi kristal. Energi dari
31
elektron ini lebih kecil sedikit dari E c . Konduktansi elektronik dapat
dilakukan dengan cara eksitasi termal dari pita yang tidak murni ke pita
konduktansi.
• Pada semikonduktor tipe-p, maka proses doping dilakukan dengan
memasukkan atom yang memiliki defisiensi elektron dibandingkan
dengan atom semikonduktornya. Energi atom ini lebih tinggi sedikit dari
E v , lubang konduktansi pada pita valensi terjadi akibat promosi elektron
dari E v ke pita yg kosong.
• Dengan cara doping, sangat mungkin untuk merubah suatu senyawa
padat yang bersifat insulator (karena bandgap lebar), menjadi suatu
konduktor. Dalam elektrokimia proses doping ini dilakukan dengan cara
membuat E F dekat ke E c (tipe-n), atau dekat ke E v (tipe-p)
Gambar 1.27. Semikonduktor: (a) tipe-n; (b) tipe-p. Modus
konduktansi elektron ditunjukkan oleh arah anak
panah.
32
Grafik 1.28
Jenis daerah -space charge region pada
semikonduktor tipe-n, tergantung pada potensial
yang di kenakan pada potensial pita U fb , U
adalah potensial (V) dan E c adalah potensial
yang berhubungan E c dekat ke permukaan.
sur
33
Gambar 1.29.
• Karena daerah space-charge region, hampir semua drop potensial dapat
terjadi. Sehingga kapasitasnya dapat dicari, C sc , dan darinya dapat
dihitung E fb dengan menggunakan persamaan Mott-Schotty.
[
]
k T
2
U −U fb − B

e r 0 N D
e
dengan N D adalah kerapatan dari atom donor.
−2
C sc =
• Setelah E fb diketahui, dapat dihitung E v dan E c dari persamaan
N
E v =−E fbk B T ln D semikonduktor tipe p
Nv
E c =E fbk B T ln
ND
semikonduktor tipe n
Nc