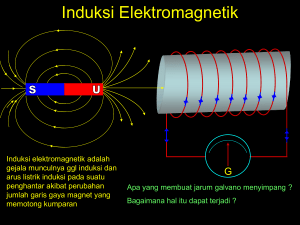
165 BAB 7 RANGKAIAN GANDENG MAGNETIK 7.1

BAB 7
RANGKAIAN GANDENG MAGNETIK
7.1 Pendahuluan
Bilamana dua buah rangkaian atau lebih yang terhubung secara langsung atau
tidak satu sama lainnya, akan tetapi mempunyai pangaruh antara satu sama lainnya
secara magnetik, diakibatkan adanya medan magnet disalah satu rangkaian tersebut,
maka rangkaian tersebut dikatakan rangkaian gandeng magnetik ( magnetically couple).
Pada beberapa peralatan listrik yang dibuat berdasarkan prinsip di atas, misalnya
seperti transformator yang dipergunakan pada sistem tenaga listrik yang fungsinya untuk
mentransfer energi listrik dari suatu loop ke loop yang lainnya pada frekuensi tetap.
Transformator ini ada yang disebut sebagai transformator penaik tegangan (step up) atau
sebagai penurun tegangan (step down), dan selain itu transformator juga pada peralatan
elektronika.
7.2 Induktansi Timbal Balik (Mutual Indutance)
Apabila dua buah induktor / kumparan / koil (N1 dan N2) yang berdekatan satu
sama lainnya, dan bilamana salah satu kumparan dialiri oleh arus (misalnya N1) tersebut
akan timbul fluksi magnetik, dimana fluksi ini ada yang merambat ke kumparan N2, yang
mana fluksi yang merambat ke kumparan N2 akan menimbulkan tegangan pada
kumparan N2 (sering disebut sebagai tegangan induksi), maka fenomena di atas dikenal
dengan induksi timbal balik (mutual indutance). Sebagai ilustrasi perhatikan gambar
rangkaian di bawah ini :
Gambar 7.1 Fluksi magnetik yang dibangkitkan pada kumparan dengan N belitan.
165
Gambar di atas memperlihatkan sebuah kumparan dengan banyak belitan N.
Bilamana arus i mengalir melalui kumparan tersebut, maka disekeliling kumparan akan
timbul fluksi magnetik φ, dan berdasarkan hukum Faraday, pada kumparan akan terjadi
tegangan induksi sebesar v yang sebanding dengan perkalian jumlah belitan N dengan
perubahan fluksi φ perwaktu, atau dapat dinyatakan dengan :
vN
d
dt
(7.1)
akan tetapi karena fluksi φ yang dihasilkan oleh arus I, maka dapat dikatakan perubahan
fluksi φ juga diakibatkan oleh perubahan arus, atau dituliskan dengan :
vN
d di
.
di dt
(7.2)
Sebagaimana diketahui bilamana sebuah induktor dialiri arus, maka akan terjadi
tegangan pada induktor tersebut sebesar :
vL  L
di
dt
(7.3)
karena v = vL, maka dari persamaan (7.2) dan (7.3) diperoleh :
LN
d
dt
(7.4)
dimana L adalah persamaan (7.4) dikenal dengan induktansi diri (self-indutance).
Selanjutnya apabila dua buah kumparan dengan induktansi L1 dan L2 dimana
jumlah belitan masing-masing kumparan adalah N1 dan N2 saling didekatkan satu sama
lainnya yang digambarkan sebagai berikut :
Gambar 7.2 Induktansi timbal balik dari kumparan N2 terhadap kumparan N1
Untuk penyederhanaan, maka diasumsikan kumparan N2 tidak dialiri arus. Oleh
karena kumparan N1 dialiri oleh arus, maka pada kumparan N1 ini timbul fluksi φ1,
166
dimana fluksi ini terbagi menjadi dua bagian yaitu φ11 dan φ12. Fluksi φ11 ini adalah
fluksi yang hanya melingkupi N1, sedangkan fluksi φ12 adalah fluksi yang berasal dari
kumparan N1 yang melingkupi kumparan N2. Sehingga dengan demikian besar fluksi
yang timbul pada kumparan N1 akibat adanya arus yang mengalir pada kumparan ini
dapat dituliskan dengan :
1  11  12
(7.5)
maka walaupun kedua kumparan ini secara fisik terpisah, akan tetapi mereka dikatakan
terhubung secara magnetik.
Karena adanya φ1, maka pada kumparan N1 terjadi tegangan induksi sebesar :
v1 
d1
dt
(7.6)
Selanjutnya karena adanya φ12, maka pada kumparan N2 akan timbul juga tegangan
induksi sebesar :
v2 
d12
dt
(7.7)
Adapun fluksi-fluksi yang ada pada kumparan N1, disebabkan oleh karena adanya
arus i1 yang mengalir pada kumparan N1, yang mana fluksi ini akan menimbulkan
tegangan induksi v1 pada kumparan N1 seperti yang diperlihatkan oleh Persamaan (7.6).
Oleh karena itu Persamaan (7.6) ini dapat dibuat dalam bentuk :
v1  N1
d1 di1
di
.
 L1 . 1
dt dt
dt
(7.8)
d1
dt
(7.9)
dimana :
L1  N1
disebut sebagai induktansi diri (self-indutance) dari kumparan N1.
Demikian pula halnya degan Persamaan (7.7) dapat dubuat dalam bentuk :
v2  N 2
d12 di1
.
di1 dt
(7.10)
bila dimisalkan :
M12  N 2
d12
di1
(7.11)
maka Persamaan (7.10) menjadi :
167
v 2  M12
di1
dt
(7.12)
dimana M21 ini disebut sebgai induktansi timbal balik dari kumparan N2 akibatnya φ12
dari kumparan N1, dimana subskrit 21 mengindikasikan hubungan tegangan induksi pada
kumparan N2 dengan arus pada kumparan N1.
Selanjutnya apabila arus i2 yang mengalir pada kumparan N2, seperti gambar
berikut ini:
Gambar 7.3 Induktansi timbal balik M12 pada kumparan N1 yang diakibatkan kumparan N2
Apabila kumparan N2 dialiri arus i2, maka pada kumparan N2 ini timbul fluksi φ2,
dimana fluksi ini terbagi menjadi dua bagian yaitu φ22 dan φ21. Fluksi φ22 adalah fluksi
yang hanya melingkupi N2 sedangkan fluksi φ21 adalah fluksi yang bersasal dari
kumparan N2 yang melingkupi kumparan N1. Sehingga dengan demikian besar fluksi φ2
yang timbul pada kumparan N2 akibat adanya arus i2 yang mengalir pada kumparan ini
dapat dituliskan dengan :
 2   22   21
(7.13)
Karena adanya 2 , maka pada kumparan N2 terjadi tegangan induksi sebesar :
v2 
d 2
dt
(7.14)
selanjutnya karena adanya  21 pada kumparan N1, maka pada kumparan N1 akan timbul
juga tegangan induksi sebesar :
168
v1  N1
d 21
dt
(7.15)
Adapun fluksi-fluksi yang ada pada kumparan N2, disebabkan oleh karena adanya
arus i2 yang mengalir pada kumparan N2, yang mana fluksi ini akan menimbulkan
tegangan induksi v2 pada kumparan N2 seperti yang diperlihatkan oleh Persamaan (7.14),
oleh karena itu Persamaan (7.14) ini dapat dibuat dalam bentuk :
v2  N2
d 2 di 2
di
.
 L2 2
dt dt
dt
(7.16)
d 2
dt
(7.17)
dimana :
L2  N2
disebut sebagai induktansi diri (self-indutance) dari kumparan N2. Karena pada
kumparan N1, hanya ada  21 , dimana fluksi ini timbul karena adanya arus i2 yang
mengalir pada kumparan N2, oleh sebab itu Persamaan (15) dapat dituliskan :
v1  N1
d 21
d di
di
 N1 21 . 2  M12 2
dt
dt dt
dt
(7.18)
dimana :
M12  N1
d 21
dt
(7.19)
M12 disebut sebagai induktansi timbal balik (mutual-indutance) dari kumparan N1 akibat
adanya fluksi  21 dari kumparan N2.
Dari penganalisaan M21 dan M12, maka dapat disimpulkan bahwa induktansi
timbal balik terjadi karena adanya tegangan induksi pada suatu rangkaian, akibat adanya
perubahan arus perwaktu pada rangkaian lainnya. Hal ini merupakan sifat induktor,
dimana pada suatu induktor akan terjadi tegangan induksi akibat adanya arus yang
merupakan fungsi waktu yang mengalir pada induktor lain yang dekat dengannya,
sehingga dapat dikatakan :
Induktansi timbal balik M yang satuannya dalam henry [H] adalah ukuran
kemampuan suatu induktor untuk menginduksikan tegangan pada induktor lain
yang berdekatan dengannya.
169
Walaupun induktansi timbal balik M selalu merupakan besaran positif, akan
tetapi tegangan timbal balik
M
di
dt bisa berharga positif atau negatif. Adapun salah satu
cara untuk menentukan tanda aljabar dari
M
di
dt , bila arah belitan terlihat dengan jelas
adalah dengan hukum tangan kanan dari Lenz yang mengatakan :
Apabila konduktor diletakkan pada telapak tangan, dan ibu jari-jari tangan
menggenggam kumparan searah dengan arah belitan kumparan maka jari
telunjuk menunjukkan arah arus, sedangkan ibu jari menunjukkan arah fluksi.
(a)
(b)
Gambar 7.4 Aturan tangan kanan (a) untuk tanda M positif (b) untuk tanda M negatif
170
7.3 Aturan Dot
Selain aturan dari tangan kanan Lenz untuk menentukan tanda aljabar dari
M
di
dt ,
masih ada yang disebut aturan Dot (titik), yang mengatakan :
1. Bilamana kedua arus dalam rangkaian gandeng magnetik sama-sama menuju
tanda dot atau sama-sama meninggalkan tanda dot, maka tanda aljabar dari
M
di
dt adalah positif.
(a)
(b)
Gambar 7.5 Aturan dot untuk arus sama-sama menuju atau meninggalkan tanda dot
(a) Sama-sama menuju tanda dot (b) Sama-sama meninggalkan tanda dot
2. Apabila salah satu arus menuju tanda dot, sedangkan yang lain meninggalkan
tanda dot, maka tanda aljabar dari
M
di
dt adalah negatif.
Gambar 7.6 Arus menuju tanda dot dan yang lain meninggalkan tanda dot
Catatan :
171
Adapun yang dimaksud dengan arus menuju tanda dot adalah bilamana tanda
panah arus lebih dahulu mengenai tanda dot baru kemudian tanda kumparan.
Sedangkan yang dimaksud arus meninggalkan tanda dot adalah apabila tanda panah
arus lebih dahulu mengenai tanda kumparan baru kemudian mengenai tanda dot.
Gambar 7.7 Menentukan arus menuju atau meninggalkan tanda dot
7.4 Energi Pada Rangkaian Gandeng Magnetik
Sebagaimana diketahui bahwa energi yang tersimpan pada suatu induktor
adalah :
w
1 2
Li
2
(7.20)
maka untuk menentukan energi yang tersimpan pada suatu rangkaian gandeng magnetik,
perhatikan gambar berikut ini :
Gambar 7.8 Rangkaian untuk memperlihatkan energi yang tersimpan dalam rangkaian gandeng
Adapun pada reangkaian gandeng di atas, diasumsikan bahwa arus-arus i1 dan i2
awalnya adalah nol, sehingga energi yang tersimpan (energy stored) dalam setiap
kumparan adala nol.
172
Kemudian arus i1 dinaikkan/ diperbesar dari nol sampai I1 sedangkan i2 tetap nol,
maka daya pada kumparan L1 adalah :
p1 (t )  v1.i1  i1L1
di1
dt
(7.21)
maka energi yang tersimpan dalam rangkaian adalah :
I1
w1   p1.dt  L1  i1di1 
0
1
L1I12
2
(7.22)
selanjutnya harga i1 = I1 dipertahankan tetap, maka kemudian arus i2 dinaikkan dari nol
sampao I2, maka tegangan induksi timbal balik pada kumparan L1 adalah
M12
di 2
dt ,
sedangkan tegangan induksi bersama pada kumparan L2 adalah nol (karena i1 tidak
berubah dengan perubahan waktu), maka daya pada kumparan L2 ini adalah sebesar :
p 2 ( t )  i1M12
di 2
di
di
 i 2 .v 2  I1M12 2  i 2 .L 2 2
dt
dt
dt
(7.23)
sedangkan energi pada kumparan L2 ini adalah :
I2
I2
w 2   p 2 dt  M12 I1  di 2  L 2  i 2 di 2  M12 I1 I 2 
0
0
1
L2I 22
2
(7.24)
Maka total energi yang tersimpan pada kedua kumparan, bilamana arus i1 dan i2
memiliki harga yang konstan adalah :
w  w1  w 2 
1
1
L1I12  L 2 I 2 2  M 12 I1I 2
2
2
(7.25)
Seandainya peninjauan dibalik, yaitu arus i2 terlebih dahulu dinaikkan dari nol
sampai I2 dan kemudian barulah i1 dinaikkan dari nol sampai I1, maka total energi yang
tersimpan pada kedua kumparan adalah :
w
1
1
L1I12  L 2 I 2 2  M 21I1I 2
2
2
(7.26)
terlihat bahwa energi total yang tersimpan pada kedua kumparan pada Persamaan (7.25)
dan (7.26) adalah sama, dan bilamana kedua persamaan ini disamakan, akan diperoleh :
173
M12  M 21  M
(7.27)
sehingga dapat dituliskan :
w
1
1
L1I12  L 2 I 2 2  M.i1
2
2
(7.28)
Pada Persamaan (7.28) tanda aljabar M diambil positif sesuai dengan Gambar 7.8,
dimana kedua arus i1 dan i2 sama-sama menuju tanda dot, akan tetapi seandainya Gambar
7.8, seperti berikut :
Gambar 7.9 Rangkaian untuk memperlihatkan energi yang tersimpan dalam rangkaian gandeng
maka Persamaan (7.28) menjadi :
w
1
1
L1I12  L 2 I 2 2  M.I1I 2
2
2
(7.29)
maka secara umum dapat dituliskan :
w
1
1
L1i12  L 2 i 2 2 
M.i1i 2
2
2

(*)
(7.30)
dimana (*) ditentukan oleh aturan dot.
Adapun energi yang tersimpan pada rangkaian gandeng (kumparan) tidak pernah
berharga negatif. Hal ini kaena induktor adalah merupakan kmponen pasif. Ini berarti
bahwa besaran pada sisi kanan Persamaan (7.29) ini tidak akan pernah negatif (lebih
besar atau sama dengan nol) :
1
1
L1i12  L 2 i 2 2  M.i1i 2  0
2
2
(7.31)
Bilamana Persamaan (7.31) ini ditarik akarnya, dan kemudian kedua sisinya
ditambahkan dan dibagikan dengan i1i 2 L1L 2 , maka akan diperoleh :
174
L1L 2  M  0
atau :
M  L1L 2
(7.32)
maka dari Persamaan (7.32) ini terlihat bahwa harga induktansi timbal balik M tidak
akan pernah lebih besar dari induktansi diri L1 dan L2, dan adapun batas limit / harga
yang paling besar dari M dinyatakan dengan :
k
M
L1L 2
(7.33)
atau :
M  k L1L 2
(7.34)
dimana k disebut sebagai koefisien gandeng k (coefficient of coupling k) dari kumparan
yang harganya adalah 0  k  1 atau ekivalen dengan 0  k  L1L 2 .
Koefisien gandeng ini adalah perbandingan antara fluksi yang merambat ke suatu
kumparan dengan fluksi total dari kumparan itu sendiri, sehingga dapat dituliskan
dengan:

12
k  12 
1
 22   21
(7.35)

 21
k  21 
2
 22   21
(7.36)
atau :
dengan demikian dapat dikatakan bahwa :
Koefisien gandeng adalah ukuran dari kemampuan gandeng magnetik antara
dua kumparan. 0  k  1
Contoh :
Suatu rangkaian gandeng magnetik seperti di bawah ini :
175
Carilah bentuk persamaan tegangan pada rangkaian gandeng di atas dalam wawasan
waktu dan wawasan frekuensi.
Jawab :
Rangkaian sperti di atas adalah rangkaian dalam wawasan waktu, maka manurut
hukum tegangan Kirchhoff, persamaan tegangan pada :
Loop 1 :
v1  R 1i1  L1
di1
di
M 2
dt
dt
Loop 2 :
v 2  R 2i 2  L 2
di 2
di
M 1
dt
dt
Dalam wawasan frekuensi, rangkaiannya adalah :
Rangkaian seperti di atas adalah rangkaian dalam wawasan frekuensi, maka
menurut hukum tegangan Khirchoff, persamaan tegangan pada :
Loop 1 :
V1 = R1I1 + jωL1I1 + JωMI2 = ( R1 + JωL1 ) I1 + JωMI2
Loop 2 :
V2 = JωMI1 + R2I2 + jωL2I2 = JωMI1 + ( R2 + JωL2 ) I2
Contoh :
Hitunglah berapa besar arus phasor I1 dan I2 pada rangkaian di bawah ini :
176
Jawab :
Persamaan tegangan pada loop 1 :
V  jX L1I1  jX C I1  jX M I 2 atau V  ( jX L1  jX C )I1  jX M I 2
atau :
120  ( j5  j4).I1  j3.I 2  j1 .I1  J 3 .I 2
atau :
120  190.I1  390.I 2
atau :
I2 
190.I1 120

390
390
atau :
I 2  0,3330.I1  4  90
(a)
Persamaan tegangan pada loop 2 :
0   jX M I1  R.I 2  jX L 2 I 2 atau 0   jX M I1  (R  jX L 2 ).I 2
atau :
0   j3.I1  (12  j6).I 2 atau 0  3  90.I1  13,4126,56.I 2
atau :
I2 
3  90.I1
 0.223  116,56.I1
 13,4126,56
(b)
Persamaan (a) = (b), maka diperoleh :
I 2  0,3330.I1  4  90  0.223  116,56.I1
atau :
0,3330.I1  0.223  116,56.I1  4  90
atau :
0,333.I1  (0,099  j0,199).I1  4  90
atau :
(0,234.I1  j0,199).I1  4  90
atau :
0,307  40,37.I1  4  90
atau :
I1 
4  90
 13,029  49,63 A
0,307  40,37
177
kemudian harga I1 yang diperoleh, disubstitusikan ke Persamaan (a) :
I 2  0,3330.(13,029  49,63)  4  90
atau :
I 2  4,338  49,63  j4
atau :
I 2  2,809  j3,305  j4
atau :
I 2  2,809  j0,695
atau :
I 2  2,8913,89 A
Contoh :
Perhatikan rangkaian di bawah ini :
Carilah harga k dan energi yang tersimpan dalam rangkaian gandeng ini selama 1 detik.
Jawab :
Besar konstanta gandeng k adalah :
k
M
L1 .L 2

2,5
5x 4
 0,56
Untuk mencari energi yang tersimpan dalam rangkaian gandeng ini, maka semua
besaran yang ada dalam rangkaian harus besaran wawasan frekuensi.
Disini ω = 4 rad/det
Wawasan Waktu
Wawasan Frekuensi
60 cos (4t + 30o)
60 30 o
L1 = 5 H
j ωL1 = j 20 Ω
L2 = 4 H
j ωL2 = j16 Ω
C = 0,0625 F
1/j ωC = -j4 Ω
178
R = 10 Ω
R = 10 Ω
j ωM = j10 Ω
M = 2,5 H
Maka rangkaian dalam wawasan frekuensi adalah :
Persamaan Loop 1 :
V  (R  jL1 ).I1  jM.I 2
atau :
(10  j20).I1  j10.I 2  6030
(*)
Persamaan Loop 2 :
jM.I1  ( jL 2  jC).I 2  0
atau :
j10.I1  ( j16  j4).I 2  0
atau :
j10.I1  j12.I 2  0
atau :
I1 
 j12.I 2
j10
 atau : I1  1,2.I 2
(**)
Kemudian Persamaan (**) disubstitusikan ke (*) :
(10  j20).(1,2.I 2 )  j10.I 2  6030
atau :
(12  j14).I 2  j10.I 2  6030
atau :
(12  j4).I 2  6030
atau :
I2 
6030
6030

 3,255160,6 A
(12  j4) 18,432  130,6
Harga I2 yang diperoleh disubstitusikan ke Persamaan (**) :
I1  1,2.(3,255160,6)  3,904160,6
179
atau :
I1  (3,682  j1,296)  3,682  j1,296  3,903  19,39 A
Dalam wawasan waktu (time domain), maka :
i1  3,903 cos (4t  19,39) A dan i 2  3,255 cos (4t  160,6) A
Untuk : t = 1 detik → maka : 4t = 4 rad.= 4 x 57,3o = 229,2o
sehingga :
i1  3,903 cos (229,2  19,39)  3,903 cos (209,81)  3,386 A
i 2  3,255 cos (229,2  160,6)  3,225 cos (389,8)  2,824 A
sehingga total energi yang tersimpan pada rangkaian gandeng ini :
w
1
1
L1i12  L 2 i 2 2  Mi1i 2
2
2
atau :
w
1
1
(5)(3,386) 2  (4)(2,824) 2  (2,5)(3,386)(2,824)
2
2
atau :
w  28,662  15,949  23,905  20,706 J
7.5 Transformasi Linier
Transformator adalah suatu peralatan listrik yang menggunakan fenomena dari
induktansi timbal balik, dimana pada umumnya transformator memiliki empat terminal
yang terdiri dari dua atau lebih kumparan, sebagai ilustrasi perhatikan rangkaian di
bawah ini :
Gambar 7.10 Transformator linier
180
Kumparan N1 yang langsung dihubungkan ke sumber tegangan disebut sebagai
kumparan primer, sedangkan kumparan N2 yang dihubungkan ke beban ZL disebut
sebagai kumparan sekunder, sedangkan R1 dan R2 menyatakan rugi-rugi disipasi daya
pada kumparan-kumparan.
Suatu transformator dikatakan linier, apabila kumparan-kumparan dililitkan pada
material magnet yang linier (material yang memiliki permebilitas magnet yang konstan,
misalnya udara, bakelit, kayu, plastik dan lainnya). Transformator linier ini juga sering
disebut dengan transformator dengan inti udara (air-core transformers), yang banyak
dipergunakan pada pesawat televisi dan radio.
Perlu dicari impedansi input [Zin] yang dilihat dari sisi sumber, karena impedansi
input ini mempengaruhi sifat dari rangkaian primer. Selanjutnya perhatikan Gambar
7.10, maka menurut hukum tegangan Khirchhoff dapat dituliskan :
V  (R  jL1 ).I1  jM.I 2
(7.37)
0   jL1.I1  (R 2  jL 2  Z L ).I 2
(7.38)
Dari Persamaan (7.38) didapat :
I2 
jL1.I1
(R 2  jL 2  Z L )
(7.39)
Persamaan (7.39) ini disubstitusikan ke Persamaan (7.37), maka diperoleh :
V  (R  jL1 ).I1  jM.
jL1.I1
(R 2  jL 2  Z L )
atau :
V  (R  jL1 ).I1 
 2 M 2 I1
(R 2  jL 2  Z L )
atau :


2 M 2
.I1
V   (R  jL1 ) 


(
R

j

L

Z
)
2
2
L


maka diperoleh :
Zin 
V
2 M 2
 (R  jL1 ) 
I1  (R 2  jL 2  Z L )




(1)
(2 )
(7.40)
Terlihat dari Persamaan (7.40) terbagi menjadi dua bagian, dimana bagian (1)
merupakan impedansi primer, sedangkan bagian (2) menyatakan adanya kopling antara
181
belitan primer dan sekunder dan ini menyatakan seolah-olah impedansi ini direpleksikan
ke sisi primer, sehingga impedansi ini sering disebut dengan impedansi refleksi (relected
impedance) ZR :
ZR 
2 M 2
(R 2  jL 2  Z L )
(7.41)
Terlihat dari Persamaan (7.40) dan (7.41) bahwa penempatan tanda dot tidak
berpengaruh pada suatu transformator, karena hasilnya akan sama dengan menempatkan
M ataupun –M.
7.6 Rangkaian Ekivalen Transformator Linier
Ada saatnya diperlukan rangkaian ekivalen yang menggantikan gandeng secara
magnetik dengan rangkaian yang terhubung langsung (non magnetik), yang dapat dibuat
rangkaian ekivalennya dalam hubungan T atau П seperti di bawah ini :
Gambar 7.11 Transformator linier (a) Rangkaian ekivalen ; (b) Hubungan “T” ; (c) Hubungan “П”
Dari Gambar 7.11a, adalah rangkaian tergandeng secara magnetik, dan dapat
dituliskan persamaan tegangan pada setiap loop, yaitu :
182
V1  jL1I1  jMI 2
(7.42)
V2  jMI1  jL 2 I 2
(7.43)
Persamaan (7.42) dan (7.43) ini dapat disusun dalam bentuk matrik sebagai berikut
 V1   jL1
V    jM
 2 
jM   I1 
jL 2  I 2 
(7.44)
dari Persamaan (7.42) dapat diturunkan :
V  jMI 2
I1  1
jL1
(7.45)
dari Persamaan (7.43) dapat pula diturunkan :
I1 
V2  jL 2 I 2
jM
(7.46)
kemudian samakan Persamaan (7.45) dengan Persamaan (7.46), sehingga :
V1  jMI 2 V2  jL 2 I 2

jL1
jM
atau :
(V1  jMI 2 )( jM)  (V2  jL 2 I 2 )( jL1 )
atau :
jMV1   2 M 2 I 2  jL1V2   2 L1L 2 I 2
atau :
 2 M 2 I 2   2 L1L 2 I 2  jL1V2  jMV1
atau :
I2 
jL1V2  jMV1
2
2
2
 M   L1L 2

jL1V2
2
2

2
 M   L1L 2
jMV1
2
 M 2   2 L1L 2
atau :




jL1
jM
V 
V
I2  
2
 2 M 2  2 L L 
  2 M 2  2 L L  1

1 2

1 2
atau :

jL1
I2   
  L1L 2  M 2




jM
 V2  
 V1

 (L1L 2  M 2 ) 

atau :



jL1
jM
I2  
V1  

2
 (L1L 2  M ) 
  L1L 2  M 2


 V2


atau :
183



L1
M
I2  
V1  

2
 j(L1L 2  M ) 
 j L1L 2  M 2


 V2


(7.47)
Persamaan (7.46) dapat disusun dengan bentuk :
I1 
V2
jL 2 I 2

j M
j M
kemudian Persamaan (7.47) disubstitusikan ke persamaan I1 di atas, sehingga diperoleh :
I1 
 jL
V2
2

jM  jM


 MV1
L1V2


2
 j(L1L 2  M ) j L1L 2  M 2





atau :
I1 
 jL
V2
2

jM  jM

 L1V2  MV1 


 j(L1L 2  M 2 ) 
atau :
I1 
 jL
V2
2

jM  jM



L1V2
MV1



 j L1L 2  M 2
j(L1L 2  M 2 ) 
I1 


V2
jL 2 L1V2
jL 2 MV1



jM    2 M L1L 2  M 2  2 M(L1L 2  M 2 ) 


atau :


atau :
I1 

V2
jL 2 MV1
jL 2 L1V2


2
2
2
jM   M(L1L 2  M )  M L1L 2  M 2





atau :
I1 
V2
 jL MV1  L 2 L1V2 
 2

jM  M(L1L 2  M 2 ) 
atau :
I1 
V2 M ( L1L 2  M 2 )  M( L 2 MV1  L 2 L1V2 )
j 2 M 2 ( L1L 2  M 2 )
atau :
I1 
V2 ML1L 2  V2 M 3  L 2 M 2 V1  L1L 2 MV2
j 2 M 2 ( L1L 2  M 2 )
atau :
I1 
L 2 M 2 V1  V2 M 3
j 2 M 2 ( L1L 2  M 2 )

M 2 ( L 2 V1  MV2 )
j 2 M 2 ( L1L 2  M 2 )
atau :
184
I1 
L2
2
j( L1L 2  M )
V1 
M
j( L1L 2  M 2 )
V2
(7.48)
Sehingga Persamaan (7.47) dan (7.48) disusun dalam bentuk matrik adalah :
L2


 I1   j(L1L 2  M 2 )
I   
M
 2

2
 j(L1L 2  M )
M


j(L1L 2  M 2 )   V1 
L1
 V2 

j(L1L 2  M 2 ) 
(7.49)
Adapun persamaan tegangan pada Gambar 7.11b, dapat dituliskan sebagai :
Persamaan tegangan pada loop 1 adalah :
V1  j(L a  L b )I1  jMI 2
(7.50)
Persamaan tegangan pada loop 2 adalah :
V2  jMI1  j(L b  L c )I 2
(7.51)
bila disusun dalam bentuk matrik :
 V1   j(L a  L b )
V   
jL c
 2 
jL c
  I1 
j(L b  L c ) I 2 
(7.52)
Maka dikatakan rangkaian Gambar7 11.a memiliki rangkaian ekivalen hubungan
T, bilamana persamaan (7.46) identik dengan persamaan (7.52), hal ini hanya bisa
terpenuhi apabila harga-harga :
L a  L1  M
Lc  M
Lb  L2  M





(7.53)
Selanjutnya untuk rangkaian ekivalen hubungan Π (delta) berlaku hubungan
sebagai berikut :
(lihat Gambar 7.11c). Dengan menggunakan metode tegangan simpul maka diperoleh :
 1
1 



 I1   jL A jL C 
I    
1 
 2

  
  jL C 

1  
 
 
j

L
C

  V1 
 
 1
1  V2 



 jL B jL C 
(7.54)
185
Maka dengan menyamakan matrik admitansi dari Persamaan (7.49) dan (7.54),
maka diperoleh :
L L  M2
LA  1 2
L2  M
L L  M2
LB  1 2
L1  M
L1L 2  M 2
LC 
M











(7.55)
Contoh :
Dari rangkaian dibawah ini carilah besar impedansi input dan arus I1
Jawab :
Adapun besar impedansi input :
Zin  Z1  jXL1 
2 M 2
52
 (60  j100)  j20 
Z2  ZL
(30  j40)  (80  j60)
atau :
Zin  (60  j80) 
25
25
 (60  j80) 
(110  j100)
148,6642,27
atau :
Zin  (60  j80)  0,168  42,27  (60  j80)  (0,009  j0,167)
atau :
Zin  (59,991  j79,833)  99,86  53,07 
186
maka besar arus input :
I1 
V1
5060

 0,5113,07 A
Z in 99,86  53,07
Contoh :
Buatlah rangkaian ekivalen hubungan T dari transformator linear dibawah ini :
Jawab :
Dalam hubungan T berlaku :
L a  L1  M  10  2  8 H
Lc  M  2 H
Lb  L2  M  4  2  2 H
maka rangkaian ekivalennya :
Contoh :
Carilah rangkaian ekivalen hubungan Π dari rangkaian transformator linear
dibawah ini :
187
Jawab :
Dalam hal ini :
L L  M 2 10.4  2 2
LA  1 2

 18 H
L2  M
42
L L  M 2 10.4  2 2
LB  1 2

 4,5 H
L1  M
10  2
L L  M 2 10.4  2 2
LC  1 2

 18 H
M
2
Rangkaian ekivalennya adalah :
7.7 Tranformator Ideal
Tranformator ideal adalah suatu peralatan yang memiliki
harga koefisien
gandeng k = 1 yang terdiri dari dua atau lebih kumparan dengan jumlah belitan yang
banyak yang dililitkan pada inti dari bahan yang memiliki permeabilitas yang tinggi,
yang mana hal ini menyebabkan semua fluksi akan melingkupi seluruh kumparan.
Untuk memperlihatkan suatu transformator ideal (yang terdiri dari dua kumparan)
dimana besar induktansi-nya mendekati tak terhingga dan koefisien gandeng k = 1, maka
perhatian rangkaian pada Gambar 7.12. dibawah ini :
188
Gambar 7.12 Transformator ideal
Adapun persamaan tegangan dari rangkaian diatas adalah :
V1  jL1I1  jMI 2
(7.56)
V2  jMI1  jL 2 I 2
(7.57)
Dari persamaan (7.56) diperoleh :
I1 
(V1  jMI 2 )
jL1
dan apabila harga I1 ini disubtitusikan kedalam Persamaan (7.57) akan diperoleh :
(V1  jMI 2 )
(V1M  jM 2 I 2 )
V2  jM
 jL 2 I 2 
 jL 2 I 2
jL1
L1
atau :
V M jM 2 I 2
V2  jL 2 I 2  1 
L1
L1
L1.L 2 , sehingga ;
akan tetapi untuk K = 1, menurut Persamaan (7.34) harga M =
V L .L
jL1L 2 I 2
V2  jL 2 I 2  1 1 2 
L1
L1
atau :
V L .L
V2  1 1 2 
L1
bila dimisalkan M =
V1
L12 L 2
L1
L1
V1L1

L1
L2
L1
 V1
L2
L1
L1 / L 2 , yang disebut sebagai perbandingan belitan, sehingga
persamaan diatas berbentuk :
V2 = nV1
189
Maka bilamana L1: L2; M  ∞ maka harga dan akan tetap, sehingga rangkaian gandeng
disebut sebagai suatu tranformator ideal. Adapun sifat-sifat dari suatu transformator ideal
diantaranya adalah :
1. Kumparannya memiliki harga reaktansi yang sangat besar (L1; L2;M ∞)
2. Koefensi gandeng k = 1
3. Kumparan primer dan sekundur tanpa rugi-rugi (R1 = 0 = R2)
dimana tranformator ideal dapat digambarkan seperti Gambar 7.13 di bawah ini :
N1
N2
Gambar 7.13 Transformator ideal
dan tranformator ideal ini sering disimbolkan seperti Gambar 7.14 berikut ini.
Gambar 7.14 Simbol transformator ideal
Bilamana pada sisi primer dari suatu tranformator ideal diberikan sumber
tegangan sinusoidal V seperti pada Gambar 7.15 dibawah ini.
190
Gambar 7.15 Transformator ideal dengan sumber tegangan ac pada sisi primer
Maka pada kedua belitan akan muncul fluksi dan menurut Hukum Faraday tegangan
yang terjadi pada belitan primer adalah :
v1  N1
d
dt
(7.58)
Dan pada belitan sekunder :
v2  N2
d
dt
(7.59)
kemudian bagikan Persamaan (7.59) dengan Persamaan (7.58) maka diperoleh :
v2 N2

n
v1 N1
(7.60)
dimana n disebut sebagai perbandingan belitan atau perbandingan tranformasi, dimana
lebih sering digunakan tegangan phasor V1 dan V2 dari pada tegangan sesaat v1 dan v2
sehingga Persamaan (60) menjadi :
V2 N 2

n
V1 N1
(7.61)
Sesuai dengan prinsip konversi energi, maka energi yang diberikan pada sisi
primer harus sama dengan energi yang diabsorbsi siis sekunder sehingga tidak ada rugirugi yang terjadi dan hal ini adalah salah satu sifat dari tranformato ideal, sehingga
dengan demikian dapat dituliskan :
v1i1  v 2i 2
(7.62)
dalam bentuk phasor bila Persamaan (7.62) di konjugasikan dengan Persamaan (7.61)
diperoleh :
I1 V2

n
I 2 V1
(7.63)
191
Terlihat bahwa arus-arus pada sisi primer dan sekunder bila dihubungkan dengan
perbandingan belian n dapat dilakukan dengan cara mengambil inverse perbandingan
tegangan. Adapun Persamaan (7.61) dapat dinyatakan dengan :
V1 N1 1


V2 N 2 n
(7.64)
demikian pula Persamaan (7.63) dapat dinyatakan dengan :
V1 I 2 1


V2 I1 n
(7.65)
bilamana Persamaan (7.64) diperbandingkan dengan Persamaan (7.65) maka dapat
dinyatakan :
I 2 N1 1


I1 N 2 n
(7.66)
dilihat dari Persamaan (7.66) maka :
1. Bilamana n = 1 :
Maka tranformator dikatakan sebagai transformator isolasi (isolation tranformer)
2. Bilamana n > 1 :
Tranformator
dikatakan
sebagai
tranformator
penaik
tegangan
(step-up
transformator), disini tegangan pada sisi primer dinaikan pada sisi sekunder (V2>V1)
3. Bilamana n < 1 :
Tranformator dikatakan
sebagai transformator penurun tegangan (step-down
tranformer), disini tegangan pada sisi primer diturunkan pada sisi sekunder (V2<V1)
Bila dilihat dari Persamaan (7.61) dan (7.66) maka selalu dapat diekspresikan V1
dalam V2 dan II dalam I2 atau sebaliknya sehingga :
V1 
V2
n
(7.67)
atau :
V2  nV1
(7.68)
I1  nI 2
(7.69)
demikian pula halnya dengan :
atau :
192
I
I2  1
n
(7.70)
Satu hal yang penting adalah bagaiamana untuk mengetahui poloritas dari
tegangan ataupun arah arus dalam suatu transformator seperti pada Gambar 7.15. Kalau
polaritas V1 ataupun V2 dan arah I1 ataupun I2 dirubah, maka n pada Persamaan (7.61)
sampai dengan Persamaan (7.66) tanda aljabarnya diganti menjadi –n.
Sebagai lengkapnya dapat diperlihatkan seperti Gambar 7.16 dibawah ini :
Gambar 7.16 Untuk menentukan polaritas tegangan dan arah arus pada transformator ideal
Sehingga dapat disimpulkan :
1. Bilamana tegangan kumparan V1 dan V2 kedua-duanya positif atau negatif pada
terminal dot, maka pergunakan tanda-tanda +n pada Persamaan (7.61), kalau tidak
gunakan tanda
–n.
2. Bilamana arus-arus I1 dan I2 kedua-duanya menuju atau meninggalkan terminal dot,
maka pergunakan tanda -n pada Persamaan (7.66), kalau tidak gunakan tanda +n.
Selanjutnya adapun daya kompleks pada sisi primer dinyatakan dengan :
193
S1  V1I* 
V2
(nI 2 )*  V2 I 2 *  S 2
n
terlihat bahwa daya kompleks diberikan dari sisi ke sisi sekunder tanpa rugi-rugi, hal ini
terjadi karena yang sedang ditinjau adalah tranformator ideal yang bersifat rugi-rugi.
Adapun impedansi input dapat ditentukan dengan memperhatikan rangkaian pada
Gambar 7.17 dibawah ini :
Gambar 7.17 Rangkaian untuk menyatakan impedansi input Zin
dari Persamaan (7.67); (7.68); (7.69) dan (7.70) diperoleh :
V
1 V2
Zin  1 
.
I1 n 2 I 2
(7.71)
kemudian dari Gambar 7.17 juga terlihat bahwa : ZL = V2/I2, dengan demikian
Persamaan (7.71) menjadi :
Zin 
ZL
n2
(7.72)
Biasanya salah satu spesifikasi dari suatu transformator dinyatakan dengan V1/V2,
misalnya suatu tranformator dengan spesifikasi 2400/120 volt [rms], maka ini berarti
pada sisi primer adalah 2400 volt [rms] dan tegangan pada sisi sekunder 120 vol [rms]
sehingga tranformator ini merupakan tranformator penurun tegangan (step-down
tranformer).
Contoh :
Sebuah tranfomator ideal dengan data-data : 2400/120 vol; 9,6 kVA dimana jumlah
belitan pada sisi sekunder 50 lilitan. Hitunglah :
a. Perbandingan belitan n
b. Banyak belitan pada sisi primer
194
c. Arus primer dan sekunder (I1 dan I2)
Jawab :
Tranformator ini adalah tranformator penurun tegangan (step-down transformer)
dimana tegangan pada sisi primer V1 = 2400 volt dan tegangan pada sisi sekunder
V2 = 120 volt. Maka :
a. Perbandingan belitan adalah :
n
V2
120

 0,05
V1 2400
b. Banyak belitan pada sisi primer :
n
N2
N1
atau :
N1 
N2
50

 1000
n
0,05
liltan
c. Daya semu tranformator adalah :
S  V1I1  V2 I 2  9,6 kVA
maka :
I1 
S
9600

 4 Amp.
V1 2400
dan :
I2 
S
9600

 80 Amp.
V2
120
Contoh :
Suatu tranformator ideal seperti rangkaian dibawah ini.
Hitunglah :
195
a. Besar arus I1 yang disuplai oleh sumber.
b. Besar tegangan output V0
c. Daya kompleks yang disuplai oleh sumber
Jawab :
a. Tahanan R2 dapat direfleksikan ke sisi primer
ZR 
R2
n
2

20
22
5
sehingga :
Zin  (R 1  jX C )  Z R  (4  j6)  5  (9  j6)
atau :
Zin  10,82  33,69 
maka :
I1 
V
1200

 11,0933,69 Amp.
Z in 10,82  33,69
b. Karena arus I1 dan I2 meninggalkan tanda dot, maka
I2  
1
1
I1   (11,0933,69)  5,54533,69 Amp .
n
2
c. Adapun daya kompleks yang disuplai oleh sumber :
S  V.I1*  (1200)(11,09  33,69)  1330,8  33,69 VA
7.8 Autotranformator Ideal
Autotranformator adalah sebuah tranformator dimana bagian primer dan
sekunder-nya dalam satu belitan dengan sebuah terminal diantara sisi primer dan
sekunder (selalu disebut dengan tap).
Beberapa rumus dalam
transformator
ideal juga
dipergunakan
dalam
autotranformator, misalnya untuk autotranformator penurun tegangan seperti pada
Gambar 7.18 dibawah ini.
196
Gambar 7.18 Autotransformator penurun tegangan
Dari persamaan (7.61) maka untuk autotranformator penurun tegangan ini
berlaku :
V1 N1  N 2
N

 1 1
V2
N2
N2
(7.73)
karena pada autotranformator ideal ini juga tidak ada rugi-rugi, maka daya kompleks
pada sisi belitan primer sama dengan sisi belitan sekunder, sehingga :
S1  V1I1*  S 2  V2 I 2 *
(7.74)
sehingga dari Persamaan (7.74) ini dapat pula dinyatakan bahwa :
V1I1  V2 I 2
atau :
V2 I1

V1 I 2
(7.75)
maka hubungan antara arus dapat dinyatakan dengan :
I1
N2

I 2 N1  N 2
(7.76)
Untuk autotranformator ideal penaik tegangan seperti Gambar 7.19, dibawah ini :
197
Gambar 7.19 Autotransformator penaik tegangan
Untuk autotranformator penaik tegangan ini berlaku :
V1
V2

N1 N1  N 2
atau :
V1
N1

V2 N1  N 2
(7.77)
Sedangkan untuk daya komplek pada autotranformator penaik tegangan ini berlaku
Persamaan (7.74).
Adapun
perbedaan
yang
utama
antara
transformator
ideal
dengan
autotranformator ideal ini adalah pada autotranformator sisi primer dan sekunder selain
terhubung secara magnetik juga terhubung konduktif.
Contoh :
Dari rangkaian autotranformator dibawah ini :
Hitunglah besar : a. I1, I2 dan Io
b. Daya kompleks yang disuplai ke beban ZL
Jawab :
a. Autotranformator adalah penaik tegangan sehingga berlaku :
V1
N1
80
80



V2 N1  N 2 80  120 200
atau :
198
V2 
200
200
V1 
(12030)  300 30 volt
80
80
dari rangkaian terlihat bahwa :
I2 
V2 30030
30030


 30  6,87 Amp.
ZL
(8  j6) 1036,87
kemudian dari rumus :
I1 N1  N 2 80  120 200



I2
N1
80
80
atau :
I1 
200
200
I2 
(30  6,87)  75  6,87 Amp .
80
80
Menurut hukum arus Kirchoff pada titik tap persamaannya adalah ;
I 2  I1  I o
atau :
I o  I 2  I1  (30  6,87)  (75  6,87)  ( 29,78  j3,58)  (74,46  j8,97)
sehingga :
I o  44,68  j5,39  45173,12 Amp.
b. Adapun daya kompleks yang disuplai ke beban adalah :
S 2  V2 I 2 *  I 2 Z L  30 2 (1036,87)  900036,87  936,87 kVA
7.9 Soal Latihan
1. Dua buah kumparan yang tergandeng secara magnetik dengan koefisien gandeng
k = 0,85 dimana kumparan N1 memiliki 250 belitan yang dialiri arus i1 = 2 A dengan
fluksi total φ1 = 0,3 mWb. Bila arus i1 tereduksi secara linier ke harga nol dalam
waktu 2 milli detik maka tegangan yang terinduksi pada kumparan N2 sebesar
63,75 V. Hitunglah L1 ; L2 ; M dan N2.
2. Dua buah kumparan yang tergandeng secara magnetik dengan N1 = 100 lilitan dan
N2 = 800 lilitan mempunyai koefisien gandeng k = 0,85. Dengan lilitan N1 terbuka
199
maka arus yang mengalir pada lilitan N2 sebesar 5 A dan fluksi φ2 = 0,35 mWb.
Hitunglah berapa besar L1 ; L2 dan M.
3. Pada rangkaian di bawah ini, hitunglah perbandingan V2/V1 yang mengakibatkan
arus I1 = 0.
4. Pada rangkaian di bawah ini, hitunglah berapa besar harga koefisien gandeng k
bilamana disipasi daya pada R sebesar 32 watt.
V  200 V
5. Hitunglah impedansi input dari rangkaian berikut.
XL1 = 4 Ω
R=3Ω
XM = 3 Ω
V
I1
XL2 = 5 Ω
I2
Xc = 8 Ω
6. Dari rangkaian transformator ideal di bawah ini hitunglah besar Vo dan daya
kompleks yang diberikan oleh sumber.
V  100 0 V (rms )
7. Hitunglah daya yang diberikan sumber pada R2 pada rangkaian di bawah ini.
200
V  1000 V( rms)
8. Pada rangkaian di bawah ini L3 tidak tergandeng secara magnetik dengan L1 dan L2.
Maka hitunglah I1 ; I2 dan Is untuk ω = 1000 rad/detik.
9. Pada rangkaian autotransformator di bawah ini hitunglah VL ; IL dan Icb.
201
V  150 0  V
Z L  1060 
202