A. FLUIDA STATIS Teori Singkat : Fluida adalah zat yang dapat

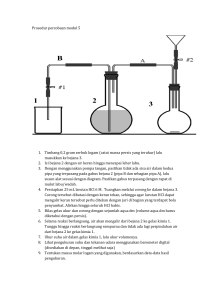
A. FLUIDA STATIS
 Teori Singkat :
Fluida adalah zat yang dapat mengalir atau
sering disebut Zat Alir. Fluida dapat mencakup
zat cair atau gas.
Zat cair : adalah Fluida yang non kompresibel
(tidak dapat ditekan) artinya tidak berubah
volumenya jika mendapat tekanan.
Gas : adalah fluida yang kompresibel, artinya
dapat ditekan.
Bagian fisika yang mempelajari tekanantekanan dan gaya-gaya dalam zat cair disebut:
Hidrolika atau Mekanika Fluida yang dapat
dibedakan dalam :
a) Hidrostatika : Mempelajari tentang gaya
maupun tekanan di dalam zat cair yang
diam.
b) Hidrodinamika : Mempelajari gaya-gaya
maupun tekanan di dalam zat cair yang
bergerak (mekanika fluida bergerak)
1. Rapat Massa dan Berat Jenis
Rapat massa / massa jenis benda-benda
homogen biasa didefinisikan sebagai : massa
persatuan volume yang disimbolkan dengan .
= m
V
Berat jenis didefinisikan sebagai berat
persatuan volume, dengan simbol s :
s
w mg

 g
V
V
2. Tekanan Hidrostatika
Tekanan Hidrostatika adalah tekanan yang
disebabkan oleh berat zat cair.
Tekanan adalah : Gaya per satuan luas yang
bekerja dalam arah tegak lurus suatu
permukaan.
P= F
A
Tiap titik di dalam fluida tidak memiliki
tekanan yang sama besar, tetapi berbeda-beda
sesuai dengan ketinggian titik tersebut dari
suatu titik acuan.
Pbar
h
P = Pbar +
Dasar
bejana
akan
mendapat tekanan sebesar
: P = tekanan udara luar +
tekanan oleh gaya berat
zat
cair
(Tekanan
Hidrostatika).
Gaya berat fluida
Luas penampang dasar bejana
P = Pbar +
ρ.v.g
ρ.g.A.h
= Pbar +
A
A
Jadi Tekanan Hidrostatika (Ph) didefinisikan :
Ph =  . g . h
Sehingga P = Pbar + Ph
 Catatan :
1 atm = 76 cm Hg
1 atm = 105 N/m2 = 106 dyne/cm2
1 Pa (=Pascal) = 1 N/m2
Pbar = Tekanan udara luar
3. Gaya Hidrostatika (= Fh)
Besarnya gaya hidrostatika (Fh) yang bekerja
pada bidang seluas A adalah :
Fh = Ph . A =  . g . h . A
Fh =  . g . h . A
4. Hukum Pascal
"Tekanan yang bekerja pada fluida di dalam
ruang tertutup akan diteruskan oleh fluida
tersebut ke segala arah dengan sama besar".
Contoh alat yang berdasarkan hukum Pascal
adalah : Pompa Hidrolik.
Perhatikan gambar bejana berhubungan di
bawah ini.
F1
F2
A1
A2
Permukaan fluida pada kedua kaki bejana
berhubungan sama tinggi. Bila kaki I yang luas
penampangnya A1 mendapat gaya F1 dan kaki
II yang luas penampangnya A2 mendapat gaya
F2 maka menurut Hukum Pascal harus berlaku :
P1 = P2
F1  F2
A1 A2
5. Hukum Utama Hidrostatis
"Tekanan hidrostatis pada sembarang titik
yang terletak pada bidang mendatar di dalam
sejenis zat cair yang dalam keadaan setimbang
adalah sama".
Hukum utama hidrostatika berlaku pula pada
pipa U (Bejana berhubungan) yang diisi lebih
dari satu macam zat cair yang tidak bercampur
1
h1
h2
A
B
Jika benda diletakkan di dalam zat cair, maka
akan memiliki 4 macam keadaan :
1. Benda tenggelam
FA = ρc g V
W = ρb g V
(Ph)A = (Ph)B → 1 g h1 = 2 g h2
Dari gambar disamping
tampak :
W > FA
1 h1 = 2 h2
Percobaan pipa U ini biasanya digunakan untuk
menentukan massa jenis zat cair.
6. Paradoks Hidrostatis
"Gaya hidrostatis pada dasar bejana tidak
tergantung pada banyaknya zat cair maupun
bentuk bejana, melainkan tergantung pada :
Massa jenis zat cair, tinggi zat cair diatas
dasar bejana dan luas dasar bejana".
Untuk bejana yang mempunyai luas dasar
(A) yang sama dan berisi zat cair dengan
ketinggian yang sama pula (h), menurut hukum
utama hidrostatis : Tekanan hidrostatis pada
dasar masing-masing bejana adalah sama yaitu :
Ph =  . g . h dan karena Fh = Ph A, maka :
W FA
Sehingga
2. Benda melayang
FA w
Sehingga
w
Berat semu benda di dalam zat cair
FA
Wc
Wu
Wu = Wc + FA
# Wc = Berat benda di dalam zat cair (N)
# Wu = Berat benda di udara (N)
# FA = Gaya Archimedes (N)
F A = ρc g V
# ρc = Massa jenis zat cair (kg/m3)
ρb = ρc
Vter.#Vter. = Volume terapung
#Vterc.= Volume tercelup
Vterc.
# Vb = Volume benda
Vb = Vter. + Vterc.
W = FA → ρb g Vb = ρc g Vterc.
ρb Vb = ρb Vterc.
4. Benda terapung seluruhnya
w
FA
Dari gambar disamping
tampak :
W = FA
3. Benda terapung sebagian
Fh =  . g . h . A
7. Hukum Archimedes
"Bila sebuah benda diletakkan di dalam fluida,
maka fluida tersebut akan memberikan gaya ke
atas (FA) pada benda tersebut yang besarnya =
berat fluida yang dipindahkan oleh benda
tersebu".
ρb > ρc
FA
Dari gambar disamping
tampak :
W< FA
Sehingga ρb < ρc
8. Kohesi dan Adhesi
Kohesi : adalah gaya tarik menarik antara
partikel-partikel suatu zat yang sejenis.
Misalnya : gaya tarik menarik yang terjadi pada
air, besi dan sebagainya.
Makin kuat kohesi ini, makin kuat bendanya
(tidak mudah berubah bentuknya).
Berarti kohesi molekul-molekul zat padat lebih
besar dari kohesi molekul-molekul zat cair dan
dari kohesi molekul-molekul zat gas.
2
Adhesi : adalah gaya tarik menarik antara
partikel-partikel dari zat yang berbeda/tak
sejenis.
Contoh : Kapur tulis yang melekat pada papan.
F = Gaya yang bekerja.(N)
L = Panjang batas antara benda dengan
permukaan zat cair (m)
 = Tegangan permukaan.(N/m)
9. Pengaruh Kohesi & Adhesi Terhadap
Permukaan Fluida
Air : Permukaannya cekung, pada pipa kapiler
permukaannya lebih tinggi, karena adhesinya
lebih kuat dari kohesinya sendiri.
Air Raksa : Permukaannya cembung,
sedangkan pada pipa kapiler permukaannya
lebih rendah, karena kohesi air raksa lebih besar
dari adhesi antara air raksa dengan kaca.
 Catatan :


Air
 = Sudut Kontak.
Air Raksa
Sudut Kontak ()
Sudut kontak yaitu sudut yang dibatasi oleh 2
bidang batas dinding tabung dan permukaan zat
cair.
Dinding tabung : sebagai bidang batas antara
zat cair dan tabung.
Permukaan zat cair : Sebagai bidang batas
antara zat cair dan uapnya ( = 1800)
Bila zat cair tersebut air dan dindingnya
gelas maka :
0
0    90
1. Untuk benda berbentuk lempeng : Panjang
batasnya = kelilingnya.
2. Untuk benda berbentuk bidang kawat :
panjang batasnya = 2 x kelilingnya.
3. Untuk benda berbentuk kawat lurus, juga
pada lapisan tipis (Selaput mempunyai 2
permukaan zat cair) : panjang batasnya = 2
x Panjang (L).
11. Miniskus dan Kapilaritas
Miniskus : Yaitu bentuk permukaan zat cair
dalam suatu pipa yaitu cekung atau cembung.
Makin sempit pipa (pembuluh) makin jelas
kelengkungannya.
Kapilaritas : Yaitu suatu gejala turun atau
naiknya zat cair dalam pembuluh yang sempit,
jika pembuluh yang kedua ujungnya terbuka ini
dimasukkan tegak lurus ke dalam bak yang
berisi zat cair.
Sedang pembuluh sempit tersebut tersebut
disebut pipa kapiler.
Kenaikan/penurunan permukaan zat cair dalam
kapiler dapat dirumuskan sebagai berikut :

y
y=
2 .  . cos 
 .g.r
Karena adhesinya lebih besar dari kohesi.
Bila zat cair tersebut air raksa, maka :
900    1800
Karena kohesinya lebih besar dari adhesi.
10. Tegangan Permukaan
Sebagai akibat dari adanya kohesi zat cair
dan adhesi antara zat cair-udara diluar
permukaannya, maka pada permukaan zat cair
selalu terjadi tegangan yang disebut tegangan
permukaan.
Karena adanya tegangan permukaan inilah
nyamuk, jarum, pisau silet dapat terapung di
permukaan zat cair meskipun massa jenisnya
lebih besar dari zat cair.
Tegangan permukaan dapat dirumuskan
sebagai berikut :
= F
L
y = Kenaikan/penurunan zat cair dalam kapiler
(m)
 = Tegangan permukaan zat cair (N/m)
 = Sudut kontak
3
 = Massa jenis zat cair (kg/m )
2
g = Percepatan gravitasi (m/s )
r = Jari-jari kapiler (m)
12. Hukum Archimedes Untuk Gas
Balon Udara
Sebuah balon udara dapat naik disebabkan
adanya gaya ke atas yang dilakukan oleh udara.
Balon udara diisi dengan gas yang lebih ringan
dari udara mis : H2, He sehingga terjadi
peristiwa seolah-olah terapung.
Balon akan naik jika gaya ke atas FA>Wtot
(berat total) sehingga :
3
6πrVT = g Vb (b - f)
VT =
Fn
g Vb  b   f

6  r
Untuk benda berbentuk bola dengan jari-jari
4
r maka volume bola Vb =  r 3 sehingga
3
FA
VT =
Wtot
2 r2g
 b   f
9 

Fn = FA - Wtot
=====O0O=====
Keterangan :
FA = ud . g . Vbalon dan
Wtot = Wbalon + Wgas + Wbeban
Wgas = gas . g . Vbalon
FA = Gaya ke atas (N)
Fn = Gaya naik (N)
gas = Massa jenis gas pengisi balon
(kg/m3)
3
ud = Massa jenis udara = 1,3 kg/m
W = Berat (N)
V
= Volume (m3)
13. Hukum Stokes Untuk Fluida Kental
Jika kekentalan (viskositas) suatu fluida
tidak diabaikan, maka akan muncul gaya gesek
ke atas disamping gaya archimedes pada benda.
Gaya gesek inilah yang dikenal dengan hukum
Stokes
Ff = 6πrV
 = koefisien kekentalan (viskositas)
r = jari-jari benda berupa bola
Dari hasil percobaan diperoleh jika suatu
benda dimasukkan ke dalam suatu fluida kental,
maka kecepatan benda di dalam fluida makin
besar sampai mencapai kecepatan terbesar yang
konstan. Kecepatan yang konstan inilah yang
dinamakan kecepatan terminal (VT).
FA
Ff
arah
gerak
W = mg VT
Dari skema diatas diperoleh :
W = FA + Ff → Ff = W - FA
4
(E)
 Contoh Soal dan Pembahasan :
1. Jika percepatan gravitasi adalah 9,81 m/s2
maka berat jenis raksa dalam satuan SI,
adalah ....
(A) 13,6 kg/dm3
(B) 13,6 x 1000 x 9,81 N/m3
(C) 13,6 x 1000 kg/m3
(D) 13,6 x 981 dyne / cm3
(E) 13,6 N/m3
Jawaban : B
Massa jenis air raksa : ρ = 13,6 gr/cm3
w mg
Ingat ! s  
  g , sehingga :
V
V
s = 13,6 x 1000 x 9,81 N/m3
2. Apabila pipa barometer diganti dengan pipa
yang luas penampangnya dua kalinya maka
pada tekanan udara luar 1 atmosfer tinggi
raksa dalam pipa ....
(A) 19 cm
(D) 114 cm
(B) 38 cm
(E) 152 cm
(C) 76 cm
Jawaban : A
Gaya keatas yaitu gaya Archimedes tidak
bergantung pada kedalaman benda, tetapi
hanya bergantung pada massa jenis,
gravitasi dan volume benda : FA = ρc g V
4. Sebuah bendungan menampung air dengan
ketinggian 5 meter. Jika panjang dinding
bendungan adalah 40 meter, maka besarnya
gaya yang dibutuhkan oleh dinding untuk
menahan air adalah ....
5m
(A) 1,00 x 104 N
(B) 2,50 x 105 N
(C) 5,00 x 106 N
Jawaban : C
Tinggi permukaan air raksa dalam pipa
tidak tergantung pada luas penampang
3. Grafik di bawah ini yang menunjukkan
sehubungan gaya ke atas dengan kedalaman
benda adalah....
FA
(A)
(B)
(C)
(D)
(D) 1,00 x 107N
(E) 2,50 x 107 N
Jawaban : D
A = 5 x 40 m2 = 200 m2
Fh =  . g . h . A
= (103) (10) (5) (200) N = 1,00 x 107N
5.
h
FA
FA
air
h
Kempa hidrolik memiliki perbandingan
diameter pengisap 1 : 40. apabila pada
pengisap besar dimuati mobil 32.000 N,
agar setimbang, pada pengisap kecil diberi
gaya sebesar ....
(A) 0,1 N
(D) 0,7 N
(B) 0,3 N
(E) 1 N
(C) 0,5 N
H
Jawaban : A
D1
1

dan F2 = 32.000 N
D2 40
F1  F2 → F  A1 F .
1
2
A1 A2
A2
h
FA
5
2
2
alkohol
h2
minyak
h1
h0
air
(A) 0,1 cm
(B) 0,2 cm
(C) 0,3 cm
(D) 0,4 cm
(E) 0,5 cm
Jawaban : A
Tekanan pada tabung kiri = tekanan di
tabung kanan. Jadi P1 + P2 = P0
ρm g h1 + ρalk g h2 = ρa g (h1 + h0)
ρm h1 + ρalk h2 = ρa (h1 + h0)
(0,8)(3) + (0,7)(1) = (1) (3 + h0)
h0 = 0,1 cm
7.
zat cair
P
x = 0,4 cm
Untuk menentukan massa jenis zat cair
dirangkai alat seperti gambar di atas.
Pengisap P adalah bergerak bebas dengan
luas penampang 1 cm2. Jika konstanta pegas
100 N/m dan pegas tertekan sejauh 0,4 cm,
maka massa jenis zat cair tersebut (dalam
kg/m3) adalah ....
(A) 1000 kg/m3
(D) 500 kg/m3
3
(B) 800 kg/m
(E) 400 kg/m3
(C) 750 kg /m3
Jawaban : E



8.
6. Pada gambar diketahui massa jenis minyak
0,8 g/cm2, massa jenis alkohol = 0,7 g/cm2.
Bila tinggi h1 = 3 cm, h2= 1 cm, berapa
besar ho?
1m

Jadi
D 
 1 
F1   1  F2  F1    32000 N
 40 
 D2 
F1 = 0,5 N

kx
100 4 x10 3 kg / m 3

ghA
101 10 4
 = 400 kg/m3
2
D2
D
Dengan A = π r2 = π   = 
4
2
10 cm
10 cm
minyak
air
Dari gambar diatas, massa jenis air adalah 1
g/cm3 dan massa jenis minyak 0,8 g/cm3.
Balok kayu memiliki panjang sisi 10 cm,
dan 20% volumenya berada di dalam air.
Massa balok kayu tersebut adalah ....
(A) 440 gram
(D) 940 gram
(B) 640 gram
(E) 1040 gram
(C) 840 gram
Jawaban : C
Va = 0,2 VB ,Vm = 0,8 VB dan VB = 103 cm3
Berat benda = gaya ke atas oleh 2 jenis
cairan. Didapat : W = FAa + FAm
mg = ρa g Va + ρm g Vm
m = ρa Va + ρm Vm
m =[(1)(0,2) (103) + (0,8) (0,8)(103)] gram
m = 840 gram
9. Sebatang jarum yang panjangnya 10 cm
diletakkan
perlahan-lahan
di
atas
permukaan bensin. Jarum terapung dalam
bensin dan tepat akan tenggelam. Massa
jenis jarum ρ = 3,92 g/cm3, tegangan
permukaan bensin pada suhu tersebut γ =
0,0314 N/m. Jika  = 3,14 dan g =10 m/s2,
maka radius jarum adalah ....
(A) 34 mm
(D) 76 mm
(B) 74 mm
(D) 12 mm
(C) 75 mm
Jawaban : C
 = F → F =  L → ρ g V =  L.
L
Jika V = π r2 L, maka ρ g π r2 L =  L
3,14 x 10 2

r
r
m
 g
 3290 10 
r = 0,0005 m = 0,5 mm
1m
Fh
x = 0,4 cm
Fx
Gaya hidrostatis = gaya pegas
Fh = Fx →  g h A = k x
10. Tentukan kecepatan terminal sebuah bola
alumunium bergaris tengah 2 mm yang
jatuh ke dalam air, jika massa jenis
alumunium 2,7 x 103 kg m-3, dan koefisien
viskositas air 1,0 x 10-3 Pas (Percepatan
gravitasi = 9,8 ms-2).
(A) 11,8 m/s
(D) 14,8 m/s
(B) 12,8 m/s
(E) 15,8 m/s
6
(C) 13,8 m/s
 Soal-soal :
Jawaban : D
D = 0,5 mm → r = 1 mm
u = 1,30 kg m-3,  = 1,0 x 10-3 Pas
VT =
2 r2g
 b   f
9 



1. Grafik berikut ini yang menunjukkan
hubungan tekanan hidrostatis dengan
kedalaman adalah ....
(A) P
2 2 x10 3 9,8
2,7  110 3 m / s
VT 
-3
9 1,0 x 10
VT = 14,8 m/s
2


(B)
P
=====O0O=====
(C)
P
(D)
P
h
h
h
h
(E)
P
h
2. Tekanan hidrostatis pada kedalaman h
adalah p. Pada kedalaman 2h, tekanan
hidrostatisnya sebesar ....
(A) 0,25 p
(D) 2p
(B) 0,5 p
(E) 4p
(C) p
3. Raksa pada bejana berhubungan mempu
nyai selisih ketinggian permukaan 2 cm
(masa jenis = 13,6 g cm-3). Kaki sebelah kiri
berisi zat cair yang tingginya 25 cm, berarti
massa jenis zat cair itu adalah ....
(A) 800 kg m-3
(D) 1300 kg m-3
-3
(B) 1030 kg m
(E) 1360 kg m-3
-3
(C) 1088 kg m
4.
7
Manometer pada gambar di atas diisi
dengan raksa (rapat jenis = 13,6 g/cm3).
Beda level raksa pada kedua kaki adalah h
= 19 cm. Bila tekanan udara luar 1 x 105
N/m2 dan percepatan gravitasi = 10 m/s2,
maka tekanan gas di dalam tangki adalah ....
(A) 0,75 x 105 N/m2
(B) 1,0 x 105 N/m2
(C) 1,22 x 105 N/m2
(D) 1,24 x 105 N/m2
(E) 1,26 x 105 N/m2
5. Gaya Archimedes yang bekerja pada sebuah
benda di dalam zat cair sebanding dengan
....
(A) berat zat cair
(B) berat zat cair dan volume benda
(C) berat dan massa jenis zat cair
(D) volume benda dan massa jenis zat cair
(E) volume benda, berat zat cair, dan
massa jenis zat cair
6. Sebuah benda dapat tenggelam dalam zat
cair karena ....
(A) berat benda lebih besar dari gaya
Archimedes
(B) massa jenis benda kurang dari massa
jenis zat cair
(C) volume benda sama dengan volume
zat cair yang didesak
(D) gaya Archimedes lebih besar dari
berat benda
(E) massa jenis zat cair lebih besar dair
massa jenis benda
7. Sebuah ban dalam mobil diisi udara,
volumenya 0,1 m3 dan massanya 1 kg.
Apabila ban itu digunakan sebagai
pengapung di dalam air, massa jenis air 103
kg/m3 dan percepatan gravitasi 10 ms-2,
maka ban dapat mengapungkan beban
maksimal sebesar ....
(A) 1001 kg
(D) 100 kg
(B) 1000 kg
(E) 99 kg
(C) 101 kg
8. Sebuah balon berbentuk boal dengan
diameter 10 m berisi udara – panas.
Kerapatan udara di dalam bola adalah 75%
kerapatan udara luar (kerapatan udara luar
1,3 kg/m3). Besar massa total maksimum
penumpang dan beban yang masih dapat
diangkut balon tersebut (g=10 m/s2) adalah
....
(A) Nol
(D) 510 kg
(B) 1,3 kg
(E) 680 kg
(C) 170 kg
9. Bola besi padat yang beratnya 2,0 N
diikatkan pada sebuah kawat dan
dicelupkan dalam minyak (massa jenis 0,80
g/cm2). Bila massa jenis besi 7,9 g/cm3,
maka tegangan kawat adalah ....
(A) 2,0 N
(D) 1,2 N
(B) 1,8 N
(E) 2,2 N
(C) 1,6 N
10. Sebuah batu memiliki berat 30 N di udara
dan 21 N dalam air. Massa jenis batu
tersebut sebesar ....
(A) 9 g/cm3
(D) 1,2 N
(B) 7,8 g/cm3
(E) 0,3 g/cm3
3
(C) 3,33 g/cm
11. Sebuah benda bila dicelupkan dalam air
1
maka bagian akan muncul di permukaan.
3
Bila benda dicelupkan ke dalam suatu
8
larutan dengan rapat jenis
g/cm3 maka
9
baigan yang muncul di permukaan adalah
....
(A) 14 bagian
(D) 23 bagian
(B) 13 bagian
(E) 34 bagian
(C) 12 bagian
12. Gabus berbentuk kubus dengan massa m
dan massa jenis d
(sisi-sisinya = h)
diikatkan dengan tali yang lembut dan
ringan, lalu dicelupkan ke dalam air seperti
pada gambar. Rapat massa air = p. Gaya
yang dialami oleh pegas sama dengan ...
pegas
gabus
air
(A) –h3 (p – mlh3) g
(B) h3 (p+d) g
(C) (m+h3p) g
(D) h3 (p – d) g
mg
(E)
d
13. Massa sesungguhnya dari sebuah benda
adalah 300 g. Jika ditimbang di dalam air
massanya seolah-olah menjadi 225 g, dan
jika ditimbang di dalam suatu cairan lain
massanya seolah-olah menjadi 112,5 g. Jika
diandaikan rapat jenis air adalah 1 g/cm3,
maka rapat jenis cairan itu ....
(A) 0,83 g/cm3
8
(B) 1,20 g/cm2
(C) 2,50 g/cm3
(D) 2,67 g/m3
(E) tak ada jawaban yang benar
14. Sebuah logam C merupakan campuran dari
logam A dan logam B, massanya 200 gram
jika ditimbang di udara, sedangkan jika
ditimbang di dalam air, massa yang tampak
185 gram. Jika kerapatan logam A 20
gram/cm3. kerapatan logam B 10 gram/cm3
dan kerapatan air 1 gram/cm3, maka massa
logam A sebesar ....
(A) 15 g
(D) 100 g
(B) 30 g
(E) 133,33 g
(C) 66,67 g
15. Sebuah balok kayu dengan massa jenis 800
kg/m3 terapung di air. Selembar aluminium
dengan massa 54 g dan massa jenis 2700
kg/m3 diikatkan di atas kayu sehingga
sistem ini melayang dalam air. Volume
balok kayu itu adalah ....
(A) 680 cm3
(D) 200 cm3
(B) 340 cm3
(E) 180 cm 3
3
(C) 270 cm
19. Sebuah pipa kapiler yang mempunyai
kapilaritas h di dalam zat cair A, jika
dicelupkan dalam larutan B kapilaritasnya
menjadi b. Apabila massa jenis A dua kali
massa jenis B, perbandingan h dan b adalah
....
(A) 1 : 2
(D) 4: 1
(B) 2 : 1
(E) 1 : 1
(C) 1 : 4
20. Sebuah pipa kapiler berdiamater 23 mm
dimasukkan tegak lurus ke dalam bejana
yang berisi raksa (massa jenis = 13,62
g/cm3). Sudut kontak antara raksa dengan
pipa ialah 143o (sin 37 = 0,6). Bila tegangan
permukaan zat cair adalah 0,48 N/m, maka
turunnya raksa dalam pipa kapiler dihitung
dari permukaan zat cair dalam bejana (g=10
m/s2) adalah ....
(A) 1,20 cm
(D) 2,27 cm
(B) 1,69 cm
(E) 3,00 cm
(C) 2,00 cm
=====O0O=====
16. Serangga dapat berjalan pada permukaan
air karena ....
(A)berat jenis serangga lebih kecil daripada
air
(B) berat jenis serangga lebih besr daripada
air
(C) berat jenis serangga sama dengan air
(D)adanya gaya apung Archimedes
(E) adanya tegangan permukaan air
17. Zat cair dalam bejana mempunyai
permukaan berbentuk cekung jika ....
(A)sudut sentuh tumpul
(B) gaya adhesi lebih kecil daripada gaya
kohesi
(C) gaya adhesi lebih besar daripada gaya
kohesi dan sudut sentuhnya sama
dengan 90o
(D)gaya adhesi lebih besar daripada gaya
kohesi dan sudut sentuhnya lebih dari
90o
(E) gaya adhesi lebih besar daripada gaya
kohesi dan sudut sentuhnya kurang dari
90o
18. Sebuah pipa kapiler yang berjari-jari R
mempunyai kapilaritas 5 milimter. Apabila
jari-jari pipa diubah menjadi 0,5 R,
kapilaritas pipa menjadi ....
(A) 2,5 mm
(D) 10 mm
(B) 5 mm
(E) 12,5 mm
(C) 7,5 mm
9
persatuan waktu melalui suatu pipa dengan luas
penampang A dan dengan kecepatan v.
B. FLUIDA DINAMIS
1. Aliran Fluida
Aliran fluida pada dasarnya dibedakan dalam 2
macam, yaitu :
1. Aliran laminar / stasioner / streamline.
2. Aliran turbulen
a). Aliran laminar / stationer / streamline
Suatu aliran dikatakan laminar / stasioner /
streamline apabila setiap partikel yang melalui
titik tertentu selalu mempunyai lintasan (garis
arus) yang tertentu pula.
Partikel-partikel yang pada suatu saat tiba
di K akan mengikuti lintasan yang terlukis pada
gambar di bawah ini. Demikian partikelpartikel yang suatu saat tiba di L dan M.
K
L
M
=
V
 A.v
t
 = debit fluida dalam satuan SI
Vol = volume fluida
A = luas penampang tabung alir
v = kecepatan alir fluida
(m3/det)
(m3)
(m2)
(m/det)
3. Persamaan Kontinuitas
Perhatikan tabung alir di bawah ini. A1
adalah penampang lintang tabung alir yang
besar dan A2 adalah penampang tabung kecil.
V1 kecepatan alir fluida pada ketinggian h1, dan
V2 kecepatan alir fluida pada ketinggian h2.
N
Kecepatan setiap partikel yang melalui titik
tertentu selalu sama. Misalkan setiap partikel
yang melalui K selalu mempunyai kecepatan
vK.
b). Aliran turbulen
Aliran turbulen ditandai oleh adanya aliran
berputar. Ada partikel-partikel yang memiliki
arah gerak berbeda dan bahkan, berlawanan
dengan arah gerak keseluruhan fluida.
  
 
 
Pembahasan dalam bab ini dibatasi pada
fluida ideal yang memiliki ciri-ciri :
a) Inkompresibel : Yaitu massa jenis
fluida tidak tergantung pada tekanan.
b) Laminer : Yaitu aliran yang beraturan
tidak berputar-putar.
c) Stationer (tunak) Yaitu kecepatan aliran
fluida pada setiap titik sembarang selalu
tetap (konstan)
d) Non-viskos (fluida tidak kental) Yaitu
keadaan fluida yang mengabaikan
gesekan yang muncul.
2. Debit
Fluida mengalir dengan kecepatan tertentu,
misalnya v meter per detik. Penampang tabung
alir seperti terlihat pada gambar di atas
berpenampang A, maka yang dimaksud dengan
debit fluida adalah volume fluida yang mengalir
A2, P2
v2
h2
A1, P1
h1
v1
Bidang acuan
Banyaknya fluida yang masuk ke tabung alir
dalam waktu t detik adalah :
.A1.v1. t dan dalam waktu yang sama
sejumlah fluida meninggalkan tabung alir
sebanyak .A2.V2. t. Jumlah ini tentulah sama
dengan jumlah fluida yang masuk ke tabung alir
sehingga :
.A1.v1. t = .A2.v2. t
Jadi :
A1v1 = A2.v2
Persamaan ini disebut : Persamaan kontinuitas
A.v yang merupakan debit fluida sepanjang
tabung alir selalu konstan (tetap sama nilainya),
walaupun A dan v masing-masing berbeda dai
tempat yang satu ke tempat yang lain. Maka
disimpulkan :
 = A1.v1 = A2.v2 = konstan
10
4. Hukum Bernoulli.
Keterangan :
Hukum Bernoulli merupakan persamaan
pokok hidrodinamika untuk fluida yang
mengalir dengan arus streamline. Di sini
berlaku hubungan antara tekanan, kecepatan
alir dan tinggi tempat dalam satu garis lurus.
Hubungan tersebut dapat dijelaskan sebagai
berikut :
Perhatikan gambar tabung alir seperti pada
gambar diatas. Jika tekanan P1 pada penampang
A1, maka gaya yang dilakukan terhadap
penampang besar adalah P1.A1, sedangkan pada
penampang kecil mendapat gaya dari fluida
sebesar P2.A2. Dalam waktu t detik dapat
dianggap bahwa fluida pada penampang besar
tergeser sejauh v1. t dan untuk penampang
kecil tergeser sejauh v2. t ke kanan. Jadi usaha
yang dilakukan terhadap penampang besar
adalah : P1.A1.v1. t sedangkan usaha yang
dilakukan pada penampang kecil sebesar : P2.A2.v2. t Jadi usaha total yang dilakukan
gaya-gaya tersebut besarnya :
P1 dan P2 = tekanan yang dialami oleh fluida
v1 dan v2 = kecepatan alir fluida
h1 dan h2 = tinggi tempat dalam satu garis lurus
 = Massa jenis fluida
g = percepatan grafitasi
5. Aplikasi Persamaan Bernoulli
a) Gaya Angkat Sayap Pesawat Terbang
Pesawat terbang memiliki bentuk sayap
mirip sayap burung, yaitu melengkung dan
lebih tebal di bagian depan dibanding bagian
belakangnya. Bentuk sayap seperti ini
dinamakan aerofoil.
Bentuk ini menyebabkan aliran udara di
bagian atas lebih besar daripada di bagian
bawah (v2 > v1).
Wtot = (P1.A1.V1 - P2.A2.V2) t
Dalam waktu t detik fluida dalam tabung alir
besar bergeser ke tabung alir kecil dan
mendapat tambahan energi sebesar :
Emek = Ek + Ep
Emek = ( ½ m . v22 – ½ m.v12) + (mgh2 – mgh1)
= ½ m (v22 – v12) + mg (h2 – h1)
Keterangan :
 h2-h1 = beda tinggi penampang besar
dan kecil
 m
= massa fluida dapat dinyatakan
sebagai :
m = .A1.v1. t = .A2.v2. t
Menurut Hukum kekekalan Energi haruslah :
Wtot = Emek
Dari persamaan-persaman di atas dapat
dirumuskan persaman :
m
m
P1
+ ½ m.v12 + mgh1 = P2
+ ½ m.v22 +

mgh2
Suku-suku persamaan
dimensi usaha.

ini
memperlihatkan
Dengan membagi kedua ruas dengan
m

maka di dapat persamaan :
P1 + ½ .v12 +  g h1 = P2 + ½ .v22 +  g h2
Suku-suku persamaan di atas memperlihatkan
dimensi tekanan.
Dari persamaan Bernoulli kita dapatkan :
P1 + ½ .v12 +  g h1 = P2 + ½ .v22 +  g h2
Ketinggian kedua sayap dapat dianggap sama
(h1 = h2), sehingga  g h1 =  g h2.
Dan persamaan di atas dapat ditulis :
P1 + ½ .v12 = P2 + ½ .v22
P1 – P2 = ½ (v22 – v12)
Jika v2 > v1 maka dapatkan P1 > P2.
Untuk luas penampang sayap A, akan
bekerja gaya dari bawah F1 = P1 . A dan gaya
dari atas F2 = P2 . A. Jika didapatkan F1 > F2,
maka beda gaya pada bagian bawah dan bagian
atas (F1 – F2) menghasilkan gaya angkat pada
pesawat terbang. Jadi, gaya angkat pesawat
terbang dirumuskan sebagai :
F1 – F2 = ½  A(v22 – v12)
Dengan  = massa jenis udara (kg/m3)
11
b) Venturimeter
Venturimeter adalah alat yang dipasang di
dalam suatu pipa aliran untuk mengukur
kelajuan cairan.
h
A1
P1
v1
A2
P2
v2
Dari persamaan Bernoulli untuk pipa
horizontal yang memiliki ketinggian yang sama
berlaku : P + ½ .v2 = konstan
Dari persamaan hukum bernoulli :
2
2
P1 + ½ .v1 +  g h1 = P2 + ½ .v2 +  g h2
Jika cairan yang akan diukur kelajuannya
mengalir pada titik-titik yang tidak memilki
perbedaan ketinggian (h1 = h2), maka :
2
2
P1 – P2 = ½ (v2 – v1 )
(*)
Dari persamaan kontinuitas A1v1 = A2.v2,
A
maka : v 2  1 v1
(**)
A2
jika persamaan (**) dimasukkan pada
persamaan (*), maka di dapat
 A  2 
P1 – P2 = ½  v1  1   1
 A2 

Dari gambar venturimeter tampak bahwa :
P1 – P2 = gh, sehingga
2


2  A1 
gh = ½  v1    1
 A2 

PT + ½ .vT2 = PS + ½ .vS2
Bila kelajuan gas aliran dibuat tegak lurus
sehingga kelajuan gas berkurang sampai ke nol
di S (vS = 0), maka :
PT + ½ .vT2 = PS → PS - PT = ½ .vT2 (*)
Di lain sisi selisih tekanan dalam
manometer menyebabkan ketinggian zat cair
berbeda sebesar h. Bila massa jenis zat cair  ' ,
maka didapat PS - PT =  ' gh
(**)
Dengan menyamakan (*) dan (**)
½ .vT2 =  ' gh
diperoleh laju aliran gas dalam tabung pitot
2
v1 
2
 A1 
   1
 A2 
2 gh
A
1   2
 A1



2  ' gh

 ' = massa jenis zat cair (kg/m3)
 = massa jenis udara (kg/m3)
d) Penyemprot Parfum
2 gh
Dengan cara yang sama untuk kecepatan alir v2
v2 
vT 
Saat bola karet pada penyemprot parfum
ditekan, udara akan bergerak cepat yang
mengakibatkan tekanan udara pada bagian atas
tabung berkurang. Perbedaan tekanan antara
bagian atas dan bawah tabung mengakibatkan
terjadinya aliran udara keatas pada tabung.
2
c) Tabung Pitot
Tabung pitot digunakan untuk mengukur
kelajuan gas. Tabung ini terdiri dari dua bagian
yaitu tabung luar (tabung statis) dan tabung
dalam (tabung pitot)
Selanjutnya cairan akan ikut keluar dari
tabung berbentuk semburan halus.
12
e) Bak Penampung Air Bocor
Pada kasus bak penampung air yang bocor
dapat diterapkan dua materi yang saling terkait
yaitu hukum bernoulli dan gerak peluru. Saat
air mulai turun dari dalam bak dan keluar dari
bak berlaku hukum bernoulli dan saat air
'memancar' dari bak membentuk lintasan gerak
peluru.
v1
v2
 Contoh Soal dan Pembahasan :
1. Debit aliran adalah jumlah fluida yang
mengalir melalui suatu penampang pipa tiap
....
(F) satuan volume
(G) satuan luas
(H) satuan panjang
(I) satuan waktu
(J) satuan massa
Jawaban : D
Ingat debit  =
h1
h2
V
 A.v
t
2. Perhatikan gambar di bawah ini
x
Jarak lintasan air maksimum adalah : x = v2 . t
Dari hukum Bernoulli :
P1 + ½ .v12 +  g h1 = P2 + ½ .v22 +  g h2
Jika tekanan udara luar diatas bak sama
dengan tekanan udara luar di lubang kebocoran
P1 = P2 dan dianggap kecepatan air yang keluar
v2 jauh lebih besar dari turunnya air v1 (v1<<<
v2), maka v1 dapat diabaikan terhadap v2,
sehingga persamaan diatas menjadi :
 g h1 = ½ .v22 +  g h2
v2  2 g (h1  h2 )
Dari persamaan gerak peluru :
2h2
, sehingga
t
g
x=
2 g (h1  h2 )
2h2
g
x  2 h2 h1  h2 
=====O0O=====
Air mengalir pada pipa dari A ke B. apabila
luas penampang A dan B masing-masing a
meter persegi dan b meter persegi dan
kecepatan air di A dan B masing-masing p
meter per sekon dan q meter per sekon,
diperoleh hubungan ....
(A)a : b = p: q
(D) ab = pq
(B) ab = pq
(E) a : b = q : p
(C) aq : bp
Jawaban : E
A1v1 = A2.v2 → a p = b q atau dapat ditulis
a:b=q:p
3. Sebuah pipa silindris yang lurus mempunyai
dua macam penampang masing-masing
dengan luas 200 m2 dan 100 m2. Pipa
tersebut diletakkan secara horizontal,
sedangkan air di dalamnya mengalir dari
arah penampang besar ke penampang kecil.
Apabila kecepatan arus di penampang besar
adalah 2 m/s, maka kecepatan arus di
penampang kecil adalah ....
(A) 1/4 m/s
(D) 2 m/s
(B) 1/2 ms
(E) 4 m/s
(C) 1 m/s
Jawaban : E
A1v1 = A2.v2 → v2 =
v2 
A1
v1
A2
200
2 m / s  4 m / s
100
4. Air mengalir dalam suatu pipa yang luas
penampangnya 10 cm2 untuk mengisi penuh
bak yang volumenya 1 m3 dalam waktu 5
menit. Berapakah kecepatan aliran tersebut?
13
(A) 6,66 m/s
(B) 3,33 m/s
(C) 1/300 m/s
(D) 0,33 m/s
(E) 0,1 m/s
Jawaban : B
V
V
=
 A.v → v 
t
A t
1
v  3
m / s  v  3,33 m / s
10 300 
5. Air mengalir ke dalam sebuah bak dengan
debit konstan 0,5 liter/sekon. Jika bak
tersebut berukuran 1 x 1 x m3, maka bak
tersebut akan penuh dalam waktu ....
(A) 33,3 menit
(D) 33,3 sekon
(B) 3,33 menit
(E) 3,33 sekon
(C) 333 menit
Jawaban : A
103 3
Diketahui  = 0,5 lt/dt =
m / dt
2
V
V
=
 A.v  t 
t

V
1
t   t   3 dt  2000 dt
10

2
t  33,3 menit
6.
Tinggi permukaan air pada tangki adalah
1,25 m, sedang tempat kebocoran 80 cm
dari dasar tangki. Maka jauh tempat
jatuhnya air (x) = ....
(A) 0,8 m
(D) 1,25 m
(B) 1,0 m
(E) 1,5m
(C) 1,2 m
Jawaban : C
Perhatikan gambar berikut :
v1
h1
v2
x  2 8045 cm  120 cm
7. Air mengalir dari A ke B dalam pipa yang
berbentuk seperti pada gambar di bawah ini,
Tinggi permukaan air pada masing-masing
pipa adalah ....
A) a = b = c
(D) a > b < c
(B) a > b > c
(E) a < b > c
(C) a < b < c
Jawaban : B
Hal tersebut berdasar Asas Bernoulli yang
menyatakan :”Pada pipa mendatar tekanan
fluida paling besar adalah pada bagian yang
kelajuan alirnya paling kecil, dan tekanan
paling kecil adalah pada bagian yang
kelajuan alirnya paling besar”
8. Air terjun setinggi 10 m dengan debit 50
m3/s dimanfaatkan untuk memutar turbin
yang menggerakkan generator listrik. Jika
25% energi air dapat berubah menjadi
energi listrik dan g = 10 m/s2, maka daya
keluaran generator adalah …
(A) 0,9 MW
(D) 1,30 MW
(B) 1,10 MW
(E) 1,50 MW
(C) 1,25 MW
Jawaban : C
E
  output  Pout . t   m g h
Einput
Pout . 
mgh
t
mengingat  
 Pout . 
 V gh
t
dengan
m
V
 m   V dan  
V
t
Pout .     g h
25

Pout . 
103 50 10 10  W  1,25 MW
100
9. Perhatikan gambar berikut
h2
x
Menurut teori untuk bak bocor :
x  2 h2 h1  h2  , maka diperoleh :
Kecepatan aliran gas dapat ditentukan
dengan alat seperti pada gambar. Apabila
perbedaan tinggi raksa antara kedua kaki
14
setinggi h dan massa jenis gas dan raksa
berturut-turut 1 dan 2, maka kecepatan
aliran gas sebesar ....
2  2 .g .h
(A) v 
 Soal-soal :
1.
1
(B) v 
(C) v 
2 1 .g.h
2
Hukum utama hidrostatika dapat diturunkan
dari persamaan Bernoulli. Apabila A
tekanan hidrostatika di A dan B tekanan
hidrostatika di B serta  massa jenis cairan,
maka diperoleh hubungan ....
(A) A = gh1 dan B = gh2
(B) A = gh2 dan B = gh1
(C) A = B = gh1
(D) A = B = gh2
(E) A = B (h2-h1).g
2 1 . 2
g .h
(D) v  2 1 . 2 g.h
(E) v 
2  2 .g
1.h
Jawaban : A
Lihat tentang konsep tabung pitot
10. Perhatikan pernyataan berikut
1. Rumus fluida yang mengalir adalah
1
P+gh + v2= konstan
2
2. Rumus fluida yang diam adalah P1 = P2
+ g (h2-h1)
3. Hukum Bernouli sama dengan hukum
termodinamika
Pernyataan di atas yang berkaitan dengan
hukum Bernoulli adalah ....
(A) 1, 2, dan 3
(D) 2
(B) 1 dan 3
(E) 3
(C) 1 dan 2
Jawaban : C
Lihat kembali teori dasar fluida sebelumnya
=====O0O=====
2.
1
2
Gambar di atas adalah sebuah tangki yang
sangat besar. Titik 2 tepat terletak pada
sebuah lubang pada tangki. Kecepatan air
yang mengalir melalui titik 1 diabaikan.
Titik 1 dan 2 terletak sejajar, sedangkan
perbedaan tekanannya 2 x 105 N/m2, maka
kecepatan air di titik 2 adalah ....
(air = 1 g/cm3)
(A) 5 m/s
(D) 20 m/s
(B) 10 m/s
(E) 25 m/s
(C) 12 m/s
3. Hal – hal di bawah ini bekerja berdasarkan
hukum Bernoulli, kecuali ....
(A) gaya angkat pada sayap pesawat
terbang
(B) tabung pitot
(C) tabung venturimerter
(D) hukum utama hidrostatika
(E) kempa hidrolik
4. Perhatikan gambar di bawah ini
Dua bejana, 1 dan 2 , masing-masing berisi
cairan yang massa jenisnya  dan 2 . Pada
bagian bawah masing-masing bejana diberi
saluran yang luas penampangnya sama.
Apabila tinggi permukaan cairan sama,
maka perbandingan kecepatan aliran cairan
di bejana 1 dan 2 yaitu ....
15
(A)1 : 1
(B) 1 : 2
(C) 1 : 4
(D) 4 : 1
(E) 2 : 1
5. Sebuah tangki dengan tinggi 2 m diletakkan
di atas penyangga setinggi 8 m. Pada
permukaan samping bawah tangki terdapat
lubang kecil. Kemudian tangki diisi penuh
dengan air, dan air mengalir keluar melalui
lubang kecil tersebut. Jarak mendatar
terjauh yang dapat dicapai oleh aliran air
yang keluar dari tangki adalah ....
(A) 4 m
(D) 10 m
(B) 6 m
(E) 12 m
(C) 2 m
6. Bak air dengan luas penampang 1 m2 dan
tinggi 1 m diisi air dari keran yang luas
penampangnya 2 cm2, kecepatan alirnya 5
m/s. Air akan tumpah setelah ... menit.
(A) 10
(D) 18,6
(B) 15 ½
(E) 21,7
(C) 16,7
7. Suatu bejana diisi dengan zat cair sampai
setinggi H. Pada tinggi bejana terdapat
lubang
yang letaknya h di bawah
permukaan zat cair. Zat cair akan jatuh ke
permukaan sejauh ....
(A) 120 liter
(B) 40 liter
(C) 60 liter
10. Sebuah bak diisi air setinggi 20 m. Di sisi
bak dibuat 2 lubang yang masing-masing
berjarak 2 m dari permukaan dan dasar
tabung. Perbandingan jauh jarak air yang
dipancarkan dari lubang-lubang tersebut....
(A) 1 : 2
(D) 1 : 3
(B) 1 : 1
(E) 3 : 1
(C) 2 : 1
11. Suatu lubang terdapat pada sebuah bak air.
Jarak antara lubang ke permukaan air = h1
dan jarak lubang ke alas bak air = h2. Agar
air jatuh ke lantai dengan jarak horizontal
yang maksimum, maka h1 : h2 = ....
(A) 1 : 2
(D) 1 : 2
(B) 2 : 1
(E) 1 : 1
(C) 2 : 1
12. Sebuah tangki berisi air diletakkan di tanah
(lihat gambar). Tinggi permukaan air 1,25
m dari tanah. Pada ketinggian 0,8 m dari
tanah terdapat lubang kebocoran, sehingga
air mengalir melalui lubang tersebut dengan
kecepatan .... (g = 10 m/s2)
1,25 m
(A) R= 2 H ( H  h ) dari dinding bejana
(B)
R= 2 gh
(C)
R=2 h ( H  h ) dari dinding bejana
dari dinding bejana
(D) 80 liter
(E) 100 liter
(A) 0,45 m/s
(B) 3 m/s
(C) 8 m/s
80 cm
(D) 9 m/s
(E) 12,5 m/s
13. Perhatikan gambar berikut
(D) R= 2 gh dari dinding bejana
(E) R= h( H  h) dari dinding bejana
8. Pada bak yang berisi air setinggi 1 meter
(diukur dari alasnya) terdapat kebocoran
kecil pada dindingnya, yang jauhnya 20 cm
dari permukaan air. Di manakah harus
dibuat sebuah lubang lagi (diukur dari
alasnya) sehingga tempat jatuhnya berimpit
dengan kebocoran yang pertama?
(A) 80 cm
(D) 20 cm
(B) 60 cm
(E) 10 cm
(C) 40 cm
9. Sebuah tangki air terbuka memiliki
kedalaman 0,8 m. Sebuah lubang dengan
luas penampangnya 5 cm2 dibuat di dasar
tangki. Berapa massa air per menit yang
mula-mula akan keluar dari lubang itu?
Tekanan di pipa 1 dan 2 berturut-turut 1
dan 2. Sedangkan v1 dan v2 merupakan
kecepatan aliran air di pipa 1 dan 2 sebesar
h dan massa jenis air sebesar , diperoleh
hubungan ....
(A) v1 - v2 = gh
(D) 2-1 = gh
(B) 1-2= gh
(E) 1-2 = gh
(C) v1 - v2 = gh
14. Perhatikan gambar berikut
16
Pernyataan di bawah ini menyatakan aliran
air dari A ke C melalui B, kecuali ....
(A) Kecepatan aliran air di A < di B
(B) Tekanan oleh air di A < di B
(C) Kecepatan aliran air di B > di C
(D) Debit air di A = di B
(E) Tekanan oleh air di A>C
15. Sebuah pipa silindris yang lurus mempunyai
dua macam penampang. Pipa tersebut
diletakkan secara horizontal, sedangkan air
di dalamnya mengalir dari arah penampang
besar yang diameternya 10 cm dengan
tekanan 1,4 x 105 N/m2 dan laju 1 m/s.
Supaya tekanan dalam penampang kecil
sama dengan tekanan udara (1 x 105 N/m3),
maka diameter penampang kecil adalah ....
(A) 1 cm
(D) 6 cm
(B) 2 cm
(E) 9 cm
(C) 4 cm
16.
A
6m
maka jauh tempat jatuhnya air diukur dari
dinding akuarium adalah ....
(A) 0,5 m
(D) 4 m
(B) 1 m
(E) 1,5 m
(C) 2 m
19.
h
x
Sebuah tangki air pada bagian bawahnya
terdapat lubang hingga air memancar keluar
membentuk sudut 60o seperti terlihat pada
gambar. Jika jarak pancarnya x = 803 cm,
maka untuk g = 10 m/s2, tinggi air (h) dalam
tangki adalah ....
(A) 20 cm
(D) 128 cm
(B) 80 cm
(E) 160 cm
(C) 83 cm
20. Pipa pindah pada gambar disamping
tampaknya bekerja melawan gaya gravitasi.
Berdasarkan asas Bernoulli, kelajuan fluida
v adalah ....
1m
Pada gambar di atas, tinggi permukaan air
pada bak A adalah 6 m dari lantai. Air
dialirkan ke bak B melalui pipa. Tinggi
ujung pipa dari lantai = 1 meter. Penampang
pipa = 0,5 cm2. Debit air yang keluar lewat
pipa adalah ....
(A) 100 cm3/s
(D) 500 cm3/s
3
(B) 200 cm /s
(E) 1000 cm3/s
(C) 300 cm3/s
y
h
v
(A)
2 gh
(D)
g (h  y )
(B)
2 gy
(E)
2 g (h  y )
(C)
2 g (h  y )
=====O0O=====
17.
h
x
Sebuah akuarium diisi air mellaui sebuah
keran yang debitnya 0,5 liter per sekon.
Ternyata ada lubang yang luasnya 1,25 cm2
tepat di dasar akuarium. Maka, tinggi air
maksimum (t) yang dapat diisi adalah ....
(A) 20 cm
(D) 80 cm
(B) 40 cm
(E) 100 cm
(C) 60 cm
18. Jika pada soal nomor 26 tinggi dasar
akuarium dari lantai (h) adalah 1,25 m,
17
Tambahan
1. Besarnya gaya gesekan yang bekerja pada
benda yang jatuh di dalam zat cair
bergantung pada besara berikut, kecuali ....
(A) kecepatan benda
(B) viskositas zat cair
(C) ukuran benda
(D) massa jenis zat cair
(E) tegangan permukaan zat cair
2. Sebuah logam bergerak vertikal ke bawah
dengan kelajuan tetap 0,5 cm/s di dalam
suatu fuida yang mempunyai massa jenis 2
g/cm2. jari-jari bola 0,9 cm dan massa
jenisnya 7 g/cm3. Jika percepatan gravitasi
bumi 10 m/s2, maka koefisien viskositas
fluida tersebut adalah ....
(A) 1,8 N s/m2
(D) 72 N s/m2
2
(B) 18 N s/m
(E) 180 N s/m2
(C) 36 N s/m2
3.
•A
B•
C•
D•
Sumbu fluida terdapat dalam bejana seperti
gambar diatas. Pernyataan yang benar
adalah ....
(A)Tekanan di A = tekanan di B
(B) Tekanan di B > tekanan di C
(C) Tekanan di C < tekanan di D
(D)Tekanan di C< tekanan di B
(E) Tekanan di B, C dan D sama
4. Faktor yang menentukan tekanan zat cair
adalah ....
(A) massa jenis zat cair
(B) massa jenis dan volume zat cair
(C) massa jenis dan kedalaman zat cair
(D) volume dan kedalaman zat cair
(E) massa jenis, volume, dan kedalaman zat
cair
5. Sebuah pipa kapiler dalam zat cair A
mempunyai sudut sentuh . Apabila zat cair
B mempunyai sudut sentuh , pernyataan di
bawah ini yang benar adalah ....
(A)kapilaritas pada zat cair A dan B sama
jika  > 
(B) kapilaritas pada zat cair A > kapilaritas
pada zat cair B jika  > 
(C) kapilaritas pada zat cair B > kapilaritas
pada zat cair A jika  > 
(D) kapilaritas pada zat cair A > kapilaritas
pada zat cair B jika  = 
(E)
kapilaritas pada zat cair B >
kapilaritas pada zat cair A jika  = 
6. Kapal terapung di atas air karena ....
(A)berat kapal lebih kecil dari gaya
Archimedes
(B) berat kapal lebih besar dari gaya
Archimedes
(C) berat kapal sama dengan gaya
Archimedes
(D) berat jenis kapal lebih besar dari massa
jenis air
(E) massa jenis kapal sama dengan massa
jenis air
7. Tekanan yang dilakukan pada zat cair akan
diteruskan ke semua arah sama besar,
merupakan pernyataan ....
(A) hukum utama hidrostatis
(B) hukum Archimedes
(C) hukum Pascal
(D) hukum Boyle
(E) hukum kekelan energi mekanik
8. Permukaan raksa pada pipa kapiler adalah
...
(A)sama tinggi dengan permukaan raksa
pada bejana
(B) lebih tinggi daripada permukaan raksa
pada bejana
(C) lebih rendah daripada permukaan raksa
pada bejana
(D)tergantung bejananya
(E) tergantung bahan pipa yang digunakan
9. Sebuah pipa kapiler dimasukkan ke dalam
bejana berisi zat cair. Kenaikan permukan
zat cair dalam pipa kapiler tidak bergantung
pada ....
(A)sudut kontak
(B) tegangan permukaan
(C) massa jenis zat cair
(D)diameter pipa kapiler
(E) tekanan udara luar
10. Sebuah benda dapat melayang di dalam
suatu zat cair jika ....
(A)berat zat cair yang dipindahkan sama
dengan gaya Archimedes
(B) berat benda sama dengan gaya ke atas
(C) volume zat cair yang dipindahkan sama
dengan volume benda
(D)massa jenis benda kurang dari massa
jenis zat cair
(E) besar gaya Archimedes sama dengan
gaya ke atas
18
Soal Latihan.
1. Hitung rapat massa dan rapat massa relatif
dari gasolin bila 51 gram = 75 cm3
2. Berapa Volume dari 300 gram air raksa jika
rapat massa air raksa 13,6 g/cm3
3. Dua macam cairan A dan B dimasukkan
dalam satu bejana dan menghasilkan rapat
massa yang baru 1,4 g/cm3. Sedangkan
rapat massa cairan A = 0,8 g/cm3. Rapat
massa cairan B = 1,8 g/cm3. Hitunglah
volume masing-masing cairan dalam 1000
cm3 volume campuran.
4. Sebongkah emas dan jam tangan = 100
gram. Rapat massa emas = 19,3 g/cm3 dan
rapat massa jam tangan = 2,6 g/cm3,
sedangkan rapat massa bongkah emas + jam
tangan = 6,4 g/cm3. Hitunglah massa emas
dalam jam tangan tersebut.
5. Berapa galon minyak biji kapas seberat 400
dyne dengan rapat massa relatif 0,926
g/cm3. (1 galon air = 8,34 dyne).
6. 1 liter susu = 1032 gram. 4 % dari volume
tersebut berupa lemak keju yang rapat
massanya 0,865 g/cm3. Berapa rapat massa
dari susu yang telah diambil lemaknya
tersebut.
7. Hitung tekanan pada 76 cm di bawah
permukaan :
a. Air dalam sistem MKS dan
CGS.
b. Air raksa dalam sistem MKS dan
CGS.
8. Apabila sebuah kapal selam menyelam
sedalam 60 m, berapa besar tekanan yang
dialami kapal selam tersebut. (Rapat massa
air laut = 1,03 g/cm3).
9. Seorang pemain sepak bola yang beratnya
75 kgf memakai sepatu yang masing-masing
dilengkapi dengan 6 buah paku (Spike).
Penampang tiap paku 0,6 cm2. Hitung
tekanan di bawah salah satu paku pada
tanah.
10. Sebuah pipa besi dipakai untuk menopang
sebuah lantai yang melentur yang beratnya
1500 kgf. Garis tengah dalam pipa itu 10
cm, garis tengah luarnya 12 cm. Hitung
tekanan yang dilakukan oleh ujung bawah
pipa itu pada tanah.
11. Sebuah bejana berbentuk kerucut, luas dasar
1 dm2 penuh berisi air. Berapa besar gaya
yang bekerja pada dasar kerucut jika
volumenya 1 dm3 ?
12. Balok besi berukuran 20 cm x 10 cm x 5,5
cm terletak pada dasar bejana dengan bagian
yang berukuran 10 cm x 5,5 cm sebagai
dasar balok besi. Jika tinggi air dalam
bejana 1,4 m, hitunglah gaya yang bekerja
pada dinding balok yang berbeda. (Gaya
Hidrostatis).
13. Sebuah bejana yang berukuran panjang 40
cm, lebar 30 cm dan tinggi 25 cm berisi
minyak sebanyak 19,2 kgf.
Rapat massa minyak = 0,8 g/cm3 ; g = 10
m/det2 ; BAR = 76 cmHg.
a. Tentukan tekanan total dan gaya total
yang dialami dasar bejana.
b. Tentukan tekanan hidrostatis dan gaya
hidrostatis yang dialami oleh dinding
bejana.
14. Sebuah corong, lubang atas berdiameter 11
cm dan lubang bawah berpenampang
dengan diameter 1,6 cm. Tinggi corong 2
dm, penuh berisi air. Berapa gaya total yang
menekan pada ibu jari yang menutup lubang
dimana BAR = 75 cmHg.
15. Balok berukuran panjang 21 m, lebar 14 m
dan tebal 3,25 m terletak dalam air. Dinding
berukuran 21 m x 14 m menjadi dasar balok
dan dinding bagian atas terletak 5 m di
bawah permukaan air. Berapa besar gaya
pada dinding samping yang luas ?
16. Bejana penampung air hujan berbentuk
kubus dengan rusuk 1 m. Bejana diberi
tutup dan dipasang silinder vertikal
penampangnya 120 cm2 dan tingginya di
atas tutup adalah 3,5 m. Hitunglah gaya
hidrostatis yang dialami oleh dindingdinding bejana serta pada tutup jika silinder
penuh berisi air.
17. Sebuah silinder berisi minyak tanah (m =
0,8 g/cm3) dilengkapi dengan sebuah
penghisap dengan luas penampangnya =
154 cm2, tinggi minyak 50 cm. Di atas
penghisap terdapat beban 5 kgf. BAR = 1
atm. Tentukan gaya total yang bekerja pada
dasar dan sisi bejana. (g = 10 m/det2).
18. Luas penampang penghisap yang kecil dan
yang besar dari suatu pompa hidrolik adalah
a cm2 dan b cm2. Jika pada penghisap yang
kecil bekerja gaya A N, berapakah besar
gaya timbul pada penghisap yang besar ?
19. Pompa hidrolik mempunyai penghisap
dengan luas penampang 15 cm2 dan 3 dm2.
Jika pada penghisap yang kecil diberi beban
400 N. Berapa besar gaya pada penghisap
yang besar agar terjadi keseimbangan ?
20. Gaya besarnya 5 N pada penghisap yang
kecil dari suatu pompa hidrolik dapat
19
mengangkat beban beratnya 600 N yang
terdapat pada penghisap yang besar. Jika
penghisap yang kecil berpenampang 400
cm2, berapakah luas penampang yang besar
?
21. Suatu kempa hidrolik dapat mengangkat 1
ton mobil, jika diameter penghisap besar 50
cm, diameter penghisap kecil 10 cm.
Tentukan gaya yang harus dikerjakan pada
penghisap kecil.
22. Sebuah kempa hidrolik mempunyai torak
yang berdiameter 20 cm dan 2 m untuk
mengangkat mobil. Pada torak kecil
dilakukan gaya sebesar 100 kgf, sehingga
torak besar naik setinggi 1 cm. Tentukan
massa mobil dan berapa m turunnya torak
kecil tersebut.
23. Suatu bejana berbentuk pipa U mula-mula
diisi dengan air raksa yang massa jenisnya
13,6 g/cm3, kemudian kaki kanan
dituangkan 14 cm air lalu di atas air ini
dituangkan minyak yang massa jenisnya 0,8
g/cm3, ternyata dalam keadaan setimbang
selisih tinggi permukaan air raksa dalam
kedua kaki 2 cm. Hitung berapa cm tinggi
lajur minyak pada kaki kanan.
24. Dalam pipa U terdapat Hg (Rapat massa
13,6 g/cm3). Pada kaki kiri dituangkan air
setinggi 20 cm kemudian minyak (Rapat
massanya 0,9 g/cm3) tingginya 8 cm. Pada
kaki kanan ditambahkan alkohol (Rapat
massa 0,8 g/cm3) sehingga permukaan
minyak dan permukaan alkohol sebidang.
Berapa beda tinggi Hg pada kedua kaki pipa
?
25. Dalam pipa U terdapat Hg (Rapat massanya
13,6 g/cm3). Pada kaki kiri dituangkan air
setinggi 30 cm. Berapa tinggi minyak pada
kaki di sebelah kanan harus ditambahkan
agar permukaan air dan permukaan minyak
sebidang ? (Rapat massa minyak 0,9 g/cm3).
26. Kaki kiri dan kanan sebuah pipa U masingmasing berdiameter 3 cm dan 11/2 cm, mulamula diisi air raksa (Hg = 13,6 g/cm3).
Kemudian kaki kiri diisi alkohol (Rapat
massa 0,8 g/cm3), kaki kanan diisi bensin
(Rapat massa 0,7 g/cm3) setinggi 2 cm,
sehingga tinggi air raksa di kaki kanan naik
1 cm. Hitunglah volume alkohol yang
dituangkan.
27. Ke dalam pipa U yang berdiameter 5 cm,

mula-mula diisi air raksa (Rapat massa 13,6
g/cm3). Kemudian kaki kiri diisi dengan
gliserin (Rapat massa 1,25 g/cm3). Tentukan
volume gliserin yang diperlukan agar air
raksa pada kaki kanan naik ½ cm.
28. Batang besi dalam air berat semunya 372 N.
Berapa berat semu besi tersebut dalam
cairan yang densitasnya 0,75 g/cm3 jika
berat besi 472 N.
29. Suatu gelas beratnya 25 N di udara, 15 N di
air, dan 7 N di dalam asam belerang, hitung
rapat massa asam belerang.
30. Sebuah benda mempunyai berat 100 N di
udara dan 60 N di minyak (Rapat massanya
0,8 g/cm3). Hitung massa jenis benda
tersebut.
31. Sepotong besi massanya 450 gram, di dalam
air massanya berkurang menjadi 390 gram.
Tentukan rapat massa besi.
32. Sebuah patung berongga mempunyai berat
210 N dan jika ditimbang di dalam air
beratnya 190 N. Patung tersebut terbuat dari
logam (Rapat massa 21 g/cm3). Tentukan
volume rongga patung tersebut. (g = 10
m/det2).
33. Sebatang emas (Rapat massa 19,3 g/cm3)
dicurigai mempunyai rongga. Beratnya di
udara 0,3825 N dan di air 0,3622 N. Berapa
besar rongga tersebut ?
34. 50 gram gabus (Rapat massa 0,25 g/cm3)
diikatkan pada timbal sehingga gabungan
benda melayang di dalam air. Berapa berat
timbal (Rapat massanya 11,3 g/cm3).
35. Sebuah kubus dari gabus dibebani dengan
sepotong logam sehingga melayang dalam
aseton. Jika massa logam 77 gram, rapat
massa gabus 0,24 g/cm3, rapat massa logam
8,8 g/cm3, rapat massa aseton 0,8 g/cm3.
Tentukan rusuk kubus.
36. Sebongkah es (Rapat massanya 0,9 g/cm3)
terapung pada air laut (Rapat massanya 1,03
g/cm3). Jika es yang timbul di permukaan
air laut 7,8 dm3. Hitunglah volume es.
37. Massa jenis es 917 kg/m3. Berapa bagian es
terletak di permukaan air.
38. Sebatang kayu yang massa jenisnya 0,6
g/cm3 terapung di dalam air. Jika bagian
kayu yang ada di atas permukaan air 0,2 m3,
tentukan volume kayu seluruhnya.
39. Sebuah kubus dari kayu (Rapat massanya
0,8 g/cm3), Mula-mula dibenamkan ke
dalam bejana kemudian dilepas sehingga
naik ke permukaan gliserin (Rapat massa
1,25 g/cm3) dan ternyata 200 cm3 dari kayu
tersebut berada di permukaan gliserin.
Tentukan :
20
a. Gaya ke atas kayu pada saat masih
berada seluruhnya dalam gliserin.
b. Gaya naik.
c. Gaya ke atas setelah benda setimbang.
d. Rusuk kubus.
40. Sebuah kawat berbentuk segitiga sama sisi
diletakkan perlahan-lahan di atas permukaan
zat cair. Tegangan permukaan zat cair 74
dyne/cm. Gaya oleh tegangan permukaan
1,776 dyne. Tentukan tinggi segitiga
tersebut.
41. Sebuah pisau silet uang berukuran 3 cm x
11/2 cm, diletakkan di atas permukaan zat
cair. Tegangan permukaan zat cair 72
dyne/cm. Tentukan berat minimum silet
tersebut agar tidak tenggelam.
42. Untuk mengangkat sebuah jarum yang
panjangnya 5 cm dari permukaan zat cair,
kecuali berat jarum itu sendiri, masih
diperlukan gaya sebesar F Newton.
Tegangan permukaan zat cair 63,1 dyne/cm.
Tentukan F.
43. Hitunglah tekanan (turunnya tinggi) pipa
kapiler berdiameter 0,4 mm dan diletakkan
vertikal yang salah satu ujungnya
dicelupkan dalam bak yang berisi air raksa.
(Rapat massa 13,6 g/cm3) dengan sudut
kontak 1500, tegangan permukaan 450
dyne/cm.
44. Sebuah pipa kapiler dimasukkan tegak lurus
ke dalam air raksa. Tegangan permukaan air
raksa 0,5 N/m. Selisih tinggi air raksa
2 cm.
didalam dan diluar pipa = ½
Diameter kapiler = 1 cm ; Rapat massa
6,8
3
Hg = 13,6 g/cm ; g = 10 m/det2. Tentukan
besarnya sudut kontak antara air raksa dan
dinding pipa.
45. Sebuah sungai lebarnya 5 meter, dengan
kedalaman yang rata diberi pintu air
sehingga terjadi perbedaan tinggi air di
kanan dan di kiri. Tinggi air di kanan 4
meter dan tinggi air di sebelah kiri 3 meter.
Jika g = 10 m/det2 dan rapat massa air
sungai 1,05 g/cm3. Tentukan perbedaan
gaya hidrostatis yang dialami oleh pintu air
tersebut.
Soal Balon Udara.
46. Sebuah balon udara volumenya 400 m3,
mengalami gaya naik 2200 N. Tentukan
gaya ke atas dan berat total balon (g = 10
m/det2).
47. Sebuah balon udara bervolume 20 m3.
Berisi H2 (Rapat massa 0,09 g/l) berat
perlengkapannya 10 kgf. Tentukan berat
beban yang dapat diangkut.
48. Sebuah balon udara mengalami gaya naik
2450 N. Berat total balon 4050 N. Tentukan
gaya ke atas dan diameter balon udara
tersebut.
LATIHAN SOAL
1. Air yang mengalir dalam sebuah pipa yang
berdiameter 6 cm berkecepatan 1,5 m/det.
Berapa kecepatan air dalam pipa yang
berpenampang dengan diameter 3 cm, jika pipa
ini dihubungkan dengan pipa pertama dan
semia pipa penuh.
( jawab : 6 m/s)
2. Pipa dengan penampang 2 cm2 dialiri air
dengan keceapatan 2 m/s. Ditanyakan :
Berapa cm3 dapat dialirkan tiap menit ( jawab :
24.000 cm3)
Berapa kecepatan alir air bila pipa dihubungkan
dengan pipa yang berpenampang 1 cm2) (jawab
: 400 cm/s)
3. Perhatikan alat sepeti tergambar di sebeelah
kanan
Berapa kecepatan air yang dipancarkan lewat
lobang
L. jika tekanan terhadap air 106 Pa dan tekanan
udara
L
Luar 105 Pa dan apabila kecepatan air dalam
reservoir
Boleh diabaikan. (jawab : 30 2 m/s)
4. Sebuah tangki berisi air dan mempunyai kran
setinggi 2 meter di atas tanah. Jika kran dibuka,
maka air akan memancar keluar dan jatuh pada
jarak horizontal sejauh 15 m dari kran. Berapa
tinggi permukaan air dari kran, jika percepatan
grafitasi bumi 10 m/s2 dan kecepatan turunnya
air boleh diabaikan. (jawab : 28,125 m)
5. Sebuah pipa panjang memiliki penampang
berbeda pada empat bagian. Luas penampang
pipa berturut-turut pada bagian 1, bagian 2,
bagian 3 adalah 150 cm2, 100 cm2 dan 50 cm2.
Laju aliran air pada bagian 1 adalah 8 m/s.
Sedangkan pada bagian 4 adalah 4,8 m/s.
Tentukanlah :
21
Debit air melalui keempat penampang itu
(jawab : 0,12 m3/s)
Luas penampang pada bagian 4 (jawab : 250
cm2)
Laju air pada bagian 2 dan 3 (jawab : 12 m/s ,
24 m/s)
6. Sebuah pipa air memiliki dua penampang
yang berbeda. Diameter masing-masing
penampang adalah 15 cm dan 10 cm. Jika laju
aliran pada penampang yang kecil adalah 9 m/s.
Berapakah laju aliran pada penampang yang
besar ? (jawab : 4 m/s)
7. Sebuah tangki berisi air, pada jarak 20 meter
di bawah permukaan air pada tangki itu terdapat
kebocoran.
Berapa kecepatan air yang memancar dari
lubang tersebut. (jawab : 20 m/s
Bila luas lubang 1 x 10-6 m2. Berapa liter
volume air yang keluar dalam 1 detik. (0,02
liter)
8. Air mengalir melalui sebuah pipa mendatar
yang luas penampangnya berbeda, penampang
X = 8 cm2, kecepatan air adalah 3 cm/s.
Tentukanlah :
Kecepatan air pada penampang Y yang luasnya
2 cm2. (jawab : 12 cm/s)
Beda tekanan antara X dan Y (jawab : 6,75
N/m2)
9. Pada suatu pipa mendatar yang luas
penampangnya 30 cm2, tekanan statis air yang
mengalir dengan aliran stasioner adalah 6,5 .
104 Pa dan tekanan totalnya adalah 6,7 . 104 Pa.
Hitung :
Kecepatan aliran air (2 m/s)
Debit air yang melalui pipa (jawab : 6 liter/s)
10. Sebuah pipa silindris lurus memiliki
diameter 10 cm. Pipa tersebut diletakkan
horizontal, sedangkan air mengalir didalamnya
dengan kecepatan 2 m/s. Diujung pipa terdapat
mulut pipa dengan diameter 1,25 cm.
Berapa kecepatan air yang keluar dari mulut
pipa. (jawab : 128 m/s).
Bila mulut pipa berhubungan dengan udara
luar, berapa tekanan air di dalam mulut pipa
jika Pbar = 1. 105 Pa. (jawab : 82,9 . 105 Pa)
Tekanan pada penampang yang besar (jawab :
5,55 . 104 Pa)
12. Dalam suatu pipa, ada air mengalir. Di
suatu tempat, laju air adalah 3 m/s, sedangkan
di tempat lian yang terletak 1 meter lebih tinggi,
laju air adalah 4 m/s.
Berapakah tekanan air di tempat yang tinggi
bila tekanan air di tempat yang rendah 2 . 104
Pa. (jawab : 6,5 .103 N/m2)
Berapa tekanan air di tempat yang tinggi bila
air dalam pipa berhenti dan tekanan air di
tempat yang rendah 1,8 .104 Pa. (jawab : 8 .103
N/m2)
13. Sebuah pipa lurus mempunyai dua macam
penampang, masing-masing 0,1 m2 dan 0,05
m2. pipa tersebut diletakkan miring. Sehingga
penampang kecil berada 2 m lebih tinggi
daripada penampang besar. Tekanan air pada
penampang kecil adalah 2 .105 Pa. Dan laju air
pada penampang besar 5 m/s. Tentukanlah :
laju air dalam penampang kecil dan tekanan air
pada penampang besar ?
(jawab : 10 m/s ; 2,575 .105 Pa).
Volume air yang melalui pipa per-menit (jawab
: 30 m3)
14. Pesawat terbang modern dirancang untuk
gaya angkat kira-kira 1300 N per m2
penampang sayap. Anggap udara mengalir
melalui sayap sebuah pesawat terbang
dengan garis arus aliran udara. Jika
kecepatan aliran udara yang melalui bagian
yang lebih rendah adalah 100 m/s. Berapa
kecepatan aliran udara di sisi atas sayap
untuk menghasilkan gaya angkat sebesar
1300 N/m2 pada tiap saya. (Massa jenis
udara 1,3 kg/m3). (jawab : 20V30 m/s)
15. Tiap sayap sebuah pesawat terbang
memiliki luas penampang 25 m2. jika kelajuan
udara bagian bawah sayap adalah 50 m/s dan
pada bagian atasnya 70 m/s. Tentukanlah berat
pesawat itu. (anggap pesawat terbang mendatar
pada kelajuan tetap pada ketinggian di mana
massa jenis udara sama dengan 1 kg/m2, juga
anggap semua gaya angkat dihasilkan oleh
kedua sayap). (jawab : 60.000 N).
11.Air mengalir dengan aliran stasioner
sepanjang
pipa
mendapat
yang
luas
penampangnya 20 cm2 pada suatu bagian dan 5
cm2 pada bagian yang lebih sempit. Jika
tekanan pada penampang yang lebih sempit
adalah 4,80 . 104 Pa dan laju alirannya 4 m/s,
Tentuknlah :
Laju aliran (jawab : 1 m/s)
22