Gerbang Logika AND - Dadiek Pranindito

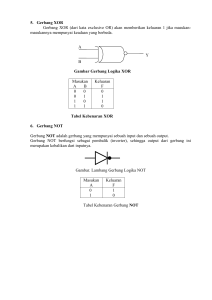
TEKNIK DIGITAL
Submitted by Dadiek Pranindito ST, MT,.
SEKOLAH TINGGI TEKNOLOGI TELEMATIKA TELKOM
PURWOKERTO
LOGO
Review Perkuliahan Sebelumnya
Keterbatasan penyajian data menggunakan sistem bilangan
Penyajian
data
Sistem
bilangan
Sistem
kode
• Operasi Sistem kode dapat menampilkan berbagai jenis data yaitu
bilangan, simbol maupun huruf ke dalam besaran digital
Review Perkuliahan Sebelumnya
• Dalam proses pengolahan, pengiriman dan penerimaan data,
perekaman dan pembacaan data, informasi seringkali dibawa
(dikodekan) dalam bentuk biner / bilangan biner berpola / bit patterns
• Ada beberapa sistem pengkodean yang sering digunakan yaitu :
1. Sistem kode BCD
2. Sistem kode Excess-3
3. Sistem kode Gray
4. Sistem kode ASCII, dll
Contoh Latihan
Kerjakan operasi sistem kode berikut
1.
6839 (10) =.......................(2)=....................... BCD (8421)
2.
137(10) =.......................(2)=....................... BCD (8421)
3.
Tulis dalam bentuk kode XS-3 bilangan desimal 0 ?
4.
Ubah kode XS-3 0111 0001 1010 (XS-3) ke sistem desimal !
5.
Ubah biner 1111 ke dalam gray code?
6.
Ubah desimal 10 ke dalam gray code?
7.
Dengan menggunakan Tabel ASCII, tentukan kode ASCII
untuk “65-M”
8.
Dengan menggunakan Tabel ASCII, tentukan kode ASCII
untuk “st3telkom”
Tujuan Perkuliahan
Mahasiswa dapat memahami dan menjelaskan tentang :
• Analogi Fungsi Logika
• Macam – macam Gerbang Logika
• Penggunaan Tabel Kebenaran
• Penggunaan Rangkaian Logika
Agenda
Chapter 1 – Fungsi Logika
1. Analogi Fungsi Logika
2. Macam – Macam Gerbang Logika
Chapter 2 – Tabel Kebenaran
Chapter 3 – Rangkaian Logika
Analogi Fungsi Logika (1)
Latar Belakang Fungsi Logika
Seperti kita ketahui, mesin-mesin digital hanya mampu mengenali dan mengolah
data yang berbentuk biner. Dalam sistem biner hanya di ijinkan dua keadaan
yang tegas berbeda.
Misal :
• Elemen biner paling sederhana adalah sebuah saklar yang mempunyai 2
keadaan
• x mewakili keadaan dari saklar (s)
• x = 0 saat saklar terbuka/terputus
x = 1 saat saklar tersambung
Analogi Fungsi Logika (2)
Variabel dan Fungsi Logika
Contoh kontrol lampu :
• Keluaran didefinisikan sebagai keadaan dari lampu L
 menyala (hidup) / tidak menyala (mati)
• Keadaan L, sebagai fungsi dari x, yaitu L(x) = x
• Lampu menyala  L=1, lampu mati  L=0
• L(x)
x
adalah fungsi logika,
adalah sebuah variabel masukan
Fungsi Logika AND
Ekspresi dan Operator AND
• Misalnya terdapat 2 saklar untuk mengontrol lampu
• Menggunakan hubungan seri, lampu hanya akan menyala hanya jika
kedua saklar terhubung
Ekspresi fungsi logika AND dari variabel x1dan x2 adalah x1 . x2
L = 1 jika dan hanya jika x1 DAN x2 adalah 1
Operator AND ( . )
x1 . x2 = x1 x2
Rangkaian mengimplementasikan
fungsi logika AND
Gerbang Logika AND
Gerbang AND akan mempunyai output bernilai 1 apabila semua inputnya
bernilai 1, Selain itu outputnya akan bernilai 0.
A
Z
Z = A.B
B
Tabel Kebenaran :
Diagram Venn :
S
A.B
A
B
A
B
A.B
0
0
0
0
1
0
1
0
0
1
1
1
Fungsi Logika OR
Ekspresi dan Operator OR
• Menggunakan hubungan paralel, lampu hanya akan menyala hanya jika
salah satu atau kedua saklar terhubung
Ekspresi fungsi logika OR dari variabel x1dan x2 adalah x1 + x2
L = 1 jika x1 ATAU x2 adalah 1 ( atau keduanya )
Operator OR ( + )
x1 + x2
Rangkaian mengimplementasikan
fungsi logika OR
Gerbang Logika OR
Gerbang OR akan mempunyai output bernilai 0 apabila semua inputnya
bernilai 0, Selain itu outputnya akan bernilai 1
A
Z
Z = A+B
B
Tabel Kebenaran :
Diagram Venn :
S
A
B
A+B
A
B
A+B
0
0
0
0
1
1
1
0
1
1
1
1
Fungsi Logika NOT
Ekspresi dan Operator NOT
• Sebelumnya, lampu menyala saat saklar terhubung. Bagaimana kalau
sebaliknya? Lampu menyala saat saklar terputus
‒
Ekspresi fungsi logika NOT dari variabel x adalah x , x’
L = 1, merupakan invers (komplemen) dari x
‒
Ekspresi : x, x’, NOT x
Rangkaian mengimplementasikan
fungsi logika NOT
Gerbang Logika NOT
Output gerbang NOT adalah kebalikan dari inputnya. Jika input HIGH, maka
output LOW, dan kebalikannya. Gerbang NOT sering disebut INVERTER
A
Z
Diagram Venn :
S
A
A
‒
Z=A
Tabel Kebenaran :
A
A
0
1
1
0
Gerbang Logika NAND
Gerbang NAND merupakan gabungan gerbang AND dan gerbang NOT.
Keluaran gerbang NAND adalah keluaran gerbang AND yang diinversikan
(di-NOT-kan).
A
Z
Z = A.B
B
Diagram Venn :
S
Tabel Kebenaran :
A.B
A
B
A
B
A.B
A.B
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
Gerbang Logika NOR
Gerbang NOR adalah gabungan gerbang OR dan gerbang NOT. Keluaran
Gerbang NOR adalah keluaran gerbang OR diinversikan (di-NOT-kan).
A
Z
Z = A+B
B
Diagram Venn :
S
A
B
A+B
Tabel Kebenaran :
A
B
A+B
A B
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0
Gerbang Logika XOR
Gerbang XOR akan mempunyai nilai output 0 apabila nilai inputnya sama.
A
Z
Z = AB
B
Diagram Venn :
S
A
B
Tabel Kebenaran :
A
B
AB
0
0
0
0
1
1
1
0
1
1
1
0
Agenda
Chapter 1 – Fungsi Logika
Chapter 2 – Tabel Kebenaran
1. Tabel Kebenaran variabel 2
2. Tabel Kebenaran variabel N
Chapter 3 – Rangkaian Logika
Tabel Kebenaran (1)
(Review) Cara merepresentasikan fungsi logika :
Dengan ekspresi fungsi
• Misalnya : A . B adalah ekspresi fungsi AND 2 masukan
• Dua ekspresi yang bernilai sama membentuk persamaan logika
• Misal : z = A . B
Dengan menggunakan tabel kebenaran
• Daftar tabular yang berisi nilai keadaan fungsi untuk semua kombinasi
nilai masukan (perolehan nilai, valuation)
A
B
AND
OR
XOR
0
0
0
0
0
0
1
0
1
1
1
1
1
1
0
1
0
0
1
1
Tabel Kebenaran (2)
Tabel kebenaran dengan 3 variabel
• Tabel kebenaran fungsi AND dan OR 3 variabel : AND-3, OR-3
• Untuk fungsi 3-variabel, terdapat 8 kombinasi masukan
• Untuk fungsi n-variabel, terdapat 2n kombinasi masukan
A
B
C
A.B.C
A+B+C
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Tabel Kebenaran (2) – Gerbang
Logika
Gerbang Dasar dengan Input Lebih Dari 2
• Gerbang AND, OR, NAND dan NOR bisa mempunyai input lebih dari 2 (3,4,
dst)
• Sifat yang dimiliki tetap.
A
B
C
A.B.C
A
B
C
A+B+C
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
1
1
1
1
1
Tabel Kebenaran (3)
Tabel kebenaran suatu fungsi
• Jika Z( A ; B ; C ) = A + BC , maka tabel kebenaran untuk Z adalah
A
B
C
BC
A + BC
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Agenda
Chapter 1 – Fungsi Logika
Chapter 2 – Tabel Kebenaran
Chapter 3 – Rangkaian Logika
1. Rangkaian Logika Sederhana
2. Analisis Pewaktuan
Rangkaian Logika (1)
Definisi Rangkaian Logika
Rangkaian logika tersusun atas gerbang-gerbang logika yang saling
terhubung
• Disebut juga sebagai jaringan logika ( logic network )
• Rangkaian logika ini merupakan bentuk representasi fungsi logika, selain
ekspresi dan tabel kebenaran
Contoh : Gambarkan rangkaian logika untuk fungsi logika L(x1,x2,x3) =
(x1+x2).x3
Contoh Kasus
Gambar rangkaian logika dan isi tabel kebenaran untuk fungsi berikut
Z ( a ; b ; c ) = ac + bc’
Soal Latihan
Gambarkan rangkaian logika dan isi tabel kebenaran dari persamaan logika
1. Z = ab’ + a’b + ab
2. Z = ac + bc’ + a’bc
3. Z = a’bc + ab’c + abc’
Rangkaian Logika (2)
Analisa Pe-waktu-an
• Cara penganalisaan response output terhadap kombinasi input-inputnya
pada periode waktu tertentu
• Peralatan yang digunakan disebut : Timing Diagram (Diagram pe-waktu-an)
Bentuk Timing Diagram :
Contoh Kasus
Buatlah timing diagram untuk mendapatkan output dari gerbang AND
berikut ini :
Jawab :
Soal Latihan
Buatlah timing diagram untuk mendapatkan output dari gerbang Ex-OR
berikut ini
Penutup Perkuliahan
Mahasiswa telah dapat memahami dan menjelaskan
tentang :
• Analogi Fungsi Logika
Fungsi Logika Dengan 2 Masukan
• Macam – macam Gerbang Logika
Gerbang Logika AND, OR, dan NOT
• Penggunaan Tabel Kebenaran
Tabel Kebenaran 2 Masukan, Tabel Kebenaran n Masukan
• Penggunaan Rangkaian Logika
Rangkaian Logika Sederhana, Analisis Pewaktuan
Thank You
Dadiek Pranindito ST. MT.
[email protected]
LOGO
[email protected]