Integral Lipat Dua (Double Integral)

Pertemuan-18 & 19
Integral Lipat Dua
(Double Integral)
Fungsi:
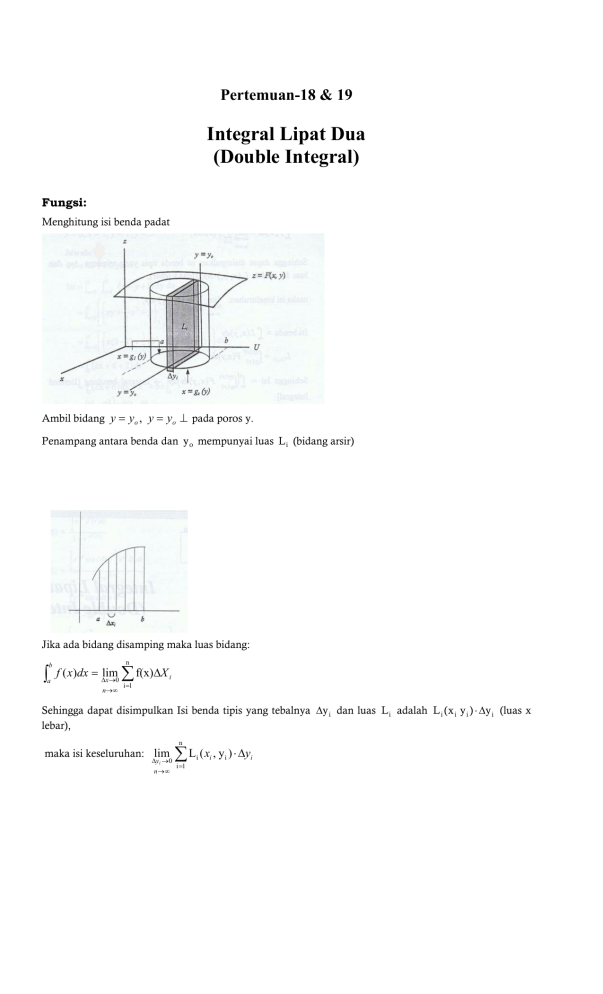
Menghitung isi benda padat
Ambil bidang y = yo , y = yo ⊥ pada poros y.
Penampang antara benda dan y o mempunyai luas L i (bidang arsir)
Jika ada bidang disamping maka luas bidang:
∫
b
a
n
f ( x)dx = lim ∑ f(x)ΔX i
Δx→0
n →∞
i =1
Sehingga dapat disimpulkan Isi benda tipis yang tebalnya Δy i dan luas L i adalah L i ( x i y i ) ⋅ Δy i (luas x
lebar),
n
maka isi keseluruhan: lim
Δyi →0
n→∞
∑ L ( x , y ) ⋅ Δy
i =1
i
i
i
i
Isi benda =
∫
b
a
L( x , y ) = ∫
L( x, y )dy
g2 ( y )
g1 ( y )
F(x, y)dx
⎛⎜ g2 ( y ) F ( x, y )dx ⎞⎟ dy → Integral berulang (Iterated Integral]
∫a ⎝ ∫g1 ( y )
⎠
b
Sehingga Isi =
Isi Benda padat =
b
g2 ( y )
a
g1 ( y )
∫ ∫
F(x, y)dx dy → Double Integral
Contoh:
1.
2
3
∫0 ∫1
2
= ∫0
x 2 ⋅ y dy dx
[∫
3
1
2
]
⎡1
2
x 2 y dy dx = ∫0 x 2 ⎢ y 2
⎢⎣ 2
2
= ∫0 4 x dx = 4 ∫0
2.
π
2
1
∫0 ∫0
2
2
=
0
32
3
x sin y dx dy
π
= ∫0 sin y
[∫ x dx ]dy = 12 ∫
1
π
0
0
1
= − cos y
2
3.
4
x dx = x 3
3
⎤
⎥ dx
1⎥
⎦
3
π
0
sin y dy
=1
Benda padat di bawah bidang z = x + y + 1 dibatasi oleh bidang x = 0, x = 1, y = 1, y = 3
Jawab:
0 ≤ x ≤1; 1≤ y ≤ 3
1
Isi = ∫
x =0
∫
3
y =1
( x + y + 1) dy dx
3
⎡⎧
1 2
⎫ ⎤
+
+
x
y
y
y
⎢⎨
⎬ ⎥ dx
x =0
2
⎩
⎭1 ⎦⎥
⎣⎢
1
=∫
1
=∫
x =0
⎡⎧
1 2 2
⎫⎤
⎢⎨ x(3 − 1) + 2 (3 − 1 ) + (3 − 1)⎬⎥dx
⎭⎦
⎣⎩
= ∫ (2x + 4 + 2) dx
1
0
= ∫ (2x + 6) dx
1
0
(
)
= x 2 + 6x
1
0
= 1 − 0 + 6(1 − 0)
2
2
= 1+ 6 = 7
116
Kalkulus II
4.
x2
5
∫3 ∫− x
( 4 x + 10 y ) dy dx
∫ [(4 xy + 5 y ) ]dx
∫ [4 x( x + x) + 5( x − x )]dx
5
=
2
3
5
=
3
5
∫3 ( 4 x
=
x2
−x
2
3
4
2
+ 4 x 2 + 5x 4 − 5x 2 ) dx
5
1
= ∫ (5 x + 4 x − x ) dx = x + x − x 3
3
3 3
1
= 55 − 35 + 54 − 34 − (53 − 33 )
3
125 − 27
(125 − 27 )
= (3125 − 243) + (625 − 81) −
3
98
= 2882 + 544 −
3
98 10278 − 98 10180
= 3426 −
=
=
3
3
3
5
(
4
) (
= 3393
5.
3
2
5
4
)
1
3
Berikan tafsiran fisis dari
∫∫ ( x
2
+ y 2 ) dx dy , R dibatasi oleh bidang y = x 2 , x = 2 dan y = 1 dan
R
hitunglah integrasinya!
Jawab
Penentuan daerah batas dari gambar di atas, dengan menganggap x konstan/dipegang tetap.
1≤ x ≤ 2
1 ≤ y ≤ x2
Batas di atas dapat pula ditulis dalam y yang konstan
y = x2
x=2
→y = 4
x= y
Integral Lipat Dua
117
1≤ y ≤ 4
y ≤x≤2
Pengintegrasian untuk x yang dipegang konstan.
Batas :
1≤ x ≤ 2
1 ≤ y ≤ x2
2
x2
x =1
y =1
∫ ∫
( x 2 + y 2 ) dy dx
1
= ∫ (x y + y3 )
x =1
3
2
=∫
2
=∫
2
x =1
x =1
x2
2
dx
1
1 6
⎡ 2 2
⎤
⎢ x ( x − 1) + 3 ( x − 1)⎥ dx
⎣
⎦
⎛ 4
x6 1 ⎞
1
1
1
1
⎜⎜ x − x 2 + − ⎟⎟ dx = x 5 + x 7 − x 3 − x
3 3⎠
5
21
3
3
⎝
(
)
(
) (
2
1
)
1 5 5
1 7 7 1 3 3 1
2 −1 +
2 − 1 − 2 − 1 − (2 − 1)
5
21
3
3
32 − 1 128 − 1 8 − 1 1
=
+
−
−
5
21
3
3
=
31 127 7 1 31 127 8
+
− − = +
−
5 21 3 3 5 21 3
651 635 280
=
+
−
105 105 105
=
=
1006
105
Pengintegrasian untuk y dipegang konstan:
Batas:
118
Kalkulus II
1≤ y ≤ 4
y ≤x≤2
4
2
y =1
x= y
∫ ∫
( x 2 + y 2 ) dx dy
⎡⎛ 1
⎞
= ∫ ⎢⎜ x 3 + y 2 x ⎟
y =1
⎠
⎢⎣⎝ 3
2
4
=∫
2
=∫
4
y =1
y =1
⎛1 ⎡ 3
⎜ ⎢2 −
⎝3⎣
⎤
⎥ dy
y⎥
⎦
( y ) ⎤⎥⎦ + y (2 − y )⎞⎟ dy
3
2
⎠
⎛ 8 y3/ 2
⎞
⎜⎜ −
+ 2 y 2 − y 5 / 2 ⎟⎟ dy
3
⎝3
⎠
8
1 1 32 +1
2 2+1
1 52 +1
= y− ⋅ 3
y +
y −5
y
3
3 2 +1
2 +1
2 +1
=
8
2
2
2
y − y 2 y + y3 − y3 y
3
15
3
7
(
) (
4
1
4
1
) (
8
(4 − 1) − 2 42 4 − 12 1 + 2 43 − 13 − 2 43 4 − 13 1
3
15
3
7
8
2
2
2
= (3) − (32 − 1) + (64 − 1) − (128 − 1)
3
15
3
7
=
)
62 126 254 840 434 4410 3810
+
−
=
−
+
−
15
3
7
105 105 105
105
1006
=
105
= 8−
Terlihat bahwa peninjauan x konstan atau y konstan adalah sama, sebab memang daerah yang
dihitung adalah sama.
6.
Hitung
∫∫ x y dx dy
D
Jika D adalah daerah yang dibatasi antara lain y = x ,
y=0 ;x=1
Cara I:
Menentukan batas dengan x dipegang konstan
0 ≤ x ≤1
0≤y≤ x
Integral Lipat Dua
119
1
∫ ∫
0
0
x
1 ⎡
1
xy dy dx = ∫ ⎢ x ⋅ y 2
0
⎢⎣ 2
0
⎤
⎥ dx
⎥⎦
1
x2
dx = x 3
2
6
1
=∫
0
=
x
[
1
0
]
1 3
1
1 − 03 =
6
6
Cara II:
Menentukan batas dengan y dipegang kontans
0 ≤ y ≤1
y2 ≤ x ≤ 1
120
Kalkulus II
1
1
∫
y =0
1
x ⋅ y dx dy = ∫
∫
y2
0
(
)
⎡ 1 2
⎢y ⋅ x
⎣⎢ 2
(
⎤
⎥ ⋅ dy
⎥
y2 ⎦
1
)
y
1 1
1 − y 4 dy = ∫ y − y 5 dy
0 2
2 0
1
⎞
1⎛1
1
= ⎜ y2 − y6 ⎟
⎟
2 ⎜⎝ 2
6
0⎠
1⎛1
1
⎞
= ⎜ (12 − 0 2 ) − 16 − 0 6 ⎟
2⎝2
6
⎠
1
=∫
(
=
)
1 ⎛1 1⎞ 1 ⎛3 1⎞ 1
⎜ − ⎟= ⎜ − ⎟=
2⎝2 6⎠ 2⎝6 6⎠ 6
Dalam mengerjakan soal-soal di atas serta perumusan isi benda padat kita menggunakan koordinat
kartesian.
Macam-macam koordinat yang ada:
1. Koordinat Kartesian
dA = dy ⋅ dx
A = daerah luas
Sehingga
Isi = luas alas . tinggi
n
Isi = lim
ΔA→0
n →∞
Isi =
2.
∫
A
∑ F(x, y) ⋅ ΔA
i =1
F ( x, y )dA = ∫
x
∫
y
F ( x, y )dy dx
Koordinat Polar [silinder]
Integral Lipat Dua
121
dz = ∩ ab =
dϕ
⋅ 2 πr = r dϕ
2π
dA = dr ⋅ dz
dA = dr ⋅ r ⋅ dϕ = r ⋅ dr ⋅ dϕ
∫A
Isi =
3.
F( x, y ) dA = ∫r
∫ϕ
F( x, y ) r ⋅ dϕ dr
Koordinat Umum [Curvilinier Coordinates]
Pada bahasan selanjutnya akan dibuktikan:
dA =
∂ ( x, y )
⋅ du ⋅ dv
∂ (u, v)
Atau
dA =
1
⋅ du ⋅ dv
∂ (u , v)
∂ ( x, y )
Contoh:
1. Tentukan volume bidang Tetrahedron (segi empat) yang dibatasi oleh bidang-bidang koordinat dan
bidang 3x + 6y + 4z = 12 !
Jawab:
Untuk lebih mudah menentukan batas, kita harus gambar bentuk fisisnya:
Langkah menggambar:
z=0
1
3x + 6y = 12 → y = − x + 2
2
122
Kalkulus II
Dibatasi bidang koordinat yang berarti x = 0 dan y = 0
Untuk menentukan z ; x = 0 dan y = 0
4z = 12 → z = 3
fungsi z =
12 − 3x − 6 y
4
batas x dan y untuk x dipegang konstan
0≤x≤4
1
0≤ y ≤− x+2
2
Integral Lipat Dua
123
Isi = ∫
4
x =0
1
− x+2
2
y =0
∫
⎛ 12 − 3x − 6 y ⎞
⎜
⎟ dy dx
4
⎝
⎠
1
3 4 − 2 x+2
(4 − x − 2 y ) dy dx
4 ∫0 ∫0
1
3 4
2 − 2 x+2
dx
= ∫ 4 y − xy − y
0
4 0
2
3 4 ⎡ ⎛ 1
⎞ ⎤
⎞ ⎛ 1
⎞ ⎛ 1
= ∫ ⎢4⎜ − x + 2 ⎟ − x⎜ − x + 2 ⎟ − ⎜ − x + 2 ⎟ ⎥ dx
4 0 ⎣⎢ ⎝ 2
⎠ ⎦⎥
⎠ ⎝ 2
⎠ ⎝ 2
=
(
)
1 2
1 2
3 4 ⎛
⎞
⎜ − 2 x + 8 + x − 2 x − x + 2 x − 4 ⎟ dx
∫
0
4
2
4
⎝
⎠
3 4 ⎛1
⎞
= ∫ ⎜ x 2 − 2 x + 4 ⎟ dx
0
4
⎠
⎝4
4
⎤ 3 ⎡ 64
3⎡1 3
⎤
2
= ⎢ ⋅ x − x + 4 x ⎥ = ⎢ − 16 + 16⎥ = 4
4 ⎣⎢12
⎦
⎥ 4 ⎣ 12
0⎦
=
2.
Hitung volume bagi yang dibatasi oleh bidang-bidang koordinat dan bidang x = 5 dan y + 2z-4=0 !
Jawab:
z=
124
4− y
2
Kalkulus II
Isi = ∫
5
∫
x =0
1 5
⎛4− y⎞
⎜
⎟ dy dx = ∫0
2
⎝ 2 ⎠
4
0
∫
4
0
(4 − y ) dy dx
4
=
1 5
1
1 5
4 y − y 2 dx = ∫ 8 dx
∫
2 0
2
2 0
0
= 4x
3.
5
0
= 4(5 − 0) = 20
Hitung
∫ ∫A
ex
ϕ = 0 dan ϕ =
2
+y2
π
4
dA ; jika A dibatasi oleh r = 1 dan r = 3 ,
!
Jawab:
dA = r dr dϕ
r2 = x2 + y2
1≤ r ≤ 3
π
0≤ϕ≤
4
π /4
3
∫ ∫
1
ex
0
3
2
+ y2
2
0
1
4.
π
3
1
π /4
= ∫ r e r dr ∫
=
dA = ∫
dϕ =
∫
0
π
4∫
e r ⋅ r dr dϕ
3
1
2
r ⋅ e r dr
2
er
π 2
π
d (r 2 ) = e r = (e 9 − e )
2
8
8
1
3
1
Hitung
π /4
3
2
4
∫
∫∫
x 2 + y 2 dA ; jika D adalah bidang yang dibatasi:
D
r = 0dan r sin ϕ , ϕ = 0 dan ϕ = π !
Jawab:
dA = r dr dϕ
0 ≤ r ≤ sin ϕ
0≤ϕ≤π
r = x2 + y2
π
sin ϕ
∫0 ∫0
=∫
π
0
=
π
sin ϕ 2
r ⋅ r dr dϕ = ∫0 dϕ∫0
1 3
r
3
sin ϕ
dϕ =
0
r dr
1 π
sin 3 ϕ dϕ
3 ∫0
π
1
(1 − cos 2 ϕ ) ⋅ sin ϕ dϕ
∫
0
3
1 π
(1 − cos 2 ϕ ) d (cos ϕ )
3 ∫0
1 π
1 π
= − ∫ d (cos ϕ ) + ∫ cos 2 ϕ d (cos ϕ )
3 0
3 0
=−
Integral Lipat Dua
125
π
=
π
1
1
1
+ cos 3 ϕ − (− 1 − 1) + (− 1 − 1)
9
3
9
0
0
1
= − cos ϕ
3
2 2 4
− =
3 9 9
5. Perhatikan gambar
y = r sin ϕ
Hitung
∫∫
!
y dA
s
Jawab:
2 ≤ r ≤ 2 (1 + cos ϕ)
π
2
dA = r ds dϕ
0≤ϕ≤
y dA = ∫
∫∫
π/2
ϕ =0
s
π /2
=∫
0
π /2
=∫
0
π /2
=∫
0
π/2
= ∫0
dϕ ∫
∫
2 (1+ cosϕ )
r =2
2 (1+ cos ϕ )
r =2
sin ϕ dϕ ∫
r ⋅ sin ϕ ⋅ r dr
2 (1+ cos ϕ )
r =2
⎛1
sin ϕ ⎜ r 3
⎜3
⎝
[
y ⋅ r dr dϕ
r 2 dr
2 (1+ cos ϕ )
2
⎞
⎟ dϕ
⎟
⎠
]
sin ϕ
(2 + 2 cos ϕ) 3 − 8 dϕ
3
1 π /2
1 π /2
3
[
2 + 2 cos ϕ ] d (cos ϕ ) − ∫
8 sin ϕ dϕ
∫
3 0
3 0
π
1 1 1
8
4 π
= − ⋅ ⋅ (2 + 2 cos ϕ ) 02 + cos ϕ 02
3 2 4
3
1
(2 + 2 cos π2 )4 − (2 + 2 cos 0)4 + 8 [cos π2 − cos 0]
=−
24
3
1
(2 + 2 ⋅ 0)4 − (2 + 2 ⋅1)4 + 8 [cos π2 − cos 0]
=−
24
3
1 4
8
=−
2 − 4 4 + [0 − 1]
24
3
=−
[{
[{
}]
}]
[
126
]
Kalkulus II
1
[16 − 256] + 8 [− 1]
24
3
240 8
8 30 8 22
=
− = 10 − =
− =
24 3
3 3 3 3
=−
6.
Tentukan Isi benda pada di aktan I dibawah paraboloid z = x 2 + y 2 dan didalam tabung x 2 + y 2 = 9
!
Jawab:
Karena kita tahu
x2 + y2 = r2 = 9
r =3
Isi = ∫∫ z dA
D
π/2
Isi = ∫ϕ = 0
3
∫r = 0
( x 2 + y 2 ) r ⋅ drdϕ
π/2
dϕ∫0 r dr = ∫0
π/2
81
81
ϕ
dϕ =
4
4
= ∫0
= ∫0
3
π/2
3
(
π/2
0
3
1 4
r dϕ
4 0
) = 814 ⋅ 2π = 818π
Soal:
1.
Hitung
∫∫
F ( x) ⋅ ds jika F ( x) = 2 pada 1 ≤ x ≤ 3 dan 0 ≤ y ≤ 2 !
s
Jawab: 8
2.
Gambarkan bagian daerah R di dalam bidang xy yang dibatasi oleh y 2 = 2 x dan y = x !
Cari batas-batas untuk x dan y sehingga tetapkan luas dari R!
Integral Lipat Dua
127
0≤x≤2
, untuk x dipegang tetap
x ≤ y ≤ 2x
Atau untuk y dipegang konstan
0≤y≤2
y2
≤x≤y
2
2
3
Luas =
3.
Hitung isi benda padat dibatasi oleh bidang z = x + y + 1 dan
Jawab: Isi = 7
4.
Hitung isi benda padat antara z = x 2 + y 2 + 2 dan z = 1 dan terletak antara − 1 ≤ x ≤ 1 ,
Jawab: Isi =
5.
Diberikan
∫
3
y =0
∫
4− y
x =1
x = 0, x = 1, y = 1 dan y = 3 .
10
3
( x + y ) dx dy
a.
Gambarkan tafsiran fisis bendanya !
b.
Ubah dalam x dipegang konstan !
Jawab: 1 ≤ x ≤ 2; 0 ≤ y ≤ − x 2 + 9
c.
Hitung Integrasi!
Jawab:
6.
Hitung
∫∫
241
60
x 2 + y 2 dx dy , di mana R adalah bidang daerah x 2 + y 2 ≤ a 2
!
R
Jawab: Dengan koordinat tabung
∫∫
x 2 + y 2 dx dy =
R
7.
2
π a3
3
Hitung isi bidang–4 yang dibatasi bidang-bidang koordinat dan bidang z = 6 – 2x – 3y !
Jawab: Isi = 6
Koordinat Umum (Curvilinier Coordinate)
Sebelum masuk ke pokok bahasan, kita singgung sedikit mengenai vektor.
128
Kalkulus II
0 ≤ y ≤1 !
Aturan-aturan turunan fungsi berlaku untuk turunan vektor
1.
2.
3.
4.
d (A ± B) dA dB
=
±
dt
dt dt
d (A ⋅ B )
dA
dB
=B
+A
dt
dt
dt
⎞ ⎛
d (AxB) ⎛ dA
dB ⎞
= ⎜⎜
x B ⎟⎟ x ⎜⎜ A x
⎟
dt
dt ⎟⎠
⎝ dt
⎠ ⎝
d
du
dA
(u ( t ) ⋅ A ) =
⋅A +u⋅
dt
dt
dt
u(t ) = fungsi skalar
Kita pakai salib sumbu system kanan (aturan tangan kanan)
A = i A x + j A y + k A z = (A x , A y , A z )
B = i B x + j B y + k Bz = (B x , B y , B z )
A • B = (A x , A y , A z )• (B x , B y , Bz )
= A x ⋅ B x + A y ⋅ B y + A z ⋅ Bz
→ [menjadi sekalar]
Aturan Cross Vector (menggunakan kaidah ‘sekrup’]
i x i =0 i x j= k
jx k =i k x i = j
jx j=0 jx i = −k k x j=-i i x k = − j
k x k=0
A x B = (i A x + j A y + k A z ) x ( i B x + j B y + k B z )
= A x B x (i × i ) + A x B y (i × j ) + A x Bz (i × k ) +
A y Bx ( j × i ) + A y B y ( j × j ) + A y Bz ( j × k ) +
A z B x (k × i ) + A z B y (k × j ) + A z Bz (k × k )
Integral Lipat Dua
129
A x B = (i A x + j A y + k A z ) x ( i B x + j B y + k B z )
r
= A x B x 0 + A x B y (k ) + A x Bz (− j ) +
r
A y B x (− k ) + A y B y 0 + A y Bz (i ) +
r
A z B x ( j ) + A z B y (− i ) + A z Bz 0
()
()
()
A x B = i (A y Bz − A z B y ) − j (A x Bz − A z B x ) + k (A x B y − A y B x )
=i
Ay
By
Az
A
−j x
Bz
Bx
Ax
Az
+k
Bx
Bz
Ay
By
Atau dapat ditulis dalam bentuk determinan matriks,
i
A x B = Ax
j
Ay
k
Az
Bx
By
Bz
Koordinat Umum:
130
Kalkulus II
dx
dr
dy
=i
+ j
du
du
du
dx
ds
dy
=i
+ j
dv
dv
dv
d s ds ⎛ dx
dy ⎞ ⎛ dx
dy ⎞
= ⎜i
+ j
+ j ⎟
x
⎟ x ⎜i
du dv ⎝ du
du ⎠ ⎝ dv
dv ⎠
⎛ dx dy ⎞
⎛ dy dx ⎞
=k⎜ ⋅ ⎟−k⎜ ⋅ ⎟
⎝ du dv ⎠
⎝ du dv ⎠
⎛ dx dy dy dx ⎞
=k⎜
−
⋅ ⎟
⎝ du dv du dv ⎠
Harga mutlak:
dr dr
dx dy dy dx
x
=
⋅
−
⋅
du dv
du dv du dv
Dapat dibuat bentuk matrik:
dx
du
dx
dv
dy
du = ∂ ( x, y )
dy
∂ (u , v)
dv
∴ dA =
∂ ( x, y )
du ⋅ dv
∂ (u, v)
Pada rumus di atas terlihat bahwa x dan y harus diubah ke variabel u dan v, perubahan x dan y ke u dan v
tidak selalu mudah, sehingga terkadang lebih mudah mengubah u dan v menjadi x dan y.
Sehingga dalam hal ini kita perlu invers Determinan Jacoby.
∂ ( x, y )
1
didapat dari aturan rantai determinan Jacoby
=
∂ (u , v) ⎛ ∂ (u, v) ⎞
⎜⎜
⎟⎟
⎝ ∂ ( x, y ) ⎠
∴ dA =
du
∂ (u, v)
dx
= du
∂ ( x, y )
dy
1
⋅ du ⋅ dv
∂ (u, v)
∂ ( x, y )
du du
dv
dx = dx dy
dv
dv dv
dy
dx dy
Contoh:
1.
Hitung
∫∫
( x + y ) 3 dx dy ; dengan D adalah bidang yang dibatasi oleh:
D
x+y=3
x + y =1
Integral Lipat Dua
x − y = −1
x−y=2
131
Jawab :
Dengan menggunakan koordinat kartesian sebenarnya kita bisa memecahkannya dengan terlebih dulu
membagi menjadi 3 bagian, dan ini memakan waktu yang lama. Lebih cepat menggunakan koordinat
umum.
Misal:
x + y = u ⎫ 1≤ u ≤ 3
⎬
x − y = v ⎭ −1≤ v ≤ 2
dA =
dx dy
∂ ( x, y )
= du du
dx dy
∂ (u , v)
dv dv
1
1
2 = −1
= 2
1
1
4
−
2
2
dA = −
x+y=u
x−y=v
+
2x = u + v
∂ ( x, y )
⋅ du ⋅ dv
∂ (u , v)
u+v
2
u−v
y=
2
x=
−
1
1
=−
4
2
1
1
du ⋅ dv = du ⋅ dv
2
2
3
∫∫ ( x + y) dxdy = ∫
3
u =1
D
∫
2
v = −1
1
u 3 ⋅ dv du
2
( )
1 3 3
3 3 3
3 43
2
=
=
v
u
du
u
du
u
−1
2 ∫1
8 1
2 ∫1
3
3
= 34 − 14 = [81 − 1] = 30
8
8
=
[
2.
∫∫ ( x
2
]
+ y 2 ) dx dy ; D daerah yang dibatasi
D
132
Kalkulus II
x2 − y2 = 2
x⋅y =1
x⋅y = 3
x2 − y2 = 4
Pada kuadran I
Jawab:
xy = u
x2 − y2 = v
x dan y akan dinyatakan dalam fungsi u dan v.
du
∂ ( x, y )
1
dx
=
= du
∂ (u , v)
⎛ ∂ (u , v) ⎞
⎜⎜
⎟⎟
dy
⎝ ∂ ( x, y ) ⎠
dv
dx = y 2x
dv
x - 2y
dy
= − 2 y 2 - 2x 2 = 2 (x 2 + y 2 )
∂x ⋅ dy =
∫∫ ( x
2
1
⋅ du ⋅ dv
2 (x 2 + y 2 )
+ y2 )
D
1
du ⋅ dv
2 (x + y 2 )
2
[ ]
[ ]
4
1 3
1 3
4
dv ⋅ du = ∫ du ⋅ v 2
∫
∫
2 u =1 v = 2
2 u =1
3
1 3
3
= ∫ du ⋅ (4 − 2) = ∫ du = u 1 = 3 − 1 = 2
u =1
2 u =1
=
Soal:
1.
π
sin θ 2
∫0 ∫0
r dr dθ
Jawab:
4
9
Integral Lipat Dua
133
2.
Tentukan luas dari benda/bidang s, yang adalah daerah di dalam lingkaran r = 4 cos θ dan luar
lingkaran r = z. [Catatan: Transformasikan A =
Jawab: L= 2 3 +
∫∫ dx dy → A =∫∫ r dr dθ
4
π
3
3.
Cari luas daerah yang dibatasi oleh xy = 4, xy = 8, xy 3 = 5 , xy 3 = 15!
Jawab: L= 2 ln 3
4.
Cari luas daerah di dalam kuadran I yang dibatasi oleh y = x 3 , y = 4 x 3 , x = y 3 , x = 4 y 3
Jawab: L=
5.
1
8
Misal R adalah daerah yang dibatasi x + y = 1, x = 0, y = 0.
Perlihatkanlah bahwa:
⎡ (x - y) ⎤
∫∫ cos ⎢⎣ (x + y) ⎥⎦ dx dy =
R
sin 1
2
(Misal x – y = u dan x + y = v}
6.
Benda padat di kuadran I yang dibatasi oleh tabung z = tg x 2 dan bidang-bidang x = y, x = 1 dan y =
0. Cari Isi !
Jawab: Isi =
7.
1
ln sec 1
2
Buktikan:
1
1− x
∫ ∫
x =0 y =0
y
e ( x+ y ) dy dx =
e −1
2
Dengan transformasi x + y = u, y = u.v
Catatan: Soal ini ada baiknya jika dikerjakan sesudah membahas koordinat umum.
8.
Benda dikuadran I yang dibatasi oleh persamaan 9z = 36 − 9x 2 − 4 y 2 dan bidang-bidang koordinat. Cari
Isinya !
Jawab: Isinya = 3π
-oo0oo-
134
Kalkulus II