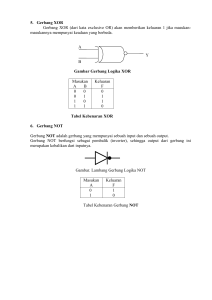
Gerbang Logika dan Rangkaian Logika Kombinasi Disusun Oleh: A. Tujuan 1. Memahami gerbang-gerbang logika AND, OR, NOT, NAND, NOR, EX-OR, EX-NOR. 2. Membuat tabel kebenaran gerbang-gerbang logika. 3. Menyusun rangkaian logika dari gerbang-gerbang logika. 4. Membuat tabel kebenaran dari suatu rangkaian logika berdasarkan percobaan. 5. Menyelidiki cara kerja suatu rangkaian logika 6. Merencanakan rangkaian logika berdasarkan tabel kebenaran dan fungsi-fungsi aljabar Boole. B. Alat Dan Bahan Sumber tegangan DC 5 volt Sumber sinyal digital Gerbang logika Lampu Papan percobaan yang sudah dilengkapi komponen-komponen. Power supply 5 volt DC Kabel-kabel penghubung dan multimeter. IC : SN 7400, SN 7408, SN 7432. C. Dasar Teori Dasar Teori Gerbang Logika Sistim digital hanya mengenal dua keadaan saja, yaitu keadaan tinggi dan keadaan rendah. Untuk logika positif, keadaan rendah mempunyai nilai sekitar 0 volt. dan keadaan tinggi sekitar 5 volt. Keadaan rendah ini dalam sistim digital mempunyai nilai Logika 0 (nol), dan keadaan tinggi mempunyai nilai Logika 1 (satu). Disini untuk selanjutnya kita memakai sistim logika/nalar positif. Lampu didalam sistim digital dikatakan mempunyai nilai logika 1 (satu) bila lampu tersebut menyala/hidup, dan mempunyai nilai logika 0 (nol) bila lampu tersebut padam/mati. Didalam sistem digital hanya ada dua bilangan saja yaitu 1 (satu) dan 0 (nol), sistem bilangan yang dipakai sistem bilangan biner. Dalam praktikum digunakan komponen-komponen yang sudah dalam bentuk IC /Chip yaitu suatu alat yang memadukan rangkaian yang terdiri dari beberapa 1 komponen elektronika dalam satu kemasan. Pada dasarnya didalam sistem digital hanya ada tiga gerbang logika. Gerbang-gerbang yang lain dapat disusun dari ketiga gerbang tersebut yaitu AND, OR, dan NOT. Secara keseluruhan ada 7 (tujuh) fungsi logika yang ada didalam sistem digital yaitu: AND, OR, NOT, NAND, NOR, EX-OR, EX-NOR. 1. Gerbang NOT (NOT gate) NOT gate ini juga dinamakan INVERTER, mempunyai satu input dan satu output. Lambang gerbang NOT dan tabel kebenarannya disajikan pada gambar 1 dan tabel 1 di bawah. 2. Gerbang AND (AND gate) AND gate mempunyai dua input atau lebih dan hanya mempunyai satu output saja. Operasi logikanya adalah operasi perkalian. Y=A.B....N Lambang gerbang AND dan tabel kebenarannya disajikan pada gambar 2 dan tabel 2 di bawah. 2 Dari tabel kebenaran di atas tampak bahwa outputnya dalam keadaan 1 (satu) hanya apabila semua inputnya dalam keadaan 1 (satu), dan outputnya 0 (nol) apabila salah satu inputnya 0 (nol). Tanpa memandang nilai-nilai input yang lain, apabila salah satu inputnya 0 (nol), nilai outputnya pasti 0 (nol). 3. Gerbang OR (OR gate). OR gate mempunyai dua input atau lebih dan hanya mempunyai satu output saja. Operasi logika gerbang ini merupakan operasi penjumlahan dapat dituliskan dalam bentuk: Y = A + B + .............. N Lambang gerbang OR dan tabel kebenarannya disajikan pada gambar 3 dan tabel 3 di bawah. Dari tabel kebenaran di atas tampak bahwa Outputnya dalam keadaan 0 (nol) hanya apabila semua inputnya dalam keadaan 0 (nol). 3 4. Gerbang NAND (NAND gate) NAND gate mempunyai dua input atau lebih dan satu input saja. NAND gate terdiri dari AND gate dan NOT gate. Lambang gerbang NAND disajikan pada gambar 4 di bawah. Berdasarkan sifat-sifat gerbang AND dan NOT dapat diselidiki sendiri cara kerja gerbang NAND. Demikian juga dapat dibuat/disusun tabel kebenaran untuk NAND gate yang mempunyai dua input. Nilai outputnya dapat dituliskan: 5. Gerbang NOR (NOR gate) NOR gate mempunyai dua input atau lebih dan hanya mempunyai satu input saja. NOR gate ini terdiri dari gerbang OR dan gerbang NOT. Lambang gerbang NORdisajikan pada gambar 5 di bawah. Berdasarkan sifat-sifat gerbang AND dan NOT dapat diselidiki sendiri cara kerja gerbang NAND. Demikian juga dapat dibuat / disusun tabel 4 kebenaran untuk NAND gate yang mempunyai dua input. Nilai outputnya dapat dituliskan: Berdasarkan sifat-sifat gerbang OR dan geerbang NOT dapat diketahui cara kerja gerbang NOR. Demikian pula dapat dibuat tabel kebenarannya NOR gate yang terdiri dari dua input. 6. Gerbang EX-OR (OR khusus). EX-OR gate mempunyai dua input atau lebih dan hanya mempunyai satu output saja. Lambang gerbang EX-OR dan tabel kebenarannya disajikan pada gambar 6 dan tabel 4 di bawah. Operasi ini merupakan perkalian komplemen salah satu input dengan input yang lainnya dan sebaliknya dan kemudian dijumlahkan. Untuk dua input A dan B: Cara kerja gerbang ini dapat diselidiki dengan cara memasukkan berbagai nilai input dan menentukan outpuntya. 5 7. Gerbang EX-NOR (NOR khusus). EX-NOR gate mempunyai dua input atau lebih dan hanya mempunyai satu output saja. Gerbang ini terdiri dari EX-OR gate dan NOT gate. Lambang gerbang EX-NORdisajikan pada gambar 7 di bawah. Output gerbang ini dapat dituliskan dalam bentuk : Berdasarkan sifat-sifat gerbang EX-OR dan NOT diketahui cara kerja gerbang EX-NOR. Demikian juga dapat dibuat tabel kebenaran untuk gerbang EX-NOR yang terdiri dari dua input. Nilai-nilai tinggi 1 (satu) dan rendah 0 (nol) tersebut dalam batas-batas tertentu seperti pada gambar 8. 6 Dasar teori Gerbang Logika Kombinasi Rangkaian-rangkaian logika digolongkan/dikelompokkan menjadi dua kelompok besar. Kelompok pertama kita sebut rangkaian logika kombinasi. Dan kelompok kedua kita sebut rangkaian logika sekuensial/berurutan. Suatu rangkaian kombinasi terdiri dari gerbanggerbang logika yang keluarannya (outputnya) tak tergantung pada masukkan sebelumnya. Rangkaian kombinasi melakukan pengolahan informasi tertentu yang ditentukan secara logika oleh suatu himpunan fungsi Boole. Pada rangkaian berurutan/sekuensial keluarannya tergantung pada masukkan pada saat itu dan masukkan pada saat sebelumnya. Perilaku rangkaian urutan itu tergantung pada urutan masukkan menurut waktu dan keadaan dalam rangkaian itu. Rangkaian berurutan/sekuensial mempunyai ingatan (memori), penyusun rangkaian utama ini terdiri dari Flip-Flop. Contoh rangkaian sekuensial adalah counter/pencacah, register dsb. Perencanaan/desain rangkaian logika. Perencanaan rangkaian logika ini berawal dari uraian yang dinyatakan dengan kata-kata untuk suatu masalah, kemudian diterjemahkan dalam suatu himpunan fungsi Boole yang dapat diimplementasikan ke suatu rangkaian logika. Masalah-masalah itu misalnya gejala fisis yang dapat diamati maupun yang tak dapat diamati oleh indera kita, gejala mekanis dan gejala-gejala alam yang lainnya. Dalam mendesain/merencanakan rangkaian logika itu diperlukan syarat-syarat sebagai berikut ini : 7 Banyaknya gerbang logika diusahakan sesedikit mungkin. Jumlah masukkan/input sesuatu gerbang diusahakan minimum/minimal. Sinyal data/informasi yang menjalar sepanjang rangkaian diusahakan memakan waktu sesingkat mungkin. Interkoneksi/sambungan-sambungan sesedikit/sesingkat mungkin. Semua pernyataan-pernyataan di atas tentunya sulit untuk dipenuhi. Pada umumya penyederhanaan itu bermula dari tujuan dasarnya yaitu menghasilkan fungsi Boole sederhana dalam bentuk baku. Dalam hal ini aljabar Boole berperanan sekali untuk menjelaskan serta menyederhanakan rangkaian-rangkaian logika. Pada rumus-rumus di atas hanya ada dua operasi aritmatika yaitu penjumlahan dan perkalian. Teorema De Morgan dapat dilihat pada rumus 16 dan 17. Rumus ini menunjukkan bahwa operasi penjumlahan dapat diubah menjadi operasi perkalian; dan sebaliknya operasi perkalian dapat diubah menjadi operasi penjumlahan 8 Pemakaian Teorema De Morgan Contoh: Untuk gerbang EX-OR diketahui fungsi logika Ubahlah bentuk penjumlahan tersebut menjadi bentuk perkalian Dilihat dari bentuk diatas, rangkaian ini EX-OR dapat dibentuk dengan gerbang NAND seperti pada gambar 1. 9 Dari rumus fungsi logika dan tabel kebenarannya, dapat disimpulkan bahwa rangkaian di atas ekivalen dengan gerbang EX-OR. Jadi satu fungsi logika dapat disusun oleh berbagai-bagai gerbang logika sehingga mempunyai nilai output yang sama. Seperti fungsi logika pada rangkaian di atas dapat pula disusun oleh gerbang-gerbang logika yang lainnya. Terdapat beberapa metode untuk merancang/mendesain rangkaian logika. Untuk bentuk-bentuk sederhana dipakai metode Sum of Products (jumlah hasil kali) dan Products of Sum (hasil kali jumlah). Prosedur umum memperoleh bentuk sum of products (S of P) dari suatu tabel kebenaran adalah sebagai berikut.: Tulislah dalam bentuk AND (perkalian logika) untuk setiap kasus didalam tabel kebenaran dimana outputnya bernilai 1 (satu) Sederhanakan bentuk itu dengan menggunakan rumus-rumus dalam aljabar Boole/pakai metode peta Karnaugh. Semua bentuk AND kemudian di-OR-kan (dijumlahkan) menjadi satu untuk memperoleh ekspresi output akhir. Contoh : Buat rangkaian logika yang punya tiga input A,B dan C. Outputnya hanya tinggi (1) apabila mayoritas inputnya bernilai satu. a. Penyelesaian: Metode Sum of Products Buat tabel kebenarannya seperti dibawah ini. 10 Dari persamaan di atas, dapat dibentuk rangkaian seperti pada gambar 2. Gambar 2. Rangkaian logika dalam bentuk Sum of Products Y = AB + BC + AC b. Penyelesaian: Metode Products of Sum Prosedur umum untuk mendapatkan ekspresi dari tabel kebenaran dalam bentuk Products of Sum. Bagian output pada tabel kebenaran itu diinversikan (di NOT kan), Kemudian tuliskan dalam bentuk Sum of Products. Sederhanakanlah bentuk output tersebut. 11 Inversikan ekpresi tersebut untuk mendapatkan Y (output) Dari persamaan di atas, dapat dibentuk rangkaian seperti pada gambar 3. 12 D. Prosedur Percobaan Gerbang Logika 1. Untuk gerbang logika NOT. a. Buatlah rangkaian di multisim seperti pada gambar berikut ini. b. Amatilah outputnya untuk berbagai nilai input. Catatlah hasilhasil percobaan ini dalam bentuk tabel seperti contoh di bawah. Tabel hasil pengamatan Gerbang logika:...... Input Output Keadaan lampu Bentuk biner 0 1 2. Untuk gerbang logikan lain dengan dua input (AND, OR, NAND, NOR, EX-OR, EX-NOR). a. Buatlah rangkaian di multisim seperti pada gambar berikut ini. 13 b. Amatilah outputnya untuk berbagai nilai input. Catatlah hasil hasil percobaan ini dalam bentuk tabel seperti contoh di bawah. c. Lakukan untuk semua gerbang logika. Tabel hasil pengamatan Gerbang logika : .............. Input Output A B Keadaan lampu Bentuk biner 0 0 0 1 1 0 1 1 3. Untuk gerbang logikan lain dengan tiga input (AND, OR, NAND, NOR, EX-OR, EX-NOR) a. Buatlah rangkaian di multisim seperti pada gambar berikut ini. b. Amatilah outputnya untuk berbagai nilai input. Catatlah hasilhasil percobaan ini dalam bentuk tabel seperti contoh di bawah. c. Lakukan untuk semua gerbang logika. Tabel hasil pengamatan Gerbang logika : .............. Input Output A B C Keadaan lampu Bentuk biner 0 0 0 14 0 0 0 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 1 0 1 Gerbang Logika Kombinasi\ I. Gerbang EX-OR dari gerbang NAND 1. Buatlah rangkaian seperti yang ditunjukkan oleh gambar 1. Output akhir diganti dengan lampu (jangan lupa hubungkan lampu dengan ground). 2. Berikan beberapa kombinasi input pada rangkaian percobaan ini, amatilah nilai outputnya. 3. Catatlah hasil percobaan ini dalam bentuk tabel. Input Output A B Keadaan lampu Bentuk biner 0 0 0 1 1 0 1 1 4. Bandingkanlah hasil percobaan ini dengan tabel kebenaran untuk masing-masing rangkaian logika. II. Rangkaian logika dengan tiga input\ 1. Buatlah rangkaian seperti yang ditunjukkan gambar 2. 2. Lakukanlah langkah-langkah percobaan seperti pada percobaan yang telah terdahulu. 3. Catatlah hasil-hasil percobaan dalam bentuk tabel. Input Output 15 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Keadaan lampu Bentuk biner 4. Bandingkanlah hasil percobaan ini dengan tabel kebenaran untuk masing-masing rangkaian logika. 5. Lakukang langkah 1-4 untuk rangkaian yang ditunjukkan oleh gambar 3. E. Kesimpulan F. Daftar Pustaka 1. Santosa,Ign Edi.Eksperimen Fisika Edisi 2.Laboratorium Fisika Universitas Sanata Dharma Yogyakarta.2017. 2. Karakteristik Dioda Semikonduktor Daring.pdf link:https://belajar.usd.ac.id/pluginfile.php/421069/mod_resource/con tent/1/%5B4%5D%20Karakteristik%20Dioda%20Semikonduktor%20 -%20Daring.pdf 16