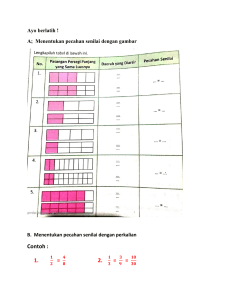
Tugas Makalah KAPITA SELEKTA MATEMATIKA PENDIDIKAN DASAR “MISKONSEPSI SISWA PADA KONSEP DASAR PECAHAN” Di Ajukan Untuk Memenuhi Tugas Kapita Selekta Pendidikan Dasar Yang Di Ampu Oleh Saleh, S.pd. M.pd Oleh Kelompok VIII: Adim Jufriyatno Syarifudin (A1I119019) Arni Rahmayanti (A1I119069) Muhammad Fitrah Ramadhan (A1I119047) Syarif Hidayatullah (A1I119091) JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS HALU OLEO KENDARI 2020 KATA PENGANTAR Assalamu’alaikum warahmatullahi wabarakatuh Segala puji bagi Allah SWT yang telah memberikan penulis kemudahan dalam menyelesaikan makalah tepat waktu. Tanpa rahmat dan pertolongan-Nya, penulis tidak akan mampu menyelesaikan makalah ini dengan baik. Tidak lupa shalawat serta salam tercurahkan kepada Nabi agung Muhammad SAW yang syafa’atnya kita nantikan kelak. Penulis mengucapkan syukur kepada Allah SWT atas limpahan nikmat sehatNya, sehingga makalah “miskonsepsi siswa terhadap konsep dasar pecahan” dapat diselesaikan. Makalah ini disusun guna memenuhi tugas mata kuliah Kapita Selekta Matematika Pendidikan Dasar. Penulis berharap makalah tentang miskonsepsi siswa terhadap konsep pecahan ini dapat menjadi referensi bagi bagi guru maupun siswa agar dapat meminimalisir terjadinya miskonsepsi dalam proses belajar dan mengajar. Penulis menyadari makalah bertema miskonsepsi ini masih perlu banyak penyempurnaan karena kesalahan ataupun kekurangan. Penulis terbuka terhadap kritik dan saran pembaca agar makalah ini dapat lebih baik. Apabila terdapat banyak kesalahan pada makalah ini, baik terkait penulisan maupun konten, penulis memohon maaf. Demikian yang dapat penulis sampaikan. Akhir kata, semoga makalah ini dapat bermanfaat. Wassalamu’alaikum warahmatullahi wabarakatuh i DAFTAR ISI COVER KATA PENGANTAR ................................................................................................................... i DAFTAR ISI ................................................................................................................................. ii BAB I ............................................................................................................................................ 1 PENDAHULUAN......................................................................................................................... 1 1.1 Latar Belakang .............................................................................................................. 1 1.2 Rumusan Masalah ......................................................................................................... 3 1.3 Tujuan Penulisan ........................................................................................................... 4 1.4 Manfaat Penulisan ......................................................................................................... 4 BAB II ........................................................................................................................................... 5 KAJIAN PUSTAKA ..................................................................................................................... 5 2.1 Pemahaman Konsep ...................................................................................................... 5 2.2 Pecahan ......................................................................................................................... 6 2.3 Alat Peraga Blok Pecahan ............................................................................................. 7 BAB III........................................................................................................................................ 10 PEMBAHASAN ......................................................................................................................... 10 3.1 Miskonsepsi Siswa ...................................................................................................... 10 3.2 Alat Peraga Blok Pecahan ........................................................................................... 14 BAB IV ....................................................................................................................................... 18 PENUTUP ................................................................................................................................... 18 4.1 Kesimpulan ................................................................................................................. 18 4.2 Saran............................................................................................................................ 18 DAFTAR PUSTAKA ................................................................................................................. 19 LAMPIRAN ................................................................................................................................ 20 ii BAB I PENDAHULUAN 1.1 Latar Belakang Salah satu konsep dasar matematika yang diajarkan semenjak sekolah dasar (SD) adalah konsep pecahan. Sepintas, konsep matematika yang diberikan pada siswa SD sangatlah sederhana dan mudah. Namun, faktanya hasil penelitian Maria Endah Savitri beserta rekan-rekannya menunjukkan bahwa masih ditemukan siswa kelas VIII yang keliru dalam memahami konsep pecahan dalam bentuk aljabar dan kekeliruan itu disebabkan oleh kurangnya pemahaman siswa pada konsep pecahan (Savitri, dkk, 2016:403). Beberapa penelitian sebelumnya juga menunjukan bahwa pengetahuan siswa pada operasi bilangan bulat dan pecahan masih menjadi hambatan dalam menyelasaikan masalah pada materi 2 aljabar (Steinle dkk, 2009:492, Herutomo dan Saputro, 2014:174). Hal tersebut didukung pula oleh pendapat Theis (2013:13) bahwa banyak materi matematika SD yang belum dipahami siswa ataupun mahasiswa dengan baik, diantaranya materi pecahan (konsep dasar, operasi dan pemacahan masalahnya). Padahal, konsep pecahan menjadi materi prasayarat pada materi matematika lanjutan seperti Sistem Persamaan dan Pertidakasamaan Linear, Perbandingan, Aritmatika Sosial, Peluang, dan sebagainya. Oleh karena itu konsep pecahan perlu mendapat perhatian khusus. Pada materi pecahan di tingkat SD masih mempelajari hal-hal yang sangat sederhana seperti mempelajari simbol dan menuliskan bentuk bilangan pecahan, menyajikan pecahan kedalam bentuk gambar maupun sebaliknya, bagaimana letak pembilang dan penyebut pecahan, membandingkan dan mengurutkan nilai pecahan, hingga tingkatan yang lebih tinggi pada materi pecahan tingkat SD yaitu operasi dan pemecahan masalahnya. Namun pada proses belajar mengajar dikelas kenyataannya banyak siswa yang kesulitan dalam mencapai kompetensi tersebut, masih banyak siswa yang mengalami 1 miskonsepsi contohnya siswa miskonsepsi menerjemahkan atau menetukan mana pembilang dan mana penyebut dari sebuah gambar sehingga seringkali terbalik dalam penulisannya. siswa juga miskonsepsi saat mengurutkan dan membandingkan nilai yang terbesar atau terkecil dari beberapa bilangan pecahan yang diberikan karena hanya melihat angka terbesar di antara bilangan pecahan tersebut meskipun angka itu terletak sebagai penyebut. selain itu siswa juga kesulitan menggambarkan bentuk pecahan karena tidak mengetahui konsep sebenarnya bagaimana bilangan pecahan itu bisa terbentuk dan lain-lain. Berbagai miskonsepsi tersebut disebabkan karena kurangnya pemahaman konsep pecahan oleh siswa. contoh yang paling dasar ialah konsep pecahan sebagai bagian dari keseluruhan, dimana pembilang menyatakan bagian yang dimaksud dan penyebut menunjukkan jumlah bagian yang dipertimbangkan. Saat siswa tidak memahami konsep tersebut maka siswa akan miskonsepsi saat menunjukkan bentuk bilangan pecahan dari sebuah gambar. Contoh lain yaitu ketika siswa tidak memahami konsep pecahan sebagai bagian dari suatu daerah yang bagian-bagiannya kongruen, maka siswa akan miskonsepsi karena menggambarkan bagian-bagian daerah pecahan yang tidak kongruen dll. Sangat penting untuk mempelajari dan memahami konsep pecahan karena pecahan juga merupakan dasar dari berbagai macam materi dalam matematika. jika konsep awal yang dipelajari siswa salah atau bahkan tidak mengetahui konsepnya maka untuk penerapan konsep itu pada pengetahuan selanjutnya akan salah juga dan hal tersebut akan menimbulkan berbagai kesalahan. Pecahan menjadi landasan bagi siswa dalam mempelajari matematika selanjutnya seperti persen, rasio, dan aljabar. Bahkan operasi dan aplikasi dari bilangan pecahan berhubungan dengan kehidupan nyata dan digunakan di dalamnya. Solusi dalam menyikapi sulitnya siswa dalam memahami konsep bilangan yaitu diperlukan suatu metode pembelajaran yang menarik dan bermakna agar siswa aktif ikut terlibat didalam memahami materi pembelajaran. Untuk Anak usia sekolah dasar yang belum mampu memahami operasi logis 2 dari konsep matematika, diperlukan alat peraga dalam proses belajar-mengajar agar ilmu yang disampaikan dapat diserap dengan mudah dan mengingatnya lebih lama. Sesuai dengan pandangan Dienes ( Ruseffendi, 1992:204 ) yang mengemukakan “ tiap-tiap konsep atau prinsip dalam matematika yang disajikan dalam bentuk konkret akan dapat dipahami dengan baik “. menerangkan konsep pecahan pada siswa sekolah dasar harus selalu diawali dengan menggunakan benda konkret. Oleh sebab itu dalam pembuatan makalah penelitian ini saya menggunakan alat peraga blok pecahan dalam upaya meningkatkan pemahaman siswa tentang konsep pecahan. alat peraga blok pecahan saya buat sendiri menggunakan kardus dan kertas berwarna yang tentunya aman bagi siswa. Selain itu, alasan saya memilih alat peraga blok pecahan dalam mengajarkan konsep pecahan adalah dapat memperjelas konsep matematika dalam bentuk nyata, bentuk dan warnanya menarik, mudah digunakan siswa karena mudah di pegang, dipindahkan, dipasangkan, dan sebagainya, dan yang terakhir bentuknya yang lingkaran memudahkan pengajar untuk memotong dan membagi lingkaran tersebut menjadi beberapa bagian dan cocok untuk digunakan menjelaskan konsep pecahan. 1.2 Rumusan Masalah 1. Bagaimana miskonsepsi yang dilakukan siswa terhadap konsep dasar pecahan ? 2. Mengapa siswa mengalami miskonsepsi terhadap konsep dasar pecahan ? 3. Bagaimana penggunaan alat peraga blok pecahan untuk mengatasi miskonsepsi siswa terhadapkonsep dasar pecahan ? 3 1.3 Tujuan Penulisan 1. Untuk mengetahui bagaimana miskonsepsi yang dilakukan siswa terhadap konsep dasar pecahan 2. Untuk mengetahui mengetahui mengapa siswa mengalami miskonsepsi terhadap konsep dasar pecahan 3. Untuk mengetahui bagaimana penggunaan alat peraga blok pecahan untuk mengatasi miskonsepsi siswa terhadapkonsep dasar pecahan 1.4 Manfaat Penulisan Manfaat yang diharapkan dalam pembuatan makalah ini adalah : 1. Bagi guru matematika, makalah ini dapat dijadikan sebagai referensi untuk mengetahui gambaran letak miskonsepsi siswa pada konsep bilangan pecahan. Sehingga dapat dirancang strategi pengajaran yang efektif untuk menunjang hasil belajar yang diharapkan. 2. Bagi siswa, sebagai bahan masukan untuk memperbaiki miskonsepsi pada konsep bilangan pecahan sehingga dapat meningkatkan prestasi belajar siswa. 3. Bagi akademisi dan peneliti lain, dapat digunakan sebagai bahan sumbangan pemikiran dan referensi mengenai miskonsepsi yang dialami siswa dengan gaya kognitif field dependence pada konsep bilangan pecahan. 4 BAB II KAJIAN PUSTAKA 2.1 Pemahaman Konsep Inti dalam pembelajaran matematika adalah pemahaman mengenai konsep. Godino (2015: 2) mendefinisikan pemahaman sebagai pengalaman mental dari suatu subjek, dimana melalui pengalaman tersebut subjek dapat menghubungkan suatu objek dengan objek lain mengguanakan inderanya. Dalam pembelajaran matematika, istilah “pemahaman” juga digunakan dalam proses penilaian atau evaluasi siswa. Seberapa siswa dapat menguasai konsep dilihat dari seberapa siswa mampu memahami konsep tersebut. Hal ini sejalan dengan pendapat Skemp (2002: 47), menurutnya pemahaman adalah menghubungkan pengalaman atau ide baru dengan skema yang sudah ada. Pemahaman akan meluas seiring beradaptasi dengan situasi yang baru, sehingga pemahaman itu penting untuk mempelajari matematika. Hasil temuan Geller, Son, & Stigler (2017: 122) menunjukkan bahwa siswa yang lemah pemahamannya memiliki kecenderungan berfokus pada hal konkrit, siswa yang lebih kuat cenderung menggunakan konsep untuk menjelaskan jawabannya, sedangkan siswa dengan pemahaman yang tinggi cenderung menggunakan konsep yang lebih umum. Hal ini berimplikasi pada pendekatan dalam pembelajaran matematika. Ketika mengenalkan konsep, diasumsikan pemahaman siswa masih rendah, sehingga memerlukan hal-hal konkrit untuk menurunkan tingkat keabstrakan konsep matematika. Hal ini sejalan dengan pendapat D’Agustin & Smith (1992: 2), bahwa pembelajaran matematika dapat ditingkatkan jika ada perubahan yang dibuat bukan hanya dalam kurikulum, tetapi juga dalam cara mengajarkan matematika pada siswa. Matematika adalah pemahaman terhadap konsep-konsepnya. Kabbach & Fadel (2014: 4) mendefinisikan konsep adalah gagasan/ide abstrak. Konsep terletak pada pemikiran manusia. Konsep matematika adalah pemikiran atau sudut pandang manusia terhadap matematika itu sendiri. Souviney (1994: 34) 5 mendefinisikan konsep matematika sebagai pola dasar yang menghubungkan kumpulan objek atau tindakan satu sama lain. Terdapat fakta-fakta dasar dalam matematika. Ketika fakta tersebut saling berkaitan oleh suatu kondisi, maka akan menjadi sebuah konsep yang utuh. 2.2 Pecahan Pecahan atau fraction secara terminologi, menurut Bennett, Burton, & Nelson (2010: 283) berasal dari bahasa latin fractio dari bentuk frangere yang berarti jeda. Secara historis, pecahan pertama kali digunakan untuk mewakili jumlah yang kurang dari satu atau satu kesatuan, seperti setengah permen, sepertiga pizza, dan lainnya. Pecahan sebagai materi memiliki beberapa definisi. Novak & Renzo (2013: 3) berpendapat bahwa pecahan merupakan sebuah hasil bagi atau representasi bagian dari angka. Hal ini sebagai penguat konsep pecahan sebagai pembagian. Selain itu, menurut Musser, Burger, & Peterson (2011: 216) pecahan dapat dimaknai dengan dua cara yang berbeda. Pertama, pecahan digunakan sebagai angka yang menunjukkan bagian dari keseluruhan. Kedua, pecahan dimaknai sebagai perbandingan. Bennett, et al. (2010: 283) mengilustrasikan pecahan menjadi tiga konsep, yaitu konsep pecahan sebagai bagian dari keseluruhan, konsep pecahan sebagai hasil bagi, dan konsep pecahan sebagai rasio. Pecahan sebagai bagian dari keseluruhan, pada bilangan pecahan terdiri dari pembilang yaitu bilangan yang terletak di atas dan penyebut yaitu bilangan yang terletak di bawah. Pembilang menunjukkan jumlah keseluruhan yang dimaksud. Penyebut menunjukkan jumlah bagian yang dipertimbangkan. Kedua bilangan tersebut dipisahkan oleh sebuah garis. Definisi pecahan sebagai bagian dari keseluruhan juga digunakan pada konsep pecahan sebagai bagian dari sekumpulan (set). Pecahan sebagai hasil bagi, pecahan muncul dari pembagian antara suatu bilangan dengan bilangan yang lain. Dapat disimbolkan pembilang sebagai bilangan yang terbagi, penyebut sebagai bilangan pembagi. Pecahan dapat didefinisikan sebagai konsep rasio. Dalam definisi ini, pecahan digunakan untuk membandingkan satu jumlah dengan jumlah yang lain. Pada simbol pecahan dapat dibaca sebagai perbandingan antara pembilang dengan penyebut. 6 Hasil penelitian Ciosek & Samborska (2015: 10) menyimpulkan bahwa pecahan adalah topik yang sangat sulit. Temuan menunjukkan banyak kesalahan siswa yang mengindikasikan kurangnya pemahaman konsep siswa pada pecahan. Hal ini sejalan dengan temuan Stringler, Givvin, & Thompson (2010: 4), menunjukkan bahwa pecahan sangat sulit dipahami siswa. Meskipun materi ini telah diajarkan sejak kelas 3, namun banyak siswa lulusan sekolah menengah masuk perguruan tinggi masih memiliki pemahaman bilangan rasional yang dangkal. Rendahnya pemahaman konsep pecahan tersebut berdasarkan temuan Siegler & Pyke (2013: 1994) disebabkan siswa belajar dengan menghafal aturan prosedural, tanpa memahami konsep-konsep yang sesuai dengan pecahan, sehingga banyak aturan operasional yang tidak dimengerti. Hal ini menjadikan asumsi bahwa pecahan merupakan representasi matematika. temuan dari Torbeyns, et al. (2015: 5) bahwa pemahaman siswa tentang pecahan berhubungan positif terhadap prestasi matematika siswa secara umum. Dengan kata lain, jika siswa telah memahami konsep pecahan, maka konsep matematika selain pecahan juga bisa dipahaminya. Untuk itu,guru hendaknya mendesain pembelajaran yang sesuai sehingga tujuan dapat tercapai. Sebagaimana hasil temuan Hurrell (2013: 2) yang mengindikasikan bahwa pembelajaran yang terstruktur dengan baik akan berdampak positif terhadap kepercayaan diri guru dalam mengajarkan topik matematika yang sulit seperti pecahan. 2.3 Alat Peraga Blok Pecahan Menurut Annisah(2014), matematika tidak mudah dipahami oleh sebagian siswa khususnya siswa SD/MI. Untuk mempelajari objek matematika yang abstrak diperlukan jembatan atau perantara yang bersifat konkrit. Model benda nyata yang digunakan untuk mengurangi keabstrakan materi matematika disebut alat peraga pembelajaran matematika. Hasil wawancara peneliti dengan guru kelas V di SD negeri Bejirejo, materi yang mengalami kesulitan antara lain, bangun ruang, pecahan, dan perbandingan. Materi pecahan dianggap sulit karena siswa kurang memahami konsep pecahan dan materi ini dipelajari sejak kelas III. 7 Menurut Ahmadin Sitanggang (2013), alat peraga matematika adalah sebuah atau seperangkat benda konkrit yang dibuat, dirancang, dihimpun atau disusun secara sengaja, yang digunakan untuk membantu menanamkan atau mengembangkan konsep-konsep atau prinsip-prinsip dalam matematika. Menurut Estiningsih dalam Sukayati dan Agus Suharjana (2009), alat peraga merupakan media pembelajaran yang mengandung atau membawakan ciriciri konsep yang dipelajari. Sudarwanto dan Ibnu Hadi(2014), alat peraga pembelajaran adalah bahan, alat, maupun metode/teknik yang digunakan dalam kegiatan belajar mengajar dengan maksud agar proses interaksi komunikasi edukatif antara guru dan anak didik dapat berlangsung secara efektif dan efisien sesuai dengan tujuan pengajaran yang dicita-citakan. Dari pengertian para ahli, maka dapat disimpulkan bahwa alat peraga adalah bahan, alat atau seperangkat benda konkrit yang membawakan ciri-ciri konsep yang dipelajarinnya serta mempermudah komunikasi antara guru dan anak didik. Salah satu media pembelajaran yang dapat dipakai pada masalah konsep pecahan yaitu alat peraga blok pecahan. Blok Pecahan berbentuk dasar lingkaran, bisa dibagi sesuai dengan pecahan yang diinginkan. Fungsinya adalah untuk menanamkan konsep: (1) menyatakan pecahan ke bentuk lain yang ekuivalen; (2) menyederhanakan pecahan; (3) membandingkan dua pecahan; dan (4) melakukan operasi hitung pecahan. Blok pecahan banyak dipilih oleh sebagian orang sebagai alat peraga matematika khususnya materi pecahan, karena blok pecahan memenuhi syarat alat peraga yang diungkapkan oleh Ruseffendi, (2009:230-231) yaitu ada beberapa persyaratan yang harus dimiliki alat peraga agar fungsi atau manfaat dari alat peraga tersebut sesuai dengan yang diharapkan dalam pembelajaran: (1) sesuai dengan konsep matematika, (2) dapat memperjelas konsep matematika, baik dalam bentuk real (nyata), gambar atau diagram dan bukan sebaliknya mempersulit pemahaman konsep matematika, (3) tahan lama, terbuat dari bahan-bahan yang cukup kuat, (4) bentuk dan warnanya menarik, (5) dari bahan yang aman bagi kesehatan siswa, (6) sederhana dan mudah dikelola, (7) ukurannya sesuai atau seimbang dengan ukuran fisik dari siswa, (8) peragaan diharapkan menjadi dasar bagi tumbuhnya konsep berpikir abstrak, (9) bagi siswa, karena alat peraga tersebut dapat dimanipulasi (dapat 8 diraba, dipegang, dipindahkan, dipasangkan, dan sebagainya) agar siswa dapat belajar secara aktif baik secara individual maupun kelompok, dan (10) bila mungkin alat peraga tersebut dapat bermanfaat banyak. ➢ Kelebihan alat peraga blok pecahan : 1) Dapat memperjelas konsep matematika, dalam bentuk real (nyata); 2) Tahan lama; 3) Bentuk dan warnanya menarik; 4) Dari bahan yang aman bagi kesehatan siswa; 5) Mudah digunakan siswa, karena alat peraga tersebut dapat dipegang, dipindahkan, dipasangkan, dan sebagainya. Sehingga siswa dapat belajar secara aktif baik secara individual maupun kelompok; 6) Alat peraga blok pecahan ini berbentuk lingkaran sehingga cocok digunakan untuk menjelaskan konsep pecahan karena memudahkan guru atau siswa dalam memotong atau membagi lingkaran tersebut menjadi beberapa bagian. Misalnya, siswa membandingkan pecahan dan dengan melihat besarnya potongan dari blok pecahan tersebut pemahaman siswa lebih tepat mana yang lebih besar karena pembelajaran lebih konkrit. ➢ Kekurangan alat peraga blok pecahan : 1) Sulit digunakan ketika angka pembilang lebih besar dari pada penyebut; 2) Sulit digunakan ketika angka penyebutnya sangat besar; 3) Tidak adanya audio sehingga guru harus lebih aktif dalam menjelaskannya 9 BAB III PEMBAHASAN 3.1 Miskonsepsi Siswa Apabila siswa melakukan kesalahan dalam memahami konsep yang seharusnya, maka akibatnya akan menimbulkan miskonsepsi. Berikut ini merupakan hasil wawancara yang dilakukan melalui pemberian soal tentang pemahaman pecahan sederhana terhadap beberapa siswa. Tentukanlah bentuk pecahan bagian yang di arsir dari bagian keseluruhan gambar berikut. Gambar 3.1 Jawaban seorang siswa mengenai soal di atas yaitu 1 5 dengan alasan karena bagian yang diarsi ada satu kotak dan yang tidak di arsir ada 5 kotak 1 sehingga iya menyimpulkan dengan sangat yakin bahwa jawabannya adalah 5. Siswa menganggap bahwa untuk membentuk pecahan dari gambar yang membuat bagian yang di arsir sebagai pembilang dan bagian yang tidak di arsir sebagai penyebut, seharusnya untuk penyebut menggunakan bagian dari keseluruhan gambar Dari jawaban tersebut dapat diketahui bahwa siswa belum betul-betul mengetahui konsep suatu bilangan pecahan. Dimana yang dalam pendapat bennett, et al (2010: 283) yang mengilustrasikan pecahan menjadi 3 konsep yaitu konsep pecahan sebagai bagian dari keseluruhan , konsep pecahan sebagai hasil bagi, dan konsep pecahan sebagai rasio. Siswa belum memahami konsep pecahan sebagai bagian dari keseluruhan yang jika diterjemahkan dalam bentuk 10 penulisan pecahan, pembilang menunjukan jumlah keseluruhan yang dimaksud dan pada penyebut menunjukkan jumlah bagian yang dipertimbangkan. Soal lain yang juga saya berikan kepada siswa adalah “ coba berikan gambar dari bentuk pecahan 3 4 3 dan 7“. Dan berikut gambar jawaban siswa dari soal saya tersebut ( saya menggambarkan dua persegi panjang yang ukurannya sama dan mereka sendiri yang membagi dan mengarsir bagian-bagian pecahan dari soal ) : 3/4 3/6 Gambar 3.2 Dari jawaban siswa pada gambar 3.2 , dapat dilihat bahwa pemahaman siswa mengatakan bahwa konsep pecahan part whole noncongruent part (bagian dari suatu daerah, bagian-bagiannya tidak kongruen) tanpa membentuk gambar tersebut menjadi bagian-bagian yang kongruen. Padahal seharusnya siswa menggambar dengam memerhatikan atau menggunakan konsep pecahan sebagai part whole congruent part (bagian dari suatu daerah, bagian-bagiannya kongruen). Jawaban tersebut mengindikasikan bahwa siswa mengalami salah konsep atau miskonsepsi. Setelah menggambar bagian dari bilangan pecahan (Gambar 3.2), kemudian saya menyakan kepada siswa tersebut “pecahan mana yang nilainya lebih besar?”. Siswa tersebut menjawab bilangan pecahan yang lebih besar adalah 3 6 alasannya karena pada gambar pecahan 3 6 menghasilkan lebih banyak bagian bagian. Namun, jawaban siswa tersebut tentu merupakan miskonsepsi sebab ia menganggap semakin banyak bagian yang terbentuk maka akan semakin besar pula nilai dari pecahannya. Miskonsepsi tersebut disebabkan karena siswa belum memahami bahwa pada konsep perbandingan pecahan yaitu: 11 1. Jika penyebutnya sama: semakin besar pembilang, semakin besar nilai pacahannya. 2. Jika pembilangnya sama: semakin besar penyebut, semakin kecil nilai pecahannya. Jika berpegangan pada konsep tersebut, yang sama sehingga 3 4 3 4 dan 3 6 memiliki pembilang 3 merupakan pecahan yang lebih besar karena 6 memiliki penyebut yang lebih besar . berikut gambar dari masing-masing bilangan pecahan : 1/4 1/4 1/4 3/4 3/6 Gambar 3.3 Pertanyaan berikutnya yang saya tanyakan adalah “apakah bilangan 1/2 dan 3/6 memiliki nilai yang sama ?”. siswa tersebut mengatakan bahwa kedua pecahan tersebut memiliki nilai yang berbeda sebab dilihat dari kedua bilangan pecahan tersebut bahkan tidak ada angka yang sama sehingga nilai keduanya pun pasti berbeda. Miskonsepsi ini menunjukkan bahwa siswa tidak mengetahui konsep pecahan senilai, yaitu Suatu pecahan bisa jadi memiliki bentuk lain, namun tetap sama nilainya. Gambar berikut menunjukkan pecahan yang berbeda namun nilainya sama. 1/2 2/4 3/6 Gambar 3.4 Bagian gambar yang diarsir pada setiap gambar (Gambar 3.4) persegi 1 2 3 memiliki besar yang sama. Jika disimbolkan menjadi 2 = 4 = 6 , maka pecahan tersebut adalah pecahan senilai. Pecahan senilai merupakan pecahan- pecahan 12 yang memiliki nilai sama. Jika sebuah pecahan dikalikan dengan 1, maka nilai pecahan tersebut tidak berubah. Dalam sebuah pecahan, ketika pembilang dan penyebut adalah bilangan yang sama, maka pecahan tersebut nilainya adalah 1 2 ( 2, 3 , 3 4 , dst..). Jadi, pecahan yang dikalikan dengan suatu pecahan yang 4 pembilang dan penyebutnya adalah bilangan yang sama, akan menghasilkan pecahan yang senilai. 1 2 2 1 3 3 Misal : 2 × 2 = 4 atau 2 × 3 = 6 1 2 3 Jadi, 2 = 4 = 6 Pada akhir wawancara saya memberikan 2 soal tentang penjumlahan dan pengurangan pecahan pada siswa lalu meminta untuk menjawabnya. berikut jawaban siswa tersebut. Gambar 3.5 Jawaban siswa seperti disajikan pada gambar 3.5, Siswa menyamakan penyebut pecahan tersebut dengan cara mengali silang. siswa mengalami miskonsepsi karena beranggapan untuk menyamakan penyebut dari pecahan tersebut harus dikali silang. Berdasarkan wawancara yang dilakukan terhadap siswa, siswa mengatakan cara yang digunakan untuk mencari penjumlahan dan pengurangan pecahan tersebut diperoleh dari guru yang mengajarkan pelajaran matematika di kelas, padahal konsep tersebut bukan termasuk konsep ilmiah meskipun pada dasarnya hasilnya benar. Menurut Adinawan, dkk (2007) untuk menyelesaikan penjumlahan dan pengurangan pecahan seharusnya dicari terlebih dahulu KPK dari penyebutnya agar penyebutnya menjadi sama, kemudian dicari pembilang dari pecahan – pecahan tersebut selanjutnya dijumlahkan atau dikurangkan. Sebagaimana dikemukakan oleh Liliawati (2008), terdapat beberapa hal yang dapat menyebabkan terjadinya miskonsepsi, salah satunya adalah metode mengajar dimana miskonsepsi dapat terjadi karena pengungkapan aplikasi yang salah dari konsep yang bersangkutan sehingga mengakibatkan miskonsepsi. Kesalahan 13 yang dilakukan oleh YS juga dialami oleh siswa pada jenjang SMP sebagaimana yang terdapat pada penelitian Maria Endah, dkk (2016) bahwa siswa dalam menyelesaikan penjumlahan dan pengurangan pecahan dengan cara mengali silang penyebut dan pembilang pecahan. 3.2 Alat Peraga Blok Pecahan Alat peraga berasal dari kata “raga” artinya benda yang diraba, dilihat, didengar, dan dapat diamati melalui panca indra kita. Alat peraga adalah segala sesuatu yang dapat memberi rangsangan kepada alat indra sebagai interaksi pembelajaran dapat berjalan dengan baik, pesan yang disampaikan dapat diterima dengan jelas, mudah dimengerti, konkrit, dan tahan lama dalam ingatan siswa. Blok pecahan adalah alat peraga yang berbentuk potongan-potongan yang dibagi beberapa bagian. Alat peraga blok pecahan yang dimaksud penulis disini terbuat dari karton kemudian diberi warna agar menarik perhatian siswa. Alat peraga blok pecahan ini berbentuk lingkaran, kemudian dibagi-bagi berdasarkan 1 1 1 1 1 nilainya. Misalnya 2, 3, 4, 5, 6 dengan setiap bagian besarnya sama Lingkaran utuh seperti yang terlihat pada gambar digunakan untuk memperagakan bilangan 1. Bagian lingkaran yang berwarna kuning sebagai pembilang sedangkan penyebutnya adalah banyaknya bagian yang terbentuk dari blok pecahan tersebut. Terdapat juga lingkaran yang dipotong menjadi 2 bagian sama besar dan 1 bagian berwarna kuning digunakan untuk memperagakan 1 konsep pecahan 2. Lingkaran yang dipotong menjadi 4 bagian sama digunakan 1 untuk memperagakan konsep pecahan 4, bila bagian berwarna kuning ada 2 potong, maka disebut 2 4 (dua per empat) dan bila bagian berwarna kuning ada 3 14 potong, maka disebut 3 4 1 1 (tuga per empat). Peragaan dapat dilanjutkan untuk 5, 6, 1 , dan seterusnya. 7 1. membuktikan pecahan senilai dengan blok pecahan 1 3 Kita akan coba membuktikan bahwa pecahan 2 senilai dengan pecahan 6 . pertama-tama siapkan blok pecahan 1 2 kemudian ambillah bagian yang berwarna kuning pada blok pecahan tersebut. Selanjutnya ambil 3 potong bagian berwarna blok pecahan pada blok pecahan 1 2 1 6 untuk menghasilkan pecahan 3 6 lalu letakkan untuk mengisi bagian yang kosong, maka bagian 3 6 tersebut akan pas mengisi bagian kosong yang sebelumnya ditempati oleh 1 blok pecahan 2 berwarna kuning. Berikut gambar pembuktiannya : 2. Penggunaan blok pecahan untuk perbandingan pecahan Membandingkan bilangan pecahan yang penyebutnya sama, misalnya 1 4 2 dan 4 . seperti pada gambar : Dari alat peraga blok pecahan tersebut dapat diketahui bahwa pecahan lebih besar dari 1 4 2 4 . Hal ini disebabkan oleh luas potongan yang berwarna merah pada pecahan 2 4 lebih besar dari luas potongan yang berwarna merah 1 pada pecahan 4. 15 2 2 Membandingkan pecahan dengan pembilang sama, misalnya 3 dengan 5. Seperti pada gambar : Berdasarkan alat peraga blok pecahan dapat diketahui bahwa pecahan 2 3 2 lebih besar dari 5. Karena luas potongan pecahan berwarna merah pada pecahan 2 3 2 lebih besar dari luas potongan yang berwarna merah pada pecahan 5. 3. Penggunaan alat peraga blok pecahan untuk penjumlahan dan penguranga pecahan berpenyebut sama Penjumlahan pecahan berpenyebut sama dapat dilakukan dengan cara membalikan warna putih menjadi warna kuning sesuai angka pembilang. Karena alat peraga blok pecahan yang dimaksud ini warna kuning sebagai pembilang dan warna hijau sebagai bukan daerah yang 1 1 2 dimaksud . Contoh 4 + 4 = 4 Pengurangan pecahan berpenyebut sama dapat dilakukan dengan cara membalikkan potongan pecahan yang berwarna hijau menjadi warna merah sesuai dengan angka pembilang pada pecahan pertama. Kemudian pada pecahan kedua dengan membalikkan potongan berwarna merah yang 16 telah dibalik tadi sesuai dengan angka pembilang pada pecahan kedua. 3 2 1 Contoh 5 - 5 = 5 17 BAB IV PENUTUP 4.1 Kesimpulan Sangat penting untuk mempelajari dan memahami konsep pecahan karena pecahan juga merupakan dasar dari berbagai macam materi dalam matematika. jika konsep awal yang dipelajari siswa salah atau bahkan tidak mengetahui konsepnya maka untuk penerapan konsep itu pada pengetahuan selanjutnya akan salah juga dan hal tersebut akan menimbulkan berbagai kesalahan. Pecahan menjadi landasan bagi siswa dalam mempelajari matematika selanjutnya seperti persen, rasio, dan aljabar. Pemahaman terhadap konsep bilangan pecahan beserta operasinya dapat dilakukan dengan menggunakan alat peraga blok pecahan . memahami konsep bilangan pecahan menggunakan alat peraga merupakan metode pembelajaran yang menarik dan bermakna serta siswa juga lebih aktif ikut terlibat didalam memahami materi pembelajaran. Siswa dapat memahami operasi logis dari konsep matematika, sehingga ilmu yang disampaikan dapat diserap dengan mudah dan mengingatnya lebih lama. 4.2 Saran pembelajaran yang dilakukan guru untuk mengajarkan konsep pecahan sebaiknya menggunakan alat peraga agar pemahaman konsep dapat lebih mudah diserap oleh siswa , guru juga sebaiknya memberikan penekanan pada setiap konsep serta mengkaitkan konsep satu dengan konsep yang lain. 18 DAFTAR PUSTAKA Rafiah Rahma Pulungan.2019.Analisis Miskonsepsi Siswa Pada Konsep pecahan.sumber: http://repository.upi.edu/35758/3/T_MTK_1706650_Chapter2.pdf http://repo.iain-tulungagung.ac.id/5718/5/Bab%202.pdf Rahmaya Anjelita.2019.Penggunaan Alat Peraga Blok Pecahan Untuk Menngkatkan Pemahaman Konsep Siswa Pada Materi Pecahan Kelas III. Sumber: https://repository.arraniry.ac.id/id/eprint/11185/1/Rahmaya%20Anjelita%2C%20150209063%2C%20FTK %2C%20PGMI%2C%20082167777610.pdf Nurhamdiah.2019.Profil Miskonsepsi Siswa Pada Materi Pecahan Berdasarkan Tingkat Kemampuan Matematika Siswa. Sumber: http://jurnal.umtapsel.ac.id/index.php/eksakta/article/view/684 19 LAMPIRAN Gambar alat peraga Blok Pecahan : 20