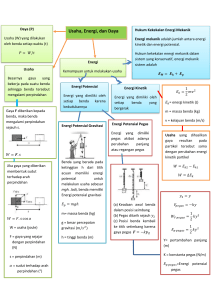
KERJA DAN ENERGI KERJA DAN ENERGI Definisi Kerja atau Usaha : 2 W12 Fdx Newton meter [ Nm] Joule [J] 1 Energi Potensial Gravitasi: • Kerja yang diperlukan untuk membawa benda dari suatu posisi ke posisi lain • Diperlukan gaya F sebesar mg untuk membawa benda dengan kecepatan konstan (percepatan = 0) : y2 = h F h y1 = 0 2 2 2 1 1 1 y y2 W12 Fdy mg dy mg dy mg y y y mg ( y 2 y1 ) 1 y1 0 y 2 h E P mgh mg Energi Kinetik • Energi yang diperlukan untuk mengubah kecepatan benda dari kecepatan awal v1 ke kecepatan akhir v2 v1 = 0 v2 = v F 2 2 2 2 dv dx W12 Fdx ma dx m dx m dv dt dt 1 1 1 1 2 vv2 1 2 1 1 2 W12 m v dv m v mv 2 mv12 2 v v1 2 2 1 1 v1 0 v 2 v E K mv 2 2 Energi Potensial Pegas • Energi yang diperlukan untuk menggerakkan pegas sejauh jarak tertentu (mengubah panjang pegas dari x1 menjadi x2 • Diperlukan gaya F untuk melawan gaya balik Fb x1 = 0 Fb Fb = - k x F = k x F x2 = x k = konstanta pegas x 2 2 2 x x 2 1 2 1 2 1 2 W12 Fdx kx dx k x dx k x kx 2 kx1 2 x x1 2 2 1 1 1 1 2 x1 0 x 2 x E P kx 2 HUKUM KEKEKALAN KERJA DAN ENERGI • Energi akhir benda E2 sama dengan jumlah energi mula-mula E2 dan kerja yang terjadi • Bila benda melakukan kerja, maka kerjanya negatip • Bila kerja dilakukan terhadap benda, maka kerjanya positip E1 W12 E 2 E1 = Energi mula-mula E2 = 1 E1 E K1 E P1 mv12 mgh 1 W12 = 2 1 2 E 2 E K 2 E P 2 mv 2 mgh 2 2 1 1 2 mv1 mgh 1 W12 mv 22 mgh 2 2 2 Energi akhir Kerja 1 2 Contoh Soal 3.1 Seorang mahasiswa menjatuhkan sebuah buku bermassa 2 kg dari ketinggian 10 m. Buku tersebut ditangkap oleh temannya yang berada di tanah. Berapa kecepatannya pada saat ditangkap pada ketinggian 1,5 m ? Jawab : E1 E 2 v1 0 1 1 2 mgh 1 mv1 mgh 2 mv 22 2 2 1 mg (h1 h 2 ) mv 22 2 v 22 2g(h1 h 2 ) v 2(9,8)(10 1,5) 12,9 m s Contoh Soal 3. 2 Sebuah balok bermassa 2,5 kg yang sedang bergerak di atas lantai kasar menumbuk pegas dengan konstanta pegas 320 N/m. Akibatnya balok tersebut berhenti setelah menekan pegas sejauh 7,5 cm. Bila koefisien gesekan antara balok dan lantai kasar adalah 0,25 berapa kecepatan balok pada saat mulai menekan pegas ? Jawab : E1 W12 E 2 E K1 W12 E P 2 W12 f x N x mg x 1 1 1 1 mv12 mg x kx 2 mv12 kx 2 mg x 2 2 2 2 1 1 2 (2,5) v1 (320)(0,075) 2 0,25(2,5)(9,8)(0,075) 2 2 0,9 0,46 m 2 v1 1,088 v1 1,043 1,25 s Contoh Soal 3.3 Tarzan yang beratnya 688 N berayun pada sebuah akar pohon sepanjang 18 m dari suatu puncak bukit. Ia bermaksud menjemput Jane yang berada dibukit lain yang 3,2 m lebih rendah. Bila tegangan maksimum yang mampu ditahan oleh akar pohon adalah 850 N, apakah akan terjadi kecelakaan (akar pohon putus) ? Jawab : Kekekalan Energi : 1 mgh 1 mgh 2 mv 22 2 mv 22 2mg (h1 h 2 ) 2(688)(3,2) 4403,2 E1 E 2 Dinamika gerak melingkar : v 22 4403,2 F ma m R 18 144,2 N F T mg T F mg 144,2 688 832,2 N Karena T< 850 N tidak terjadi kecelakaan Contoh Soal 3.4 Seorang anak yang bermassa 30 kg bermain papan luncur yang panjangnya 5 meter dan membentuk sudut 20o terhadap horisontal. Koefisien gesekan pada papan luncur adalah 0,1. Anak tersebut mulai turun dengan kecepatan awal sebesar 0,8 m/s. Hitung kecepatannya pada saat tiba di tanah. f m = 30 L=5 V1= 0,8 h1 = L sin = 0,1 =20o V2 = ? h2 = 0 Jawab : m = 30 f L=5 V1= 0,8 h1 = L sin = 0,1 =20o V2 = ? h2 = 0 N mg cos f N mg cos (0,1)(30)(9,8)(cos 20o ) 27,6 N E1 W12 E 2 E K1 E P1 W12 E K 2 E P 2 1 1 2 mv1 mgh 1 f L mv 22 0 2 2 1 1 2 o (30)(0,8) (30)(9,8)(5 sin 20 ) 27,6(5) (30) v 22 2 2 v 22 24,958 v 2 24,958 4,996 5 m / s Contoh Soal 3.5 Sebuah balok berada di atas suatu bidang miring yang panjangnya 2 m dan membentuk sudut 30 o terhadap horisontal. Mula-mula balok tersebut dipegang tetap kemudian dilepaskan sehingga ia turun ke bawah. Bila ternyata kecepatannya adalah 2 m/s pada saat tiba di tanah, tentukan koefisien gesekan antara balok dan bidang miring N v1 =0 f mg sin 30o L=2 mg cos 30o mg =30o V2 = 2 h1 = 0 =? h N Jawab : N mg cos 30o V1 =0 f N mg cos 30 f mg sin 30o 2m mg cos 30o mg =? 30o 2 m/s 1 mv 22 2 1 mg (2 sin 30o ) (mg cos 30)2 mv 22 2 1 9,8(1) 9,8(0,866)2 2 2 16,974 9,8 2 7,8 2 7,8 0,566 16,974 E1 W12 E 2 mgh fL h Terima Kasih