Uploaded by
common.user67897
Semiconductor Fundamentals: The Semiconductor in Equilibrium
advertisement

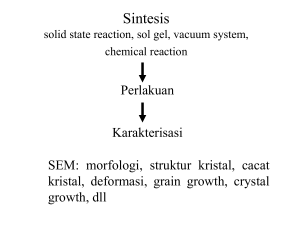
EMT 127 Semiconductor Fundamentals The Semiconductor in Equilibrium Dr. Ala’eddin A. Saif Semester II Academic session 2013/2014 1 Charge carrier in Semiconductors In semiconductor, two types of charge carrier, the electrons (in the conduction band) and the holes (in the valance band). The distribution of electrons in the conduction band is given by (E) = is the density of quantum states in the conduction band The distribution of holes in the valance band is given by = [1 − (E)] is the density of quantum states in the valance band In intrensic semiconductor, no impurities and no lattice defect, EF is located at halfway between Ec and Ev. 2 The thermal-equilibrium electrons concentration (no) is the integration of the n(E) equation over entire conduction-band energy. (E) = E c E F n o N c exp kT ⇒ Nc is the effective density of states function in the conduction band and given as ⁄ ∗ =2 . The thermal-equilibrium holes concentration (po) is the integration of the p(E) equation over entire valance-band energy. = [1 − (E)] ⇒ E F E p o N exp kT Nv is the effective density of states function in the valance band and given by =2 ∗ ⁄ . 3 In intrinsic semiconductor, Intrinsic electron concentration (ni) = Intrinsic hole concentration (pi) In intrinsic semiconductor, Fermi energy level is called the intrinsic Fermi energy, or EF = EFi . Bandgap energy ni is constant for a given semiconductor material at a constant temperature and it is independent of the Fermi energy. 4 Solved Problems 1. Calculate the probability that a quantum state in the conduction band at E = Ec + kT/2 is occupied by an electron, and calculate the thermal equilibrium electron concentration in silicon at T = 300 K. Assume the Fermi energy is 0.25 eV below the conduction band. The value of Nc for silicon at T = 300 K is 2.8 × 1019 cm-3. 2. Calculate the thermal-equilibrium hole concentration in silicon at T = 400 K. Assume that the Fermi energy is 0.27 eV above the valance band energy. The value of Nv at T = 300 K is 1.04 × 1019 cm-3. 3. If Nc and Nv for silicon at T = 300 K are 2.8 × 1019 cm-3 and 1.04 × 1019 cm-3 , respectively. Both Nc and Nv vary as T3/2. Assume the bandgap energy of silicon is 1.12 eV. Calculate the intrinsic carrier concentration in silicon at T = 250 K and T = 400 K. 5 The extrinsic semiconductor Extrinsic semiconductor is defined as a semiconductor in which controlled amounts of specific dopant or impurity atom have been added so that the thermal-equilibrium electron and hole concentrations are different from the intrinsic carrier concentration. n-types semiconductor At very low temperature, the donor (excess) electron is still bound to the phosphorous atom. Intrinsic silicon lattice silicon lattice doped with P atom However, the donor electron is loosely bound to the impurity atom and can become free with small amount of thermal energy. Impurity atom is then ionized and positively charged. 6 Little energy required to move donor electrons from donor states to conduction band, leaving behind a positively charged phosphorous ion. The electrons in the conduction band can move through the crystal freely, while the positively charged ions are fixed in the crystal. The donor impurity atoms add electrons to the conduction band without creating holes in the valance band. 7 p-types semiconductor One covalent bond is incomplete for Si. If an electron were to occupy the empty position, its energy would have to be greater than that of the valance electrons The electron occupying the empty position does not have sufficient energy to be in the conduction band. With little thermal energy, a valence electron can break from another covalent bond and can occupy this position, thus creating a hole at the location of the broken covalent bond. The acceptor impurity is then ionized and negatively charged. little energy required to move valence electrons to acceptor levels. negatively charged acceptor ions are fixed but holes in the valence band can move through the crystal. The acceptor impurity atom can generate holes in the valance band without generating electrons in the conduction band. p-types semiconductor n-types semiconductor Majority carrier electrons Minority carrier electrons EF < EFi no < po EF > EFi no > po Minority carrier holes Majority carrier holes E c E F n o N c exp kT by adding and subtracting EFi but Then Using the same technique n-type semiconductor, EF > EFi , no > ni, po < ni → no > po p-type semiconductor, EF < EFi , no < ni, po > ni → no < po Statistics of donors and acceptors Probability function of electrons occupying the donor state is Nd nd 1 E E F 1 exp d 2 kT N a is the concentration of donor atoms. nd is the concentration of electrons in the donor level. Ed is the energy of the donor level. nd can be written as nd N d N d N d Is the concentration of ionized donors. Probability function of holes occupying the acceptor state is Na pa N a N a 1 E Ea 1 exp F 2 kT N a is the concentration of acceptor atoms. pa is the concentration of holes in the acceptor level. Ed is the acceptor energy level. N a Is the concentration of ionized acceptors. Statistics of donors and acceptors 14 Complete Ionization and Freeze -Out nd Nd 1 E E F 1 exp d 2 kT Density of negative charges = density of positive charges Position of Fermi energy level Solved Problems 4. consider silicon at T = 300 K so that Nc = 2.8 × 1019 cm-3. and Nv = 1.04 × 1019 cm-3. assume that the Fermi energy is 0.25 eV below the conduction band. If we assume that the bandgap energy of silicon is 1.12 eV, then Fermi energy will be 0.87 eV above the valance band. Determine the thermal equilibrium concentration of electrons and holes. 5. Consider phosphorous doping in silicon, for T 300 K, at a concentration of Nd = 1016 cm-3. Determine the fraction of total electrons still in the donor state. Nc = 2.8 × 1019 cm-3 5. Determine the thermal-equilibrium electron and hole concentrations in silicon at T = 300 K for given doping concentration. (a) Nd = 1016 cm-3 and Na = 0. (b) Nd = 5 × 1015 cm-3 and Na = 2 × 1015 cm-3. ni = 1.5 × 1010 cm-3 29 Assignment 1. The lattice constant of a simple cubic lattice is ao. Thus, (a) Sketch the following planes: (i) (220) and (ii) (321). (b) Sketch the following directions: (i) [220] and (ii) [321]. 2. For the silicon unit cell. (a) Determine the number of corner atoms, (b) Determine number of face-center atom, (c) Determine number of atoms totally enclosed in the unit cell and (d) if the lattice constant is 5.43 Å calculate the volume density of silicon atom. 3. If the average energy of an electron at thermal equilibrium is 3kT/2. Determine its (a) energy in eV, (b) average electron momentum and (c) the de Broglie wavelength. 4. Determine the probability that an energy level is (a) occupied by an electron if it is above Fermi level by 4kT and (b) empty of an electron if it is below Fermi level by 4kT. What is your conclusion? 5. The probability that a state at Ec + kT is occupied by an electron is equal to the probability that a state at Ev – kT is empty. Determine the position of the Fermi level as a function of Ec and Ev. 6. The Fermi energy level for a particular material at T = 300 K is 5.5 eV. The electrons in this material follow the Fermi-Dirac distribution function. (a) Find the probability of an electron occupying an energy state of 5.8 eV. (b) If the temperature increased to T = 700 K, repeat part (a). Assume E F is constant. (c) Determine the temperature at which there is 2% probability that a state of 0.25 eV below Fermi level will be empty of an electron. 30 7. Determine the thermal equilibrium concentration of electrons and holes in silicon at T = 300 K so that Nc = 2.8 × 1019 cm-3. and Nv = 1.04 × 1019 cm-3 for the case that the Fermi level is 0.22 eV below the conduction band energy Ec. Consider the band gap energy Eg is 1.12 eV. 8. Consider phosphorous doping in silicon, for T = 300 K, at a concentration of Nd = 1016 cm-3. Determine the fraction of total electrons still in the donor state. Consider Nc = 2.8 × 1019 cm-3 and the ionization energy for the donor electrons is 0.045 eV. Recalculate the value of the fraction at T = 200 K. 9. Consider silicon at T = 300 K with doping concentration of Nd = 8 × 1015 cm-3 and Na = 5 × 1015 cm-3 Determine the position of Fermi energy level with respect to Ec. Consider Nc = 2.8 × 1019 cm-3.