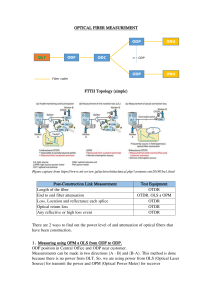
Uploaded by
common.user56038
OptiSystem Component Library: Optical Communication Design Software
advertisement

OptiSystem Component Library Optical Communication System Design Software Version 7.0 for Windows® XP/Vista OptiSystem Component Library Optical Communication System Design Software Copyright © 2008 Optiwave All rights reserved. All OptiSystem documents, including this one, and the information contained therein, is copyright material. No part of this document may be reproduced, stored in a retrieval system, or transmitted in any form or by any means whatsoever, including recording, photocopying, or faxing, without prior written approval of Optiwave. Disclaimer Optiwave makes no representation or warranty with respect to the adequacy of this documentation or the programs which it describes for any particular purpose or with respect to its adequacy to produce any particular result. In no event shall Optiwave, its employees, its contractors or the authors of this documentation, be liable for special, direct, indirect, or consequential damages, losses, costs, charges, claims, demands, or claim for lost profits, fees, or expenses of any nature or kind. Technical support If you purchased Optiwave software from a distributor that is not listed here, please send technical questions to your distributor. Optiwave Canada/US Tel (613) 224-4700 E-mail [email protected] Fax (613) 224-4706 URL www.optiwave.com Cybernet Systems Co., Ltd. Japan Tel +81 (03) 5978-5414 E-mail [email protected] Fax +81 (03) 5978-6082 URL www.cybernet.co.jp Optiwave Europe Europe Tel +33 (0) 494 08 27 97 E-mail [email protected] Fax +33 (0) 494 33 65 76 URL www.optiwave.eu Table of contents Transmitters Library ........................................................................................ 1 Pulse Generators ...................................................................................................... 5 Electrical ..............................................................................................................................5 Duobinary Pulse Generator........................................................................................5 Electrical Jitter............................................................................................................7 Noise Source..............................................................................................................9 RZ Pulse Generator .................................................................................................11 NRZ Pulse Generator...............................................................................................15 Gaussian Pulse Generator .......................................................................................19 Hyperbolic-Secant Pulse Generator.........................................................................21 Sine Generator.........................................................................................................23 Triangle Pulse Generator .........................................................................................25 Saw-Up Pulse Generator .........................................................................................27 Saw-Down Pulse Generator.....................................................................................29 Impulse Generator ...................................................................................................31 Raised Cosine Pulse Generator...............................................................................33 Sine Pulse Generator...............................................................................................35 Measured Pulse .......................................................................................................37 Measured Pulse Sequence ......................................................................................39 Bias Generator .........................................................................................................41 M-Ary Pulse Generator ............................................................................................43 M-ary Raised Cosine Pulse Generator ....................................................................45 Predistortion .............................................................................................................47 Optical................................................................................................................................49 Optical Gaussian Pulse Generator...........................................................................49 Optical Sech Pulse Generator..................................................................................53 Optical Impulse Generator .......................................................................................57 Measured Optical Pulse ...........................................................................................61 Measured Optical Pulse Sequence..........................................................................65 Time Resolve Chirp (TRC) Measurement Data .......................................................69 Spatial Optical Gaussian Pulse Generator...............................................................73 Spatial Optical Sech Pulse Generator......................................................................77 Spatial Optical Impulse Generator ...........................................................................81 Optical Sources....................................................................................................... 85 CW Laser .................................................................................................................85 Laser Rate Equations...............................................................................................89 Laser Measured .......................................................................................................95 LED ........................................................................................................................103 White Light Source.................................................................................................105 Pump Laser............................................................................................................107 Pump Laser Array ..................................................................................................109 Controlled Pump Laser ..........................................................................................113 CW Laser Array......................................................................................................115 CW Laser Array ES................................................................................................119 CW Laser Measured ..............................................................................................123 Directly Modulated Laser Measured ......................................................................129 VCSEL Laser .........................................................................................................137 Spatial CW Laser ...................................................................................................149 Spatiotemporal VCSEL ..........................................................................................153 Spatial VCSEL .......................................................................................................161 Spatial Laser Rate Equations.................................................................................169 Spatial LED ............................................................................................................173 Optical Transmitters ............................................................................................. 177 WDM Transmitter ...................................................................................................177 Optical Transmitter.................................................................................................185 Spatial Optical Transmitter .....................................................................................191 Bit Sequence Generators ..................................................................................... 195 Pseudo-Random Bit Sequence Generator.............................................................197 User-Defined Bit Sequence Generator ..................................................................201 Modulators ............................................................................................................. 203 Optical..............................................................................................................................203 Mach-Zehnder Modulator.......................................................................................203 Electroabsorption Modulator ..................................................................................207 Amplitude Modulator ..............................................................................................209 Phase Modulator ....................................................................................................211 Frequency Modulator .............................................................................................213 Dual Drive Mach-Zehnder Modulator Measured ....................................................215 Electroabsorption Modulator Measured .................................................................219 Single Drive Mach-Zehnder Modulator Measured .................................................223 Dual Port Dual Drive Mach-Zehnder Modulator Measured ....................................227 Lithium Niobate Mach-Zehnder Modulator.............................................................231 Multimode Library ................................................................................................. 237 Donut Transverse Mode Generator .......................................................................237 Hermite Transverse Mode Generator ....................................................................241 Laguerre Transverse Mode Generator...................................................................245 Multimode Generator .............................................................................................249 Measured Transverse Mode ..................................................................................253 Optical Fibers Library.................................................................................. 257 Optical fiber ............................................................................................................259 Optical fiber CWDM ...............................................................................................297 Bidirectional Optical Fiber ......................................................................................321 Linear Multimode Fiber ..........................................................................................359 Parabolic-Index Multimode Fiber ...........................................................................365 Measured-Index Multimode Fiber ..........................................................................373 Free Space Optics Library .......................................................................... 383 FSO Channel .........................................................................................................385 OWC Channel ........................................................................................................389 Receivers Library......................................................................................... 393 Multimode ............................................................................................ 395 Mode Combiner......................................................................................................395 Mode Selector ........................................................................................................397 Regenerators ......................................................................................................... 399 Clock Recovery ......................................................................................................399 Data Recovery .......................................................................................................401 3R Regenerator......................................................................................................403 Electronic Equalizer ...............................................................................................407 MLSE Equalizer .....................................................................................................413 Integrate And Dump ...............................................................................................417 Demodulators ........................................................................................................ 419 Ideal Frequency Demodulator................................................................................419 Ideal Phase Demodulator.......................................................................................421 Optical Receivers .................................................................................................. 423 Optical Receiver.....................................................................................................423 Spatial Optical Receiver.........................................................................................427 Photodetectors ...................................................................................................... 431 Photodetector PIN..................................................................................................431 Photodetector APD ................................................................................................437 Spatial PIN Photodetector......................................................................................443 Spatial APD Photodetector ....................................................................................447 Amplifiers Library ........................................................................................ 451 Optical .................................................................................................................... 469 Raman ..............................................................................................................................469 Raman Amplifier—Average Power Model..............................................................469 Raman Amplifier—Dynamic Model ........................................................................479 EDFA ................................................................................................................................489 EDFA Black Box.....................................................................................................489 EDF Dynamic-Full Model .......................................................................................501 EDF Dynamic—Analytical Model ...........................................................................509 EDFA......................................................................................................................517 Optical Amplifier ....................................................................................................525 EDFA Measured.....................................................................................................531 Erbium Doped Fiber ...............................................................................................537 Er-Yb Codoped Fiber .............................................................................................575 Er-Yb Codoped Fiber Dynamic ..............................................................................589 Er-Yb Codoped Waveguide Amplifier ....................................................................599 Yb-Doped Fiber......................................................................................................619 Yb-Doped Fiber Dynamic.......................................................................................633 SOA ..................................................................................................................................643 Traveling Wave SOA .............................................................................................643 Wideband Traveling Wave SOA ............................................................................649 Reflective SOA.......................................................................................................657 Electrical ................................................................................................................ 663 Limiting Amplifier....................................................................................................663 Electrical Amplifier..................................................................................................665 Transimpedance Amplifier .....................................................................................667 AGC Amplifier ........................................................................................................669 Filters Library ............................................................................................... 671 Optical .................................................................................................................... 673 Optical IIR filter.......................................................................................................673 Measured Optical filter ...........................................................................................677 Measured Group Delay Optical filter ......................................................................681 Rectangle Optical filter ...........................................................................................687 Trapezoidal Optical filter ........................................................................................689 Gaussian Optical filter ............................................................................................691 Butterworth Optical filter.........................................................................................693 Bessel Optical filter ................................................................................................695 Fabry Perot Optical filter ........................................................................................699 Acousto Optical filter ..............................................................................................701 Mach-Zehnder Interferometer ................................................................................705 Inverted Optical IIR filter.........................................................................................707 Inverted Rectangle Optical filter .............................................................................711 Inverted Trapezoidal Optical filter ..........................................................................713 Inverted Gaussian Optical filter ..............................................................................715 Inverted Butterworth Optical filter...........................................................................717 Inverted Bessel Optical filter ..................................................................................719 Gain Flattening Filter..............................................................................................721 Delay Interferometer ..............................................................................................725 Transmission Filter Bidirectional ............................................................................727 Reflective Filter Bidirectional..................................................................................731 3-Port Filter Bidirectional........................................................................................735 Periodic Optical Filter .............................................................................................739 FBG ..................................................................................................................................743 Fiber Bragg Grating (FBG) .....................................................................................743 Uniform Fiber Bragg Grating ..................................................................................749 Ideal Dispersion Compensation FBG.....................................................................751 Electrical ................................................................................................................ 757 Low Pass IIR filter ..................................................................................................757 Low Pass Rectangle filter.......................................................................................761 Low Pass Gaussian filter........................................................................................763 Low Pass Butterworth filter ....................................................................................765 Low Pass Bessel filter ............................................................................................767 Low Pass Chebyshev filter .....................................................................................771 Low Pass RC filter..................................................................................................773 Low Pass Raised Cosine filter ...............................................................................775 Low Pass Cosine Roll Off filter...............................................................................777 Low Pass Squared Cosine Roll Off filter ................................................................779 Measured filter .......................................................................................................785 Band Pass Rectangle filter .....................................................................................789 Band Pass Gaussian filter......................................................................................791 Band Pass Butterworth filter...................................................................................793 Band Pass Bessel filter ..........................................................................................795 Band Pass Chebyshev filter ...................................................................................799 Band Pass RC filter................................................................................................801 Band Pass Raised Cosine filter..............................................................................803 Band Pass Cosine Roll Off filter.............................................................................805 Band Pass Square Cosine Roll Off filter ................................................................807 S Parameters Measured filter ................................................................................809 WDM Multiplexers Library........................................................................... 813 Add and Drop ........................................................................................................ 815 WDM Add...............................................................................................................815 WDM Drop .............................................................................................................819 WDM Add and Drop ...............................................................................................823 Demultiplexers ...................................................................................................... 827 WDM Demux 1x2 ...................................................................................................827 WDM Demux 1x4 ...................................................................................................831 WDM Demux 1x8 ...................................................................................................835 WDM Demux..........................................................................................................839 WDM Demux ES ....................................................................................................843 WDM Interleaver Demux........................................................................................845 Ideal Demux ...........................................................................................................847 Multiplexers ........................................................................................................... 849 WDM Mux 2x1........................................................................................................849 WDM Mux 4x1........................................................................................................853 WDM Mux 8x1........................................................................................................857 WDM Mux ..............................................................................................................861 WDM Mux ES.........................................................................................................865 Ideal Mux................................................................................................................867 Nx1 Mux Bidirectional ............................................................................................869 AWG ....................................................................................................................... 873 AWG NxN...............................................................................................................873 AWG NxN Bidirectional ..........................................................................................875 Network Library............................................................................................ 881 Optical Switches ................................................................................................... 883 Dynamic Y Select Nx1 Measured ..........................................................................883 Dynamic Y Switch 1xN Measured..........................................................................887 Dynamic Y Switch 1xN...........................................................................................891 Dynamic Y Select Nx1 ...........................................................................................895 Dynamic Space Switch Matrix NxM Measured ......................................................899 Dynamic Space Switch Matrix NxM .......................................................................903 Optical Switch ........................................................................................................907 Digital Optical Switch .............................................................................................909 Optical Y Switch .....................................................................................................911 Optical Y Select......................................................................................................913 Ideal Switch 2x2 .....................................................................................................915 Ideal Y Switch ........................................................................................................917 Ideal Y Select .........................................................................................................919 Ideal Y Switch 1x4..................................................................................................921 Ideal Y Select 4x1 ..................................................................................................923 Ideal Y Switch 1x8..................................................................................................925 Ideal Y Select 8x1 ..................................................................................................927 Ideal Y Select Nx1..................................................................................................929 Ideal Y Switch 1xN .................................................................................................931 2x2 Switch Bidirectional .........................................................................................933 Frequency Conversion ......................................................................................... 935 Ideal Frequency Converter.....................................................................................935 Passives Library .......................................................................................... 937 Electrical ................................................................................................................ 941 Electrical Phase Shift .............................................................................................941 Electrical Signal Time Delay ..................................................................................943 Attenuators......................................................................................................................945 Electrical Attenuator ...............................................................................................945 Couplers ..........................................................................................................................947 90 Degree Hybrid Coupler .....................................................................................947 180 Degree Hybrid Coupler ...................................................................................949 DC Blockers.....................................................................................................................951 DC Block ................................................................................................................951 Splitters............................................................................................................................953 Splitter 1x2 .............................................................................................................953 Splitter 1xN.............................................................................................................955 Combiners .......................................................................................................................957 Combiner 2x1.........................................................................................................957 Combiner Nx1 ........................................................................................................959 Measured Components ..................................................................................................961 1 Port S Parameters...............................................................................................961 2 Port S Parameters...............................................................................................963 3 Port S Parameters...............................................................................................967 4 Port S Parameters...............................................................................................969 Optical .................................................................................................................... 971 Phase Shift.............................................................................................................971 Time Delay .............................................................................................................973 Attenuators......................................................................................................................975 Optical Attenuator ..................................................................................................975 Attenuator Bidirectional ..........................................................................................977 Connectors ......................................................................................................................981 Connector...............................................................................................................981 Connector Bidirectional ..........................................................................................983 Spatial Connector...................................................................................................987 Reflectors ........................................................................................................................991 Reflector Bidirectional ............................................................................................991 Taps..................................................................................................................................995 Tap Bidirectional ....................................................................................................995 Measured Components ..................................................................................................999 Luna Technologies OVA Measurement .................................................................999 Measured Component..........................................................................................1003 Multimode ......................................................................................................................1007 Spatial Aperture ...................................................................................................1007 Thin Lens .............................................................................................................1009 Vortex Lens ..........................................................................................................1011 Couplers ........................................................................................................................1013 X Coupler .............................................................................................................1013 Pump Coupler Co-Propagating ............................................................................1015 Pump Coupler Counter-Propagating....................................................................1017 Coupler Bidirectional ............................................................................................1019 Pump Coupler Bidirectional..................................................................................1023 Power Splitters..............................................................................................................1023 Power Splitter 1x2 ................................................................................................1029 Power Splitter 1x4 ................................................................................................1031 Power Splitter 1x8 ................................................................................................1033 Power Splitter.......................................................................................................1035 1xN Splitter Bidirectional ......................................................................................1037 Power Combiners .........................................................................................................1041 Power Combiner 2x1............................................................................................1041 Power Combiner 4x1............................................................................................1043 Power Combiner 8x1............................................................................................1045 Power Combiner ..................................................................................................1047 Polarization....................................................................................................................1049 Linear Polarizer ....................................................................................................1049 Circular Polarizer..................................................................................................1051 Polarization Attenuator.........................................................................................1053 Polarization Delay ................................................................................................1055 Polarization Phase Shift .......................................................................................1057 Polarization Combiner..........................................................................................1059 Polarization Controller..........................................................................................1061 Polarization Rotator..............................................................................................1063 Polarization Splitter ..............................................................................................1065 PMD Emulator......................................................................................................1067 Polarization Combiner Bidirectional .....................................................................1071 Polarization Waveplate ........................................................................................1075 Isolators .........................................................................................................................1077 Isolator .................................................................................................................1077 Ideal Isolator.........................................................................................................1079 Isolator Bidirectional.............................................................................................1081 Circulators .....................................................................................................................1085 Circulator..............................................................................................................1085 Ideal Circulator .....................................................................................................1087 Circulator Bidirectional .........................................................................................1089 Signal Processing Library......................................................................... 1093 Arithmetic ............................................................................................................ 1097 Electrical ........................................................................................................................1097 Electrical Gain ......................................................................................................1097 Electrical Adder ....................................................................................................1099 Electrical Subtractor .............................................................................................1101 Electrical Multiplier ...............................................................................................1103 Electrical Bias.......................................................................................................1105 Electrical Norm.....................................................................................................1107 Electrical Differentiator .........................................................................................1109 Electrical Integrator ..............................................................................................1111 Electrical Rescale.................................................................................................1113 Electrical Reciprocal.............................................................................................1115 Electrical Abs .......................................................................................................1117 Electrical Sgn .......................................................................................................1119 Optical............................................................................................................................1083 Optical Gain .........................................................................................................1121 Optical Adder .......................................................................................................1123 Optical Subtractor ................................................................................................1125 Optical Bias ..........................................................................................................1127 Optical Multiplier...................................................................................................1129 Optical Hard Limiter .............................................................................................1131 Tools..................................................................................................................... 1133 Electrical ........................................................................................................................1133 Convert To Electrical Individual Samples.............................................................1133 Convert From Electrical Individual Samples ........................................................1135 Optical............................................................................................................................1137 Merge Optical Signal Bands.................................................................................1137 Convert to Parameterized ....................................................................................1139 Convert to Noise Bins ..........................................................................................1141 Convert To Optical Individual Samples ................................................................1143 Convert From Optical Individual Samples............................................................1145 Optical Downsampler ...........................................................................................1147 Signal Type Selector ............................................................................................1149 Convert To Sampled Signals ...............................................................................1151 Channel Attacher .................................................................................................1153 Logic..................................................................................................................... 1155 Binary.............................................................................................................................1155 Binary NOT ..........................................................................................................1155 Binary AND ..........................................................................................................1157 Binary OR.............................................................................................................1159 Binary XOR ..........................................................................................................1161 Binary NAND........................................................................................................1163 Binary NOR ..........................................................................................................1165 Binary XNOR........................................................................................................1167 Delay ....................................................................................................................1169 Duobinary Precoder .............................................................................................1171 4-DPSK Precoder.................................................................................................1173 Electrical ........................................................................................................................1175 Electrical NOT ......................................................................................................1175 Electrical AND ......................................................................................................1177 Electrical OR ........................................................................................................1179 Electrical XOR......................................................................................................1181 Electrical NAND ...................................................................................................1183 Electrical NOR......................................................................................................1185 Electrical XNOR ...................................................................................................1187 Tools Library .............................................................................................. 1189 Switch...................................................................................................................1191 Select ...................................................................................................................1193 Fork 1x2 ...............................................................................................................1195 Loop Control.........................................................................................................1197 Ground .................................................................................................................1199 Buffer Selector .....................................................................................................1201 Fork 1xN...............................................................................................................1203 Binary Null............................................................................................................1205 Optical Null...........................................................................................................1207 Electrical Null .......................................................................................................1209 Binary Delay.........................................................................................................1211 Optical Delay........................................................................................................1213 Electrical Delay ....................................................................................................1215 Optical Ring Controller .........................................................................................1217 Electrical Ring Controller......................................................................................1219 Duplicator .............................................................................................................1221 Limiter ..................................................................................................................1223 Initializer ...............................................................................................................1225 Save to file ...........................................................................................................1227 Load from file .......................................................................................................1229 Command Line Application ..................................................................................1231 Swap Horiz...........................................................................................................1235 Optiwave Software Tools .......................................................................... 1237 OptiAmplifier.........................................................................................................1239 OptiGrating...........................................................................................................1247 WDM_Phasar Demux 1xN ...................................................................................1251 WDM_Phasar Mux Nx1........................................................................................1253 OptiBPM Component NxM...................................................................................1257 Save Transverse Mode ........................................................................................1261 MATLAB Library......................................................................................... 1265 MATLAB Filter Component ..................................................................................1267 MATLAB Optical Filter Component ......................................................................1271 MATLAB Component ...........................................................................................1275 EDA Cosimulation Library ........................................................................ 1291 Save ADS File......................................................................................................1293 Load ADS File ......................................................................................................1297 Save Spice Stimulus File .....................................................................................1301 Load Spice CSDF File..........................................................................................1307 Triggered Save Spice Stimulus File .....................................................................1311 Triggered Load Spice CSDF File .........................................................................1315 Cable Access Library ................................................................................ 1319 Carrier generators............................................................................................... 1321 Carrier Generator .................................................................................................1321 Carrier Generator Measured ................................................................................1325 Transmitters ........................................................................................................ 1327 Modulators.....................................................................................................................1327 Electrical Amplitude Modulator (AM) ....................................................................1327 Electrical Frequency Modulator (FM) ...................................................................1329 Electrical Phase Modulator (PM)..........................................................................1331 Quadrature Modulator ..........................................................................................1333 PAM Modulator ....................................................................................................1335 QAM Modulator ....................................................................................................1337 PSK Modulator .....................................................................................................1339 DPSK Modulator ..................................................................................................1341 OQPSK Modulator ...............................................................................................1343 MSK Modulator ....................................................................................................1345 FSK Modulator .....................................................................................................1347 CPFSK Modulator ................................................................................................1349 Pulse generators...........................................................................................................1351 PAM Pulse Generator ..........................................................................................1351 QAM Pulse Generator..........................................................................................1353 PSK Pulse Generator...........................................................................................1357 DPSK Pulse Generator ........................................................................................1359 OQPSK Pulse Generator .....................................................................................1361 MSK Pulse Generator ..........................................................................................1363 Sequence generators ...................................................................................................1367 PAM Sequence Generator ...................................................................................1367 QAM Sequence Generator...................................................................................1371 PSK Sequence Generator....................................................................................1375 DPSK Sequence Generator .................................................................................1379 Receivers ............................................................................................................. 1383 Demodulators................................................................................................................1383 Electrical Amplitude Demodulator ........................................................................1383 Electrical Phase Demodulator..............................................................................1385 Electrical Frequency Demodulator .......................................................................1387 Quadrature Demodulator .....................................................................................1389 Decoders........................................................................................................................1391 PAM Sequence Decoder......................................................................................1391 QAM Sequence Decoder .....................................................................................1395 PSK Sequence Decoder ......................................................................................1399 DPSK Sequence Decoder....................................................................................1403 Detectors .......................................................................................................................1407 M-Ary Threshold Detector ....................................................................................1407 Visualizer Library ....................................................................................... 1409 Optical .................................................................................................................. 1411 Optical Spectrum Analyzer (OSA)........................................................................1411 Optical Time Domain Visualizer (OTDV)..............................................................1417 Optical Power Meter.............................................................................................1427 Polarization Meter ................................................................................................1431 Polarization Analyzer ...........................................................................................1437 WDM Analyzer (WDMA) ......................................................................................1445 Dual Port WDM Analyzer (DPWDMA) .................................................................1451 Differential Mode Delay Analyzer.........................................................................1459 Spatial Visualizer..................................................................................................1463 Test Set ..........................................................................................................................1471 Encircled Flux Analyzer........................................................................................1471 Optical Filter Analyzer ..........................................................................................1475 Photonic All-parameter Analyzer..........................................................................1479 Electrical .............................................................................................................. 1483 Oscilloscope Visualizer ........................................................................................1483 RF Spectrum Analyzer (RFSA) ...........................................................................1489 Eye Diagram Analyzer .........................................................................................1495 BER Analyzer.......................................................................................................1513 Electrical Power Meter .........................................................................................1531 Electrical Carrier Analyzer (ECAN) ......................................................................1535 Electrical Constellation Visualizer ........................................................................1541 Test Set ..........................................................................................................................1549 Electrical Filter Analyzer.......................................................................................1549 S Parameter Extractor..........................................................................................1551 Transmitters Library This section contains information on the following transmitters. Pulse Generators Electrical • Duobinary Pulse Generator • Electrical Jitter • Noise Source • RZ Pulse Generator • NRZ Pulse Generator • Gaussian Pulse Generator • Hyperbolic-Secant Pulse Generator • Sine Generator • Triangle Pulse Generator • Saw-Up Pulse Generator • Saw-Down Pulse Generator • Impulse Generator • Raised Cosine Pulse Generator • Sine Pulse Generator • Measured Pulse • Measured Pulse Sequence • Bias Generator • M-Ary Pulse Generator • M-ary Raised Cosine Pulse Generator • Predistortion 1 Optical • Optical Gaussian Pulse Generator • Optical Sech Pulse Generator • Optical Impulse Generator • Measured Optical Pulse • Measured Optical Pulse Sequence • Time Resolve Chirp (TRC) Measurement Data • Spatial Optical Gaussian Pulse Generator • Spatial Optical Sech Pulse Generator • Spatial Optical Impulse Generator Optical Sources • CW Laser • Laser Rate Equations • Laser Measured • LED • White Light Source • Pump Laser • Pump Laser Array • Controlled Pump Laser • CW Laser Array • CW Laser Array ES • CW Laser Measured • Directly Modulated Laser Measured • VCSEL Laser • Spatiotemporal VCSEL • Spatial CW Laser • Spatial VCSEL • Spatial Laser Rate Equations • Spatial LED Optical Transmitters • WDM Transmitter • Optical Transmitter • Spatial Optical Transmitter Bit Sequence Generators • Pseudo-Random Bit Sequence Generator • User-Defined Bit Sequence Generator Modulators Optical • Mach-Zehnder Modulator • Electroabsorption Modulator • Amplitude Modulator • Phase Modulator • Frequency Modulator • Dual Drive Mach-Zehnder Modulator Measured • Electroabsorption Modulator Measured • Single Drive Mach-Zehnder Modulator Measured • Dual Port Dual Drive Mach-Zehnder Modulator Measured • Lithium Niobate Mach-Zehnder Modulator TRANSMITTERS LIBRARY Notes: 4 Duobinary Pulse Generator Used for duobinary modulation schemes. It is equivalent to a subsystem based on an electrical delay and adder. It can be used together with any electrical pulse generator. Ports Name and description Port type Signal type Input Input Electrical Clock Input Binary Output Output Electrical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled DUOBINARY PULSE GENERATOR Technical background The equivalent subsystem is: Figure 1 Duobinary Pulse Generator subsystem 6 ELECTRICAL JITTER Electrical Jitter Inserts jitter in the input signal. Ports Name and description Port type Signal type Input Input Electrical Clock Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 100 MHz Hz, MHz, GHz, THz [0,+INF[ 0.1 UI — [0,+INF[ Name and description Default value Units Value range Enabled True — True, False Jitter frequency Jitter amplitude Jitter amplitude range Simulation Determines whether or not the component is enabled 7 ELECTRICAL JITTER Technical background The jitter is a short-term, non-cumulative variation of the significant instants of a digital signal from their positions in time. Jitter amplitude is measured in unit intervals (UI), where 1 UI is the phase deviation of one clock period. The peak-to-peak UI deviation of the phase function with respect to time is referred as jitter amplitude. The output signal is: A- sin ( 2πft )⎞ E out ( t ) = Ein ⎛ t + -----⎝ 2B ⎠ where A is the jitter amplitude, B is the bit rate, and f is the jitter frequency. 8 NOISE SOURCE Noise Source Source of thermal noise. Ports Name and description Port type Signal type Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range PSD True — — True, False –60 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether the power is defined as PSD or as the average power in time Noise Power Value of the PSD or the average power Simulation Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window 9 NOISE SOURCE Noise Name and description Default value Units Value range Add noise to signal False — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0, 4999] Determines whether the noise will propagate separately from the signal or will be added to the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The average output Power or Power spectral density are parameters that you specify. This model generates electrical sampled signals or electrical sampled noise according to: E out = [ x ( t ) + jy ( t ) ] P ⁄ 2 A Gaussian distribution describes the probability density function for the real and imaginary part of E. P is the average power when PSD parameter is false, if PSD is true then P is calculated from the power spectral density multiplied by the Sample rate. 10 RZ PULSE GENERATOR RZ Pulse Generator Generates a Return to Zero (RZ) coded signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Rectangle shape Exponential — Exponential, Gaussian, Linear, Sine 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Rise time 0.05 bit [0,1] 0.05 bit [0,1] Determines the shape for the edges of the pulse Amplitude Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Duty cycle Duration of the high level bit Defined as the time from when the rising edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Fall time Defined as the time from when the falling edge reaches 90% of the amplitude to the time it reaches 10% of the amplitude 11 RZ PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background According to the parameter Rectangle shape, this model can produce pulses with different edge shapes: Exponential –( t ⁄ cr ) ⎧ ,0 ≤ t < t 1 ⎪1 – e ⎪ 1, t 1 ≤ t < t 2 ⎪ E(t) = ⎨ ⎪ e –( t ⁄ cf ) ,t ≤ t < t 2 c ⎪ ⎪ 0, t c ≤ t < T ⎩ Gaussian 2 –( t ⁄ cr ) ⎧ 1 e – ,0 ≤ t < t 1 ⎪ ⎪ 1, t 1 ≤ t < t 2 ⎪ E(t) = ⎨ 2 ⎪ –( t ⁄ cf ) e ,t 2 ≤ t < t c ⎪ ⎪ 0, t c ≤ t < T ⎩ 12 RZ PULSE GENERATOR Linear ⎧ t ⁄ c r ,0 ≤ t < t 1 ⎪ ⎪ 1, t 1 ≤ t < t 2 E(t) = ⎨ ⎪ t ⁄ cf ,t 2 ≤ t < t c ⎪ ⎩ 0, t c ≤ t < T Sine ⎧ sin ( π.t ⁄ c r ) ,0 ≤ t < t 1 ⎪ 1 ,t 1 ≤ t < t 2 ⎪ E(t) = ⎨ ⎪ sin ( π.t ⁄ c f ) ,t 2 ≤ t < t c ⎪ 0 ,t c ≤ t < T ⎩ where cr is the rise time coefficient and cf is the fall time coefficient. t1 and t2, together with cr and cf, are numerically determinate to generate pulses with the exact values of the parameters Rise time and Fall time. tc is the duty cycle duration, and T is the bit period. 13 RZ PULSE GENERATOR Notes: 14 NRZ PULSE GENERATOR NRZ Pulse Generator Generates a Non Return to Zero (NRZ) coded signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Rectangle shape Exponential — Exponential, Gaussian, Linear, Sine 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ Position 0 bit Rise time 0.05 bit [0,1] 0.05 bit [0,1] Determines the shape for the edges of the pulse Amplitude Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Defined as the time from when the rising edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Fall time Defined as the time from when the falling edge reaches 90% of the amplitude to the time it reaches 10% of the amplitude 15 NRZ PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 16 NRZ PULSE GENERATOR Technical background According to the parameter Rectangle shape, this model can produce pulses with different edge shapes: Exponential –( t ⁄ cr ) ⎧ ,0 ≤ t < t 1 ⎪1 – e ⎪ 1 ,t 1 ≤ t < t 2 E(t) = ⎨ ⎪ ⎪ e – ( t ⁄ c f ) ,t ≤ t < T 2 ⎩ Gaussian ⎧ – ( t ⁄ c r )2 ,0 ≤ t < t 1 ⎪ e ⎪ 1 ,t 1 ≤ t < t 2 E( t) = ⎨ ⎪ 2 ⎪ – ( t ⁄ cf ) e ,( t 2 ≤ t < T ) ⎩ 17 NRZ PULSE GENERATOR Linear ⎧ t ⁄ c r ,0 ≤ t < t 1 ⎪ E ( t ) = ⎨ 1, t 1 ≤ t < t 2 ⎪ ⎩ t ⁄ c f ,t 2 ≤ t < T Sine ⎧ sin ( π.t ⁄ c r ) ,0 ≤ t < t 1 ⎪ 1 ,t 1 ≤ t < t 2 E(t) = ⎨ ⎪ ⎩ sin ( π.t ⁄ c f ) ,t 2 ≤ t < T where cr is the rise time coefficient and cf is the fall time coefficient. t1 and t2, together with cr and cf, are numerically determined to generate pulses with the exact values of the parameters Rise time and Fall time, and T is the bit period. 18 GAUSSIAN PULSE GENERATOR Gaussian Pulse Generator Generates an electrical Gaussian-pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Order 1 — [1,100] False — True, False Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude Order of the function Truncated Determines whether or not the pulses overlap with each other 19 GAUSSIAN PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background This model generates Gaussian or super-Gaussian electrical pulses according to the bit sequence at the input. For each bit 2N 1 t.k – --- ⎛ ----------------⎞ ⎛ ⎞ 2 ⎝ T FWHM⎠ ⎜ E ( t ) = B. ⎜ A p .e + A bias⎟⎟ ⎝ ⎠ where Ap is the parameter peak-to-peak Amplitude, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient determined numerically to generate pulses with the exact values of the parameter Width TFWHM, and N is the Order of the Gaussian (N=1) or super-Gaussian pulses (N>1). 20 HYPERBOLIC-SECANT PULSE GENERATOR Hyperbolic-Secant Pulse Generator Generates a hyperbolic-secant pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Truncated False — Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Defines whether or not the pulses overlap with each other 21 HYPERBOLIC-SECANT PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background This model generates electrical pulses according to the bit sequence at the input. For each bit: t.k ⎞ 2 + A ⎞ E ( t ) = B. ⎛ A p ⁄ cosh ⎛ ----------------bias⎠ ⎝ ⎝T ⎠ FWHM where Ap is the parameter peak-to-peak Amplitude, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient determined numerically to generate pulses with the exact values of the parameter Width, TFWHM. 22 SINE GENERATOR Sine Generator Generates an electrical sine waveform signal. Ports Name and description Port type Signal type Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 32 GHz Hz, MHz, GHz, THz ]0,+INF[ 1 a.u. — ]-INF,+INF[ 0 a.u. — ]-INF,+INF[ 0 deg — ]-INF,+INF[ Frequency simulation window Amplitude Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Phase Initial phase of the signal 23 SINE GENERATOR Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window 24 TRIANGLE PULSE GENERATOR Triangle Pulse Generator Generates an electrical triangle-pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Truncated False — Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Determines whether or not the pulses overlap with each other 25 TRIANGLE PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 26 SAW-UP PULSE GENERATOR Saw-Up Pulse Generator Generates a saw-up signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Truncated False — Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Determines whether or not the pulses overlap with each other 27 SAW-UP PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 28 SAW-DOWN PULSE GENERATOR Saw-Down Pulse Generator Generates a saw-down pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit [-1, 1] Truncated False — True, False Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude Determines whether or not the pulses overlap with each other 29 SAW-DOWN PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 30 IMPULSE GENERATOR Impulse Generator Generates an electrical signal composed by a sequence of Impulses. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Position Relative position of the impulse Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 31 IMPULSE GENERATOR Notes: 32 RAISED COSINE PULSE GENERATOR Raised Cosine Pulse Generator Generates a raised-cosine pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Truncated False — Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Determines whether or not the pulses overlap with each other 33 RAISED COSINE PULSE GENERATOR Simulation Name and description Default value Default unit Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background This model generates electrical pulses according to the bit sequence at the input. For each bit: t.k ⎞ 2 + A ⎞ E ( t ) = B. ⎛ A p . cos ⎛ ----------------bias⎠ ⎝ ⎝T ⎠ FWHM where Ap is the parameter peak-to-peak Amplitude, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient determined numerically to generate pulses with the exact values of the parameter Width, TFWHM. 34 SINE PULSE GENERATOR Sine Pulse Generator Generates a sine-pulsed signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ 0.5 bit [0,1] Position 0 bit Truncated False — Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Determines whether or not the pulses overlap with each other 35 SINE PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background This model generates electrical pulses according to the bit sequence at the input. For each bit: t.k ⎞ + A ⎞ E ( t ) = B. ⎛ A p . cos ⎛ ----------------bias⎠ ⎝ ⎝T ⎠ FWHM where Ap is the parameter peak-to-peak Amplitude, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient numerically determinate to generate pulses with the exact values of the parameter Width TFWHM. 36 MEASURED PULSE Measured Pulse Generates an electrical pulse based on measurements according to the bit sequence at the input port. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Electrical Parameters Main Name and description Default value Default unit Value range Amplitude 1 a.u. ]-INF,+INF[ 0 a.u. ]-INF,+INF[ Position 0 bit Filename Pulse.dat — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Peak-to-peak amplitude of the pulse Bias DC Offset of the pulse Filename with the measured data Numerical Determines the interpolation algorithm for the measured data 37 MEASURED PULSE Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Graphs Name and description X Title Y Title Measured data Time period (a.u.) Amplitude (a.u.) Technical background This model generates electrical signal loading measurements from a file. The input file is formatted containing two values per line, the time in seconds and signal amplitude in arbitrary units. The time scale is normalized to fit in one bit period - the duration of the pulse. For example, the file representing one measurement has the following form: 0 0 1e-6 0.5 2e-6 0.5 3e-6 0 ... 38 MEASURED PULSE SEQUENCE Measured Pulse Sequence Generates an electrical signal based on measurements. Ports Name and description Port type Signal type Output Output Electrical Parameters Main Name and description Default value Default unit Value range Scale 1 a.u. ]-INF,+INF[ 0 s [0,+INF[ Sequence.dat — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Factor to scale the signal amplitude Start time Initial part of the signal to be skipped Filename Filename with the measured data Numerical Determines the interpolation algorithm for the measured data 39 MEASURED PULSE SEQUENCE Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window Graphs Name and description X Title Y Title Measured data Time (s) Amplitude (a.u.) Technical background This model generates electrical signal loading measurements from a file. The input file is formatted containing two values per line, the time in seconds and signal amplitude in arbitrary units. For example, the file representing one measurement has the following form: 0 0 1e-6 0.5 2e-6 0.5 3e-6 0 ... 40 BIAS GENERATOR Bias Generator A d.c. source. Ports Name and description Port type Signal type Output Output Electrical Parameters Main Name and description Default value Units Value range Amplitude 1 a.u. ]-INF,+INF[ Amplitude of the signal output Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window 41 BIAS GENERATOR Notes: 42 M-ARY PULSE GENERATOR M-Ary Pulse Generator Generates multilevel pulses according to the M-ary signal input. Ports Name and description Port type Signal type Input Input M-ary Output Output Electrical Parameters Main Name and description Default value Gain 0 Units Value range ]-INF,+INF[ Linear gain to be applied to the signal input Bias 1 a.u. ]-INF,+INF[ 1 bit [0,1] 0 bit DC Offset of the pulse Duty cycle Duration of the high level bit Position Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window 43 M-ARY PULSE GENERATOR Technical background This model generates pulses according to: ⎧ ⎪ b, 0 ≤ t < t 1 ⎪ v out ( t ) = ⎨ av in ( t ) + b, t 1 ≤ t < t 1 + t c ⎪ ⎪ b, t 1 + t c ≤ t < T ⎩ where v in is the input M-ary signal, a is the linear gain, and b is the parameter Bias. T is the bit period, t c is the duty cycle, and t 1 is the pulse position. 44 M-ARY RAISED COSINE PULSE GENERATOR M-ary Raised Cosine Pulse Generator Generates multilevel raised cosine pulses according to the M-ary signal input. Ports Name and description Port type Signal type Input Input M-ary Output Output Electrical Parameters Main Name and description Default value Gain 0 Units Value range ]-INF,+INF[ Linear gain to be applied to the signal input Bias 1 a.u. ]-INF,+INF[ 1 bit [0,1] Position 0 bit Roll off factor 1 [0,1] False True, False DC offset of the pulse Width Duration of the high level bit The raised cosine roll off factor Square root Determines whether or not the square root is enabled 45 M-ARY RAISED COSINE PULSE GENERATOR Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Sample rate Frequency simulation window Technical background This model generates pulses according to: ⎧ ⎪ b, 0 ≤ t < t 1 ⎪ v out ( t ) = ⎨ ah ( t ) + b, t 1 ≤ t < t 1 + w ⎪ ⎪ b, t 1 + w ≤ t < T ⎩ where v in is the input M-ary signal, a is the linear gain, and b is the parameter Bias. T is the bit period, w is the pulse width, and t 1 is the pulse position. h is given by: απt ⎛ sin ⎛ πt -----⎞⎠ cos ⎛⎝ ---------⎞⎠ ⎞ ⎝ ⎜ T T ⎟ h ( t ) = ⎜ -------------------------------------------⎟ 2 ⎜ πt - ⎛⎝ 1 – ⎛⎝ 2αt ---------⎞⎠ ⎞⎠ ⎟⎠ ⎝ ---T T If parameter Square root is enable, h is given by: sin ⎛ πt ----- ( 1 + α )⎞ ⎝ ⎠ T cos ⎛⎝ πt ----- ( 1 + α )⎞⎠ + ------------------------------------T 4αt --------T h ( t ) = 4α --------------------------------------------------------------------------------2 4αt ⎛ ⎞ ⎛ ⎞ π T 1 – --------⎝ ⎝ T ⎠ ⎠ 46 PREDISTORTION Predistortion Apply predistortion to electrical signals. The component can inversely model an optical modulator's amplitude and phase characteristics. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Predistortion Arcsin Units Arcsin, Polynomial Predistortion type Coefficients 1 Value range a.u. ]-INF,+INF[ Coefficients for Polynomial predistortion type Gain 1 ]-INF,+INF[ Linear gain to be applied to the signal Bias 0 a.u. ]-INF,+INF[ DC Offset of the signal Simulation Name and description Default value Default units Unit Value range Enabled True — — True, False Determines whether or not the component is enabled 47 PREDISTORTION Technical background If parameter Predistortion is Arcsin, the function applied to the input signal is: v out ( t ) = --1- arc sin ( v in ( t ) ) ⋅ a + b π where v in is the input signal, a is the linear gain, and b is the bias. If parameter Predistortion is Polynomial, the function applied to the input signal is: v out ( t ) = ( c 0 + c 1 v in ( t ) + c 2 v ( t ) where 48 N 2 in + … + c N v ( t ) in ) ⋅ a + b c i is the polynomial coefficient of index i. OPTICAL GAUSSIAN PULSE GENERATOR Optical Gaussian Pulse Generator Generates a Gaussian-pulsed optical signal. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ –100 dBm W, mW, dBm ]-INF,+INF[ 0.5 bit — [0,1] Position 0 bit — Order 1 — — [1,100] False — — True, False Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude Order of the function Truncated Determines whether or not the pulses overlap with each other 49 OPTICAL GAUSSIAN PULSE GENERATOR Chirp Name and description Default value Default unit Value range Chirp definition Linear — Linear, Measured Chirp factor 0 rad/s Alpha parameter 0 rad/W Adiabatic chirp 0 1/s [0,1] Name and description Default value Default unit Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Results from changes in the steady state carrier densities Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Parameterized Parameterized — — Sample rate Sample rate Hz Hz, GHz, THz Determines whether or not the component is enabled Frequency simulation window 50 ]0,+INF[ OPTICAL GAUSSIAN PULSE GENERATOR Technical background This model generates Gaussian or super-Gaussian optical pulses according to the bit sequence at the input. For each bit, the output optical power is: 2N 1 t.k – --- ⎛ ----------------⎞ ⎛ ⎞ 2 ⎝ T FWHM⎠ ⎜ P ( t ) = B. ⎜ A p .e + Abias⎟⎟ ⎝ ⎠ where Ap is the parameter peak-to-peak Power, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient determined numerically to generate pulses with the exact values of the parameter Width, TFWHM, and N is Order of the Gaussian (N=1) or super-Gaussian pulses (N>1). The chirp is modeled using: α d dϕ ------ = ------e ----- ln P ( t ) + κP ( t ) 2 dt dt where ϕ is the signal phase, αe is the parameter Linewidth enhancement factor, and κ is the parameter Adiabatic chirp. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y where the power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 51 OPTICAL GAUSSIAN PULSE GENERATOR Notes: 52 OPTICAL SECH PULSE GENERATOR Optical Sech Pulse Generator Generates a hyperbolic-secant pulsed optical signal. Ports Name and description Port type Signal type Bit sequences Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ –100 dBm W, mW, dBm ]-INF,+INF[ 0.5 bit — [0,1] Position 0 bit — Truncated False — — Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude True, False Determines whether or not the pulses overlap with each other 53 OPTICAL SECH PULSE GENERATOR Chirp Name and description Default value Default unit Value range Chirp definition Linear — Linear, Measured Chirp factor 0 rad/s Alpha parameter 0 rad/W Adiabatic chirp 0 1/s [0,1] Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Results from changes in the steady state carrier densities Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Parameterized Parameterized — — Sample rate Sample rate Hz Hz, GHz, THz Determines whether or not the component is enabled Frequency simulation window 54 ]0,+INF[ OPTICAL SECH PULSE GENERATOR Technical background This model generates optical pulses according to the bit sequence at the input. For each bit, the output optical power is: t.k ⎞ + A ⎞ P ( t ) = B. ⎛⎝ A p ⁄ cosh ⎛⎝ ------------bias⎠ T FWHM⎠ where Ap is the parameter peak-to-peak Power, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. k is the fitting coefficient determined numerically to generate pulses with the exact values of the parameter Width, TFWHM. The chirp is modeled using: α d dϕ ------ = ------e ---- ln P ( t ) + κP ( t ) dt 2 dt where ϕ is the signal phase, αe is the parameter Linewidth enhancement factor, and κ is the parameter Adiabatic chirp. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 55 OPTICAL SECH PULSE GENERATOR Notes: 56 OPTICAL IMPULSE GENERATOR Optical Impulse Generator Generates an optical signal composed by a sequence of Impulses. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ –100 dBm W, mW, dBm ]-INF,+INF[ 0 bit Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Position [0,1] Relative position of the impulse Chirp Name and description Default value Units Alpha parameter 0 rad/W Adiabatic chirp 0 1/s Value range [0,1] Results from changes in the steady state carrier densities 57 OPTICAL IMPULSE GENERATOR Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Parameterized Parameterized — — Sample rate Sample rate Hz Hz, GHz, THz Determines whether or not the component is enabled Frequency simulation window 58 ]0,+INF[ OPTICAL IMPULSE GENERATOR Technical background This model generates optical pulses according to the bit sequence at the input. For each bit, the output optical power is: P ( t ) = B. ( Ap δ ( t – t p ) + A bias ) where Ap is the parameter peak-to-peak Power, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. δ is the impulse function and tP is the parameter Pulse position. The chirp is modeled using: α d dϕ ------ = ------e ---- ln P ( t ) + κP ( t ) dt 2 dt where ϕ is the signal phase, αe is the parameter Linewidth enhancement factor, and κ is the parameter Adiabatic chirp. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ ) tan ( 2α ) = 2 ----------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 59 OPTICAL IMPULSE GENERATOR Notes: 60 MEASURED OPTICAL PULSE Measured Optical Pulse Generates a pulse based on measurements. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ –100 dBm W, mW, dBm ]-INF,+INF[ Position 0 bit — Filename Optical pulse.dat — — — Power — — Power, Power Phase, Real Imag, Phase Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Filename with the measured data File format Determines the format of the file with the measurements 61 MEASURED OPTICAL PULSE Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Numerical Determines the interpolation algorithm for the measured data Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Parameterized Parameterized — — Sample rate Sample rate Hz Hz, GHz, THz Determines whether or not the component is enabled Frequency simulation window Graphs Name and description X Title Y Title Measured magnitude data Time period (a.u.) Amplitude (V) Measured phase data Time period (a.u.) Phase (rad) 62 ]0,+INF[ MEASURED OPTICAL PULSE Technical background The input file is formatted containing two items per line — the time in seconds and the signal measurement (Power in watts, Phase in radians, Real and Imag in Volts). The time scale is normalized to fit in one bit period - the duration of the pulse. According to the parameter File format, the second item can be one value (Power or Phase), or two values (Power and Phase or Real and Imag). Power (Phase will be set to zero) 0 0 1e-6 0.5 2e-6 0.5 3e-6 0 ... Power Phase 0 0 0 1e-6 0.5 3.14 2e-6 0.5 3.14 3e-6 0 0 0 0 0 1e-6 –0.5 7.9e-4 2e-6 –0.5 7.9e-4 3e-6 0 0 ... Real Imag ... 63 MEASURED OPTICAL PULSE Phase (Power will be set to one) 0 0 1e-6 3.14 2e-6 3.14 3e-6 0 ... This model generates optical pulses according to the bit sequence at the input. For each bit, the output optical power is: P ( t ) = B. ( A p M ( t ) + A bias ) where Ap is the parameter peak-to-peak Power, and Abias is the parameter Bias. B is the bit value (1 or 0) and depends on the input bit sequence. M is the measured data. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 64 MEASURED OPTICAL PULSE SEQUENCE Measured Optical Pulse Sequence Generates an optical signal based on measurements. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 1 a.u. — ]-INF,+INF[ 0 s — [0,+INF[ Sequence.dat — — — Power — — Power, Power Phase, Real Imag, Phase Name and description Default value Units Value range Azimuth 0 deg ]-90,90] Emission frequency Scale Factor to scale the signal amplitude Start time Initial part of the signal to be skipped Filename Filename with the measured data File format Determines the format of the file with the measurements Polarization Azimuth angle of output polarization 65 MEASURED OPTICAL PULSE SEQUENCE Name and description Default value Units Value range Ellipticity 0 deg [-45,45] Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Ellipticity angle of output polarization Numerical Determines the interpolation algorithm for the measured data Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — Sampled, Parameterized Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Graphs Name and description X Title Y Title Measured magnitude data Time (s) Amplitude (V) Measured phase data Time (s) Phase (rad) 66 MEASURED OPTICAL PULSE SEQUENCE Technical background This model generates optical signal loading measurements from a file. The input file is formatted containing two items per line — the time in seconds and signal measurement (Power in watts, Phase in radians, Real and Imag in Volts). According to the parameter File format, the second item can be one value (Power or Phase) or two values (Power and Phase or Real and Imag). Power (Phase will be set to zero) 0 0 1e-6 0.5 2e-6 0.5 3e-6 0 ... Power Phase 0 0 0 1e-6 0.5 3.14 2e-6 0.5 3.14 3e-6 0 0 0 0 0 1e-6 –0.5 7.9e-4 2e-6 –0.5 7.9e-4 3e-6 0 0 ... Real Imag ... 67 MEASURED OPTICAL PULSE SEQUENCE Phase (Power will be set to one) 0 0 1e-6 3.14 2e-6 3.14 3e-6 0 ... The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 68 TIME RESOLVE CHIRP (TRC) MEASUREMENT DATA Time Resolve Chirp (TRC) Measurement Data This component is an interface between OptiSystem and time resolve chirp (TRC) [1] measurement instruments, such as the OSA Agilent 86146B with TRC option. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 1 a.u. — ]-INF,+INF[ 0 s — [0,+INF[ Sequence.dat — — — Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Emission frequency Scale Factor to scale the signal amplitude Start time Initial part of the signal to be skipped Filename Filename with the measured data Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization 69 TIME RESOLVE CHIRP (TRC) MEASUREMENT DATA Numerical Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Determines the interpolation algorithm for the measured data Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — Sampled, Parameterized Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Graphs Name and description X Title Y Title Measured power data Time (s) Power (W) BER measured chirp data Time (s) Chirp (Hz) Technical background This component generates optical signal loading measurements from a file. These measurements are TRC data that describe the power and chirp evolution of the optical signal in time [1]. TRC provides frequency vs. time information about a modulated lightwave signal. Also called dynamic chirp, the TRC graph provides useful information on the ability of a modulated signal to propagate over long distances in optical fiber. Using measurement equipment such as the Agilent 86146B, with the filter mode capability, Agilent 86100 Infinium Digital Communications Analyzer (DCA) dedicated software (86146B Option TRL), and a personal computer, the time resolved chirp (TRC) of a modulated laser can be calculated. From the measurement, a file with the TRC data is generated. OptiSystem can load this file and the effect of laser chirp on a wide variety of system performance metrics 70 TIME RESOLVE CHIRP (TRC) MEASUREMENT DATA - such as the effect on the performance of a long-haul dense wavelength division multiplexed (DWDM) system with EDFA and Raman optical amplification and dispersion compensation - can be studied across an unlimited range of system designs. The input file is formatted containing three items per line - the time in seconds, the signal power is Watt (Linear scale) or dBm, and the signal chirp (Hz). Time Signal power (W or dBm) Signal chirp 0 1.27617e-006 -7.80425e+009 6.25e-012 1.139e-006 -4.94806e+009 1.25e-011 1.46161e-006 -6.57706e+009 1.875e-011 1.33136e-006 -6.10874e+009 2.5e-011 1.54705e-006 -2.89844e+009 3.125e-011 1.03595e-006 -7.38826e+009 ... ... ... The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 71 TIME RESOLVE CHIRP (TRC) MEASUREMENT DATA Reference: [1] Agilent Technologies, “Making Time-Resolved Chirp Measurements Using the Optical Spectrum Analyzer and Digital Communications Analyzer”, Agilent Application Note 1550-7, 2002. 72 SPATIAL OPTICAL GAUSSIAN PULSE GENERATOR Spatial Optical Gaussian Pulse Generator This component is Gaussian pulse generator that includes transverse mode profiles in the optical output. It is a subsystem built using the Optical Gaussian Pulse and the Multimode Generators. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [10, 10000] 0 dBm W, mW, dBm [-1000, 1000] –100 dBm W, mW, dBm [-1000, 1000] 0.5 bit [0, 1] 0 bit [-1,1] Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude Position Relative position of the impulse Order 1 [1, 100] NO [YES, NO] Order of the function Truncated Determines whether or not the pulses overlap with each other 73 SPATIAL OPTICAL GAUSSIAN PULSE GENERATOR Chirp Name and description Default value Default unit Units Value range Chirp definition Linear Chirp factor 0 rad/s [-1000, 1000] Alpha parameter 0 rad/W [-1000, 1000] Adiabatic chirp 0 1/s [-1000, 1000] [Linear, Measured] Results from changes in the steadystate carrier densities Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90, 90] 0 deg [-45, 45] Default unit Units Value range Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Spatial Effects Name and description Default value Power ratio array 1 List of power values that describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size Spot size for X polarization 74 5 um [1e-100, 1e+100] SPATIAL OPTICAL GAUSSIAN PULSE GENERATOR Name and description Default value Default unit Units Value range Pol. X inv. radius of curvature 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for polarization Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NOT] Determines whether or not the component is enabled Sample rate Sample rate Hz Hz, GHz, THz [1, 1e+100] Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Frequency simulation window Space width X Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The layout of the Spatial Optical Gaussian Pulse Generator is presented in Figure 1. Refer to Optical Gaussian Pulse Generator and Multimode Generator component documentation for the technical background of the models. 75 SPATIAL OPTICAL GAUSSIAN PULSE GENERATOR Figure 1 Spatial Optical Gaussian Pulse Generator subsystem 76 SPATIAL OPTICAL SECH PULSE GENERATOR Spatial Optical Sech Pulse Generator This component is sech pulse generator that includes transverse mode profiles in the optical output. It is a subsystem built using a the Optical Sech Pulse and the Multimode Generators. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [10, 10000] 0 dBm W, mW, dBm [-1000, 1000] –100 dBm W, mW, dBm [-1000, 1000] 0.5 bit [0, 1] 0 bit [-1, 1] Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Width FWHM of the pulse amplitude Position Relative position of the impulse Truncated NO [YES, NO] Determines whether or not the pulses overlap with each other 77 SPATIAL OPTICAL SECH PULSE GENERATOR Chirp Name and description Default value Default unit Units Value range Chirp definition Linear Chirp factor 0 rad/s [-1000, 1000] Alpha parameter 0 rad/W [-1000, 1000] Adiabatic chirp 0 1/s [-1000, 1000] [Linear, Measured] Results from changes in the steadystate carrier densities Polarization Name and description Default value Units Value range Azimuth 0 deg [-90, 90] 0 deg [-45, 45] Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Spatial Effects Name and description Default value Power ratio array 1 Default unit Units Value range List of power values which describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size Spot size for X polarization 78 5 um [1e-100, 1e+100] SPATIAL OPTICAL SECH PULSE GENERATOR Name and description Default value Default unit Units Value range Pol. X inv. radius of curvature 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NOT] Determines whether or not the component is enabled Sample rate Sample rate Hz Hz, GHz, THz [1, 1e+100] Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Frequency simulation window Space width X Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The layout of the Spatial Optical Sech Pulse Generator is presented in Figure 1. Refer to Optical Sech Pulse Generator and Multimode Generator component documentation for the technical background of the models. 79 SPATIAL OPTICAL SECH PULSE GENERATOR Figure 1 80 Spatial Optical Sech Pulse Generator subsystem SPATIAL OPTICAL IMPULSE GENERATOR Spatial Optical Impulse Generator This component is impulse generator that includes transverse mode profiles in the optical output. It is a subsystem built using a the Impulse and the Multimode Generators. Ports Name and description Port type Signal type Bit sequence Input Binary Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 nm Hz, THz, nm [10, 10000] 0 dBm W, mW, dBm [-1000, 1000] –100 dBm W, mW, dBm [-1000, 1000] 0 bit Emission frequency Power Peak-to-peak power of the pulse Bias DC Offset of the pulse Position [-1, 1] Relative position of the impulse Chirp Name and description Default value Default unit Alpha parameter 0 rad/W Units Value range [-1000, 1000] 81 SPATIAL OPTICAL IMPULSE GENERATOR Name and description Default value Default unit Adiabatic chirp 0 1/s Units Value range [-1000, 1000] Results from changes in the steadystate carrier densities Polarization Name and description Default value Units Value range Azimuth 0 deg [-90, 90] 0 deg [-45, 45] Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Spatial Effects Name and description Default value Power ratio array 1 Default unit Units Value range List of power values that describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array List of mode indexes 'l,m' for Y polarization 82 00 SPATIAL OPTICAL IMPULSE GENERATOR Name and description Default value Default unit Units Value range Pol. Y spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for polarization Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NOT] Determines whether or not the component is enabled Sample rate Sample rate Hz Hz, GHz, THz [1, 1e+100] Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Frequency simulation window Space width X Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The layout of the Spatial Optical Impulse Generator is presented in Figure 1. Refer to Optical Impulse Generator and Multimode Generator component documentation for the technical background of the models. Figure 1 Spatial Optical Impulse Generator subsystem 83 SPATIAL OPTICAL IMPULSE GENERATOR Notes: 84 CW LASER CW Laser Generates a continuous wave (CW) optical signal. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz,THz, nm [0,+INF[ Power 0 dBm W, mW, dBm ]-INF,+INF[ Linewidth 10 MHz — [0,+INF[ Initial phase 0 deg — ]-INF,+INF[ MxN next generation — — — — StringParameter — — — — Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Emission frequency Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization 85 CW LASER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — Sampled, Parameterized Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Name and description Default value Default unit Units Value range Noise bandwidth 0 THz Hz, THz, nm [0,+INF[ –100 dB — ]-INF,+INF[ 3 dB — ]-INF,+INF[ Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Noise Bandwidth to create noise bins Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 86 CW LASER Technical background In the CW case, the average output Power is a parameter that you specify. Laser phase noise is modeled using the probability density function: Δϕ 2 4πΔfdt 1 - ⋅ e – ----------------f ( Δϕ ) = --------------------2π Δfdt where Δϕ is the phase difference between two successive time instants and dt is the time discretization. A Gaussian random variable for the phase difference between two successive time instants with zero mean and a variance equal to assumed, with Δf 2 π Δ f has been as the laser Linewidth. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y where the power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as follows: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2------------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 87 CW LASER Notes: 88 LASER RATE EQUATIONS Laser Rate Equations Utilizes the rate equations to simulate the modulation dynamics of a laser. Ports Name and description Port type Signal type Modulation Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Unit Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] True — — True, False 10 dBm W, mW, dBm [-1e100, 1e100] 0 dBm W, mW, dBm [-1e100, 1e100] 38 mA — [0, 1000] Emission frequency of the laser Calculate current Defines whether to estimate the input bias and peak current to achieve the user defined steady Power Steady state power at the peak current Power at bias current Steady state power at the bias current Bias current Input bias current 89 LASER RATE EQUATIONS Name and description Default value Default unit Unit Value range Modulation peak current 23 mA — [0, 1000] 33.4572 mA — [0, 1000] 0.0155558 mW — [0, 1000] Name and description Default value Default unit Value range Active layer volume 1.5e-010 cm3 0, 1e-3 Quantum efficiency 0.4 — 0, 1 Group velocity 8.5e+009 cm/s 0, 100e9 Differential gain coefficient 2.5e-016 cm2 0, 50e-16 Carrier density at transparency 1e+018 cm-3 0, 100e18 Mode confinement factor 0.4 — 0, 1 Recombination model Lifetime — Lifetime, Coefficients Carrier lifetime 1e-009 s 0, 50e-9 Recombination coefficient A 100000000 1/s 0, 1e15 3e-029 cm^3/s 0, 1e-7 1e-009 cm^6/s 0, 1e-7 Photon lifetime 3e-012 s 0, 50e-9 Differential gain coefficient 2.5e-016 cm2 0, 50e-16 Photon lifetime 3e-012 — 0, 50e-9 Spontaneous emission factor 3e-005 — 2e-5, 20e-5 Gain compression coefficient 1e-017 cm3 0.5e-17, 10e17 Input modulation peak current Threshold current The threshold current, calculated from the laser physical parameters Threshold power The threshold power, calculated from the laser physical parameters Physical Linear recombination coefficient Recombination coefficient B Bimolecular recombination coefficient Recombination coefficient C Auger recombination coefficient 90 LASER RATE EQUATIONS Name and description Default value Default unit Value range Linewidth enhancement factor 5 — –20, 20 Mode confinement factor 0.4 — 0, 1 Carrier lifetime 1e-009 s 0, 50e-9 Photon lifetime 3e-012 s 0, 50e-9 Name and description Default value Units Value range Adaptive step False — True, False 1000000 — [1e3,10e6] 0.0001 — — Name and description Default value Units Value range Calculate graphs False True, False 20 [5, 100e6] Numerical Defines whether to use adaptive step or not Max. number of steps The maximum number of steps Relative error Relative integration error Graphs Defines whether to calculate graphs or not Number of points Number of points for the graphs From 0 mA [0, +INF] 40 mA [0, +INF] Name and description Default value Units Value range Enabled True — True, False Parameterized Parameterized — — Current lower limit for the graphs To Current upper limit for the graphs Simulation 91 LASER RATE EQUATIONS Noise Name and description Default value Units Value range Include noise True — True, False Include phase noise True — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The modulation dynamics of the laser are modeled by coupled rate equations which describe the relation between the carrier density N ( t ) , photon density S ( t ) , and optical phase φ ( t ) : dN ( t )- = ---------I ( t )- – N ( t ) – g ⋅ ( N ( t ) – N ) ⋅ -----------------------------1 ---------------------- ⋅ S(t) o t dt q⋅V τn ( 1 + ε ⋅ S( t) ) 1 S(t) + Γ ⋅ β ⋅ N ( t )dS ( t )- = Γ ⋅ g ⋅ ( N ( t ) – N ) ⋅ ------------------------------ ⋅ S ( t ) – -------------------------------------------o t (1 + ε ⋅ S(t)) τp τn dt dφ ( t )- = 1--- ⋅ α ⋅ Γ ⋅ g ⋅ ( N ( t ) – N ) – ---1-----------o t dt 2 τp where go is the gain slope constant, g o = v g ⋅ a o a0 vg ε 92 is the active layer coefficient is the group velocity is the gain compression factor Nt is the carrier density at transparency β is the fraction of spontaneous emission coupled into the lasing mode (2) (3) (4) LASER RATE EQUATIONS Γ V τp τn α is the mode confinement factor is the active layer volume is the photon lifetime is the electron lifetime is the linewidth enhancement factor The optical power and chirp response of the semiconductor laser to a current waveform I ( t ) is determined by the above equations. Parameters Bias current and Modulation peak current are scale factors applied to the input electrical signal. The internal current I ( t ) is given by: I ( t ) = I DC + I in ( t ) × I Pk Where I in ( t ) is the input signal current, (5) I DC is the parameter Bias Current and I Pk is the parameter Modulation peak current. If parameter Bias Current and Modulation peak current have zero values, the internal current is given by I in ( t ) only. A Runge-Kutta algorithm is used to numerically integrate the coupled first order differential equations (2-4). If parameters Include noise and Include phase noise are disabled, these equations apply to a noiseless laser oscillating in a single longitudinal mode above threshold. The photon and electron densities within the active region of the laser are assumed to be uniform. If parameter Include noise is enabled, the Langevin noise terms for photon and electron densities are included in the model[2]. If Include phase noise is enabled, the Langevin noise term for the phase is included in the model. The linewidth enhancement factor and the nonlinear gain compression parameter are taken to be constant for a given structure. The time variations for the optical and laser chirp are: S ⋅ V ⋅ ηo ⋅ h ⋅ v P = ----------------------------------2 ⋅ Γτ p (6) 1 - ⋅ dφ Δv = -------------2 ⋅ π dt (7) 93 LASER RATE EQUATIONS η o is the differential quantum efficiency where v h is the optical frequency is the Planck’s constant The Laser Rate Equations supports individual samples for time-driven simulation. References [1] J. C. Cartledge and G. S. Burley, “The Effect of the Laser Chirping on Lightwave System Performance”, J. Lightwave Technology, vol. 7, pp. 568-573, March 1989. [2] Agrawal GP, Dutta NK. Semiconductor lasers, 2nd ed. New York: Van Nostrand Reinhold, 1993. 94 LASER MEASURED Laser Measured Extracts values of the rate equation parameters using measurements and simulates the modulation dynamics of a laser. Ports Name and description Port type Signal type Modulation Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] True — — True, False 10 dBm W, mW, dBm [-1e100, 1e100] 0 dBm W, mW, dBm [-1e100, 1e100] 23 mA — [0, 1000] 28 mA — [0, 1000] Emission frequency of the laser Calculate current Defines whether to estimate the input bias and peak current to achieve the user defined steady Power Steady state power at the peak current Power at bias current Steady state power at the bias current Bias current Input bias current Modulation peak current Input modulation peak current 95 LASER MEASURED Measurements Name and description Default value Default unit Units Value range Frequency response data type Parameters — — Parameters, From file 10.28 1e9 s-1 — ]0, 1000] 6.43 1e20 Hz2 — ]0, 1000] 6.43 1e20 Hz2 — ]0, 1000] 18 mA — [0, 1000] 23 mA — [0, 1000] True — — True, False 0.3 mW/mA — [1e-100, 1e100] 1.5 mW W, mW, dBm [1e-100, 1e100] False — — True, False 10 MHz — [1,200] False — — True, False 0.5 ns — [1e-5, 100] The measured damping factor of the laser Damping factor The measured damping factor of the laser Resonance frequency factor The measured defined resonance frequency factor Subtracted IM response filename The measured defined resonance frequency factor Threshold current The measured threshold current of the laser Reference current The reference current used to estimate the measured output power Slope efficiency data Defines whether to use slope efficiency or power to estimate the LI curve Slope efficiency The measured slope efficiency of the laser Power at reference current The laser power at the reference current Linewidth data Determines whether the linewidth will be part of the parameter extraction procedure Linewidth Specifies the laser linewidth for the steady-state condition Turn-on delay data Determines whether the turn-on delay will be part of the parameter extraction procedure Turn-on delay Specifies the laser turn-on delay 96 LASER MEASURED Name and description Default value Default unit Units Value range Average RIN data False — — True, False 0.2 GHz — [0.01,20] 15 GHz — [0.01,20] -140 dB/Hz — [-500, -50] Determines whether the average RIN in a specified bandwidth will be part of the parameter extraction procedure RIN start Specifies the initial frequency of the frequency range where the average RIN is calculated RIN stop Specifies the final frequency of the frequency range where the average RIN is calculated Average RIN Specifies the average RIN value for the steadystate condition over the frequency bandwidth defined by the values of RIN start and stop. Initial estimate Name and description Default value Default unit Value range Group velocity 8.5e+009 cm/s 0, 100e9 Calculate parameters True — Linewidth enhancement factor 5 — –20, 20 Active layer volume estimation 2e-011 cm3 0, 1e-3 Quantum efficiency estimation 0.2 — 0, 1 Carrier density at transparency estimation 1e+018 cm-3 0, 100e18 Differential gain coefficient estimation 1.765e-016 cm2 0, 50e-16 Mode confinement factor estimation 0.2 — 0, 1 Recombination model Lifetime — Lifetime, Coefficients Recombination coefficient A estimation 1e-009 s 0, 50e-9 100000000 1/s 0, 50e-9 3e-029 cm^3/s 0, 50e-9 Defines whether to optimize the laser physical parameters to achieve the target measurement or not. Linear recombination coefficient Recombination coefficient B estimation Bimolecular recombination coefficient Recombination coefficient C estimation Auger recombination coefficient 97 LASER MEASURED Name and description Default value Default unit Value range Auger recombination coefficient estimation 1e-009 cm^6/s 0, 50e-9 Photon lifetime estimation 1e-012 s 0, 50e-9 Spontaneous emission factor estimation 0.0001 — 2e-5, 20e-5 Gain compression coefficient estimation 1.5e-017 cm3 0.5e-17, 10e-17 Numerical Name and description Default value Units Value range Adaptive step False — True, False 1000000 — [1e3,10e6] 0.0001 — — Name and description Default value Units Value range Calculate graphs False True, False 20 [5, 100e6] Defines whether to use adaptive step or not Max. number of steps The maximum number of steps Relative error Relative integration error Graphs Defines whether to calculate graphs or not Number of points Number of points for the graphs From 0 mA [0, +INF] 40 mA [0, +INF] Current lower limit for the graphs To Current upper limit for the graphs Simulation Name and description Default value Units Value range Enabled True — True, False Parameterized — — Determines whether or not the component is enabled Parameterized 98 LASER MEASURED Noise Name and description Default value Units Value range Include noise True — True, False Include phase noise True — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The laser measured model extracts values of the rate equation parameters using measurements of the threshold current, optical power, resonance frequency, and damping factor to simulate a DFB laser. Based on the results featured in [1], the values of the rate equation parameters are calculated in a way that parameters simultaneously yield the measured values of Y (damping factor), Z (resonance frequency factor), Ith (threshold current), and P (Power bias). The parameter extraction procedure is based on minimization of the sum of squared errors between the measured values of (Y, Z, Ith, P) and values calculated from rate equation parameters. The minimization is over the values of the rate equation parameters which are: Damping factor S - + ---1- – Γ ⋅ g ( N – N ) -------------------------1 1Y = g 0 ----------------------+ ---0 t 2 τ τ (1 + ε ⋅ S) n p (1 + ε ⋅ S) Resonance frequency factor g0 S - ⋅ ---1- + ( β – 1 ) ⋅ Γ ⋅ ---1 1 + ------------Z = g 0 ----------------------- g 0 ( N – N t ) -------------------------2 τ ⋅τ τn ( 1 + ε ⋅ S ) τp p n (1 + ε ⋅ S) Threshold current + N t ⋅ Γ ⋅ go ⋅ τp ⋅ V- ⋅ 1----------------------------------------I th = q---------τn Γ ⋅ go ⋅ τp 99 LASER MEASURED Power bias S ⋅ V ⋅ η0 ⋅ h ⋅ v P = ----------------------------------2 ⋅ Γτ p where go is the gain slope constant, g o = v g ⋅ a o a0 ε is the active layer coefficient is the gain compression factor Nt β Γ η0 V τp τn is the carrier density at transparency is the fraction of spontaneous emission coupled into the lasing mode is the mode confinement factor is the differential quantum efficiency is the active layer volume is the photon lifetime is the electron lifetime NandS are the steady-state values of the carrier and photon densities corresponding to the bias current of the laser v vg h is the unmodulated optical frequency is the group velocity is the Planck’s constant The minimization routine finds a local minimum for the equation 2 2 2 Func = ( Y mea – Y cal ) + ( z mea – z cal ) + ( P mea – P cal ) + ( I mea – I cal ) 2 where ( Y mea, Zmea ,Pmea ,I mea ) are the measured values and ( Y cal, Z cal ,P cal ,I cal ) are the calculated values using the initial estimates of the rate equation parameters. The parameters available in the main tab allow the user to enter the values for current, or for power in steady state. Using these numbers, the model will estimate the values of the current. Note: It is recommended to enter the values for current, rather than power, when using the measured laser (as this is the realistic case). The parameters in the measured tab are used to extract the physical/geometrical properties of the laser. This extraction is completely independent of the parameters in the main tab (current/power). After finding the rate equation parameters, the laser measured works similarly to the laser rate equations model. RIN is calculated according to [2][3]. 100 LASER MEASURED The internal current I ( t ) is given by: I ( t ) = I DC + I in ( t ) × I Pk Where I in ( t ) is the input signal current, (1) I DC is the parameter Bias Current and I Pk is the parameter Modulation peak current. If parameter Bias Current and Modulation peak current have zero values, the internal current is given by I in ( t ) only. The user can also calculate the subtracted IM response from the measured IM response curves (Figure1) and load a file with this information into the component. This will allow a pre-optimization step, where the component fits the parameters Z and Y to the measured results. Figure 1 Measured IM responses The file format for the subtracted IM response data is the following: Frequency0 SubtractedIM0 Frequency1 SubtractedIM1 Frequency2 SubtractedIM2 101 LASER MEASURED ... FrequencyN SubtractedIMN The units are GHz and dB respectively. The laser measured can also include the turn-on delay parameter in the optimization process. In this case, the turn-on delay value specified defines the time needed for the carrier density to reach the threshold carrier density when the laser current rises to the reference current. The calculation of the turn-on delay is based on the definition find in [1].The laser linewidth parameter can be included in the optimization process by defining the linewidth value for the laser when the bias current is the reference current parameter [4]. The RIN is calculated according to [2][3] and the user has to define the average RIN value in the defined frequency range. If parameter Include noise is enabled, the Langevin noise terms for photon and electron densities are included in the model[4]. If Include phase noise is enabled, the Langevin noise term for the phase is included in the model. The Laser Measured supports individual samples for time-driven simulation. Reference: [1] Cartledge, J. C. and Srinivasan, R. C. “Extraction of DFB laser rate equation parameters for system simulation purposes”, J. Light. Techn., 15, 852-860, (1997). [2] Yamada, M. "Variation of intensity noise and frequency noise with the spontaneous emission factor in semiconductor lasers". IEEE Journal of Quantum Electronics. Volume 30, Issue 7, July 1994 Page(s):1511 - 1519. [3] Agrawal, G.P., Fiber-Optic Communication Systems, Second edition. John Wiley & Sons, Inc., N.Y., (1997). [4] Agrawal GP, Dutta NK. Semiconductor lasers, 2nd ed. New York: Van Nostrand Reinhold, 1993. [5] K.Petermann, Laser Diode Modulation and Noise, Kluwer Academic Publishers,1988 102 LED LED Simulates a modulated LED. Ports Name and description Port type Signal type Modulation Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] Electron lifetime 1e-009 s — ]0, 1] RC constant 1e-009 s — ]0, 1] Quantum efficiency 0.05 — — ]0, 1] Bandwidth 6 THz Hz, THz, nm ]0, INF] Name and description Default value Units Value range Enabled True — True, False Parameterized Parameterized — — Iterations Iterations — [1, 1e+009] Simulation Determines whether or not the component is enabled 103 LED Random numbers Name and description Default value Units Value range Generate random seed Yes — True, False 0 — [0,4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background In this model, the mean of the optical power is a function of the modulation current (input signal). The conversion of the current into optical power is described by the responsivity of the LED: ( t )P = η ⋅ h ⋅ f ⋅ i------q where h f q i(t) η is the quantum efficiency is the Planck’s constant is the emission frequency is the electron charge is the modulation current signal The modulated characteristics depend of the electron lifetime and the device of the diode, and are modeled by the transfer function applied to the current: 1 H ( f ) = ----------------------------------------------------------1 + j ⋅ 2 ⋅ π ⋅ f ⋅ ( τ n + τ rc ) where τ n is the Electron life time and τ rc is the RC constant. If the parameter Parameterized is selected, the output consist of a single value representing the average LED output at the frequency output. Note: The noise bins signals are not produced by this modulator. 104 WHITE LIGHT SOURCE White Light Source Generates a gaussian distributed optical white noise. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ True — — True, False –30 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Sample rate Hz Hz, GHz, THz ]0,+INF[ Emission frequency PSD Determines whether the Power is the PSD (/Hz) or the average power Power Average output powers Simulation Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window 105 WHITE LIGHT SOURCE Noise Name and description Default value Default unit Units Value range Noise bins spacing 10 GHz Hz, GHz, THz, nm [1, 100000] Convert noise bins Convert noise bins — — — Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The average output Power or Power spectral density and Frequency are parameters that you specify. This model generates noise bins or sampled signals at the output according to: A Gaussian distribution has been assumed to describe the probability density function for the real and imaginary part of Ex and Ey. P is the average power when PSD parameter is false. If PSD is true, then P is calculated from the power spectral density multiplied by the Sample rate. 106 PUMP LASER Pump Laser Generates an optical parameterized signal to be used for optical amplifier pumping. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 980 nm Hz, THz, nm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Emission frequency Power Average output powers Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization 107 PUMP LASER Simulation Name and description Default value Units Value range Enabled True — True, False Iterations — [1, 1e+009] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Technical background In the CW Laser case, average output Power is a parameter that you specify. This model generates only parameterized signal at the output. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛⎜ 1 – k⎞⎟ ⋅ P ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y where the power splitting k and the phase difference θ are related to the parameters Azimuth α and Ellipticity ε as follows: k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2------------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) 108 PUMP LASER ARRAY Pump Laser Array An array of pump lasers. Ports Name and description Port type Signal type Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Units Value range Number of output ports 8 — [1, 1000] Frequency Name and description Frequency[0] Units Value Default value Default unit 1405 nm Hz, THz, nm [100, 2000] 1412.5 nm Hz, THz, nm [100, 2000] range Center frequency for pump 0 Frequency[1] Center frequency for pump 1 109 PUMP LASER ARRAY Name and description Frequency[2] Units Value Default value Default unit 1420 nm Hz, THz, nm [100, 2000] 1427.5 nm Hz, THz, nm [100, 2000] 1435 nm Hz, THz, nm [100, 2000] 1442.5 nm Hz, THz, nm [100, 2000] 1450 nm Hz, THz, nm [100, 2000] 1457.5 nm Hz, THz, nm [100, 2000] Default value Default unit Units Value 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ 100 mW W, mW, dBm [0,+INF[ range Center frequency for pump 2 Frequency[3] Center frequency for pump 3 Frequency[4] Center frequency for pump 4 Frequency[5] Center frequency for pump 5 Frequency[6] Center frequency for pump 6 Frequency[7] Center frequency for pump 7 Power Name and description Power[0] range Output power for pump 0 Power[1] Output power for pump 1 Power[2] Output power for pump 2 Power[3] Output power for pump 3 Power[4] Output power for pump 4 Power[5] Output power for pump 5 Power[6] Output power for pump 6 Power[7] Output power for pump 7 110 PUMP LASER ARRAY Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Name and description Default value Units Value range Enabled True — True, False Iterations — [1, 1e+009] Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Determines whether or not the component is enabled Iterations Number of times to repeat the calculation 111 PUMP LASER ARRAY Notes: 112 CONTROLLED PUMP LASER Controlled Pump Laser This component is a pump laser that can be controlled by an electrical analog signal. It allows the design and simulation of automatic gain control schemes for optical amplifiers, such as control loops for the pump laser current. Ports Name and description Port type Signal type Input Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 980 nm Hz, THz, nm [0,+INF[ 20 mA — [0,+INF[ 0.5 W/A — [0,+INF[ 300 mA — [0,1000] 0 deg — ]-INF,+INF[ Emission frequency Threshold current Lasing begins and optical output sharply rises when current supplied exceeds the threshold current Slope efficiency The increase in optical output power divided by the increase in electrical input current Maximum current If the input current is above this value the output power is constant Initial phase Laser initial phase 113 CONTROLLED PUMP LASER Control Name and description Default value Units Value range Gain 1 — ]-INF,+INF[ 0 — ]-INF,+INF[ Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Name and description Default value Units Value range Enabled True — True, False Parameterized — True, False The electrical signal is multiplied by this parameter before the laser stage Bias The electrical signal is biased by this parameter before the laser stage Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Determines whether or not the component is enabled Parameterized Determines whether the output signal is parameterized or not Technical background The controlled pump laser designed for analog control of the output pump power. The input signal is first scaled by the parameters Gain and Bias. If the value of the scaled signal is less than the Maximum input current and greater than the Threshold current the current is multiplied by the Slope efficiency. The model supports individual samples for time driven simulation 114 CW LASER ARRAY CW Laser Array This component is an array of CW lasers. Ports Name and description Port type Signal type Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default Unit Value range Number of output ports 8 — [1, 1000] Linewidth 10 MHz [0, 1e+009[ Initial phase 0 deg [-1e+100,1e+100] 115 CW LASER ARRAY Frequency Name and description Frequency[0] Units Value Default value Default unit 193.1 THz Hz, THz, nm [30, 300000] 193.2 THz Hz, THz, nm [30, 300000] 193.3 THz Hz, THz, nm [30, 300000] 193.4 THz Hz, THz, nm [30, 300000] 193.5 THz Hz, THz, nm [30, 300000] 193.6 THz Hz, THz, nm [30, 300000] 193.7 THz Hz, THz, nm [30, 300000] 193.8 THz Hz, THz, nm [30, 300000] Default value Default unit Units Value 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ range Center frequency for laser 0 Frequency[1] Center frequency for laser 1 Frequency[2] Center frequency for laser 2 Frequency[3] Center frequency for laser 3 Frequency[4] Center frequency for laser 4 Frequency[5] Center frequency for laser 5 Frequency[6] Center frequency for laser 6 Frequency[7] Center frequency for laser 7 Power Name and description Power[0] range Output power for laser 0 Power[1] Output power for laser 1 Power[2] Output power for laser 2 Power[3] Output power for laser 3 Power[4] Output power for laser 4 Power[5] Output power for laser 5 116 CW LASER ARRAY Name and description Default unit 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Power[6] Units Value Default value range Output power for laser 6 Power[7] Output power for laser 7 Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — — Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Name and description Default value Default unit Units Value range Noise bandwidth 0 THz Hz, THz, nm [0,+INF[ –100 dB — ]-INF,+INF[ 3 dB — ]-INF,+INF[ Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Noise Bandwidth to create noise bins Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 117 CW LASER ARRAY Random numbers Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 118 CW LASER ARRAY ES CW Laser Array ES This component is an array of CW lasers. The emission frequencies are equally spaced (ES). Ports Name and description Port type Signal type Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default Unit Value range Number of output ports 8 — [1, 1000] Frequency 193.1 THz, Hz, nm [30,+INF[ 100 GHz, THZ, Hz, nm ]-INF,+INF[ Linewidth 10 MHz [0, 1e+009[ Initial phase 0 deg [-1e+100,1e+100] Emission frequency of the first laser Frequency spacing Frequency spacing between adjacent lasers 119 CW LASER ARRAY ES Power Name and description Default unit 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ 0 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] Power[0] Units Value Default value range Output power for laser 0 Power[1] Output power for laser 1 Power[2] Output power for laser 2 Power[3] Output power for laser 3 Power[4] Output power for laser 4 Power[5] Output power for laser 5 Power[6] Output power for laser 6 Power[7] Output power for laser 7 Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization 120 CW LASER ARRAY ES Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — — Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Name and description Default value Default unit Units Value range Noise bandwidth 0 THz Hz, THz, nm [0,+INF[ –100 dB — ]-INF,+INF[ 3 dB — ]-INF,+INF[ Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Noise Bandwidth to create noise bins Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The CW Laser Array ES is equivalent to the conventional CW Laser Array component. However, The CW Laser Array ES model is easier to set up for WDM systems, because it only requires the initial laser emission frequency and the spacing. The signal output power is the same for all the output signals. 121 CW LASER ARRAY ES Notes: 122 CW LASER MEASURED CW Laser Measured Generates a continuous wave (CW) optical signal based on measurements. You can enter parameters such as linewidth, side mode suppression, and relative intensity noise (RIN). Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz,THz, nm [0,+INF[ Power 0 dBm W, mW, dBm ]-INF,+INF[ Linewidth 10 MHz — [0,+INF[ Initial phase 0 deg — ]-INF,+INF[ Emission frequency 123 CW LASER MEASURED Side Mode Name and description Default value Default unit Units Value range Calculate side mode False — — — 1 — — [1, 100000] 75 GHz Hz, GHz, THz, nm [0,+INF[ 30 dB — [0,+INF[ False — — — Name and description Default value Default unit Units Value range RIN –130 dB/Hz — ]-INF,+INF[ False — — True, False 10 dBm W. mW, dBm ]-INF,+INF[ Determines if the signal output will have one side mode Number of side modes Number of side modes if running as a Fabry-Perot laser. Separation Mode frequency separation from the laser center frequency Suppression ratio Attenuation of the side mode relative to the output power Independent side mode When enabled, the side mode has an independent power value that can change the total average power RIN Relative intensity noise value Include RIN Determines if the RIN will be added to the output signal Measured power Value of the power during the measurement of RIN 124 CW LASER MEASURED Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] None — None, Polarization X, Polarization Y Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Polarization filter Determines the polarization of the filter Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — — Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Name and description Default value Default unit Units Value range Noise bandwidth 1 THz Hz, THz, nm [1e-100, 1e100] 100 GHz Hz, GHz, THz, nm [1, 1000] Convert noise bins — — [0, 0] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Noise Bandwidth to increase noise bins Noise bins spacing Determines noise bins spacing Convert noise bins Determines if the generated noise bins are incorporated into the signal 125 CW LASER MEASURED Random numbers Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 126 CW LASER MEASURED Technical background This model is similar to the CW Laser — however, it includes additional effects, such as multiple side modes and RIN. If the you enable the parameter Calculate side mode, the side mode will be generated according to: E out ( t ) = jϕ P [ 1 + s cos ( 2πΔf t ) + s cos ( – 2πΔf t )e ] where P is laser output power, s is the parameter Suppression ratio in linear scale, and Δ f is defined by the parameter Separation. If the parameter Independent side mode is enabled, the average signal power will be greater than P, since it includes the contribution from the side mode. If this parameter is disabled, the output power will be P. This means that the signal will be scaled in order to give the same average power. The signal phase and polarization is calculated in the same way as the CW laser. The model can also works as a Fabry-Perot laser; in this case, the parameter Number of side modes defines the number of modes of the laser. The normalized power for each mode is calculated based on the power of the central mode and the power of the first side mode [1], according to: 1 P n = -----------------------------------------2 1 n ⎛ ⎞ ⎛ ⎞ 1 + ----- – 1 ----⎝P ⎠ ⎝ M⎠ s M is the parameter Number of side modes, n is the index of each side mode pair, and P s is calculated from the power of the first side mode: where 1 P s = ---------------------------------⎛ 1--- – 1⎞ M 2 + 1 ⎝s ⎠ If the parameter Include RIN is enabled, the model generates noise bins with bandwidth and spacing that you define. The parameter RIN is the ratio of the meansquare optical intensity noise to the square of the average power [2][3]: 2 ⟨ ΔP ⟩ RIN = ---------------dB ⁄ Hz 2 Pm 2 where ⟨ ΔP ⟩ is the mean-square optical intensity fluctuation at a specific frequency 2 2 and P m is the parameter Measured power. This models estimates ⟨ ΔP ⟩ based on the parameters RIN and Measured power. The signal phase and polarization is calculated in the same way as the CW laser, where the laser phase noise is modeled using a Gaussian random variable for the 127 CW LASER MEASURED phase difference between two successive time instants with zero mean and a variance equal to 2π Δf , where Δf is the laser Linewidth. The probability density function is: Δϕ 2 -----------------1 - ⋅ e – 4πΔfdt f ( Δϕ ) = --------------------2π Δfdt where Δϕ is the phase difference between two successive time instants and dt is the time discretization. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛ 1 – k⎞ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference Azimuth α and Ellipticity ε : θ are calculated from the parameters k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) References: [1] Agrawal, G.P. and Dutta, N.K., “Semiconductor Laser”, 2nd Edition, Van Nostrand Reinhold, New York, N.Y., (1993). [2] Lau, K. Y. and Yariv, A., "Ultra-High Speed Semiconductor Laser", J. Quant. Elect., 21, 121-136, (1985). [3] Agrawal, G.P., Fiber-Optic Communication Systems, Second edition. John Wiley & Sons, Inc., N.Y., (1997). 128 DIRECTLY MODULATED LASER MEASURED Directly Modulated Laser Measured Directly modulated laser that allows you to specify the dynamic of the laser based on measured parameters. You can also enter parameters such as linewidth, chirp, side mode, suppression and relative intensity noise (RIN). Ports Name and description Port type Signal type Modulation Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz,THz, nm [0,+INF[ Digital — — Digital, Analog 10 dBm W, mW, dBm ]-INF,+INF[ 10 dB — [0,+INF[ 20 mA — [0,+INF[ Emission frequency Configuration Defines whether the laser will work in analog or digital configuration Power Laser output power Extinction ratio Steady state power ratio between marks and spaces Threshold current Lasing begins and optical output sharply rises when current supplied exceeds the threshold current 129 DIRECTLY MODULATED LASER MEASURED Name and description Default value Default unit Units Value range Slope efficiency 0.4 W/A — [0,+INF[ Linewidth 10 MHz — [0,+INF[ Initial phase 0 deg — ]-INF,+INF[ The increase in optical output power divided by the increase in electrical input current Measurements Name and description Default value Default unit Units Value range Overshoot 30 % — [0,+INF[ 30 % — [0,+INF[ 1/(Bit rate) * 0.05 s s, ms, ns, ps [0,+INF[ 1/(Bit rate) * 0.05 s s, ms, ns, ps [0,+INF[ 1/(Bit rate) * 0.5 s s, ms, ns, ps [0,+INF[ 1/(Bit rate) * 0.5 s s, ms, ns, ps [0,+INF[ (Bit rate) * 5 Hz Hz, MHz, GHz, THz [0,+INF[ (Bit rate) * 5 Hz Hz, MHz, GHz, THz [0,+INF[ Percentage of overshoot during the transition from 0 to 1 relative to the steady state power Undershoot Percentage of undershoot during the transition from 0 to 1 relative to the steady state power Rise time Defined as the time from when the rising edges reaches 0% of the amplitude to the time it reaches 100% of the amplitude Fall time Defined as the time from when the falling edges reaches 100% of the amplitude to the time it reaches 0% of the amplitude Damping time leading edge Relaxation time when the signal overshoot reaches 1/e of the max value during the transition from 0 to 1 Damping time trailing edge Relaxation time when the signal undershoot reaches 1/e of the min value during the transition from 1 to 0 Resonant frequency leading edge Frequency of the oscillations in the transition from 0 to 1 Resonant frequency trailing edge Frequency of the oscillations in the transition from 1 to 0 130 DIRECTLY MODULATED LASER MEASURED Side Mode Name and description Default value Default unit Units Value range Calculate side mode False — — True, False 1 — — [1, 100000] 75 GHz Hz, GHz, THz, nm [0,+INF[ 30 dB — [0,+INF[ Name and description Default value Default unit Units Value range RIN –130 dB/Hz — ]-INF,+INF[ False — — — 10 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Default unit Value range Alpha parameter 0 — [-100, 100] Adiabatic chirp 0 1/(W.s) ]-INF,+INF[ Determines if the signal output will have one side mode Number of side modes Number of side modes if running as a Fabry-Perot laser. Separation Mode frequency separation from the laser center frequency Suppression ratio Attenuation of the side mode relative to the output power RIN Relative intensity noise value Include RIN Determines if the RIN will be added to the output signal Measured power Value of the power during the measurement of RIN Chirp Results from changes in the steady state carrier densities 131 DIRECTLY MODULATED LASER MEASURED Polarization Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] None — None, Polarization X, Polarization Y Name and description Default value Units Value range Enabled True — True, False Parameterized — [1,+INF[ Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Polarization filter Determines the polarization of the filter Simulation Determines whether or not the component is enabled Parameterized Noise Name and description Default value Default unit Units Value range Noise bandwidth 1 THz Hz, THz, nm [1e-100, 1e100] 100 GHz Hz, GHz, THz, nm [1, 1000] Convert noise bins — — [0, 0] Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Bandwidth to increase noise bins Noise bins spacing Determines noise bins spacing Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 132 DIRECTLY MODULATED LASER MEASURED Technical background This model is a different from the Laser Measured, where you can enter measured parameters and the model calculates the rate equation parameter by using sophisticated optimization routines. Here you can enter measured parameters that describe the laser dynamics by building the laser output signal. If the parameter Configuration is Digital, the range of the amplitude of the signal input is normalized between 0 and 1. This means that this model converts the input signal to a sequence of squared pulses. The parameter Power is the steady state value of the output power at the 1 level. The steady-state value for the power at the 0 level is calculated from the parameter Extinction ratio: Er = 10 log ( P 1 ⁄ P 0 ) where P1 is the parameter Power, Er is the parameter Extinction ratio, and P0 is the steady-state power at the 0 level. The measured parameters will be used to build P(t) (see Figure 1). Figure 1 Measured parameters used to build P(t) 133 DIRECTLY MODULATED LASER MEASURED If you enable the parameter Calculate side mode, the side mode is generated according to: E out ( t ) = jϕ P ( t ) [ 1 + s cos ( 2πΔ f t ) + s cos ( – 2πΔ f t )e ] where P is laser output power, s is the parameter Suppression ratio in linear scale, and Δf is defined by the parameter Separation. The model can also works as a Fabry-Perot laser; in this case, the parameter Number of side modes defines the number of modes of the laser. The normalized power for each mode is calculated based on the power of the central mode and the power of the first side mode [1], according to: 1 P n = -----------------------------------------1 n⎞2 ⎛ ⎞ ⎛ 1 + ⎝ ----- – 1⎠ ⎝ -----⎠ Ps M M is the parameter Number of side modes, n is the index of each side mode pair, and P s is calculated from the power of the first side mode: where 1 P s = ---------------------------------⎛ 1--- – 1⎞ M 2 + 1 ⎝s ⎠ If the parameter Configuration is Analog, the model will use the parameters Threshold current and Slope efficiency to scale the input signal, without normalization.Different from the Digital, the Analog configuration supports individual samples for time driven simulation. If the parameter Include RIN is enabled, the model will generate noise bins with bandwidth and spacing that you define. The parameter RIN is the ratio of the meansquare optical intensity noise to the square of the average power [2][3]: 2 ⟨ ΔP ⟩-dB ⁄ Hz RIN = -------------2 Pm 2 where ⟨ ΔP ⟩ is the mean-square optical intensity fluctuation at a specific frequency 2 and P m is the parameter Measured power. 2 This model estimates ⟨ ΔP ⟩ based on the parameters RIN and Measured power. 134 DIRECTLY MODULATED LASER MEASURED The chirp is modeled using: α d dϕ ------ = -----e- ----- InP ( t ) + κP ( t ) 2 dt dt where ϕ is the signal phase, α e is the parameter Alpha parameter or linewidth enhancement factor, and κ is the parameter Adiabatic chirp. The signal phase and polarization is calculated in the same way as the CW laser, where the laser phase noise is modeled using a Gaussian random variable for the phase difference between two successive time instants with zero mean and a variance equal to 2π Δf , where Δf is the laser Linewidth. The probability density function is: Δϕ 2 -----------------1 - ⋅ e – 4πΔfdt f ( Δϕ ) = --------------------2π Δfdt where Δϕ is the phase difference between two successive time instants and dt is the time discretization. The output is multiplied with a complex vector considering the state of polarization: ⎛ E X ( t )⎞ = ⎛ 1 – k⎞ ⋅ P ( t ) ⎝ E ( t )⎠ ⎝ ke jθ ⎠ Y The power splitting k and the phase difference Azimuth α and Ellipticity ε : θ is calculated from the parameters k ( 1 – k ) cos ( θ -) tan ( 2α ) = 2 ---------------------------------------1 – 2.k sin ( 2ε ) = 2 k ( 1 – k ) sin ( θ ) References: [1] Agrawal, G.P. and Dutta, N.K., “Semiconductor Laser”, 2nd Edition, Van Nostrand Reinhold, New York, N.Y., (1993). [2] Lau, K. Y. and Yariv, A., "Ultra-High Speed Semiconductor Laser", J. Quant. Elect., 21, 121-136, (1985). [3] Agrawal, G.P., Fiber-Optic Communication Systems, Second edition. John Wiley & Sons, Inc., N.Y., (1997). 135 DIRECTLY MODULATED LASER MEASURED Notes: 136 VCSEL LASER VCSEL Laser This component is a vertical-cavity surface emitting laser (VCSEL). It includes thermal effects and parameter fitting based on measured LI and IV curves. Ports Name and description Port type Signal type Input Input Electrical Output Output Optical Parameters Main Name and description Default value Default unit Unit Value range Frequency 193.1 THz Hz, THz, nm [30, 3e5] 38 mA [0, 1000] 28 mA [0, 1000] Laser emission frequency Bias current Input bias current Modulation peak current Input modulation peak current Thermal Name and description Default value Thermal effects True Units Value range [True, False] Defines whether thermal effects are included in the calculation Temperature 20 C, K [-INF, +INF] 2600 C/W [0, +INF] The ambient temperature Thermal impedance Related to the temperature changes to the power dissipated as heat 137 VCSEL LASER Name and description Default value Units Value range Thermal time constant 1e-6 s [0, +INF] Name and description Default value Units Value range Reduce parameters True Response time of the device temperature Physical [True, False] Defines if the user can enter a reduced number of physical parameters Active layer volume 1.5e-010 cm3 [0, 1e-3] Group velocity 8.5e+009 cm/s [0, 100e9] Quantum efficiency 0.4 Differential gain coefficient 2.5e-016 cm2 [0, 50e-16] Carrier density at transparency 1e+018 cm-3 [0, 100e18] Mode confinement factor 0.4 Scaling factor 2.6e-008 W [0, +INF] 16000 1/s [0, +INF] [0, 1] [0, 1] Factor accounting for the output coupling efficiency Gain coefficient Coefficient in 1/s Carrier number at transparency 19400000 Carrier lifetime 1e-009 s [0, 50e-9] Photon lifetime 3e-012 s [0, 50e-9] Spontaneous emission factor 3e-005 Gain compression coefficient 1e-017 Linewidth enhancement factor 5 [-20, 20] Injection efficiency 1 [0, +INF] [0, +INF] [2e-5, 20e-5] cm3 [0.5e-17, 10e-17] Current injection efficiency Meaurements Name and description Default value Units Value range Max input current 40 mA [0, +INF] The maximum value for the signal input current. It should match the maximum value of the measurements 138 VCSEL LASER Name and description Default value Units Value range a- Ioff(T) 1.246e-3 - a0=A, [-INF, +INF] Coefficients for the polynomial function of temperature for the offset current curve 2.545e-5 a1=A/C, 2.908e-7 - a2=A/C2, 2.531e-10 a3=A/C3… 1.022e-12 b- V(T) 1 Coefficients for the polynomial function of temperature for the current-voltage curve b0=V1/2, [-INF, +INF] b1 = V 1/2 /C, b2 = V 1/2 /C2, b3= V1/2/C3… c- V(I) Coefficients for the polynomial function of current for the current-voltage curve 1.721 275 - c0=V1/2, 1/2 2.439e4 c1= V 1.338e6 - c2= V1/2/A2, 4.154e7 c3= V1/2/A3… [-INF, +INF] /A, 6.683e8 4.296e9 Parameter fitting True [True, False] Defines if the component will fit the parameters using the measurements LI curves filename The filename with the measurements of the LI curves, including the temperature dependence IV curves filename The filename with the measurements of the IV curves, including the temperature dependence LI curves at different temperatures (ACW) LI Temperature.dat IV Temperature.dat 183x3 array The values loaded from the LI curves filename IV curves at different temperatures (ACV) The values loaded from the IV curves filename 78x3 array Col 1: A Col 1: [0,+INF] Col 2: C Col 2: [-INF,+INF] Col 3: W Col 3: [0,+INF] Col 1: A Col 1: [0,+INF] Col 2: C Col 2: [-INF,+INF] Col 3: V Col 3: [0,+INF] 139 VCSEL LASER Numerical Name and description Default value Units Value range Adaptive step False — True, False 1000000 — [1e3,10e6] 0.0001 — — Defines whether to use adaptive step or not Max. number of steps The maximum number of steps Relative error Relative integration error Graphs Name and description Default value Units Value range Calculate graphs False True, False 20 [5, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 0 mA [0, +INF] 40 mA [0, +INF] Current lower limit for the graphs To Current upper limit for the graphs Simulation Name and description Default value Enabled True Parameterized Parameterized Units Value range [True, False] Noise Name and description Default value Include noise True [True, False] Include phase noise True [True, False] 140 Units Value range VCSEL LASER Random numbers Name and description Default value Units Value range Generate random seed True [True, False] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 141 VCSEL LASER Graphs Name and description X Title Y Title IV curve Current (A) Voltage (V) LI curve Current (A) Power (W) Measured IV curve Current (A) Voltage (V) Measured LI curve Current (A) Power (W) Results Name and description Units Output power W Voltage V Thermal impedance C/W Active layer volume cm^3 Quantum efficiency Gain coefficient 1/s Scaling factor W Carrier number at transparency Current at max. voltage A a0 A a1 A/C a2 A/C^2 a3 A/C^3 a4 A/C^4 a5 A/C^5 a6 A/C^6 a7 A/C^7 a8 A/C^8 a9 A/C^9 b0 V^.5 b1 V^.5/C b2 V^.5/C^2 142 VCSEL LASER Name and description Units b3 V^.5/C^3 b4 V^.5/C^4 b5 V^.5/C^5 b6 V^.5/C^6 b7 V^.5/C^7 b8 V^.5/C^8 b9 V^.5/C^9 c0 V^.5 c1 V^.5/A c2 V^.5/A^2 c3 V^.5/A^3 c4 V^.5/A^4 c5 V^.5/A^5 c6 V^.5/A^6 c7 V^.5/A^7 c8 V^.5/A^8 c9 V^.5/A^9 Technical Background The modulation dynamics of the laser are modeled by coupled rate equations that describe the relationship between the carrier density N(t), photon density S(t), and between the optical phase Φ ( t ) and temperature T(t)[1][2]. η i ( I ( t ) – I off ( t ) ) N ( t ) dN ( t )- = -----------------------------------1 ------------- – ---------- – g0 ⋅ ( N ( t ) – N t ) ⋅ ------------------------------ ⋅ S ( t ) (1) dt q⋅V τn (1 + ε ⋅ S(t)) dS ( t )- = Γ ⋅ g ⋅ ( N ( t ) – N ) ⋅ -----------------------------1 (t) + Γ ⋅ β ⋅ N ( t )- (2) ------------ ⋅ S ( t ) – S--------------------------------0 t dt (1 + ε ⋅ S(t)) τp τn dφ ( t )- = 1--- ⋅ α ⋅ Γ ⋅ g ⋅ ( Nt – N ) – ---1- (3) -----------0 t dt 2 τp dT ( t -) = ----1- ( T + ( IV (I,T) – P )R – T ) (4) -----------0 th dt τ th 0 143 VCSEL LASER where g 0 is the gain slope constant, g 0 = v g × a 0 , a 0 is the active layer gain coefficient v g is the group velocity ε is the gain compression factor N t is the carrier density at transparency β is the fraction of spontaneous emission coupled into the lasing mode Γ is the mode confinement factor V is the active layer volume τ p is the photon lifetime τ n is the electron lifetime α is the linewidth enhancement factor η i is the injection efficiency T 0 is the ambient temperature P O is the output power R th is the thermal impedance τ th is the thermal time constant The time variations for the optical and laser chips are given by [1] S ⋅ V ⋅ η0 ⋅ h ⋅ v - (5) P 0 = ----------------------------------2 ⋅ Γτ p 1 - ⋅ ----dφ- (6) Δv = --------2 ⋅ π dt where η o is the differential quantum efficiency v is the optical frequency h is Planck’s constant 144 VCSEL LASER By enabling the parameter Reduce parameters, the user can enter the alternative parameters that will be used to calculate N t , η o and a o according to: N N t = -----0- (7) V G0 V a 0 = ---------(8) vg 2kτ η o = ----------p- (9) hv where N o is the carrier number at transparency G 0 is the gain coefficient k is the scaling factor, with P O = kSV The offset current is given by a polynomial function of temperature [2]. 2 3 4 5 6 7 8 I off ( T ) = a 0 + a 1 T + a 2 T + a3 T + a 4 T + a 5 T + a6 T + a 7 T + a 8 T + a 9 T where the coefficients 9 a 0 to a 9 are given by the parameter a – Ioff ( T ) . The current-voltage (IV) relationship is modeled using a polynomial function of temperature and current [2]: · 9 9 V (T,I) = ( b 0 + b 1 T + … + b 9 T ) ⋅ ( c 0 + c 1 I + … + c 9 I ) where · 9 ( b0 + b 1 T + … + b9 T ) is · 5 2 3 4 6 7 8 9 ( b0 + b 1 T + b 2 T + b3 T + b 4 T + b 5 T + b 6 T + b7 T + b 8 T + b 9 T ) 9 ( c 0 + c 1 I + … + c 9 I ) is 2 3 4 5 6 7 8 9 ( c0 + c1 I + c2 I + c3 I + c4 I + c5 I + c6 I + c7 I + c8 I + c9 I ) where the coefficients and c – V ( I ) . b 0 to b 9 and c 0 to c 9 are given by the parameter b – V ( T ) When the parameter Parameter fitting is disabled, the component will calculate using user-defined parameters. In this case, the user should provide all the parameters, including the coefficient for the polynomial functions. The measured LI and IV curves will not be used in the calculation. 145 VCSEL LASER When the parameter Parameter fitting is enabled, the component will calculate new parameters using the current parameters as a first guess, including the number and the initial values for the polynomial coefficients. The new parameters can be seen in the component results. First the component will calculate the coefficients for the IV curve, and then it will calculate the coefficients for the offset current, the thermal impedance and the new slope efficiency. The maximum value of the input current is calculated from the current derivative of the IV curve. However, the user should provide this value as an input parameter. The parameters will be adjusted to reflect the new slope efficiency. The affected parameters are the active layer volume and the quantum efficiency. For each calculation, the component will also generate the peak power and voltage results based on the bias and modulation peak current. These values can be used for external parameter fitting if the user intends to use a different fitting engine. The file format for the LI curve data is the following: Current0 Temperature0 Power0 Current1 Temperature1 Power1 Current2 Temperature2 Power2 The units are ampere, Celsius and watt. The file format for the IV curve data is the following: Current0 Temperature0 Voltage0 Current1 Temperature1 Voltage 1 Current2 Temperature2 Voltage 2 The units are ampere, Celsius and volt. The range for the current value should be the same for both files. If the range is not the same, the parameter-fitting engine will not converge to an optimum fitting. For example, if the LI curve is provided from 0 to 40 mA, the IV curve must be also provided from 0 to 40 mA. The default parameters of the VCSEL are the same as in [2]. If the parameter Thermal effects is disabled, the calculation will perform using the same equations as in [1], without the thermal effects and the parameter fitting. Parameters Bias current and Modulation peak current are scale factors applied to the input electrical signal. 146 VCSEL LASER The internal current I ( t ) is given by: I ( t ) = I DC + I in ( t ) × I Pk (4) Where I in ( t ) is the input signal current, I DC is the parameter Bias Current and I Pk is the parameter Modulation peak current. If parameter Bias Current and Modulation peak current have zero values, the internal current is given by I in ( t ) only. The VCSEL Laser supports individual samples for time-driven simulation. References [1] J. C. Cartledge and G. S. Burley, "The Effect of the Laser Chirping on Lightwave System Performance", J. Lightwave Technology, vol. 7, pp. 568-573, March 1989. [2] P. V. Mena, J. J. Morikuni, S. M. Kang, A. V. Harton and K. W. Wyatt, "A Simple Rate-EquationBased Thermal VCSEL Model", J. Lightwave Technology, vol. 17, pp. 865-872, May 1999. 147 VCSEL LASER Notes: 148 SPATIAL CW LASER Spatial CW Laser This component is CW laser that includes transverse mode profiles in the optical output. It is a subsystem built using the CW Laser and the Multimode Generator. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THZ, nm [10, 10000] 0 dBm W, mW, dBm [-1000, 1000] 10 MHz [0, 1e+009] 0 deg [-1E+100, 1E+100] Name and description Default value Default unit Azimuth 0 deg [-90, 90] 0 deg [-45, 45] Emission frequency Power Output power Linewidth Laser linewidth Initial phase Defines the initial phase of the output signal Polarization Units Value range Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization 149 SPATIAL CW LASER Spatial effects Name and description Default value Power ratio array 1 Default unit Units Value range List of power values which describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES [YES, NO] Iterations [1, 1e+009] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for polarization Simulation Units Value range Determines whether or not the component is enabled Iterations Number of times to repeat the calculation 150 SPATIAL CW LASER Name and description Default value Default unit Units Value range Sample rate Sample rate Hz Hz, GHz, THz [1, 1e+100] Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Frequency simulation window Space width X Horizontal spatial simulation window Space width Y Vertical spatial simulation window Random Numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The layout of the Spatial CW Laser is presented in Figure 1. Refer to CW Laser and Multimode Generator component documentation for the technical background of the models. Figure 1 Spatial CW Laser subsystem 151 SPATIAL CW LASER Notes: 152 SPATIOTEMPORAL VCSEL Spatiotemporal VCSEL This component is VCSEL laser model based on 2D spatially-dependent rate equations that account dynamically for the spatial interactions between the optical field and carrier distributions in the active layer. Ports Name and description Port type Signal type Supported Modes Modulation Input Electrical Sample signals Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THZ, nm [10, 10000] 5 mA [0, 1000] 10 mA [0, 1000] Laser emission frequency Bias current Input bias current Modulation peak current Input modulation peak current 153 SPATIOTEMPORAL VCSEL Thermal Name and description Default value Thermal effects NO Default unit Units Value range [YES, NO] Define whether thermal effects are included in the calculation Temperature 300 K K, C [-1000, 1000] The ambient temperature Diode voltage 2600 Thermal impedance 3000 K/W K/W, C/W [0, 1e+100] Thermal capacitance 9.053e-012 J/K J/K, J/C [0, 1e+100] Coefficient of emission wavelength 0.06 nm/K nm/K ,nm/C [0, 1e+100] Gain peak wavelength 848 nm Reference temperature 250 K K, C [-1000, 1000] Coefficient of gain peak wavelength 0.27 nm/K nm/K, nm/C [0, 1e+100] Gain profile FWHM 40 nm [0, 1e+100] Reference leakage current 0.0006 A [0, 1e+100] Leakage current coefficients -700 5.4e-17 2.4e-19 -3.4e21 S [-1e+100, 1e+100] 154 [0, 1e+100] [0, 1e+100] SPATIOTEMPORAL VCSEL Geometrical Name and description Default value Default unit Units Value range Cavity length 9e-005 cm [0, 1e+100] Single QW thickness 0.008 um [0, 1e+100] Number of quantum wells 3 SCH thickness 0.04 um [0, 1e+100] Cavity radius 8 um [0, 1e+100] Oxide aperture radius 2.25 um [0, 1e+100] Core radius 2.25 um [0, 1e+100] Core refractive index 3.6 Refractive index change 0.6944 % Name and description Default value Default unit Group velocity 7137915666.667 cm/s [0, 1e+100] Gain coefficient 1500 1/cm [0, 1e+100] Carrier number at transparency 1.85e+018 [0, 1e+100] Optical confinement factor 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03 [0, 1] Carrier lifetime 2.5e-009 s [0, 1e+100] Gain compression coefficient 3e-017 cm^3 [1e-050, 1 Linewidth enhancement factor 2 [-1e+100, 1e+100] Top mirror reflectivity for cosine modes 0.997, 0.997, 0.997, 0.997, 0.997, 0.997, 0.997 [0, 1] Top mirror reflectivity for sine modes 0.997, 0.997, 0.997, 0.997, 0.997, 0.997, 0.997 [0, 1] Bottom mirror reflectivity for cosine modes 0.9985, 0.9985, 0.9985, 0.9985, 0.9985, 0.9985, 0.9985 [0, 1] Bottom mirror reflectivity for sine modes 0.9985, 0.9985, 0.9985, 0.9985, 0.9985, 0.9985, 0.9985 [0, 1] [0, 1e+06] [0, 1e+100] [0, 1e+100] Physical Units Value range 155 SPATIOTEMPORAL VCSEL Name and description Default value Default unit Units Value range Internal loss for cosine modes 40, 40, 40, 40, 40, 40, 40 1/cm [0, 1e+100] Internal loss for sine modes 40, 40, 40, 40, 40, 40, 40 1/cm [0, 1e+100] Thermionic emission lifetime 5e-010 s [0, 1e+100] Ambipolar diffusion time 2.5e-011 s [0, 1e+100] Current spreading coefficient 0.0001 cm [0, 1e+100] Ambipolar diffusion coefficient 12 cm^2 [0, 1e+100] Injection efficiency 1 [0, 1] Current injection efficiency Enhanced Name and description Default value Parasitic effects NO Current source resistance 1 Ohm Ohm, kOhm, MOhm [0, 1e+100] Current source capacitance 0.5 pF F, tF, pF, nF [0, 1e+100] Bond wire resistance 0.4 Ohm Ohm, kOhm, MOhm [0, 1e+100] Bond wire inductance 1 nH H, nH, uH, mH [0, 1e+100] Pad source capacitance 0.5 pF F, tF, pF, nF [0, 1e+100] Bragg reflector resistance 20 Ohm Ohm, kOhm, MOhm [0, 1e+100] Cavity resistance 30 Ohm Ohm, kOhm, MOhm [0, 1e+100] Cavity capacitance 0.5 pF F, tF, pF, nF [0, 1e+100] Feedback effects NO External cavity length 30 External power reflectance 0.03496595941 156 Default unit Units Value range [YES, NO] [YES, NO] cm [0, 1e+100] [0, 1] SPATIOTEMPORAL VCSEL Numerical Name and description Default value Units Value range Minimum time step 1e-012 s [1e-100, 1] 7 — [4, 1e+10] 1e-014 — [1e-100, 0.1] 9 — [1, 28] 4e-009 s [0, 1] If this value is lower than the sampling period, the signal is resampled using the minimum time step as the new sampling period. Radial steps Resolution along the radial direction (finite differences parameter) Mode solver tolerance The LP mode solver error tolerance Maximum number of modes The upper limit for the number of modes to be used in the calculation Time to reach steady state User estimation of the time required to reach steady-state. Steadystate values are used to initialize the internal state of the model before calculation starts. Graphs Name and description Default value Default unit Units Value range Calculate graphs NO [YES, NO] 20 [5, 1e+008] Define whether to calculate graphs or not Number of points Number of points for the graphs From 0 mA [0, 1e+100] 40 mA [0, 1e+100] Name and description Default value Default unit Enabled YES [YES, NO] Parameterized [YES, NO] Lower limit value for the graphs To Upper limit value for the graphs Simulation Units Value range Determines whether or not the component is enabled Parameterized Determines whether or not the signal output is parameterized 157 SPATIOTEMPORAL VCSEL Name and description Default value Default unit Units Value range Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Name and description Default value Default unit Include noise YES Horizontal spatial simulation window Space width Y Vertical spatial simulation window Noise Units Value range [YES, NO] Defines whether RIN will be included in the signal Random Numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description X Title Y Title LI curve Current (A) Power (W) Technical Background This module simulates a spatiotemporal model of a VCSEL and is based on the publications of Jungo et al [1][2][3][4]. It is an improved version, since it includes an LP mode solver and parameters to control whether temperature, parasitic and feedback effects are included in the calculation or not. Parameters Bias current and Modulation peak current are scale factors applied to the input electrical signal. The internal current 158 I ( t ) is given by: SPATIOTEMPORAL VCSEL I ( t ) = I DC + I in ( t ) × I Pk (3) Where I in ( t ) is the input signal current, I DC is the parameter Bias Current and I Pk is the parameter Modulation peak current. If parameter Bias Current and Modulation peak current have zero values, the internal current is given by I in ( t ) only. Due to the complexity of this component, we only give the list of parameters. For further information about the spatiotemporal model refer to the work of Jungo [1], where the exact mathematical derivation and formulation of the core model as well as of the advanced mechanisms can be found. References [1] Jungo, M., "Spatiotemporal VCSEL Model for Advanced Simulations of Optical Links,"in Series in Quantum Electronics, vol. 30, edited by H. Baltes, P. Günter, U. Keller, F. K. Kneubühl, W. Lukosz, H. Mechior, and M. W. Sigrist, 1st ed.Konstanz: Hartung-Gorre Verlag, 2003 [2] Jungo, M.X.; Erni, D.; Bachtold, W., "VISTAS: a comprehensive system-oriented spatiotemporal VCSEL model", IEEE Journal of Selected Topics in Quantum Electronics, pp. 939 - 948. Volume 9, Issue 3, May-June 2003 [3] G. Sialm, D. Lenz, D. Erni, G. -L. Bona, C. Kromer, M. X. Jungo, T. Morf, F. Ellinger, and H. Jäckel, "Comparison of Simulation and Measurement of Dynamic Fiber-Coupling Effects for High-Speed Multimode VCSELs," J. Lightwave Technol. 23, 2318- (2005) [4] M. Jungo; D. Erni; W. Baechtold, "-D VCSEL model for investigation of dynamic fiber coupling and spatially filtered noise”, IEEE Photonics Technology Letters, pp. 3 - 5, Volume 15, Issue 1, Jan. 2003 159 SPATIOTEMPORAL VCSEL Notes: 160 SPATIAL VCSEL Spatial VCSEL This component is VCSEL laser that includes transverse mode profiles in the optical output. It is a subsystem built using the VCSEL laser and the Multimode Generator. Ports Name and description Port type Signal type Supported Modes Modulation Input Electrical Sample signals Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THZ, nm [10, 10000] Bias current 5 mA [0, 1000] Modulation peak current 10 mA [0, 1000] Name and description Default value Default unit Thermal effects YES Emission frequency Thermal Units Value range [YES, NO] Define whether thermal effects are included in the calculation Temperature 20 C 2600 C/W C, K [-1000, 1000] The ambient temperature Thermal impedance [0, 1e+100] Related to the temperature changes to the power dissipated as heat 161 SPATIAL VCSEL Name and description Default value Default unit Units Value range Thermal time constant 1e-006 S Name and description Default value Default unit Reduce parameters YES Active layer volume 1e-011 cm^3 [[0, 0.001] Group velocity 8.5e+009 cm/s [0, 1e+011] Quantum efficiency 0.4 Diffential gain coefficient 2.5e-016 cm^2 [0, 5e-015] Carrier density at transparency 1e+018 cm^3 [0, 1e+020 Mode confinement factor 1 Scaling factor 2.6e-008 W [0, 1e+100] Gain coefficient 16000 1/s [0, 1e+100] Carrier number at transparency 1.94e+007 Carrier lifetime 5e-009 s [0, 5e-008] Photon lifetime 2.28e-012 s [0, 5e-008] Spontaneous emission factor 1e-006 Gain compression coefficient 1e-017 Linewidth enhancement factor 5 [-20, 20] Injection efficiency 1 [0, 1] [0, 1e+100] Response time of the device temperature Physical Units Value range [YES, NO] [0, 1] [0, 1] [0, 1e+100] [1e-100, 1] cm^3 [1e-050, 1 Current injection efficiency Measurements Name and description Default value Default unit Max input current 40 mA The maximum value for the signal input current, it should match the maximum value of the measurements 162 Units Value range [0, 1e+100] SPATIAL VCSEL Name and description Default value a - Ioff(T) 1.246e-3 Coefficients for the polynomial function of temperature for the offset current curve -2.545e-5 Default unit Units Value range 2.908e-7 -2.531e-10 1.022e-12 b - V(T) 1 Coefficients for the polynomial function of temperature for the current-voltage curve c - V(I) 1.721 275 Coefficients for the polynomial function of current for the current-voltage curve -2.439e4 1.338e6 -4.154e7 6.683e8 -4.296e9 Parameter fitting YES [YES, NO] Defines whether the component will fit the parameters using the measurements LI curves filename The filename with the measurements of the LI curves, including the temperature dependence IV curves filename The filename with the measurements of the IV curves, including the temperature dependence LI Temperature.dat IV Temperature.dat LI curves at different temperatures (A C W) The values loaded from the LI curves filename IV curves at different temperatures (A C V) The values loaded from the IV curves filename 163 SPATIAL VCSEL Spatial Effects Name and description Default value Power ratio array 1 Default unit Units Value range List of power values which describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for polarization 164 SPATIAL VCSEL Numerical Name and description Default value Units Value range Adaptive step False — True, False 1000000 — [1e3,10e6] 0.0001 — — Defines whether to use adaptive step or not Max. number of steps The maximum number of steps Relative error Relative integration error Graphs Name and description Default value Default unit Units Value range Calculate graphs NO [YES, NO] 20 [5, 1e+008] Define whether to calculate graphs or not Number of points Number of points for the graphs From 0 mA [0, 1e+100] 40 mA [0, 1e+100] Name and description Default value Default unit Enabled YES Lower limit value for the graphs To Upper limit value for the graphs Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window 165 SPATIAL VCSEL Noise Name and description Default value Default unit Units Value range Include noise YES [YES, NO] YES [YES, NO] Defines whether RIN will be included in the signal Include phase noise Defines whether the laser linewidth will be affected by the noise Random Numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description X Title Y Title LI curve Current (A) Power (W) IV curve Current (A) Voltage (V) Measure LI curve Current (A) Power (W) Measured IV curve Current (A) Voltage (V) Results Name and description Output power (W) Voltage (V) Thermal impedance (C/W) Active layer volume (cm^3) Quantum efficiency Scaling factor (W) Gain coefficient (1/s) 166 SPATIAL VCSEL Name and description Carrier number at transparency Current at max. voltage (A) a0 (A) a1 (A/C) a2 (A/C^2) a3 (A/C^3) a4 (A/C^4 a5 (A/C^5) a6 (A/C^6) a7 (A/C^7) a8 (A/C^8) a9 (A/C^9) b0 (V^0.5) b1 (V^0.5/C) b2 (V^0.5/C^2) b3 (V^0.5/C^3) b4 (V^0.5/C^4) b5 (V^0.5/C^5) b6 (V^0.5/C^6) b7 (V^0.5/C^7) b8 (V^0.5/C^8) b9 (V^0.5/C^9) c0 (V^0.5) c1 (V^0.5/A) c2 (V^0.5/A^2) c3 (V^0.5/A^3) c4 (V^0.5/A^4) c5 (V^0.5/A^5) c6 (V^0.5/A^6) c7 (V^0.5/A^7) c8 (V^0.5/A^8) 167 SPATIAL VCSEL Name and description c9 (V^0.5/A^9) Technical Background The layout of the Spatial VCSEL is presented in Figure 1. Refer to VCSEL Laser and Multimode Generator component documentation for the technical background of the models. Figure 1 168 Spatial VCSEL subsystem SPATIAL LASER RATE EQUATIONS Spatial Laser Rate Equations This component is laser based on rate equations that includes transverse mode profiles in the optical output. It is a subsystem built using the Laser Rate Equations component and the Multimode Generator. Ports Name and description Port type Signal type Supported Modes Modulation Input Electrical Sample signals, Individual samples Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [10,10000] True — — True, False 10 dBm W, mW, dBm [-1e100, 1e100] 0 dBm W, mW, dBm [-1e100, 1e100] 38 mA — [0, 1000] 23 mA — [0, 1000] Emission frequency of the laser Calculate current Defines whether to estimate the input bias and peak current to achieve the user defined steady Power Steady state power at the peak current Power at bias current Steady state power at the bias current Bias current Input bias current Modulation peak current Input modulation peak current 169 SPATIAL LASER RATE EQUATIONS Name and description Default value Default unit Units Value range Threshold current 33.4572 mA — [0, 1000] 0.02841 mW — [0, 1000] Name and description Default value Default unit Units Value range Active layer volume 1.5e-010 cm^3 Quantum efficiency 0.4 [0, 1] Spontaneous emission factor 3e-005 [2e-005, 0.0002] Gain compression coefficient 1e-017 cm^3 [5e-018, 1e-016] Carrier density at transparency 1e+018 cm^-3 [0, 1e+020] Diffential gain coefficient 2.5e-016 cm^2 [0, 5e-015] Group velocity 8.5e+009 cm/s [0, 1e+011] Linewidth enhancement factor 5 [-20, 20] Mode confinement factor 0.4 [0, 1] Carrier lifetime 1e-009 s [0, 5e-008] Photon lifetime 3e-012 s [0, 5e-008] Name and description Default value Default unit Power ratio array 1 The threshold current, calculated from the laser physical parameters Threshold power The threshold power, calculated from the laser physical parameters Physical [0, 0.001] Spatial effects Units Value range List of power values that describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization Defines how the spatial modes are attached to the output signal 170 LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y SPATIAL LASER RATE EQUATIONS Name and description Default value Pol. X LP index array 00 Default unit Units Value range List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Numerical Name and description Default value Units Value range Adaptive step False — True, False 1000000 — [1e3,10e6] 0.0001 — — Defines whether to use adaptive step or not Max. number of steps The maximum number of steps Relative error Relative integration error Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Horizontal spatial simulation window 171 SPATIAL LASER RATE EQUATIONS Name and description Default value Default unit Units Value range Space width Y Space width Y um Name and description Default value Default unit Include noise YES [YES, NO] YES [YES, NO] [1e-100, 1e+100] Vertical spatial simulation window Noise Units Value range Defines whether RIN will be included in the signal Include phase noise Defines whether the laser linewidth will be affected by the noise Random Numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The layout of the Spatial Laser Rate Equations is presented in Figure 1. Refer to Laser Rate Equations and Multimode Generator component documentation for the technical background of the models. Figure 1 172 Spatial Laser Rate Equations subsystem SPATIAL LED Spatial LED This component is an LED that includes transverse mode profiles in the optical output. It is a subsystem built using the LED component and the Multimode Generator. Ports Name and description Port type Signal type Supported Modes Modulation Input Electrical Sample signals Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [10, 10000] Electron lifetime 1e-009 s [0, 1] RC constant 1e-009 s [0, 1] Quantum efficiency 0.05 Bandwidth 6 THz Hz, THz, nm [0, 1e+100] Name and description Default value Default unit Units Value range Power ratio array 1 Emission frequency [0, 1] Spatial Effects List of power values that describe the power distribution between multiple modes 173 SPATIAL LED Name and description Default value Mode type LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines the output signal mode types Mode polarization Default unit Units Defines how the spatial modes are attached to the output signal Pol. X LP index array Value range 00 List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window 174 SPATIAL LED Random numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The layout of the Spatial LED is presented in Figure 1. Refer to LED and Multimode Generator component documentation for the technical background of the models. Figure 1 Spatial LED subsystem 175 SPATIAL LED Notes: 176 WDM TRANSMITTER WDM Transmitter This component is a WDM transmitter. Ports Name and description Port type Signal type Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default Unit Value range Number of output ports 8 — [1, 1000] Frequency 193.1 THz, Hz, nm [30,+INF[ 100 GHz, THZ, Hz, nm ]-INF,+INF[ Power 0 dBm W, mW, dBm Extinction ratio 10 dB [0,1000] Linewidth 10 MHz [0, 1e+009[ Initial phase 0 deg [-1e+100,1e+100] Emission frequency of the first laser Frequency spacing Frequency spacing between adjacent lasers 177 WDM TRANSMITTER PRBS Name and description Default value Default unit Value range Bit rate Bit rate Bits/s [0, 1e+012] MBits/s GBits/s Order log(Sequence length)/log(2) — [2,30] Number of leading zeros 1 — [0,+INF[ Number of trailing zeros 1 — [0,+INF[ Name and description Default value Default unit Value range Modulation type NRZ Order of the PRBS generator Coding Off, NRZ, RZ Defines the signal modulation type Duty cycle — Order of the PRBS generator Rise time 0.05 bit [0,1] 0.05 bit [0,1] Name and description Default value Default unit Value range Transmitter type EML — EML, DML Overshoot 30 % — 30 % — Defined as the time from when the rising edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Fall time Defined as the time from when the falling edge reaches 90% of the amplitude to the time it reaches 10% of the amplitude Enhanced Percentage of overshoot during the transition from 0 to 1 relative to the steady state power Undershoot Percentage of undershoot during the transition from 0 to 1 relative to the steady state power 178 WDM TRANSMITTER Name and description Default value Default unit Value range Damping time leading edge 1/(Bit rate) * 0.5 s s, ms, ns, ps 1/(Bit rate) * 0.5 s s, ms, ns, ps (Bit rate) * 5 Hz Hz, MHz, GHz, THz (Bit rate) * 5 Hz Hz, MHz, GHz, THz Relaxation time when the signal overshoot reaches 1/e of the max value during the transition from 0 to 1 Damping time trailing edge Relaxation time when the signal undershoot reaches 1/e of the min value during the transition from 1 to 0 Resonant frequency leading edge Frequency of the oscillations in the transition from 0 to 1 Resonant frequency trailing edge Frequency of the oscillations in the transition from 1 to 0 Side Mode Name and description Default value Default unit Units Value range Calculate side mode False — — True, False 1 — — [1, 100000] 75 GHz Hz, GHz, THz, nm [0,+INF[ 30 dB — [0,+INF[ Determines if the signal output will have one side mode Number of side modes Number of side modes if running as a Fabry-Perot laser. Separation Mode frequency separation from the laser center frequency Suppression ratio Attenuation of the side mode relative to the output power 179 WDM TRANSMITTER RIN Name and description Default value Default unit Units Value range RIN –130 dB/Hz — ]-INF,+INF[ False — — — 10 dBm W, mW, dBm ]-INF,+INF[ Name and description Default value Default unit Value range Alpha parameter 0 rad/W [-1000, 1000] Adiabatic chirp 0 1/s [-1000, 1000] Name and description Default value Units Value range Azimuth 0 deg ]-90,90] 0 deg [-45,45] None — None, Polarization X, Polarization Y Relative intensity noise value Include RIN Determines if the RIN will be added to the output signal Measured power Value of the power during the measurement of RIN Chirp Results from changes in the steady state carrier densities Polarization Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Polarization filter Determines the polarization of the filter 180 WDM TRANSMITTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Iterations — — [1,+INF[ Parameterized Parameterized — — — Sample rate Sample rate Hz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise bandwidth Sample rate THz Hz, THz, nm Sample rate GHz Hz, GHz, THz, nm Convert noise bins — — Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] False — True, False Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Frequency simulation window Noise Bandwidth to increase noise bins Noise bins spacing Determines noise bins spacing Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Different each iteration Determines if the seed is automatically defined and unique for each calculation iteration 181 WDM TRANSMITTER Technical background WDM systems require multiple transmitters and different parameters for each one of them. In addition, they also require different modulation schemes and formats. By using multiple components, users can customize designs, but it is time consuming. The WDM Transmitter encapsulates different components, allowing users to select different modulation formats and schemes for multiple channels in one single component. It is a transmitter array that allows for different modulation types and schemes. The block diagram for each WDM channel transmitter is shown below. The first stage is the PRBS; the same engine used in the Pseudo-Random Bit Sequence Generator component is used in this stage. Parameters Bit rate, Order, Number of leading and trailing zeros are used in the internal Pseudo-Random Bit Sequence Generator. A different seed will be used for each bit sequence for each WDM channel. The operation and parameters of the PRBS component is described in the technical background of the Pseudo-Random Bit Sequence Generator. The second stage is the Coding/Modulation; the parameter Modulation type has three options: RZ, NRZ and Off. RZ and NRZ coding is generated by the engines of the RZ 182 WDM TRANSMITTER Pulse Generator and NRZ Pulse Generator respectively. A CW operation of the transmitter is possible by selecting Off as modulation type. The Duty cycle parameter is used when modulation type RZ is selected. The operations and parameters of the electrical pulse generators are described in the technical background of the RZ and NRZ Pulse Generators. The last stage is the optical source and modulation scheme; by using the parameter Transmitter type the user can select between a external modulated laser scheme (EML) or a directly modulated laser scheme (DML). The laser engine used in this stage is the same used in the Directly Modulated Laser Measured component. The operation and parameters of this component are described in the technical background of the Directly Modulated Laser Measured. By using 3R regenerators, it is possible to recover the original bit sequence and electrical signals for all the WDM channels: 183 WDM TRANSMITTER Notes: 184 OPTICAL TRANSMITTER Optical Transmitter The optical transmitter is a single channel version of the WDM Transmitter component. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [1, 10000] 0 dBm W, mW, dBm [-1000, 1000] 10 dB [0, 1000] 10 MHz [0, 1e+009] 0 deg [-1e+100, 1e+100] Name and description Default value Default unit Units Value range Bit rate Bit rate Bits/s Bits/s, MBits/s, GBits/s [0, 1e+012] Emission frequency Power Output power Extinction ratio Steady-state power ratio between high and low level bits Linewidth Laser linewidth Initial phase Defines the initial phase of the output signal PRBS 185 OPTICAL TRANSMITTER Name and description Default value Order log(Sequence length)/log(2) [0, 30] Number of leading zeros 1 [0, 1000] Number of trailing zeros 1 [0, 1000] Order of the PRBS Default unit Units Value range Coding Name and description Default value Modulation type NRZ Default unit Units Value range [Off, NRZ, RZ] Defines the modulation type Duty cycle 0.5 bit [0, 1] 0 bit [-1, 1] 1/(Bit rate)*0.05 s Duration of the high level bit Position The relative position of the bit Rise time s, ms, ns, ps [0, 1e+100] s, ms, ns, ps [0, 1e+100] Units Value range Defined as the time from when the rising edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Fall time 1/(Bit rate)*0.05 Defined as the time from when the falling edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Enhanced Name and description Default value Transmitter type EML Default unit EML, DML Defines whether the transmitter uses an external modulated laser (EML) or a directly modulated laser (DML) Overshoot 30 % [0, 100] 30 % [0, 100] Percentage of overshoot during the transition from low level to high level relative to the steady-state power Undershoot Percentage of undershoot during the transition from high level to low level relative to the steady-state power 186 OPTICAL TRANSMITTER Name and description Default value Default unit Units Value range Damping time leading edge 1/(Bit rate)*0.05 s s, ms, ns, ps [0, 1e+100] 1/(Bit rate)*0.05 s s, ms, ns, ps [0, 1e+100] (Bit rate)*5 Hz Hz, MHz, GHz, THz [0, 3e+015] (Bit rate)*5 Hz Hz, MHz, GHz, THz [0, 3e+015] Name and description Default value Default unit Units Value range Calculate side mode NO [YES, NO] 1 [1, 100000] Relaxation time when the signal overshoot reaches 1/e of the max. value during the transition from low level to high level Damping time trailing edge Relaxation time when the signal undershoot reaches 1/e of the max. value during the transition from high level to low level Resonant frequency leading edge Frequency of the oscillations in the transition from low level to high level Resonant frequency trailing edge Frequency of the oscillations in the transition from high level to low level Side Mode Determines if the signal output will have side modes Number of side modes Number of side modes if running as a Fabry-Perot laser Separation 75 GHz 30 dB Name and description Default value Default unit Include RIN NO Hz, GHz, THz, nm [0, 3e+012] Mode frequency separation from the laser center frequency Suppression ratio [0, 1e+009] Attenuation of the side modes relative to the output power RIN Units Value range [YES, NO] Determines if RIN will be added to the output signal 187 OPTICAL TRANSMITTER Name and description Default value Default unit Units Value range RIN -130 dB/Hz 10 dBm W, mW, dBm [-1000, 1000] Name and description Default value Default unit Units Value range Alpha parameter 0 Adiabatic chirp 0 1/(W.s) Name and description Default value Default unit Azimuth 0 deg [-90, 90] 0 deg [-45, 45] [-1e+100, 0] Determines if RIN will be added to the output signal Measured power Value of power during the measurement of RIN Chirp [-100, 100] [-1e+100, 1e+100] Results from changes in the steadystate carrier densities Polarization Units Value range Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Polarization filter None [None, Polarization X, Polarization Y] Determines the type of polarization filter Simulation Name and description Default value Default unit Units Value range Enabled YES [YES, NO] Iterations [1, 1e+009] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Frequency simulation window 188 Sample rate Hz Hz, GHz, THz [1, 1e+100] OPTICAL TRANSMITTER Name and description Default value Default unit Units Value range Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Name and description Default value Default unit Units Value range Noise bandwidth Sample rate Hz Hz, GHz, THz, nm [0, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Noise Determines the noise bandwidth Random numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Different each iteration False — True, False Determines if the seed is automatically defined and unique for each calculation iteration Technical Background Refer to WDM Transmitter for the technical background. 189 OPTICAL TRANSMITTER Notes: 190 SPATIAL OPTICAL TRANSMITTER Spatial Optical Transmitter This component is Optical transmitter that includes transverse mode profiles in the optical output. It is a subsystem built using the WDM Transmitter Optical and the Multimode Generator. Ports Name and description Port type Signal type Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 850 nm Hz, THz, nm [1, 10000] 0 dBm W, mW, dBm [-1000, 1000] 10 dB [0, 1000] 10 MHz [0, 1e+009] 0 deg [-1e+100, 1e+100] Name and description Default value Default unit Units Value range Bit rate Bit rate Bits/s Bits/s, MBits/s, GBits/s [0, 1e+012] Emission frequency Power Output power Extinction ratio Steady-state power ratio between high and low level bits Linewidth Laser linewidth Initial phase Defines the initial phase of the output signal PRBS 191 SPATIAL OPTICAL TRANSMITTER Name and description Default value Order log(Sequence length)/log(2) [0, 30] Number of leading zeros 1 [0, 1000] Number of trailing zeros 1 [0, 1000] Order of the PRBS Default unit Units Value range Coding Name and description Default value Modulation type NRZ Default unit Units Value range [Off, NRZ, RZ] Defines the modulation type Duty cycle 0.5 bit [0, 1] 0 bit [-1, 1] 1/(Bit rate)*0.05 s Duration of the high level bit Position The relative position of the bit Rise time s, ms, ns, ps [0, 1e+100] s, ms, ns, ps [0, 1e+100] Units Value range Defined as the time from when the rising edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Fall time 1/(Bit rate)*0.05 Defined as the time from when the falling edge reaches 10% of the amplitude to the time it reaches 90% of the amplitude Enhanced Name and description Default value Transmitter type EML Default unit EML, DML Defines whether the transmitter uses an external modulated laser (EML) or a directly modulated laser (DML) Overshoot 30 % [0, 100] 30 % [0, 100] Percentage of overshoot during the transition from low level to high level relative to the steady-state power Undershoot Percentage of undershoot during the transition from high level to low level relative to the steady-state power 192 SPATIAL OPTICAL TRANSMITTER Name and description Default value Default unit Units Value range Damping time leading edge 1/(Bit rate)*0.05 s s, ms, ns, ps [0, 1e+100] 1/(Bit rate)*0.05 s s, ms, ns, ps [0, 1e+100] (Bit rate)*5 Hz Hz, MHz, GHz, THz [0, 3e+015] (Bit rate)*5 Hz Hz, MHz, GHz, THz [0, 3e+015] Name and description Default value Default unit Units Value range Calculate side mode NO [YES, NO] 1 [1, 100000] Relaxation time when the signal overshoot reaches 1/e of the max. value during the transition from low level to high level Damping time trailing edge Relaxation time when the signal undershoot reaches 1/e of the max. value during the transition from high level to low level Resonant frequency leading edge Frequency of the oscillations in the transition from low level to high level Resonant frequency trailing edge Frequency of the oscillations in the transition from high level to low level Side Mode Determines if the signal output will have side modes Number of side modes Number of side modes if running as a Fabry-Perot laser Separation 75 GHz 30 dB Name and description Default value Default unit Include RIN NO Hz, GHz, THz, nm [0, 3e+012] Mode frequency separation from the laser center frequency Suppression ratio [0, 1e+009] Attenuation of the side modes relative to the output power RIN Units Value range [YES, NO] Determines if RIN will be added to the output signal 193 SPATIAL OPTICAL TRANSMITTER Name and description Default value Default unit Units Value range RIN -130 dB/Hz 10 dBm W, mW, dBm [-1000, 1000] Name and description Default value Default unit Units Value range Alpha parameter 0 Adiabatic chirp 0 1/(W.s) Name and description Default value Default unit Azimuth 0 deg [-90, 90] 0 deg [-45, 45] [-1e+100, 0] Determines if RIN will be added to the output signal Measured power Value of power during the measurement of RIN Chirp [-100, 100] [-1e+100, 1e+100] Results from changes in the steadystate carrier densities Polarization Units Value range Azimuth angle of output polarization Ellipticity Ellipticity angle of output polarization Polarization filter None [None, Polarization X, Polarization Y] Determines the type of polarization filter Spatial Effects Name and description Default value Power ratio array 1 Default unit Units Value range List of power values that describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization Defines how the spatial modes are attached to the output signal 194 LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y SPATIAL OPTICAL TRANSMITTER Name and description Default value Pol. X LP index array 00 Default unit Units Value range List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES [YES, NO] Iterations [1, 1e+009] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Simulation Units Value range Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Sample rate Sample rate Hz Hz, GHz, THz [1, 1e+100] Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Frequency simulation window Space width X Horizontal spatial simulation window Space width Y Vertical spatial simulation window 195 SPATIAL OPTICAL TRANSMITTER Noise Name and description Default value Default unit Units Value range Noise bandwidth Sample rate Hz Hz, GHz, THz, nm [0, 1e+100] Determines the noise bandwidth Random numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Different each iteration False — True, False Determines if the seed is automatically defined and unique for each calculation iteration Technical Background The layout of the Spatial Optical Transmitter is presented in Figure 1. Refer to WDM Transmitter and Multimode Generator component documentation for the Technical Background of the models. Figure 1 Spatial Optical Transmitter subsystem 196 PSEUDO-RANDOM BIT SEQUENCE GENERATOR Pseudo-Random Bit Sequence Generator Generates a Pseudo Random Binary Sequence (PRBS) according to different operation modes. The bit sequence is designed to approximate the characteristics of random data. Ports Name and description Port type Signal type Bit sequence Output Binary Parameters Main Name and description Default value Default unit Value range Bit rate Bit rate Bits/s [0, 1e+012] MBits/s GBits/s Operation mode Order — Probability, Order, Alternate, Ones, Zeros Order log(Sequence length)/log(2) — [2,30] 0.5 — [0,1] Number of leading zeros (Time window * 3 / 100 ) * Bit rate — [0,+INF[ Number of trailing zeros (Time window * 3 / 100 ) * Bit rate — [0,+INF[ Order of the PRBS generator Mark probability Probability of ones in the sequence 197 PSEUDO-RANDOM BIT SEQUENCE GENERATOR Simulation Name and description Default value Units Value range Enabled True — True, False Iterations — [1, 1e+009] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Random numbers Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] False — True, False Determines if the seed is automatically defined and unique Random seed index User-defined seed index for bit generation Different each iteration Determines if the seed is automatically defined and unique for each calculation iteration Technical background This model generates a sequence of N bits: where N = T w B r NG = N – nl – nt Tw is the global parameter Time window and Br is the parameter Bit rate. The number of bits generated is the Number of trailing zeros. N G . n l and n t are the Number of leading zeros and Operation mode controls the algorithm used to generate the bit sequence: 198 • Probability: Random number generator is used, with parameter Mark probability specifying the probability of ones in the sequence • Order: PRBS generator[1] with Order k is used to generate a sequence with period of 2k-1 • Alternate: Alternate sequence of ones and zeros is generated • Ones: A sequence of ones is generated • Zeros: A sequence of zeros is generated PSEUDO-RANDOM BIT SEQUENCE GENERATOR References [1] Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T., Numerical Recipes in C. Cambridge University Press, (1991). 199 PSEUDO-RANDOM BIT SEQUENCE GENERATOR Notes: 200 USER-DEFINED BIT SEQUENCE GENERATOR User-Defined Bit Sequence Generator Generates a bit sequence that is user-defined. Ports Name and description Port type Signal type Bit sequence Output Binary Parameters Main Name and description Default value Units Value range Bit rate Bit rate Bits/s [0,+INF[ MBits/s GBits/s Load from file False — True, False Sequence.dat — Filename 0101101110 — String Number of leading zeros (Time window * 3 / 100 ) * Bit rate — [0, 1000] Number of trailing zeros (Time window * 3 / 100 ) * Bit rate — [0, 1000] Determines whether or not the component will load the bit sequence from the file Filename File with the bit sequence Bit sequence User-defined bit sequence 201 USER-DEFINED BIT SEQUENCE GENERATOR Simulation Name and description Default value Units Value range Enabled True — True, False 1 — [1, 1e+009] Determines whether or not the component is enabled Iterations Number of times to repeat the calculation Technical background You can enter the string Bit sequence or choose Load from file. In this, case the parameter Filename is enabled. All bit files are formatted containing one bit per line, e.g. the bit file representing the sequence "01011..." has the following form: 0 1 0 1 1 The sequence length is defined by: N = TwBr Tw is the global parameter Time window and Br is the parameter Bit rate. If the userdefined sequence is shorter than the N, the sequence will be repeated until the length is equal to N. 202 MACH-ZEHNDER MODULATOR Mach-Zehnder Modulator Simulates a Mach-Zehnder modulator using an analytical model. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Extinction ratio 30 dB [0,+INF[ Negative signal chirp False — True, False Symmetry factor –1 — [-1,1[ Name and description Default value Units Value range Enabled True — True, False Simulation Determines whether or not the component is enabled Technical background The Mach-Zehnder modulator is an intensity modulator based on an interferometric principle. It consists of two 3 dB couplers which are connected by two waveguides of equal length (see Figure 1). By means of an electro-optic effect, an externally applied voltage can be used to vary the refractive indices in the waveguide branches. 203 MACH-ZEHNDER MODULATOR The different paths can lead to constructive and destructive interference at the output, depending on the applied voltage. Then the output intensity can be modulated according to the voltage. Figure 1 Mach-Zehnder modulator The equations that describe the behavior of the MZ modulator are: E out ( t ) = Ein ( t ) ⋅ cos ( Δθ ( t ) ) ⋅ exp ( j ⋅ Δφ ( t ) ) where Δθ is the phase difference between the two branches and is defined as: Δθ ( t ) = π --- ⋅ ( 0.5 – ER ⋅ ( Modulation ( t ) – 0.5 ) ) 2 with 1 ⎞ ER = 1 – --4- ⋅ arc tan ⎛⎝ ------------------π extrat⎠ and Δφ is the signal phase change defined as: Δφ ( t ) = SC ⋅ Δθ ( t ) ⋅ ( 1 + SF ) ⁄ ( 1 – SF ) where the parameter SC is –1 if negative signal chirp is true, or 1 if negative signal chirp is false. extract is the extinction ratio, SF is the symmetry factor, and modulation(t) is the electrical input signal. The electrical input signal is normalized between 0 and 1. 204 MACH-ZEHNDER MODULATOR For parameterized and noise bins signals, the average power is calculated according to the above. 205 MACH-ZEHNDER MODULATOR Notes: 206 ELECTROABSORPTION MODULATOR Electroabsorption Modulator Simulates an Electro-absorption modulator using an analytical model. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Modulation index 0.95 — [0,1[ Chirp factor 0 — ]-INF, +INF[ Name and description Default value Units Value range Enabled True — True, False Simulation Determines whether or not the component is enabled 207 ELECTROABSORPTION MODULATOR Technical background In this model, the optical carrier is modulated externally by the electrical modulation signal, (see Figure 1). Figure 1 EA modulator Assuming that the optical input signal is Ein, the following equation describes the behavior of the model: E out ( t ) = E in ( t ) ⋅ Mod ( t ) ⋅ exp ⎛⎝ j α --- ⋅ ln ( Mod ( t ) )⎞⎠ 2 where Eout(t) is the output optical signal, α is the chirp factor, and Mod(t) is defined as Mod ( t ) = ( 1 – MI ) + MI ⋅ modulation ( t ) where MI is the modulation index and modulation(t) is the electrical input signal. The electrical input signal is normalized between 0 and 1. For parameterized and noise bins signals, the average power is calculated according to the above. 208 AMPLITUDE MODULATOR Amplitude Modulator Simulates an ideal amplitude modulator. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Modulation index 1 — [0,1] Name and description Default value Units Value range Enabled Yes — True, False Simulation Determines whether or not the component is enabled 209 AMPLITUDE MODULATOR Technical background In this model, the optical carrier is modulated externally by the electrical modulation signal. Assuming that the optical input signal is Ein, the following equations describe the behavior of the model: Eout ( t ) = E in ( t ) ⋅ Mod ( t ) where Eout(t) is the output optical signal and Mod(t) is defined as Mod ( t ) = ( 1 – MI ) + MI ⋅ modulation ( t ) where MI is the modulation index and modulation(t) is the electrical input signal. The electrical input signal is normalized between 0 and 1. For parameterized and noise bins signals, the average power is calculated according to the above. 210 PHASE MODULATOR Phase Modulator Simulates an ideal phase modulator. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Normalize electrical signal True — True, False 90 deg ]-INF,+INF[ Name and description Default value Units Value range Enabled True — True, False Defines if the electrical input signal will be normalized between 0 and 1 Phase deviation Simulation Determines whether or not the component is enabled 211 PHASE MODULATOR Technical background In this model, the electrical modulation signal imposes a phase modulation on an optical carrier. Assuming that the optical input signal is Ein, the following equation describes the behavior of the model. E out ( t ) = E in ( t ) ⋅ exp ( j ⋅ Δφ ⋅ modulation ( t ) ) where Eout(t) is the output optical signal, Δφ is the phase deviation, and modulation(t) is the electrical input signal. The electrical input signal is normalized between 0 and 1. The parameterized and noise bins signals are not affected by this modulator. 212 FREQUENCY MODULATOR Frequency Modulator Simulates an ideal frequency modulator. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Unit Value range Frequency deviation 10 GHz Hz, GHz, THz [0,+INF[ Name and description Default value Units Value range Enabled True — True, False Simulation Determines whether or not the component is enabled 213 FREQUENCY MODULATOR Technical background In this model, the electrical modulation signal imposes a frequency modulation on an optical carrier. Assuming that the optical input signal is Ein, the following equation describes the behavior of the model: t ⎛ ⎞ E out ( t ) = E in ( t ) ⋅ exp ⎜ j ⋅ 2π ∫ Δf ⋅ ( modulation ( τ ) – 0.5 ) dτ⎟ ⎝ ⎠ 0 where Eout(t) is the output optical signal, Δf is the frequency deviation, and modulation ( τ ) is the electrical input signal. The electrical input signal is normalized between 0 and 1. The parameterized and noise bins signals are not affected by this modulator. 214 DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Dual Drive Mach-Zehnder Modulator Measured Simulates a Mach-Zehnder modulator with dual-drive modulation using measured parameters. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Splitting Ratio 1.3 — [0,10000] Modulator Type Phase-Shift — Conventional, Phase-Shift Bias Voltage 1 –2.8 V ]-INF, +INF[ Bias Voltage 2 –1.1 V ]-INF, +INF[ Normalize electrical signal True — True, False Modulation Voltage12 1.2 V [0, +INF[ Absorption / Phase Filename AbsorptionPhase. dat — — Name and description Default value Units Value range Enabled True — True, False File with the measured absorption and phase Simulation Determines whether or not the component is enabled 215 DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Graphs Name and description X Title Y Title Measured absorption Voltage (V) Absorption (dB) Measured phase Voltage (V) Phase (radians) Technical background In this model, you can specify the dependence of the measured absorption and phase on applied voltage for a Mach-Zehnder modulator. You can use the default characteristics curves or choose to load from Filename. For a modulator with the same input and output Y-branch splitting ratios, the output signal is: Δα a ( V 1 ) E0 Δα a ( V2 ) - SR ⋅ exp ⎛ – ⎛ --------------------E ( V1 ,V 2 ) = --------------+ j ⋅ Δβ ( V1 )⎞ L⎞ + exp ⎛ – ⎛ --------------------+ j ⋅ Δβ ( V2 )⎞ L – j ⋅ φ 0⎞ ⎝ ⎝ ⎠ ⎠ ⎝ ⎝ ⎠ ⎠ 2 2 1 + SR E ( V 1 ,V2 ) ≡ I ( V1 ,V 2 ) ⋅ exp ( j ⋅ Φ ( V 1 ,V 2 ) ) where SR = P1/P2 is the Y-branch power splitting ratio Δα a ⁄ 2 Δβ L φ0 V1 , V2 I Φ is the attenuation constant is the phase constant is the interaction length of the modulator arm is 0 radians for a conventional modulator and π radians for phase-shift modulator are voltages applied to arms 1 and 2, respectively is the intensity of the optical signal is the phase V i ( i = 1, 2 ) is defined as: V i ( t ) = V bi + V mod12 ⋅ v ( t ) for the normalized case where V bi is the bias voltage, V mod12 is the peak-to-peak voltage, and v ( t ) is the normalized modulation waveform with a peak-to-peak amplitude of 1 and an average value of 0. The electrical input signal can be normalized between 0.5 and -0.5. V i ( t ) = V bi ± V mod ( t ) for the non-normalized case. The model utilizes a Dual drive (push and pull) modulation ( ΔV 1 216 = – ΔV 2 . DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED The model has stored default curves characteristics of a Mach-Zehnder modulator. The dependence of the measured absorption and phase of the optical signal on applied voltage for each arm of a modulator is illustrated in Figure 1. Figure 1 Default characteristics of absorption and phase in the Dual Mach-Zehnder model 217 DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Reference: [1] Cartledge, J. C., “Combining self-phase modulation and optimum modulation conditions to improve performance of 10 Gb/s transmission systems using MQW Mach-Zehnder modulators”, J. Light. Techn., 18, 647-654, (2000). 218 ELECTROABSORPTION MODULATOR MEASURED Electroabsorption Modulator Measured Simulates an Electro-absorption modulator using measured parameters. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Bias voltage –1 V ]-INF, +INF[ Normalize electrical signal True — True, False Modulation voltage (peak-to-peak) 2 V [0, +INF[ Absorption / Alpha Filename AbsorptionAlpha.dat — — File with the measured absorption and α-parameter αm Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 219 ELECTROABSORPTION MODULATOR MEASURED Graphs Name and description X Title Y Title Measured absorption Voltage (V) Absorption (dB) Measured alpha-parameter Voltage (V) Alpha-parameter Calculated alpha-parameter Voltage (V) Alpha-parameter Technical background In this model, you can specify the dependence of the measured absorption and α parameter- α m on the applied voltage for an EA modulator. You can use the default characteristic curves or choose to load from file. In this case, the parameter Filename is enabled. In the case of the EA modulator, the output signal response to an applied voltage is: E(V ) = I ( V ) exp ⎛ j 1--- ∫ α m ( V ) d ln ( I ( V ) )⎞ ⎝ 2 ⎠ (1) where IV is the voltage-dependent intensity of the signal. While Equation 1 is an accurate result, it is not in the most convenient form for simulation purposes when empirical equations for α m ( V ) and I ( V ) are obtained from a fitting to measured results. The determination of the argument of the exponential function in Equation 1 requires function evaluation and integration. The modulator output signal given by Equation 1 can also be written in the convenient ( 1 + jα ) ⁄ 2 form I using a voltage-dependent parameter α r ( V ) as: E( V) = I(V ) ( 1 + jα r ( V ) ) ⁄ 2 (2) A comparison of the phase terms in Equation and Equation 2 yields 1 α r ( V ) = ----------- ∫ α m ( V ) ⋅ dγ ( V ) γ(V ) (3) Equation 3 shows how the attenuation constant γ ( V ) and α-parameter- α m ( V ) jointly combine to determine α r ( V ) . Using Equation 2, with α r ( V ) determined from measurements of α m ( V ) and I ( V ) , the evaluation of the argument of the exponent only requires function evaluation. 220 ELECTROABSORPTION MODULATOR MEASURED The default characteristics curves stored in the component, the dependence of the measured absorption, and α-parameter- α m ( V ) on applied voltage, is illustrated in Figure 1. Figure 1 Dependence of the absorption and αm on the applied voltage for an MQW-EAM For this component, the electrical input signal can be normalized between 0.5 and -0.5. Then, the voltage applied to the modulator is given by: (4) V ( t ) = V b + Vmod ⋅ v ( t ) where Vb is the bias voltage, Vmod is the peak-to-peak voltage, and v(t) is the normalized modulation waveform (electrical input signal) with a peak-to-peak amplitude of 1 and an average value of 0. 221 ELECTROABSORPTION MODULATOR MEASURED Notes: 222 SINGLE DRIVE MACH-ZEHNDER MODULATOR MEASURED Single Drive Mach-Zehnder Modulator Measured Simulates a Mach-Zehnder modulator with single drive modulation using measured parameters. Ports Name and description Port type Signal type Modulation Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Splitting Ratio 1.3 — [0,10000] Modulator Type Phase-Shift — Conventional, Phase-Shift Bias Voltage 1 –2.8 V ]-INF, +INF[ Bias Voltage 2 –1.1 V ]-INF, +INF[ Normalize electrical signal True — True, False Modulation Voltage 1.5 V [0, +INF[ Operation mode Change in V2 = 0 — Change in V1 = 0, Change in V2 = 0 Absorption / Phase Filename AbsorptionPhase.dat — — File with the measured absorption and phase 223 SINGLE DRIVE MACH-ZEHNDER MODULATOR MEASURED Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Graphs Name and description X Title Y Title Measured absorption Voltage (V) Absorption (dB) Measured phase Voltage (V) Phase (radians) Technical background In this model, you can specify the dependence of the measured absorption and phase on applied voltage for a Mach-Zehnder modulator. You can use the default characteristics curves or choose to load from Filename. For a modulator with the same input and output Y-branch splitting ratios, the output signal is: E0 Δα a ( V 1 ) Δα a ( V2 ) E ( V1 ,V 2 ) = --------------+ j ⋅ Δβ ( V1 )⎞ L⎞ + exp ⎛ – ⎛ --------------------+ j ⋅ Δβ ( V2 )⎞ L – j ⋅ φ 0⎞ - SR ⋅ exp ⎛ – ⎛ --------------------⎠ ⎠ ⎝ ⎝ ⎠ ⎠ ⎝ ⎝ 2 2 1 + SR E ( V 1 ,V2 ) ≡ I ( V1 ,V 2 ) ⋅ exp ( j ⋅ Φ ( V 1 ,V 2 ) ) where SR = P1/P2 is the Y-branch power splitting ratio Δα a ⁄ 2 Δβ L φ0 V1 , V2 I Φ is the attenuation constant is the phase constant is the interaction length of the modulator arm is 0 radians for a conventional modulator and π radians for phase-shift modulator are voltages applied to arms 1 and 2, respectively is the intensity of the optical signal is the phase Vi(i=1,2) is defined as: V i ( t ) = V bi + V modi ⋅ v ( t ) for the normalized case where Vbi is the bias voltage, Vmodi is the peak-to-peak voltage, v(t) is the normalized modulation waveform with a peak-to-peak amplitude of 1 and an average value of 0. The electrical input signal is normalized between 0.5 and -0.5. 224 SINGLE DRIVE MACH-ZEHNDER MODULATOR MEASURED V i ( t ) = V bi ± V mod ( t ) for the non-normalized case The model utilizes a single drive modulation, i.e., Vmod is 0 in one of the arms. The model has stored default curves characteristics of a Mach-Zehnder modulator. The dependence of the measured absorption and phase of the optical signal on applied voltage for each arm of a modulator is illustrated in Figure 1. Figure 1 Default characteristics of absorption and phase in the Single Mach-Zehnder mode 225 SINGLE DRIVE MACH-ZEHNDER MODULATOR MEASURED Reference: [1] Cartledge, J. C., “Combining self-phase modulation and optimum modulation conditions to improve performance of 10 Gb/s transmission systems using MQW Mach-Zehnder modulators”, J. Light. Techn., 18, 647-654, (2000). 226 DUAL PORT DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Dual Port Dual Drive Mach-Zehnder Modulator Measured Simulates a Mach-Zehnder modulator with dual-drive modulation using two ports with measured parameters. Ports Name and description Port type Signal type Modulation 1 Input Electrical Modulation 1 Input Electrical Carrier Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Splitting Ratio 1.3 — [0,10000] Modulator Type Phase-Shift — Conventional, Phase-Shift, Bias Voltage 1 –2.8 V ]-INF, +INF[ Bias Voltage 2 –1.1 V ]-INF, +INF[ Normalize electrical signal True — True, False Modulation Voltage12 1.2 V [0, +INF[ Absorption / Phase Filename AbsorptionPhase.dat — — File with the measured absorption and phase 227 DUAL PORT DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Graphs Name and description X Title Y Title Measured absorption Voltage (V) Absorption (dB) Measured phase Voltage (V) Phase (radians) Technical background In this model, you can specify the dependence of the measured absorption and phase on applied voltage for a Mach-Zehnder modulator. You can use the default characteristics curves or choose to load from Filename. For a modulator with the same input and output Y-branch splitting ratios, the output signal is: Δα a ( V 1 ) E0 Δα a ( V2 ) - SR ⋅ exp ⎛ – ⎛ --------------------E ( V1 ,V 2 ) = --------------+ j ⋅ Δβ ( V1 )⎞ L⎞ + exp ⎛ – ⎛ --------------------+ j ⋅ Δβ ( V2 )⎞ L – j ⋅ φ 0⎞ ⎠ ⎠ ⎝ ⎝ ⎠ ⎠ ⎝ ⎝ 2 2 1 + SR E ( V 1 ,V2 ) ≡ I ( V1 ,V 2 ) ⋅ exp ( j ⋅ Φ ( V 1 ,V 2 ) ) where SR = P 1 ⁄ P 2 is the Y-branch power splitting ratio Δα a ⁄ 2 Δβ L φ0 V1 , V2 I Φ is the attenuation constant is the phase constant is the interaction length of the modulator arm is 0 radians for a conventional modulator and π radians for phase-shift modulator are voltages applied to arms 1 and 2, respectively is the intensity of the optical signal is the phase V i ( i = 1, 2 ) is defined as: V i ( t ) = V bi ± V modi ⋅ v ( t ) for the normalized case where V bi is the bias voltage, V modi is the peak-to-peak voltage, and v ( t ) is the normalized modulation waveform with a peak-to-peak amplitude of 1 and an average value of 0. The electrical input signal is normalized between 0.5 and -0.5. 228 DUAL PORT DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED V i ( t ) = V bi ± V modi ( t ) for the non-normalized case. The model utilizes a Dual drive (push and pull) modulation ( ΔV 1 = – ΔV 2 . The model has stored default curves characteristics of a Mach-Zehnder modulator. The dependence of the measured absorption and phase of the optical signal on applied voltage for each arm of a modulator is illustrated in Figure 1. Figure 1 Default characteristics of absorption and phase in the Dual Mach-Zehnder model 229 DUAL PORT DUAL DRIVE MACH-ZEHNDER MODULATOR MEASURED Reference: [1] Cartledge, J. C., “Combining self-phase modulation and optimum modulation conditions to improve performance of 10 Gb/s transmission systems using MQW Mach-Zehnder modulators”, J. Light. Techn., 18, 647-654, (2000). 230 LITHIUM NIOBATE MACH-ZEHNDER MODULATOR Lithium Niobate Mach-Zehnder Modulator This component simulates a Lithium Niobate Mach-Zehnder modulator based on measured parameters. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Electrical Input 3 Input Electrical Output 1 Output Optical Parameters Main Name and description Default value Default unit Value range Extinction ratio 20 dB [0,+INF[ Switching bias voltage 4 V [0,+INF[ 4 V ]-INF,+INF[ Bias voltage1 0 V ]-INF,+INF[ Bias voltage2 4 V ]-INF,+INF[ Insertion loss 5 dB [0,+INF[ Normalize electrical signal True — True, False Modulation voltage1 0 V ]-INF,+INF[ Modulation voltage2 4 V ]-INF,+INF[ DC voltage required to turn the modulator from the OFF state to the ON state, or vice versa Switching RF voltage RF voltage required to turn the modulator from the OFF state to the ON state, or vice versa 231 LITHIUM NIOBATE MACH-ZEHNDER MODULATOR Bandwidth Response Name and description Default value Units Value range Load transfer function False — True, False Hz — Hz, THz Power — Power; Phase; Power Phase; Real, Imag. True — True, False Filter.dat — — Name and description Default value Units Value range Enabled True — True, False Determines whether you want to load a modulator transfer function or use an ideal one. File frequency unit Determines the frequency unit of the file. File format Determines the format of the file. Linear scale Determines whether or not the data is in linear scale. HF filename File with the transfer function (S21) Simulation Determines whether or not the component is enabled Technical background The Mach-Zehnder structure consists of an input optical branch, which splits the incoming light into two arms, followed by two independent optical arms, which are subsequently recombined by the output optical branch. Application of an electrical signal to one of the optical arms controls the degree of interference at the output optical branch and therefore controls the output intensity. The optical field at the output of the modulator is given by: Ein ( t ) ( j ⋅ π ⋅ v 2 ( t ) ⁄ V πRF + j ⋅ π ⋅ v bias2 ⁄ V πDC ) ( j ⋅ π ⋅ v 1 ( t ) ⁄ V πRF + j ⋅ π ⋅ v bias1 ⁄ V πDC ) E O ( t ) = --------------------------------------------⋅ (γ ⋅ e + (1 – γ) ⋅ e ) ( insertionloss ⁄ 20 ) 10 where E in ( t ) is the input signal v 1 ( t ) and v 2 ( t ) are the RF modulating electrical voltage v bias1 and v bias2 are the DC bias voltage applied to arm one and two, respectively 232 LITHIUM NIOBATE MACH-ZEHNDER MODULATOR γ denotes the power splinting (combining) ration of arm two for the input (output, respectively) Y-branch waveguide, and is given by: 1 ⎞ ⁄2 γ = ⎛⎝ 1 – -------ε⎠ r where ε r = 10 ExtRatio ⁄ 10 . v bias1 and v bias2 , the DC bias voltages, are included separately as parameters due to the possibility of the V πDC (Switching Bias Voltage) to be different from the Switching RF Voltage. If the Switching Bias Voltage is equal to the Switching RF Voltage, and the Normalize Electrical Signal parameter is False, the bias voltage can be included in the electrical signal. The optical power and phase of the modulator output are determined in response to the modulating voltage waveforms. The modulator transfer function relates the effective drive voltage to the applied drive voltage. This component can also load the modulator transfer function data from file or consider an ideal transfer function. The file is formatted containing two items per line, the frequency and filter measurement. The parameter File frequency unit determines the frequency unit of the first item; it can be Hz or THz. According to the parameter File format, the second item can be one value (Power or Phase) or two values (Power and Phase or Real and Imag): Power (Phase is set to zero, assuming frequency units THz) 193.10 0 193.11 0.5 193.12 0.5 193.13 0 Power Phase 193.14 0 0 193.15 0.5 3.14 193.16 0.5 3.14 193.17 0 0 233 LITHIUM NIOBATE MACH-ZEHNDER MODULATOR Real Imag 193.18 0 0 193.19 -0.5 7.9-e-4 193.20 -0.5 7.9-e-4 193.21 0 0 Phase (Power is set to one) 193.22 0 193.23 3.14 193.24 3.14 193.253 0 When the Normalize electrical signal parameter is True, the electrical signals of port1 and port2 are normalized between -0.5 and 0.5. In this case, the amplitude of each RF electrical signal considered in v 1 ( t ) and v 2 ( t ) will be the values in the modulation voltage parameters divided by 2. References [1] Cartledge, J. C., Rolland, C., Lemerle, S., and Solheim, A., “Theoretical performance of 10 Gb/s lightwave systems using a III-V semiconductor Mach-Zehnder modulator.”, IEEE Phot. Techn. Letters., 6, 282-284, (1994). [2] Cartledge, J.C., "Performance of 10 Gb/s lightwave systems based on lithium niobate MachZehnder modulators with asymmetric Y-branch waveguides". IEEE Phot. Techn. Letters., 7, 1090 -1092, (1995). 234 Multimode Library This section contains information on the following multimode components • Donut Transverse Mode Generator • Hermite Transverse Mode Generator • Laguerre Transverse Mode Generator • Multimode Generator • Measured Transverse Mode 235 MULTIMODE LIBRARY Notes: 236 DONUT TRANSVERSE MODE GENERATOR Donut Transverse Mode Generator This component attaches Donut transverse mode profiles to the input signal. It also converts single-mode signals into multimode signals. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Main Name and description Default value Power ratio array 1 Value range List of power values that describe the power distribution between multiple modes Mode polarization X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X L index array 0 List of mode indexes ”l” for X polarization Pol. X outer radius 5 um [1e-100, 1e+100] 0 um [0, 1e+100] Outer radius for X polarized mode Pol. X inner radius Inner radius for X polarized mode Pol. Y L index array 0 List of mode indexes “l” for Y polarization 237 DONUT TRANSVERSE MODE GENERATOR Name and description Default value Default unit Units Value range Pol. Y outer radius 5 um [1e-100, 1e+100] 0 um [0, 1e+100] Name and description Default value Default unit Enabled YES Outer radius for Y polarized mode Pol. Y inner radius Inner radius for Y polarized mode Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The Donut [1] Transverse Mode Generator attaches mode profiles to the input signal X and Y polarizations. A donut profile is attached to each polarization. Additionally, single-mode inputs can be converted to a multimode signal scaled by a user-defined power distribution. The parameter Power ratio array is used to convert a single-mode signal into a multimode signal. The size of the list is the number of signal modes, with time-domain waveforms identical except for the power ratio factor. The sum of the power values is normalized to “1” and used to scale the time-domain signals. A Power ratio parameter of “1 2 3” will generate “3” modes. Each mode will have power ratio equal to 1/6, 2/6 and 3/6, respectively. The parameter Mode polarization defines how the spatial modes are attached to the signal polarization. The user can select whether the mode profile is attached to only one polarization (X or Y), or to both polarizations. If attached to both polarizations, it can be the same for both (X=Y) or unique (X and Y). The user can provide the list of mode indexes for each polarization, as well as the inner and outer radius for the modes. 238 DONUT TRANSVERSE MODE GENERATOR The donut modes is described as: where l is the azimuthal index, rinner is the inner radius and router is the outer radius for each mode. References [1] Mahmoud, S.W.Z.; Wiedenmann, D.; Kicherer, M.; Unold, H.; Jager, R.; Michalzik, R.; Ebeling, K.J. "Spatial investigation of transverse mode turn-on dynamics in VCSELs", IEEE Photonics Technology Letters, Volume: 13, Issue: 11, Nov. 2001 Pages: 1152 - 1154. 239 DONUT TRANSVERSE MODE GENERATOR Notes: 240 HERMITE TRANSVERSE MODE GENERATOR Hermite Transverse Mode Generator This component attaches Hermite-Gaussian transverse mode profiles to the input signal. It also converts single-mode signals into multimode signals. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Main Name and description Default value Power ratio array 1 Value range List of power values which describe the power distribution between multiple modes Mode polarization X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes “l, m” for X polarization Pol. X spot size X 5 um [1e-100, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] X-axis spot size for X polarization Pol. X spot size Y Y-axis spot size for X polarization Pol. X inv. radius of curvature X X-axis inverse radius of curvature for X polarization 241 HERMITE TRANSVERSE MODE GENERATOR Name and description Default value Default unit Units Value range Pol. X inv. radius of curvature Y 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 1 um [1e-100, 1e+100] 0 1/um [0, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES Y-axis inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes “l, m” for Y polarization Pol. Y spot size X X-axis spot size for Y polarization Pol. Y spot size Y Y-axis spot size for Y polarization Pol. Y inv. radius of curvature X X-axis inverse radius of curvature for Y polarization Pol. Y inv. radius of curvature Y Y-axis inverse radius of curvature for Y polarization Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The Hermite Transverse Mode Generator attaches mode profiles to the input signal X and Y polarizations. A Hermite-Gaussian profile [1][2] is attached to each polarization. Additionally, single-mode inputs can be converted to a multimode signal scaled by a user-defined power distribution. The parameter Power ratio array is used to convert a single-mode signal into a multimode signal. The size of the list is the number of signal modes, with time-domain waveforms identical except for the power ratio factor. The sum of the power values is normalized to “1” and used to scale the time-domain signals. 242 HERMITE TRANSVERSE MODE GENERATOR A Power ratio parameter of “1 2 3” will generate “3” modes. Each mode will have power ratio equal to 1/6, 2/6 and 3/6, respectively. The parameter Mode polarization defines how the spatial modes are attached to the signal polarization. The user can select whether the mode profile is attached to only one polarization (X or Y), or to both polarizations. If attached to both polarizations, it can be the same for both (X=Y) or unique (X and Y). The user can provide the list of mode indexes for each polarization, as well as the spot size and the inverse of the radius of curvature for each mode for both X and Y-axis. The Hermite-Gaussian mode is described as: where l and m represent the X and Y index that describe the mode dependencies for the X and Y-axis. R is the radius of curvature and w0 is the spot size. Hl and Hm are the Hermite polynomials. References [1] A. E. Siegman, Lasers, University Science Books, Sausalito, CA, 1986. [2] A. Ghatak, K. Thyagarajan, Introduction to Fiber Optics, Cambridge University Press, New York, NY, 1998. 243 HERMITE TRANSVERSE MODE GENERATOR Notes: 244 LAGUERRE TRANSVERSE MODE GENERATOR Laguerre Transverse Mode Generator This component attaches Laguerre-Gaussian transverse mode profiles to the input signal. It also converts single-mode signals into multimode signals. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Main Name and description Default value Power ratio array 1 Value range List of power values which describe the power distribution between multiple modes Mode polarization X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'lm' for X polarization Pol. X spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Spot size for X polarization Pol. X inv. radius of curvature Inverse radius of curvature for X polarization 245 LAGUERRE TRANSVERSE MODE GENERATOR Name and description Default value Pol. Y LP index array 00 Default unit Units Value range List of mode indexes 'lm' for Y polarization Pol. Y spot size 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The Hermite Transverse Mode Generator attaches mode profiles to the input signal X and Y polarizations. A Hermite-Gaussian profile [1][2] is attached to each polarization. Additionally, single-mode inputs can be converted to a multimode signal scaled by a user-defined power distribution. The parameter Power ratio array is used to convert a single-mode signal into a multimode signal. The size of the list is the number of signal modes, with time-domain waveforms identical except for the power ratio factor. The sum of the power values is normalized to “1” and used to scale the time-domain signals. A Power ratio parameter of “1 2 3” will generate “3” modes, each mode will have power ratio equal to 1/6, 2/6 and 3/6, respectively. The parameter Mode polarization defines how the spatial modes are attached to the signal polarization. The user can select whether the mode profile is attached to only one polarization (X or Y), or to both polarizations. If attached to both polarizations, it can be the same for both (X=Y) or unique (X and Y). The user can provide the list of mode indexes for each polarization, as well as the spot size and the inverse of the radius of curvature for each mode. 246 LAGUERRE TRANSVERSE MODE GENERATOR The Laguerre-Gaussian mode is described as: where l and m represent the X and Y index that describe the azimuthal and radial indexes, respectively. R is the radius of curvature and w0 is the spot size. Ll,m is the Laguerre polynomial. References [1] A. E. Siegman, Lasers, University Science Books, Sausalito, CA, 1986. [2] A. Ghatak, K. Thyagarajan, “Introduction to Fiber Optics”, Cambridge University Press, New York, NY, 1998. 247 LAGUERRE TRANSVERSE MODE GENERATOR Notes: 248 MULTIMODE GENERATOR Multimode Generator This component attaches transverse mode profiles to the input signal. It also converts single-mode signals into multimode signals. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Spatial effects Name and description Default value Power ratio array 1 Value range List of power values which describe the power distribution between multiple modes Mode type Defines the output signal mode types Mode polarization LaguerreGaussian LaguerreGaussian, HermiteGaussian X=Y X = Y, X and Y, X, Y Defines how the spatial modes are attached to the output signal Pol. X LP index array 00 List of mode indexes 'l,m' for X polarization Pol. X spot size 5 um [1e-100], 1e+100] Spot size for X polarization 249 MULTIMODE GENERATOR Name and description Default value Default unit Units Value range Pol. X inv. radius of curvature 0 1/um [0, 1e+100] 5 um [1e-100, 1e+100] 0 1/um [0, 1e+100] Name and description Default value Default unit Enabled YES Inverse radius of curvature for X polarization Pol. Y LP index array 00 List of mode indexes 'l,m' for Y polarization Pol. Y spot size Spot size for Y polarization Pol. Y inv. radius of curvature Inverse radius of curvature for Y polarization Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The Multimode Generator attaches mode profiles to the input signal X and Y polarizations. A Hermite-Gaussian or a Laguerre-Gaussian profile [1][2] is attached to each polarization. Additionally, single-mode inputs can be converted to a multimode signal scaled by a user-defined power distribution. The parameter Power ratio array is used to convert a single-mode signal into a multimode signal. The size of the list is the number of signal modes, with time-domain waveforms identical except for the power ratio factor. The sum of the power values is normalized to “1” and used to scale the time-domain signals. A Power ratio parameter of “1 2 3” will generate “3” modes, each mode will have power ratio equal to 1/6, 2/6 and 3/6, respectively. The parameter Mode polarization defines how the spatial modes are attached to the signal polarization. The user can select whether the mode profile is attached to only one polarization (X or Y), or to both polarizations. If attached to both polarizations, it can be the same for both (X=Y) or unique (X and Y). 250 MULTIMODE GENERATOR The user can provide the list of mode indexes for each polarization, as well as the spot size and the inverse of the radius of curvature for each mode. Refer to the Laguerre Transverse Mode Generator component for the analytical representation of the Laguerre-Gaussian profile. For the Hermite-Gaussian profile, the Multimode Generator assumes the same values for the spot size and radius of curvature for the X and Y-axis. Refer to the Hermite Transverse Mode Generator component for the analytical representation of the Hermite-Gaussian profile. References [1] A. E. Siegman, “Lasers”, University Science Books, Sausalito, CA, 1986. [2] A. Ghatak, K. Thyagarajan, “Introduction to Fiber Optics”, Cambridge University Press, New York, NY, 1998. 251 MULTIMODE GENERATOR Notes: 252 MEASURED TRANSVERSE MODE Measured Transverse Mode This component attaches measured transverse mode profiles to the input signal. The measured profiles are loaded from a file using the BCF3DCX format. It also converts single-mode signals into multimode signals Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Spatial effects Name and description Default value Power ratio array 1 Value range List of power values which describe the power distribution between multiple modes Mode polarization X=Y Defines how the spatial modes are attached to the output signal Pol. X files X = Y, X and Y, X, Y ““ List of files for X polarization Pol. Y files ““ List of files for Y polarization 253 MEASURED TRANSVERSE MODE Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NO] Determines whether or not the component is enabled Space width X Space width X um [1e-100, 1e+100] Space width Y um [1e-100, 1e+100] Horizontal spatial simulation window Space width Y Vertical spatial simulation window Technical Background The measured transverse mode generator attaches mode profiles to the input signal X and Y polarizations. A transverse mesh from a file is attached to each polarization, additionally; single-mode inputs can be converted to a multimode signal scaled by a user defined power distribution. The parameter Power ratio array is used to convert a single-mode signal into a multimode signal. The size of the list is the number of signal modes, with time-domain waveforms identical except for the power ratio factor. The sum of the power values is normalized to “1” and used to scale the time-domain signals. A Power ratio parameter of “1 2 3” will generate “3” modes, each mode will have power ratio equal to 1/6, 2/6 and 3/6, respectively. The parameter Mode polarization defines how the spatial modes are attached to the signal polarization. The user can select whether the mode profile is attached to only one polarization (X or Y), or to both polarizations. If attached to both polarizations, it can be the same for both (X=Y) or unique (X and Y). The user can provide the list of filed for each polarization using the parameters Pol. X files and Pol. Y files. For each power ratio a filename must be provided. Different from other OptiSystem components, the measured transverse mode generator will reload the files every time it calculates. This means the files must exist or an error message will be generated during loading. A Power ratio parameter of '1 2 3' will generate '3' modes and the parameter Pol. X files should have three lines; each line will have the file name of a mode. For example: Mode_X_1_1.f3d Mode_X_2_1.f3d Mode_X_3_1.f3d The files should have the complex data file format BCF3DCX. Files that follow this format are generated from the Save Transverse Mode component from OptiSystem or the output files in BPM 3D. 254 MEASURED TRANSVERSE MODE Complex Data 3D File Format: BCF3DCX This format applies to input and output files that contain complex data as text. The file contains the file header, number of x and y data points, mesh widths in x and y, and the complex z (x,y) data points. The data points are presented in one column with the order determined by scanning the x and y coordinates. BCF3DCX - file header NX NY - number of x and y data points WX WY - mesh widths in x and y Z1 - complex number z data point with coordinates (xmin, ymin) Z2 - complex number z data point with coordinates (xmin+dx, ymin) Z3 - complex number z data point with coordinates (xmin+2dx, ymin) . . . ZNX - complex number z data point with coordinates (xmax, ymin) ZNX+1 - complex number z data point with coordinates (xmin, ymin+dy) . . . ZN - last complex number z data point with coordinates (xmax, ymax), N=NXxNY where dx = (xmax-xmin)/(nx-1) and dy = (ymax-ymin)/(ny-1). 255 MEASURED TRANSVERSE MODE Example: Complex field (end of propagation) in BPM 3D [*.f3d] In this example, the number of data points is 100 and equals to the number of mesh points. The transverse mesh extends from -5.000000E+000 to 5.000000E+000 microns giving the mesh width 1.000000E+001 microns. BCF3DCX 100 100 1.000000E+001 1.100000E+001 -4.582487025358980E-004, -2.411965546811583E-002 1.813879122411751E-004, -2.322439514101689E-002 8.864140535377826E-004, -2.245463661588051E-002 . . . -1.004141897700716E-002, 7.709994296904761E-003 -9.736326254112302E-003, 8.732395427319460E-003 -9.270032367315658E-003, 9.686774052240091E-003 256 Optical Fibers Library This section contains information on the following optical fibers. • Optical fiber • Optical fiber CWDM • Bidirectional Optical Fiber • Nonlinear Dispersive Fiber (Obsolete) • Linear Multimode Fiber • Parabolic-Index Multimode Fiber • Measured-Index Multimode Fiber 257 OPTICAL FIBERS LIBRARY Notes: 258 OPTICAL FIBER Optical fiber The optical fiber component simulates the propagation of an optical field in a singlemode fiber with the dispersive and nonlinear effects taken into account by a direct numerical integration of the modified nonlinear Schrödinger (NLS) equation (when the scalar case is considered) and a system of two, coupled NLS equations when the polarization state of the signal is arbitrary. The optical sampled signals reside in a single frequency band, hence the name total field [1]. The parameterized signals and noise bins are only attenuated. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Symbol Default value Default unit Value range TRUE — TRUE/FALSE λ0 1550 nm [100, 2000] L 50 km [0, 100,000] — TRUE — TRUE/FALSE User defined reference wavelength If TRUE, frequency value of “Reference wavelength” is used internally as ‘zero’ (or reference) frequency in spectrum of signal envelope. Values of parameters (attenuation, dispersion) are assumed to correspond to this frequency. If parameters are wavelengthdependent (from files), they are evaluated at this frequency. If FALSE, central frequency of simulated band is used. Reference wavelength Value of user defined/specified reference wavelength. Length Fiber length Attenuation effect If TRUE, attenuation effect is enabled. 259 OPTICAL FIBER Name and description Symbol Default value Default unit Value range Attenuation data type — Constant — Constant/ From File α 0.2 dB/km [0, 1010] — — — — Defines the attenuation as a fixed constant value or as a wavelength dependent curve taken from a file. If ‘constant’, value from “Attenuation” tab in component is used. Attenuation Specified value is used if “Attenuation data type” is set to ‘constant’. If ‘from file’, the value is ignored. Attenuation vs. wavelength Defines the attenuation as a wavelength dependent curve in a file. Dispersion Name and description Symbol Default value Default unit Value range Group velocity dispersion — TRUE — TRUE/FALSE — TRUE — TRUE/FALSE Constant — Constant/ From File β2 -20 ps2/km [-10100, 10100] β3 -20 ps3/km [-10100, 10100] D 16.75 — [-10100, 10100] If TRUE, the GVD effect is enabled. Third order dispersion If TRUE, the TOD effect is enabled. Frequency domain parameters Defines domain in which dispersion parameters are specified. If TRUE, frequency domain is used and dispersion effect is specified in terms of β 2 and β 3 . Otherwise, wavelength domain is used ( D and S ). Dispersion data type Defines if dispersion parameter values are read from component tabs, or taken from a file Beta 2 Value of the GVD parameter in the frequency domain Beta 3 Value of the GVD parameter in the frequency domain Dispersion ps ------------------------( nm ) ( km ) Value of the GVD parameter in the wavelength domain Dispersion slope Value of dispersion slope parameter. 260 — [-10100, 10100] 0.075 ps --------------------------2 ( nm ) ( km ) OPTICAL FIBER Name and description Symbol Default value Default unit Value range Dispersion file format — Dispersion vs wavelengtht — Dispersion vs wavelength/ Group delay vs wavelength — — — — Determines contents of dispersion file: group delay or dispersion vs. wavelength. If “Dispersion vs. wavelength” and “Frequency domain parameters” are selected, it is assumed that file contains β 2 ( λ ) . If “Frequency domain parameters” is disabled, component assumes that file contains D ( λ ) . If “Group delay vs wavelength”, the file contains β1 ( λ ) . Dispersion file name Specifies file containing dispersion data The parameter “Frequency domain parameters” refers to the alternative definitions: ∂β D = --------1-, S = ∂D ------- (wavelength domain definition) ∂λ ∂λ and ∂β ∂β β 2 = --------1-, β 3 = --------2- (frequency domain definition) ∂ω ∂ω of the dispersion parameters, but not to the argument of these functions, which is always assumed to be the wavelength. All the parameters in the component β 2 and β 3 ) are given as functions of wavelength (not frequency). This is also the case when β 1 or β 2 are specified from a file - the first column of the file contains wavelength values ( λ ) and the second column - the corresponding values of β 1 ( λ ) or β 2 ( λ ) . (including PMD Name and description Symbol Default value Default unit Value range Birefringence type — Deterministic — Deterministic/ Stochastic d - ( Δβ ) -----dω 0.2 ps-----km [-10100, 10100] Defines the birefringence. If “Deterministic”, both the strength of birefringence and principal axes are assumed constant, hence random mode coupling is disabled. If “Stochastic”, random mode coupling is enabled. Differential group delay If Birefringence type is “Deterministic”, this is the value of the differential group delay. If “Stochastic”, parameter is disabled. 261 OPTICAL FIBER Name and description Symbol Default value Default unit Value range PMD coefficient Dp 0.5 ps ---------km [0,10100] L scatt 500 m [0,10100] σ scatt 100 m [0,10100] Polarization mode dispersion coefficient. If Birefringence type is “Stochastic”, this is the value of the PMD parameter. If “Deterministic”, parameter is disabled. Mean scattering section length Averaged value of fiber length at which the polarization state of the signal is randomized by applying the scattering matrix. Scattering section dispersion Dispersion of the scattering section length. Nonlinearities Name and description Symbol Default value Default unit Value range Self-phase modulation — TRUE — TRUE/FALSE Constant — Constant/ From File Determines if the self-phase modulation (SPM) effect will be taken into account. If FALSE all the nonlinear effects self-steepening, SRS - are disabled. In the vector case enabling this effect enables also the cross-phase modulation between the orthogonal polarization components. Effective area data type Defines is effective area parameter value is read from the component tab or from a file. If “Constant”, the value from the component is used. Effective area Defines the value of the effective area parameter. This value is used if “Effective area data type” is set to “Constant”. Otherwise, the value is ignored. Effective area vs. wavelength [0,1010] A eff 80 — — — — — Constant — Constant/ From File n2 2.6 X 10-20 μm 2 If “Effective area data type” is “From file”, this tab specifies the file containing the effective area data. n2 data type Determines if n 2 parameter (nonlinear index of refraction) value is read from the component tab or from a file. If “Constant”, value is taken from component. n2 The value of the n 2 parameter (nonlinear index of refraction). If data type is set to “Constant”, this value is used, otherwise the value is ignored. 262 2 m -----W [0,10100] OPTICAL FIBER Name and description Symbol Default value Default unit Value range Self-steepening — FALSE — FALSE/TRUE — FALSE — FALSE/TRUE — FALSE — FALSE/TRUE τ R1 14.2 fs [0,10100] τ R2 3 fs [0,10100] ρ 0.18 — [0, 1] αf 0.75 — [0, 1] Specifies whether self-steepening effect is taken into account. Can be enabled only after enabling the SPM, and is taken into account only in the scalar case (if Model type is set to Scalar), and if Full Raman response parameter is FALSE. Full Raman response Defines the stimulated Raman scattering (SRS) effect representation in the model. If TRUE, SRS is represented through the convolution integrals of the fields with the Raman susceptibilities [6, 18-21]. Intrapulse Raman scattering is disabled. Intrapulse Raman scattering Defines the stimulated Raman scattering (SRS) for [1921]. Can be enabled if Full Raman response is FALSE. If both Full Raman response and Intrapulse Raman scattering are FALSE, SRS effect is not taken into account in the simulation. Raman self-shift time 1 Value of the Raman self-shift time parameter associated with the parallel SRS effect t τR1 = ( dImχ 1111 ( ω ) ⁄ dω ) ω = 0 Units are such that Re ( χ 1111 ( ω = 0 ) ) = 1 [19-21]. Raman self-shift time 2 τ R2 = ( dImχ 1122 ( ω ) ⁄ dω ) ω = 0 Units are such that Re ( χ 1111 ( ω = 0 ) ) = 1 [18, 20, 21]. Fractional Raman contribution Fraction of the nonlinear polarization, related to the stimulated Raman scattering effect [2]. Orthogonal Raman factor α f = Re ( χ 1122 ( ω = 0 ) ) Units are such that Re ( χ 1111 ( ω = 0 ) ) = 1 . 263 OPTICAL FIBER Numerical Name and description Symbol Default value Default unit Value range Model type — Scalar — Scalar/Vect or Exponential — Exponential RungeKutta 4th order Defines model type used for simulation. Depends on polarization state of signal. If “Vector” selected, signal can have arbitrary polarization state and a system of two coupled equations (17) is solved. If “Scalar” selected, the signal preserves its polarization state and a single equation is solved (1). In the following cases, vector simulation is performed regardless of value of model type parameter: • • Two polarization components are detected at fiber input PMD effect is “Stochastic”. Propagator type Method used to apply nonlinear propagator in the split-step Fourier method. “Exponential” corresponds to standard implementation [2], “Runge-Kutta 4th (2nd) order” uses Runge-Kutta 4th (2nd) order (see [3]) to apply nonlinearity operator. Exponential cannot be used when Model type is set to Vector, and SRS effect is enabled. The default selection is Runge-Kutta 2nd order. Calculation type Exponential RungeKutta 2nd order — Iterative — Iterative/ Noniterative 2 — [2, 1010] Variable — Variable/ Constant 3.14 mrad [0,10100] Specifies implementation of split-step Fourier method [2, 4] when Propagator type is “Exponential”. Number of iterations Switch On/Off the dispersion slope (the third-order dispersion) Step Size — Specifies whether variable or fixed step-size simulation is used. If “Variable”, step size is adaptively changed depending on value of “Max. nonlinear phase shift” parameter, and solution itself. If “Constant”, step size is evaluated once at the beginning of simulation. In some cases, the fixed step size calculation executes faster, due to the smaller number of calculations per step, but the variable step size calculation is more flexible and can be faster if the peak power of the waveform varies considerably in z (for example, in the presence of strong attenuation). Max. Nonlinear phase shift Maximum (over the time window) phase shift induced by the self-phase modulation effect per step. 264 NL ϕ max OPTICAL FIBER Name and description Symbol Default value Default unit Value range Boundary conditions — Periodic — Periodic/ Absorbing — 0.5 — [0,10100] — [1400, 1700] nm [100, 2000] Specifies type of boundary conditions used in simulation. Filter steepness If “Boundary conditions” option is set to “Absorbing”, the “Filter steepness” parameter determines the absorption/reflection properties of the time window boundaries. Lower/Upper calculation limit Set the spectral range in which the simulation is performed. Any spectral components outside the range is ignored. Graphs Name and description Symbol Default value Default unit Value range Calculate graph — FALSE — FALSE/TRUE — 200 — [1, 100000000] — 200 — [1, 100000000] — TRUE — TRUE/FALSE Enables/disables 3D graphs. If disabled, no graphs are plotted and no data are stored. Number of distance steps Number of snapshots used to construct a 3D plot. If this value is increased, the fidelity of the plot is improved only if the value is below the number of actual steps in z . The number of snapshots stored cannot be bigger than the number of steps in z taken by the simulation to obtain the solution. The latter is determined by the maximum nonlinear phase-shift parameter (numerical tab). Number of wavelength/time steps Number of stored points per snapshot. If this value is increased, the fidelity of the plot is improved only if the value is below the actual number of points in the time (frequency) domain used by the simulation to obtain the solution. The latter is related to the number of samples, which is a global parameter. Linear scale Determines axis type (linear or logarithmic) for the dependent variable. If TRUE, the axis type is linear. Note: The rest of the parameters in the Graphs tab of the component determine which graphs are plotted after the simulation is complete. 265 OPTICAL FIBER Simulation Name and description Symbol Default value Default unit Value range Enabled — TRUE — TRUE/FALSE Name and description Symbol Default value Default unit Value range Convert noise bins — FALSE — FALSE/TRUE Name and description Symbol Default value Default unit Value range Generate random seed — TRUE — TRUE/FALSE — 0 — [0, 4999] Determines whether or not the component is enabled. If FALSE, all input signals reach the output port of the component without any changes. Noise If TRUE, each noise bin within the bandwidth of the signal is converted to a Gaussian white noise, with the correct power spectral density, and the noise is added to the signal. Random numbers Determines how random number generator is initialized (seeded). If TRUE, the seed index used for the initialization is the random number itself. Otherwise, a user specified number is used. Random seed index If “Generate random seed” is FALSE, this value specifies the seed index. The generated pseudorandom sequence is the same if the seed index is not changed. The value of the “Random seed index” is ignored if “Generate random seed” is TRUE. 266 OPTICAL FIBER Technical Background Scalar approach Basic equation When the optical field is assumed to maintain its polarization along the fiber length, the evolution of a slowly varying electric field envelope can be described by a single nonlinear Schrödinger (NLS) [2] equation (the scalar approach, Model type parameter from the "Numerical" tab is set to "Scalar") of the form: 2 2⎞ ⎛ 2 β3 ( ω0 ) ∂3 E 2 ∂E ∂ E i ∂ ∂ E ------ + αE + iβ 2 ( ω 0 ) --------- – ----------------- --------- = iγ ⎜ E E + ------ ------ ( E E ) – ρτ R1 E ------------⎟ 2 6 ∂T 3 ∂z ω 0 ∂T ∂T ⎠ ⎝ ∂T (1) E = E ( z, T ) is the electric field envelope. A frame moving at the group velocity ( T = t – z ⁄ v g ≡ t – β 1 z ) is assumed. In Equation 2, The derivatives of the propagation constant of the fiber mode β ( ω ) , ( ( β ( ω )c ) ⁄ ω is the mode effective index), with respect to frequency n ∂ β (ω 0 ) β n = -------------------, n = 1, 2, 3 . n ∂ω ( β 2 ) and ( β 3 ) are the first and the second group velocity dispersion (GVD) parameters, respectively, and ω 0 is the reference frequency of the signal, related to the parameter "Reference wavelength" ("Main" category of the components tool-box) through ω 0 = 2πc --------- with c being the light speed in vacuum. λ0 The physical meaning of the terms in Equation 2 is the following. The first term takes into account the slow changes of the electric field along the fiber length. The second term takes into account the linear losses of optical fiber. The third term represents the (first-order) group velocity dispersion. This is the effect responsible for the pulse broadening. (See "Group velocity dispersion" in the Tutorials). The next term is the second-order GVD, known also as third-order dispersion (TOD). This effect becomes important for a signal with a broad spectrum (e.g. femtosecond pulses or WDM systems with many channels). The pulse shape becomes asymmetric due to the effect of TOD. (See "Third order dispersion" from the Tutorials). The parameters and ( β2 ) ( β 3 ) are denoted as "frequency domain parameters" in the interface of the component (see the "Dispersion" category in the Parameters table). The following 267 OPTICAL FIBER relations are used internally to convert between them and the commonly used wavelength domain parameters D (dispersion) and S (dispersion slope). dβ 2πc- β D = --------1- = – -------2 2 dλ λ (2) λ -⎞ 2 ( λ 2 S + 2λD ), S = dD β 3 = ⎛ -------------⎝ 2πc⎠ dλ The parameter γ is given by: ω0 n2 γ = ----------cA eff (3) In Equation 3, n 2 is the nonlinear refractive index coefficient and A eff is the fiber effective area. The first term in the right-hand side in Equation 1 accounts for the selfphase modulation effect. It is responsible for the broadening of the pulse spectra and, in the presence of anomalous GVD, for the formation of optical solitons (See "Selfphase modulation" and "Self-phase modulation and group velocity dispersion" from the Tutorials). The second term in the right-hand side of Equation 1 takes into account the self-steepening effect. It leads to an asymmetry in the SPM-broadened spectra of ultrashort (femtosecond) pulses [2] and is responsible for the formation of optical shocks (see "Self-steepening" in the Tutorials). This effect will be taken into account only if the "Full Raman response" parameter is set to False. The last term in Equation 1 accounts for the intra-pulse Raman scattering effect with the parameter τ R1 being the parallel Raman self-shift time. The intra-pulse Raman scattering is an approximation to the actual Raman response of the material which is valid provided that signal spectrum is narrow compared to the Raman-gain spectrum. The τ R parameter is related to the slope of the imaginary part of the Raman susceptibility Im ( χ 1111 ( ω ) ) at zero frequency offset [2]. The parameter ρ is the fractional contribution of the delayed response of the material to the total nonlinearity [2]. The intra-pulse Raman scattering effect is responsible for the self-frequency shift i.e. energy transfer from higher to lower spectral components. It leads to a decay of higher order solitons into its constituents (see "Intrapulse Raman scattering" in the Tutorials). The intrapulse Raman scattering plays the most important role among the higher order nonlinear effects [2]. In a WDM system, the stimulated Raman scattering is responsible for an energy transfer from higher to lower frequency channels (crosstalk). The Raman induced crosstalk can be neglected when the following relation is satisfied [5]: P TOT B TOT L E < 9mWTHzMm , 268 (4) OPTICAL FIBER L E ≈ z ⁄ ( L amp α ) is the total effective length, α is the fiber loss, L amp is the amplifier spacing, z the link length, P TOT is the total optical power, and B TOT is the where total optical bandwidth. Full Raman response By selecting the option "Full Raman response" from the Numerical tab, the component can simulate the SRS effect even if the signal spectrum is much narrower than the Raman gain spectrum. In this case Equation 1 is replaced by: ∞ 2 ⎛ iβ 2 ( ω 0 )∂ E ∂ 2 E β 3 ( ω 0 ) ∂ 3 E 2 2 ⎞ E + αE + ------------------------------- --------- – ----------------- --------- = iγ ⎜ ( 1 – ρ ) E E + ρE ∫ h 1111 ( s ) E ( T – s ) ds (4a) 2 ∂z 2 6 ∂T 3 ⎝ ⎠ ∂T 0 Contained within Equation (4a) is h 1111 ( t ) which is the (time-domain) Raman response function [2], [20]. It is the Fourier-transform of the of the Raman susceptibility χ 1111 ( ω ) . In this case the self-steeping effect is neglected. Numerical solution In dimensionless form, Equation 1 reduces to: 2 3 2 2 U- + N U 2 U = iD ∂--------U- + N U -----------∂ U - – iN ---∂ i ∂U ------- + D 2 ∂--------1 3 2 3 ( U U ) – iAU , 2 3 ∂ξ ∂t ∂t ∂t ∂t (5) where the coefficients are given by: sign ( β 2 ) LD L D sign ( β 3 ) LD LD -, D 3 = ---------------------------D 2 = ---------------------, N 1 = -----, N 2 = -----τ R' , N 3 = -------- s. 2 L D' L NL L NL L NL (6) The new quantities are introduced according to: 2 LD 3 T T0 τR 1 , L ' = ------1 -, τ ' = ----= -------0-, L NL = --------, s = ----------,E = D R β2 γP0 β3 ω0 T0 To P 0 U, T = T 0 t, z = ξL D T 0 is the time window size and P 0 is the maximum (over the time 2 window) of the electric field intensity E ( z = 0, T ) . In Equation 7, 269 (7) OPTICAL FIBER The symmetrized split-step Fourier method [2, 4] is used to solve Equation 5. The ξ to ξ + h ( h is the step-size, related to the value of the NL 2 Max. nonlinear phase shift parameter ϕ max = max ( U h ) ) according to: solution is advanced from ⎛ U ( ξ + h, t ) = exp ⎛⎝ h--- D̂⎞⎠ exp ⎜ 2 ⎝ where the dispersion (ξ + h) ∫ ξ ⎞ N̂ ( ξ' ) dξ'⎟ exp ⎛ h--- D̂⎞ U ( ξ, t ) , ⎝2 ⎠ ⎠ (8) D̂ and nonlinearity N̂ operators are given by: 2 3 ∂ - + D -----∂ D̂ = iD 2 -----3 3- – A 2 ∂t ∂t (9) and 2 2 2 ∂U ∂U ∂U N̂ = iN 1 U – iN 2 ------------- – N 3 ⎛⎝ ------------- + U∗ ------- ⎞⎠ ∂t ∂t ∂t (10) The different options available from the "Numerical" tab specify the details of the implementation of Equation 8 and Equation 10 (see Figure 1). The simplest (and the fastest) implementation corresponds to "Propagator type" set to "Exponential" and "Calculation type" set to "Noniterative". In this case, the following approximation is used: ξ+h ∫ ξ 270 N̂ ( ξ' ) dz' ≈ hN̂ ( exp [ ( h ⁄ 2 )D̂ ] U ( ξ, t ) ) . (11) OPTICAL FIBER Figure 1 Component “Numerical" tab According to Equation 11, the half-step propagated field, with the nonlinear effects ignored, is used in turn to evaluate the nonlinearity operator. The dispersion operator is evaluated in the frequency domain according to: –1 Ũ D ⎛⎝ ξ + h---⎞⎠ = FFT exp ⎛⎝ h--- D̂ ( iω )⎞⎠ FFT [ U ( ξ, t ) ] , 2 2 (12) where FFT means fast Fourier transform. If, in addition the "Step size" option is set to "Constant" ("Propagator type", "Exponential", and "Calculation type" are set to "Noniterative"), the number of operations per step decreases because the first and the last Fourier transform for each step cancels each other out (dispersion operators combine) (see Equation 13). ⎛ h U ( ξ + 2h, t ) = exp ⎛ --- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝ ⎛ h exp ⎛ --- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝ (ξ + h) ∫ ξ (ξ + h ) ∫ ξ ⎞ ⎛ h h N̂ ( ξ' ) dξ'⎟ exp ⎛ --- D̂⎞ exp ⎛ --- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝2 ⎠ ⎠ ⎝ ⎞ ⎛ N̂ ( ξ' ) dξ'⎟ exp ( hD̂ ) exp ⎜ ⎠ ⎝ (ξ + h) ∫ ξ (ξ + h ) ∫ ξ ⎞ h N̂ ( ξ' ) dξ'⎟ exp ⎛ --- D̂⎞ U ( ξ, t ) = ⎝2 ⎠ ⎠ (13) ⎞ h N̂ ( ξ' ) dξ'⎟ exp ⎛ --- D̂⎞ U ( ξ, t ) ⎝2 ⎠ ⎠ 271 OPTICAL FIBER When the "Propagator Type" is set to "Runge-Kutta 4th order" (or "Runge-Kutta 2nd order") (RK4 or RK2), the exponent with the nonlinearity operator in Equation 8 is replaced by the direct integration of the following system of coupled ordinary differential equations: ⎛ ∂U -------⎞ = N̂U ⎝ ∂z ⎠ NL (14) by means of the standard RK4 (or RK2) routine (see example in [3]). The application of the dispersion operator is the same. Note: The Runge-Kutta (2nd or 4th order) implementations in the fiber component enable modeling the stimulated Raman scattering effect with the optical signal having an arbitrary polarization ("Model type" parameter set to "Vector"). However, due to the larger number of operations per step, they are executed slower and are not recommended otherwise (in "scalar" simulations or when the Raman effect is not included in a vector simulation) because the "Exponential" implementation of the nonlinearity provides faster execution. If the "Propagator type" is set to "Exponential" and "Calculation type" to "Iterative", Equation 11 is replaced by [2], [4]: ξ+h ∫ ξ N̂ ( ξ' ) dξ' ≈ h--- ( N ( ξ ) + N ( ξ + h ) ) 2 (15) N̂ ( ξ ) means N̂ ( E ( ξ ) ) . Since N̂ ( ξ + h ) is unknown at ξ + h ⁄ 2 , it is necessary to follow an iterative procedure that is initiated by replacing N̂ ( ξ + h ) by N̂ ( ξ ) (see [2], [4] for the details). Working with two iterations gives a reasonable The symbol combination between accuracy and speed, as recommended in [2]. 272 OPTICAL FIBER Figure 2 Evolution of E ( ξ, t = 0 ) 2 for N=3 soliton over 15 soliton periods with different calculation modes Note: In the three cases presented, NL ϕ max = 27.6mrad , constant step size. A comparison between the "Iterative" and "Noniterative" approaches is presented in Figure 2. Evolution of N=3 soliton over 15 soliton periods is presented. The "Step size" is kept "Constant" with the "Max. nonlinear phase shift" parameter is equal to 27.6. mrad. The noniterative approach is the fastest but not accurate enough at this step size. The development of spurious, numerical instability, which breaks the periodicity of the soliton evolution [2], is evident at the end of the run. For the same step size the iterative implementation of the split-step Fourier method suppresses the instability, thus improving the quality of the results, however this improvement is at the expense of increased computation time. h in the component is determined through the value of the parameter 2 = γmax ( E )h . In the case of the constant step size calculation, it is The step size NL ϕ max calculated once, using the input signal to obtain the maximum value of the intensity. In the case of variable step size calculation such an evaluation is performed at each step. 273 OPTICAL FIBER Figure 3 Variable step size, value of NL ϕ max is NL ϕ max = 50mrad In Figure 3, the calculation presented in Figure 2 is repeated using variable step size. This calculation takes longer in comparison to the "Noniterative" case presented in Figure 2, but less than in the case where two iterations are used. Depending on the behavior of the solution, variable step size calculation can take less time compared to the constant step size, although the fixed step size calculation performs a smaller number of operations per step (see Equation 13). In the presence of considerable attenuation, the importance of nonlinear effects decreases along the fiber length, which would permit the use of a larger step size. In this case, the use of variable step size will reduce the computation time. The variable step size calculation is more NL flexible, because different tasks can be handled keeping the value of ϕ max constant. For the case presented in Figure 3, this value is double the size of the one used in Figure 2, but the results are even better (refer to compare with Figure 2, "Noniterative"). The split-step scheme used in the model is locally second order accurate which 3 means that the local error is proportional to the h . However, the global error (after 3 2 N steps) is proportional to Nh = Lh [22]. Thus, increasing the fiber length might require decrease of the step size to maintain the same accuracy. The use of FFT implies periodic boundary conditions. In some cases a part of the pulse energy may spread eventually hitting the time window boundaries. When the energy reaches one of the edges of the time window it automatically reenters from the other edge perturbing the solution. This can be avoided using the absorbing type of boundary conditions. To achieve this at each step the optical field is multiplied in the time domain [10] by: Γ ( t ) = 1 – sech ( FilterSteepnes ( t – tedge ) ) , (16) where t edge indicates the nearest edge. The effect of periodic and absorbing boundary conditions is shown in Figure 4 where the results presented in Figure 3 from 274 OPTICAL FIBER "Birefringence and solitons" (propagation distance is equal to 1262.34km) are displayed. However here the time window is reduced to show the effect of the periodic boundary conditions. The oscillatory tail developed by the solution in the case when periodic boundary conditions are used is an unphysical effect, resulting from the interference of the radiation that has reentered the time window and the solution. In the case when absorbing boundary conditions are used the radiation that has separated from the solution is removed. The smaller the value of the filter steepness parameter the better the time window boundaries absorb (and do not reflect), however the larger part of the time window becomes absorbing (see Equation 16. Figure 4 Periodic (left plot) and absorbing with filter steepness 0.05 (right plot) boundary conditions 275 OPTICAL FIBER Vector approach When the polarization state of the incident light is not preserved during its propagation inside an optical fiber the scalar approach is no longer applicable and Equation 1 is replaced by [2], [6] - [10]: 2 3 ∂E ∂E iβ ∂ E β ∂ E 2 2 ---------X + β 1X ---------X + ------2- -----------X- – ----3- -----------X- = iγ ( 1 – ρ ) ⎛ E X + 2--- E Y ⎞ EX ⎝ ⎠ 2 3 ∂z ∂t 2 ∂t 6 ∂t 3 ∞ + iγρE X 2 ∫ h1111 ( s ) EX ( t – s ) ∞ 2 ds + ∫ h 1122 ( s ) E Y ( t – s ) ds 0 0 ∞ + iγρE Y ∫ h 1212 ( s )E X ( t – s )E Y∗ ( t – s )ds 0 2 (17) 3 ∂E ∂E iβ ∂ E β ∂ E 2 2 --------Y- + β 1X --------Y- + ------2- -----------Y- – ----3- -----------Y- = iγ ( 1 – ρ ) ⎛⎝ E Y + 2--- E X ⎞⎠ E Y ∂z ∂t 2 ∂t 2 6 ∂t 3 3 ∞ + iγρE Y ∫ h1111 ( s ) Eγ ( t – s ) 0 2 ∞ 2 ds + ∫ h 1122 ( s ) E X ( t – s ) ds 0 ∞ + iγρEX ∫ h 1212 ( s )Eγ t – s E∗ X ( t – s ) ds 0 Equation 17, h ijkl ( t ) contains the Raman response functions [6], [18]. Their Fourier transformations and Raman susceptibilities χ ijkl ( v ) , are shown in Figure 4.1. The convolution integrals in Equation 17 are evaluated in the frequency domain, by multiplying the spectra of the electric fields with the Raman susceptibilities and then performing the inverse FFT. 276 OPTICAL FIBER Figure 4.1 Raman susceptibilities for fused quartz [6, 18] The SRS effect is represented by "Intrapulse Raman scattering" (Equation 17) is replaced by [20]: 2 3 ∂E X ∂E iβ ∂ E β ∂ E --------- + β 1X ---------X + ------2- -----------X- – ----3- -----------X- = ∂z ∂t 2 ∂t 2 6 ∂t 3 iγ E X 2 2 2 1 +α ∂ EX ∂ EY 2 + ⎛ 2---( 1 – ρ ) + ρ --------------f⎞ E Y – ρτ R1 -------------- – ρτ R2 -------------- EX ⎝3 ⎠ 2 ∂t ∂t τ R1 – τ R2 ∂ ( E X E Y∗ ) – iγρ --------------------- ------------------------EY 2 ∂t (17a) 2 3 ∂E ∂E iβ ∂ E β ∂ E --------Y- + β 1Y --------Y- + ------2- -----------Y- – ----3- -----------Y- = ∂z ∂t 2 ∂t 2 6 ∂t 3 iγ E Y 2 2 2 2 1 +α ∂ EY ∂ EX + ⎛ 2---( 1 – ρ ) + σ --------------f⎞ E X – στ R1 -------------- – ρ τ R2 -------------- EY ⎝3 2 ⎠ ∂t ∂t τ R1 – τ R2 ∂ ( E Y E X∗ ) - ------------------------E X –iγρ --------------------2 ∂t Note: In the case of Equation 17 or Equation 17a, due to the orthogonal Raman gain terms (the last sections in Equation 17 or Equation 17a), the "Exponential" option for the "Propagator type" is not applicable. The component automatically selects "Runge Kutta 2nd order" when the model type is set to "Vector", and the Raman effect ("Intrapulse Raman scattering" or "Full Raman response" options 277 OPTICAL FIBER are selected. Due to the increased number of convolutions performed at each step the fiber component can be slow when solving Equation 17. In normalized units and when the SRS effect is neglected ( ρ reads as: 2 3 2 3 = 0 ) Equation 17 u – iD ∂-------u- + N ⎛ u 2 + 2--- v 2⎞ u = 0 i ⎛ ∂u ------ + δ ∂u ------⎞ + D 2 ∂-------3 1⎝ ⎝ ∂ξ ⎠ 2 3 ∂t 3 ⎠ ∂τ ∂τ (18) 2 2 ∂v- + δ ∂v i ⎛⎝ ---------⎞⎠ + D 2 ∂-------v- – iD 3 ∂-------v- + N 1 ⎛⎝ v + 2--- u ⎞⎠ v = 0 2 3 ∂ξ ∂t 3 ∂τ ∂τ The quantities β 1X and β 1Y are the inverse group velocities for the polarization components respectively. X and Y Figure 5 Optical fiber as a concatenation of trunks Note: The arrows represent the principal axes. The parameter δ is given byδ = ( β 1X – β 1Y )T 0 ⁄ ( 2 β 2 ), where β 1X – β 1Y is the value of the differential group delay parameter entered from the "PMD" tab, in the case where "Deterministic" mode is selected for the birefringence effect (see "Birefringence and solitons" from the Tutorials). The effects of four-wave mixing between the orthogonal polarization components are not taken into account due to their negligible contribution for typical values of the birefringence [9], [10]. The τ is introduced according to τ = ( t – β 1 z ) ⁄ T 0 where β 1 = ( β 1X + β 1Y ) ⁄ 2 . All the other parameters have the same meaning as in the normalized time scalar case. The "coarse-step method" [11] is used to simulate the PMD effects in the "Stochastic" mode. The fiber is represented by a concatenation of trunks and the propagation of light in each trunk is simulated by the split-step Fourier method described in the previous section. The lengths of the trunks are random numbers with a Gaussian 278 OPTICAL FIBER distribution [12]. The average and the dispersion of this distribution are the "Scattering section length" L scatt and "Scattering section dispersion" σ scatt parameters: i f ( L scatt ) i 2 ( L scatt – L scatt ) 1 - exp –-----------------------------------------= ----------------------2 2πσ scatt 2σ scatt (19) It is recommended [12] that the dispersion is 20% of the average value. The birefringence of each trunk is given by [11] (see the related PMD examples in the tutorials): DP d - ( Δβ ) = --------------------dω i L scatt (20) where D PMD is the PMD coefficient. The principal axes of the trunks are randomly oriented with respect to each other (see Figure 4). To simulate the random mode coupling at the end of each trunk the following transformation is applied [11], [13]: E X' E Y' In Equation 20, [ 0, 2π ] . = cos α sin α exp ( iϕ ) E X – sin α exp ( – i ϕ ) cosα EY (21) α and ϕ are random numbers uniformly distributed in the interval Wavelength dependent parameters The file that specifies the wavelength dependence of the parameters consists of two columns with the left column being the wavelength in nanometers and the right column containing the corresponding values of the parameters (see Table 1 ). The sampling interval is not necessarily be constant. The parameter values must be given in the units specified in the "Units" tab of the table. 279 OPTICAL FIBER Table 1 Wavelength dependence of the attenuation parameter λ [ nm ] α [ dB ⁄ km ] 1400 0.31405 1402.5 0.30246 1405 0.29276 1407.5 0.28457 1410 0.27757 1412.5 0.27153 The values of the parameters in Equation 1 and Equation 17 are evaluated at the reference wavelength. Note: The reference wavelength must be within the wavelength interval covered by the files for all the wavelength dependent parameters specified. The reference wavelength can be either user-specified or "automatic". In the last case the wavelength corresponding to the central frequency of the spectrum of the signal is assumed by the component to be the reference wavelength. Linear interpolation is used to calculate the values of the attenuation, effective area and n 2 parameters at this wavelength. For the dispersion parameters the following procedure is used. The wavelength dependence specified by the file is fitted internally using the five-term Sellmeier formula [14]. The higher-order dispersion parameters are then obtained by analytically differentiating this expression. If the option frequency domain parameter is unchecked, the file may give either the group delay β 1 ( λ ) or dispersion D ( λ ) (depending on the choice made in the "Dispersion file format" tab), and if the frequency domain parameters option is selected, either β 1 ( λ ) or β 2 ( λ ) can be supplied, again determined by the value of the "Dispersion file format" parameter. If the wavelength dependence of the group delay is given by the user, two successive differentiations are applied to its Sellmeier fit. Differentiating the analytical fit instead of using a direct numerical differentiation of the data provides the advantage of being able to produce reasonable results even in the case where the supplied data is noisy (see Appendix 1). Note: The accuracy of the Sellmeier fit depends on the type of the fiber. This is shown in Figure 6, where the results obtained for dispersion flattened and dispersion shifted fibers are shown. 280 OPTICAL FIBER Figure 6 Comparison between the original dispersion data and their fits for two fiber types Guidelines for using the component for WDM simulations Periodic boundary conditions are required for simulating the propagation of long bit sequences at different carrier wavelengths, which is the case when WDM systems are designed. To avoid the aliasing phenomena (see e.g. [3]), the sample rate is chosen to be at least three times bigger (Figure 7) than the bandwidth occupied by the simulated channels (see e.g. [15]). Figure 7 WDM channels and their four-wave mixing products Any frequency component outside the frequency range (Fc-SR/2, Fc+SR/2), where SR is the sample rate and Fc is the reference frequency is falsely translated (aliased) into that range by the very act of discrete sampling [3]. If the sample rate is bigger than the bandwidth occupied by the WDM channels (so it can accommodate all the channels) but less than three times that value in the presence of nonlinear effect the four-wave mixing products resulting from the nonlinear interaction between the channels (spurious waves [16]) will be aliased. In [16], to minimize the amount of 281 OPTICAL FIBER aliased power the requirement that the value of the power spectrum at the boundary of the available spectral range be -40 dB of its peak value is used. The longitudinal step size depends on the importance of the nonlinear effects for the particular simulation. If all the nonlinear effects are disabled step size equal to the fiber length will be used. The increase of the impact of nonlinearity will require decrease of the step size (decrease of the value of the max. nonlinear phase shift parameter) to maintain the same accuracy. Figure 8 Output spectra corresponding to NL NL ϕ max = 50mrad and ϕ max = 3mrad Note: The propagation distance is 100km. Input configuration is given in "Crossphase modulation" in the Tutorials. Values in the order of a few miliradians (one [15] and three [17])) are used with this parameter in a WDM system simulation. The effect of an improperly chosen step size is shown in Figure 8, where the output spectra corresponding to an interaction of two Gaussian pulses with carrier wavelengths one nm spaced are shown (see "Crossphase modulation" from the Tutorials). While the correct result that the four-wave mixing products (or spurious waves) should disappear when the pulses are no longer over-lapped (in the absence of any loss and gain [16]) is reached when the step-size is small enough, in the opposite case, the spurious frequencies present in the output spectra are still evident. The improperly chosen step size (too big) tends to exaggerate the four wave mixing products (see [22] and references therein). To increase the accuracy, you can switch from a "Noniterative" to an "Iterative" calculation type, keeping the step size the same (with the same step size, the "Iterative" implementation is more accurate, (see Figure 2), or alternatively, to keep working in the "Noniterative" mode and decrease the step size, or the value of the "Max. nonlinear phase shift" parameter. With respect to saving computational time, the latter strategy is better. It should be noted that computational time will not be saved by simultaneously increasing the number of iterations and the step size. 282 OPTICAL FIBER Appendix 1 Dispersion fitting according to the Sellmeier formula When the option "Dispersion from file” is selected, the dispersion data are internally fitted according to the five-term Sellmeier formula [14], namely: τ = c1λ where –4 + c2 λ –2 2 + c3 + c4 λ + c5 λ (1)A 4 τ is the group delay (per unit fiber length) or, respectively: dτ- = c 'λ –5 + c 'λ – 3 + c 'λ + c 'λ 3 D = ----1 2 4 5 dλ (2)A where D is the dispersion [ps/nm/km]. The user supplies data either for the dispersion or the group delay that are then fitted according to Equation 2A or Equation 1A, and the slope and/or dispersion are calculated by differentiating Equation 1A and Equation 2A analytically. The least-square fitting associated with Equation 2A amounts to minimizing: N Q = ∑ –5 –3 3 2 ( c 1λ i + c 2λ i + c 4λ i + c 5λ i – D i ) = min (3)A i=1 where N is the number of points. Using: ∂Q ------- = 0, i = 1…4 , ∂c i (4)A 283 OPTICAL FIBER the following linear system is obtained: – 10 –8 –4 –2 ∑ λi ∑ λ i ∑ λi ∑ λ i –8 –6 –2 ∑ λ i ∑ λ i ∑ λi N –4 –2 2 4 ∑ λi ∑ λi ∑ λi ∑ λi –2 4 6 ∑ λi N ∑ λi ∑ λi –5 C1 C2 C4 = C5 ∑ Diλ i –3 ∑ Diλ i ∑ Diλ i 3 ∑ Diλ i (5)A which is solved by LU-decomposition [3]. In the case when the user supplies a group delay data file, Equation 1A is used and Equation 5A transforms into Equation 6A. The fitting procedure is useful when/if noisy data is supplied by the user, as the following example shows. Figure 1A shows dispersion-versus-wavelength dependence of SMF-28 and the corresponding "exact" results for dispersion parameters are displayed below the graph. –8 –6 –4 –2 ∑ λ i ∑ λ i ∑ λi ∑ λ i –6 –4 –2 ∑ λ i ∑ λ i ∑ λi N –4 –2 2 ∑ λi ∑ λi N ∑ λi –2 2 4 ∑ λ i N ∑ λi ∑ λ i 2 4 6 N ∑ λ i ∑ λi ∑ λ i 284 N 2 λi ∑ 4 ∑ λi 6 ∑ λi 8 ∑ λi –4 C1 C2 C3 = C4 C5 ∑ τiλ i –2 ∑ τiλ i ∑ τi 2 ∑ τiλ i 4 ∑ τiλ i (6)A OPTICAL FIBER Figure 1A Lambda = 1550.75nm beta2=-2.08625e-026 s2/m beta3=1.27246e-040 s3/m D= 1.63411e-005 s/m2 S= 56.9931 s/m3 To assess the influence of noise on the results from the calculation some noise is added to the data presented in Figure 1A with the resulting graph presented in Figure 2A. Supplying the data from Figure 2A to the Nonlinear Dispersive Fiber Total Field component gives the results for the dispersion parameters presented under Figure 2A. 285 OPTICAL FIBER Figure 2A Lambda = 1550.75nm beta2=-2.10115e-026 s2/m beta3=1.32966e-040 s3/m D= 1.64578e-005 s/m2 S= 60.3521 s/m3 286 OPTICAL FIBER Appendix 2 Optical fiber data SMF-28 The SMF-28 model used in OptiSystem has the following characteristics: Figure 1 Attenuation Figure 2 Group Velocity Dispersion 287 OPTICAL FIBER Figure 3 Effective Area Figure 4 Group Delay Attenuation curve shows a minimum of GVD curve reveals a dispersion of 2 slope of 0.05 ps/nm ⁄ km . Effective area at Group delay is 0.185 dBm for a wavelength of 1550 nm . 16.5 ps/nm/km at 1550 nm with a dispersion 2 1550 nm is 76.5 μm . 4897650 ps/km . This model can be varied in any way because you have the ability to change any particular parameter. Create a new file and then load it into the appropriate section, or just set the parameter to 'Constant' and enter a value. The Nonlinear Fiber model is very flexible, because it has the ability to model practically every manufactured fiber that exists on the market today. 288 OPTICAL FIBER +D NZDSF model The +D NZDSF model used in OptiSystem has the following characteristics: Figure 5 Attenuation Figure 6 Group Velocity Dispersion 289 OPTICAL FIBER Figure 7 Effective Area Figure 8 Group Delay Attenuation curve shows a minimum of GVD curve reveals a dispersion of 2 slope of 0.01 ps/nm ⁄ km . The effective area at Group delay is 290 0.185 dBm for a wavelength of 1550 nm . 4.5 ps/nm/km at 1550 nm with a dispersion 2 1550 nm is 71.5 μm . 4895870 ps/km . OPTICAL FIBER -D NZDSF model The -D NZDSF model used in OptiSystem has the following characteristics: Figure 9 Figure 10 Attentuation Group Velocity Dispersion 291 OPTICAL FIBER Figure 11 Effective Area Figure 12 Group Delay Attenuation curve shows a minimum of GVD curve reveals a dispersion of 2 slope of 0.18 ps/nm ⁄ km . Effective area at Group delay is 292 0.185 dBm for a wavelength of 1550 nm . – 7.5 ps/nm/km at 1550 nm with a dispersion 2 1550 nm is 92 μm . 4890750 ps/km . OPTICAL FIBER CDF (Standard) The DCF model used in OptiSystem has the following characteristics: Figure 13 Figure 14 Attenuation Group Velocity Dispersion 293 OPTICAL FIBER Figure 15 Effective Area Figure 16 Group Delay 0.3 dBm for a wavelength of 1600 nm . Attenuation curve shows a minimum of GVD curve reveals a dispersion of 2 slope of 4.5 ps/nm ⁄ km . Effective area at Group delay is 294 – 82 ps/nm/km at 1550 nm with a dispersion 2 1550 nm is 32 μm . 4914000 ps/km . OPTICAL FIBER References: [1] G. P. Agrawal, "Applications of nonlinear fiber optics", Academic press, 3rd edition, 2001. [2] G. P. Agrawal, "Nonlinear fiber optics", Academic press, 3rd edition, 2001. [3] W. H. Press, et al., "Numerical Recipes: The Art of Scientific Computing", 2nd Edition, Cambridge University Press, 1992. [4] M. Lax, J. H. Batteh and G. P. Agrawal, Journ. Appl. Phys. 52 , 109, (1981). [5] F. Matera and M. Settembre, Journ. Lightwave Technol. 14, 1 (1996). [6] R. W. Hellwarth, Prog. Quant. Electr. 5, 1 (1977). [7] E. A. Golovchenko and A. N. Pilipetskii, JOSA B, 11, 92 (1994). [8] P. T. Dinda, G. Millot, and S. Wabnitz JOSA B, 15, 1433 (1998). [9] C. R. Menyuk, Opt. Lett., 12, p. 614 (1987). [10] C. R. Menyuk, JOSA B, 5, p. 392(1988). [11] D. Marcuse, C. R. Menyuk and P. K. A. Wai JLT, vol. 15, No. 9, pp. 1735 (1997). [12] C. H. Prola Jr., J. A. Pereira da Silva, A. O. Dal Forno, R. Passy, J. P. Von der Weid, and N. Gisin IEEE Phot. Technol. Letters, 9, No. 6, 842 (1997). [13] P. K. A. Wai, C. R. Menyuk, and H. H. Chen , Opt. Lett. 16 1231 (1991). [14] L. G. Cohen, Journ. Lightwave Technol. 3, 958, (1985). [15] M. I. Hayee and A. E. Willner, IEEE Phot. Technol. Lett. 11, No. 8, (1999). [16] D. Marcuse, A. R. Chraplyvy, and R. W. Tkach, Journ. Lightwave Technol, 9, 121 (1991). [17] R. W. Tkach, A. R. Chraplyvy, F. Forghieri, A. H. Gnauck, and R. M. Derosier, Journ. Lightwave Technol, 13, 841 (1995). [18] P. Tchofo Dinda, G. Millot, and S. Wabnitz, JOSA B, 15, 1433, (1998). [19] R.H.Stolen, J.P.Gordon, W.J. Tomlinson and H.A. Haus, JOSA B, 6, 1159 (1989). [20] C.R.Menyuk, M.N.Islam and J.P.Gordon, Optics Letters, 16 566, (1991). [21] K.J. Blow and D. Wood, IEEE J. Quant. Electr., 25, 2665, (1989). [22] O. Sinkin, R. Holzlohner, J. Zweck and C. R. Menyuk, Journ Lightwave Technol. 21, 61 (2003). 295 OPTICAL FIBER Notes: 296 OPTICAL FIBER CWDM Optical fiber CWDM The component simulates the propagation of arbitrary configuration of optical signals in a single-mode fiber. Dispersive - first and second order group velocity dispersion (GVD) effects - and non- self-phase modulation (SPM), cross-phase modulation (XPM) and stimulated Raman scattering (SRS) effects - are taken into account. The evolution of each sampled signal is governed by a modified nonlinear Schrödinger (NLS) equation (when the signal is assumed to maintain its state of polarizing) or a system of two, coupled NLS equations (arbitrary polarization state of the signal). Raman interaction for an arbitrary configuration of sampled and parameterized signals is also considered. Noise bins also participate in the SRS effects, however their power is assumed much smaller than that of the parameterized and sampled signals, which means that the SRS interaction between noise bins and parameterized/sampled signals is considered as a pump-probe interaction. The component provides most of the functionality of the total field approach fiber model (excepting the simulation of the Raman effect in birefringent fibers) while at the same time, it can handle different signal representation to give more flexibility and speed up the calculations. Ports Name and description Port type Signal type Input Input Optical Output Output Optical 297 OPTICAL FIBER CWDM Parameters Main Name and description Symbol Default value Units Value range Merge sample bands — False — False, True — True — True, False λ0 1550 nm [100, 2000] L 50 km [0, 100 000] — True — True, False — Constant — Constant, From File If TRUE all the sampled signals will be re-sampled and a single frequency band confining all the sampled signals will be formed. As a result the "Total field approach" (see the technical description of the total field fiber model for the details) will be implemented in the simulation. This will include the effects of four-wave mixing in the simulation and, besides the SRS effect will be represented through the convolution integral of the Raman response function and the field intensity. If FALSE all the channels will be treated separately - FWM effects will be disabled and SRS effects will be approximated through inter band Raman scattering [1, 2]. User defined reference wavelength If TRUE the frequency corresponding to the value entered under "Reference wavelength" is used internally as reference frequency.. The system of modified NLS equations governing the evolution of the signals is solved in a frame moving with the group velocity corresponding to that frequency. If FALSE the value of the reference frequency is calculated as the averaged of the central frequencies of all the sampled and parameterized signals. Reference wavelength The value of the user specified reference wavelength. Length Fiber length Attenuation effect If TRUE the attenuation effect is enabled, and vice versa. Attenuation data type Defines if the attenuation value will be read from the "Attenuation" tab or from a file. If "Constant" the value specified in the "attenuation" tab will be used for all sampled, parameterized signals and noise bins. If "From file" a separate value will be calculated for each noise bin, parameterized or sampled signal by interpolating the data file. 298 OPTICAL FIBER CWDM Name and description Symbol Default value Units Value range Attenuation α 0.2 dB/km [0, 1010] — — — — Name and description Symbol Default value Units Value range Group velocity dispersion — True — True, False — True — True, False — False — True, False — Constant — Constant / FromFile The specified value will be used for all signals if "Attenuation data type" is set to "Constant". If "Attenuation data type" is set to "From file" the value will be ignored. Attenuation vs wavelength If "Attenuation data type" is set to "From file" this field specifies the file containing the attenuation data. In this case the attenuation effect is wavelength dependent for all types of signals values corresponding to the central frequency of each signal will be calculated by linear interpolation and used internally. Dispersion If TRUE the GVD effect is enabled. Third order dispersion If TRUE the TOD effect is enabled. Dispersion data type Defines if the dispersion parameter values will be read from the tabs or from a file. If "Constant" the values from the tabs will be used to calculate the relative group delay, and first order GVD for each sampled signal by Taylor expansion around the reference wavelength. Otherwise (parameter set to "From file") group delay, first- and second order GVD parameters corresponding to each sampled signal will be calculated from the user-specified file by Sellmeier fitting. While "Frequency domain parameters" is TRUE, "Dispersion data type" will remain "Constant" and cannot be changed. This is done since the only acceptable format for the file specifying the dispersion is group delay vs. wavelength. Frequency domain parameters Defines the domain in which the dispersion parameters are specified. If TRUE frequency domain is used and the dispersion effect is specified in terms of and . Otherwise the wavelength domain is used (D and S). This parameter is meaningful (and, hence, enabled) only if "Dispersion data type" is set to "Constant". 299 OPTICAL FIBER CWDM Name and description Symbol Default value Dispersion β2 -20 β3 0 D 16.75 Units Dispersion slope — [-10100, 10100] ps -----------------------( nm ) ( km ) 0.075 ps --------------------------2 ( nm ) ( km ) [-10100, 10100] — — — The value of the TOD parameter in the frequency domain. Dispersion file name 3 [-10100, 10100] The value of the GVD parameter in the frequency domain. Beta 3 [-10100, 10100] ps -------km The value of the dispersion slope parameter in the wavelength. Beta 2 2 ps -------km The value of the GVD parameter in the wavelength domain. Value range Specifies the file with the dispersion data. PMD The notation "Frequency domain parameters" refers to the alternative definitions ∂β D = --------1-, S = ∂D ------- (wavelength domain definition) and ∂λ ∂λ ∂β ∂β β 2 = --------1-, β 3 = --------2- (frequency domain definition). ∂ω ∂ω However, the format of the file specifying the wavelength dependence of the dispersion is the following: the first column of the file contains wavelength values and the second column, the corresponding values of (λ) , β 1 ( λ ) . Consequently, "Frequency domain parameters" is meaningless when the dispersion is specified from a file. Name and description Symbol Default value Units Value range Birefringence type — Deterministic — Deterministic /Stochastic Determines the type of birefringence. If "Deterministic" is selected both the strength of birefringence and principal axes are assumed constant, hence random mode coupling is disabled. If "Stochastic" is selected the random mode coupling is enabled. 300 OPTICAL FIBER CWDM Name and description Differential group delay If "Birefringence type" is set to "Deterministic" this is the value of the differential group delay. If "Birefringence type" is set to "Stochastic" the parameter is disabled. Symbol Default value d - ( Δβ ) -----dω ps-----km Dp 0.5 Mean scattering section length L scatt 500 σ scatt 100 Scattering section dispersion The dispersion of the scattering section length. Value range [-10100, 10100] 0.2 PMD Coefficient The averaged value of the fiber length at which the polarization state of the signal is randomized by applying the scattering matrix. Units [0, 10100] ps ---------km [0, 10100] m [0, 10100] m In the case when more than one sampled signal (separated channels) is propagating in the fiber, the PMD-induced penalties will be the same for all channels. Different penalties (and Q-factors) will be obtained if all the channels are merged (total field approach). Birefringence and random mode coupling does not affect parameterized signals and noise bins. Nonlinearities Name and description Symbol Default value Units Value range Self-phase modulation — True — True, False — True — True, False Determines if the self-phase modulation (SPM) effect will be taken into account. If FALSE, all the nonlinear effects - XPM, SRS - will be disabled. Cross-phase modulation Determines if the XPM effects are taken into account. The parameter is active provided that the SPM effects are enabled. In the scalar case XPM includes the interactions among all parameterized and sampled signals. In the vector case only interactions between sampled signals are considered and the XPM between orthogonal polarization components is also included. 301 OPTICAL FIBER CWDM Name and description Symbol Default value Units Value range Effective area data type — Constant — Constant/ FromFile A eff 80 — — — — — — — Constant/ FromFile n2 2.6x10-20 — — — — — False — True/False Defines if the effective area parameter value will be read from the tab or from a file. If "Constant" the value from the tab will be used. Otherwise the parameter is treated as wavelength dependent and a separate value corresponding to the center frequency of each sampled signal, parameterized signal and noise bin is calculated and used. Effective area The value of the effective area parameter. This value will be used if "Effective area data type" is set to "Constant". Otherwise the value will be ignored. Effective area vs wavelength μm 2 [0, 1010] If the "Effective area data type" is set to "From file" then this tab specifies the file containing the effective area data. n2 data type Defines if the n2 parameter (nonlinear index of refraction) value will be read from the tab or from a file. If "Constant" the value from the tab will be used. n2 The value of the n2 parameter. If "n2 data type" is set to "Constant" this value will be used. Otherwise it will be ignored. n2 vs wavelength 2 m -----W [0, 10100] If the "n2 data type" is set to "From file" then this tab specifies the file containing the nonlinear index of refraction wavelength data. Inter-band Raman scattering One of the two possible alternative representations of the SRS effect in the model that leads to energy exchange between different frequency bands. Interactions among all sampled signals, parameterized signals and noise bins are considered. Noise bins are treated as a weak probe with respect to the sampled signals and parameterized signals the latter are treated as pumps. Inter-band Raman scattering [1-7] is an approximation to the full expression of the Raman polarization valid provided that the frequency separation of the interacting signals is much larger than their individual spectral bandwidths. SRS effect can be enabled only in the scalar case (fixed polarization state, "Model type" from the numerical tab should be set to "Scalar" to enable SRS). If this representation for the SRS effect is used the model runs faster. 302 OPTICAL FIBER CWDM Name and description Symbol Default value Units Value range Complete Raman response — False — True/False — False The other alternative representations for the SRS effect, leading to coupling of signals occupying different frequency bands. In this case no assumption about the ratio between the bandwidth of the sampled signals and their frequency separation is made. Convolution integrals are calculated to represent the interaction of sampled signals with sampled signals, with noise bins and parameterized signals and vice versa. This is a more accurate description however the speed of the calculations in this case is lower. The interaction of noise bins with parameterized signals is always represented through inter-band Raman scattering i.e. the individual bandwidth of noise bins and parameterized signals is always considered zero. The parameter "Complete Raman response" is responsible only for this part of the Raman polarization that leads to energy exchange between different frequency bands. It does not include the Raman contribution to XPM and SPM. In case only one sampled signal and zero noise bins and parameterized signals propagate in the fiber, the two alternative descriptions of the SRS effect become completely equivalent. This is the case when the model works in the "Total filed approach" mode. However if "Complete Raman response" is selected, the "Molecular SPM and XPM" should be set to TRUE to achieve this equivalence while this is done automatically if "Inter-band Raman scattering" is selected to represent the SRS effect and only one sampled signal propagates in the fiber. Both parameters "Molecular XPM and SPM" and "Complete Raman response" are enabled if "Model type" is set to Scalar. Molecular XPM and SPM True/False The contribution to SPM and XPM stemming from the delayed (Raman) nonlinear response. This effect is meaningful for sampled signals only, since no phase is considered for Noise bins and Parameterized signals. In the presence of one sampled signal only molecular XPM is zero and the effect is reduced to molecular SPM. Molecular SPM might me important (and should not be neglected) despite that the energy transfer between different frequency components of the only sampled band present due to SRS is negligible. The parameter "Molecular XPM and SPM" is disabled if "Inter-band Raman scattering" is selected to represent the SRS, since the delayed part of the SPM and XPM is automatically included in this case. Both parameters "Molecular XPM and SPM" and "Complete Raman response" are enabled if "Model type" is set to Scalar. 303 OPTICAL FIBER CWDM Name and description Symbol Fractional Raman contribution ρ The fraction of the nonlinear polarization, related to the stimulated Raman scattering effect [1]. Default value Units Value range 0.18 — [0,1] Numerical Name and description Symbol Default value Units Value range Model type — Scalar — Scalar/Vector — Variable — Variable/ Constant Defines the model type used for the simulation depending on the polarization state of the signal. If "Vector" is selected the signal can have arbitrary polarization state and a system of two coupled equations, corresponding to each polarization component (x or y) of every sampled signal is solved. If "Scalar" is selected it means that all the signals preserve their polarization state and a single equation (1) is solved for each sampled band. Vector simulation will be performed, regardless of the value of the model type parameter, in the following two cases1)Two polarization components are detected at the fiber input. This will work for sampled noise, since the noise is unpolarized and x- and y-polarization components are stored independently in the memory. Sampled signals with well defined polarization state however might use a different method of storage in the memory and, consequently, this parameter should be set to "Vector" manually if the polarization evolution is to be considered. 2)The PMD effect is set to stochastic.Turning the "vector" on will disable SRS. Step size Specifies whether variable or fixed step-size simulation will be used. If "Variable" is selected the step size is adaptively changed depending on the value of the "Max. nonlinear phase shift" parameter and the behavior of solutions itself. Otherwise the step size is evaluated only once, at the beginning of the simulation. In some cases the fixed step size calculation executes faster, due to the smaller number of calculations per step, but the variable step size calculation is more flexible and can be faster in the presence of strong attenuation. 304 OPTICAL FIBER CWDM Name and description Max. nonlinear phase shift Maximum (over the time window) phase shift induced by the self-phase modulation effect per step is calculated for each sampled signal. SPM induced phase shifts are then calculated for each parameterized signal. Then the step size is calculated in such a way that the maximum (over the entire set of signals) SPM-induced phase shift is equal to the specified value. Boundary conditions Symbol NL ϕ max Default value Units [0,10100] 3 mrad — Periodic — Periodic/ Absorbing — 0.5 — [0,10100] Specifies the type of boundary conditions used for the simulation. Filter steepness Value range In case "Boundary conditions" option is set to "Absorbing" the "Filter steepness" parameter determines the absorption/reflection properties of the time window boundaries. The same absorbing boundary conditions are used for all sampled signals. Graphs. Name and description Symbol Default value Units Value range Calculate graphs — False — True/False — 200 — [1, 100000000] — 200 — [1, 100000000] — False — True/False Enable / disable the 3D graphs. If disabled, no graphs will be plotted and no data is stored. Graphs are plotted for sampled signals only. Number of distance steps The number of longitudinal (or in z) snapshots (slices) that will be used to construct a 3D plot. Increasing this value will make the 3D graph to look better. The number of snapshots that are stored cannot be bigger than the number of steps in z taken by the simulation to obtain the solution. The latter is determined by the maximum nonlinear phase-shift parameter (numerical tab). Number of wavelength/time steps The number of stored points (in t) per snapshot. Increasing this value will make the 3D graph to look better. Linear scale Determines the axis-type (linear or logarithmic) for the dependent variable. If TRUE the axis type is linear. 305 OPTICAL FIBER CWDM Name and description Symbol Default value Units Value range — Wavelength range — Wavelength range/One sampled signal The next six parameters in this tab determine which graphs will be plotted after the simulation is finished. Plot type Determines the type of the plot that will be created in either frequency or time domain. If the parameter is set to "Wavelength range" than a copy of each sampled signal residing in the specified wavelength range will be created, this copies will be up-sampled and merged in a single frequency band. This single frequency band, containing all the signals will be plotted in either frequency or time domain. The merging does not affect the signals but their copies only, so multiple sampled signals will be involved in the simulation. If the parameter is set to "Plot one sampled signal" a 3D graph presenting the sampled signal with central frequency given by "Signal center frequency" will be created. Simulation Name and description Symbol Default value Units Value range Enabled — True — True/False Determines whether the component is enabled. If FALSE, all the input signals reach the output port of the component without any change. Noise Name and description Symbol Default value Units Value range Convert noise bins — False — True/False If TRUE each noise bin within the bandwidth of the signal will be converted to a Gaussian white noise, with the correct power spectral density, and this noise will be added to the signal. 306 OPTICAL FIBER CWDM Random numbers Name and description Symbol Default value Units Value range Generate random seed — False — True/False — 0 — [0, 4999] Determines how the random number generator is initialized (seeded). If TRUE the seed index used for this initialization is a random number itself. Otherwise user specified number is used for this purpose. Random seed index If "Generate random seed" is set to TRUE this value specifies the seed index. The generated pseudorandom sequence is one and same provided the seed index is not changed. The value of "Random seed index" will be ignored if "Generate random seed" is set to TRUE. Technical Background Scalar approach Signal propagation equations with Inter-band Raman scattering When the optical field is assumed to maintain its polarization along the fiber length (so called scalar approach, Model type parameter from the "Numerical" tab is set to "Scalar") the evolution of the slowly varying electric field envelopes sampled signals (SS), powers powers { E i } of a set of { P l } of another set of parameterized signals (PS) and { N m } of a third set of noise bins (NB) is governed by the set (1) of equations. The subsystem (1a) consists of Number of SS (the total count of sampled signals) coupled nonlinear Schrödinger (NLS) [1], [2], (1b) contains Number of PS equations (the total count of PS) and (1c) - Number of NB (the total count of NB) equations. 307 OPTICAL FIBER CWDM 2 3 ∂E i iβ 2 ( ω i ) ∂ E i β 3 ( ω i ) ∂ E i ∂E -------- + ( β l ( ω i ) – β l ( ω 0 ) ) --------i + α ( ω i )E i + ----------------- ---------- – ---------------- ---------- = 2 ∂z ∂T 2 6 ∂T 3 ∂T Number of SS ∑ (2 – ρ) iγ i ∑ Number of PS 2 E k – ( 1 – ρ ) Ei + ( 2 – ρ ) k=1 Number of SS ρ 2 ∑ Ei l=1 ( SS ) R ik 2 Number of PS Ek + ρ k=1 ∑ ( PS ) R il (1a) + Pl l=1 Number of PS ( PP ) ⎛ ⎞ ⎜ ⎟ ∑ Rlh Ph + ⎜ ⎟ dP l h=1 -------- = – 2α l P l + 2ργl P l Im ⎜ ⎟ Time window Number of SS dz ⎜ ⎟ ( SP ) 2 1 ⎜ -------------------------------⎟ R E t d t li i ∑ ∫ ⎝ Time window ⎠ i=l Number of PS ( PP ) ⎛ ⎜ ∑ Rmh Ph + ⎜ dN m h=1 --------- = – 2αm N m + 2ργ m N m Im ⎜ Number of SS dz ⎜ ( SN ) 1 ⎜ -------------------------------R mi ∑ ⎝ Time window i=l 308 (1b) 0 ⎞ ⎟ ⎟ ⎟ Time window ⎟ 2 ⎟ E t d t i ∫ ⎠ 0 (1c) OPTICAL FIBER CWDM The Raman matrices are defined according to: ( SS ) R ik ⎧ ⎪ R = ⎨ χ 1111 ( f i – f k ), i ≠ k 1 ≤ i ≤ Number of SS, 1 ≤ k ≤ Number of SS ⎪ 0, i=k ⎩ ( PS ) R il ⎧ ⎪ R = ⎨ χ 1111 ( f i – f l ), f i ≠ f l 1 ≤ i ≤ Number of SS, 1 ≤ l ≤ Number of PS ⎪ 0, fi = fl ⎩ ( PP ) R lh ⎧ ⎪ R = ⎨ χ 1111 ( f l – f h ), l ≠ h 1 ≤ l ≤ Number of PS, 1 ≤ h ≤ Number of PS ⎪ 0, l=h ⎩ ( SP ) R li ⎧ ⎪ R = ⎨ χ 1111 ( f l – f i ), f l ≠ f i 1 ≤ l ≤ Number of PS, 1 ≤ i ≤ Number of SS ⎪ 0, f l = fi ⎩ ( PN ) R mh ⎧ ⎪ R = ⎨ χ 1111 ( f m – f h ), f m ≠ f h 1 ≤ m ≤ Number of NB, 1 ≤ h ≤ Number of PS ⎪ 0, f m = fh ⎩ 309 (2a) (2b) (2c) (2d) (2e) OPTICAL FIBER CWDM ( SN ) R mi ⎧ ⎪ R = ⎨ χ 1111 ( f m – f i ), f m ≠ f i 1 ≤ m ≤ Number of NB, 1 ≤ h ≤ Number of SS ⎪ 0, fm = f i ⎩ (2f) Raman susceptibility for fused quartz is shown in Figure 1. It should be noted that R R ∗ χ 1111 ( – ω ) = ( χ 1111 ( ω ) ) , where "*" means complex conjugation. Figure 1 Raman susceptibilities for fused silica [3, 4] E i = E i ( z, T ) is the electric field envelope of the i -th sampled signal. A frame moving at the group velocity ( T = t – z ⁄ v g ≡ t – β 1 ( ω 0 )z ) corresponding to the reference frequency ω 0 is assumed. In Equation (1a), The reference frequency is related to the parameter "Reference wavelength" ("Main" category of the component tool-box) through ω 0 = 2πc --------- with c being the light speed in vacuum. λ0 The derivatives of the propagation constant of the fiber mode β ( ω ) ( ( β ( ω )c ) ⁄ ω is the mode effective index). n β ( ω -) n = 1, 2 β n = ∂----------------n ∂ω are the first ( β 2 ) and second order ( β 3 ) group velocity dispersion (GVD) parameters and are evaluated at the center frequencies { ω i } of the sampled signals. With respect to frequency, 310 OPTICAL FIBER CWDM The nonlinear coefficients for every SS, NB, or PS in (1) are defined according to: ωj n2 ( ωj ) γ j = --------------------cA eff ( ω j ) (3) The meaning of the terms on the left-hand side of the subsystem (1a) is the same as in the total field approach fiber model (see the technical description of this component). The first two terms in the right hand side of (1a) give the SPM and XPM contributions of the remaining sampled signals. The third term is the XPM contribution of the PS. The fourth and the fifth term describe the SRS induced interactions between the i -th sampled signal and rest of the sampled signals and with the parameterized signals, respectively. Subsystems (1b) and (1c) describe the power balance of the set of PS and NB respectively. These are obtained by replacing the NLS equations for NB and PS with the time-averaged versions of their power conservation laws. In the absence of attenuation the total number of photons is conserved as (1) shows. The first terms in the right-hand sides of (1b) and (1c) take into account the attenuation effects. The second and the third terms in the right-hand side of (1b) describe the SRS induced power transfer between the l -th PS and the rest of the PS and between the l -th PS and the SS respectively. The second and the third terms in the right-hand side of (1c) are responsible for the SRS-induced interactions between noise bins and PS and noise bins and SS. Note that in describing the interactions through SRS between NB and SS and NB and PS the power of the noise bins is neglected with respect to that of PS and SS - i.e. all the NB are treated as a weak "probe". They change their power due to the interactions with SS and PS, however the amount of power transferred from SS and PS to NB is neglected with respect to the power of SS and NB. This approximation is valid, provided the power of NB remains much smaller compared to that of SS and NB. With multiple SS present in the fiber the SRS effect is represented through inter-band Raman scattering. This is an approximation to the full expression for the Raman polarization [1],[2] that is valid provided that the frequency separation between the interacting signals is large enough compared to their individual bandwidths. In the opposite case (frequency separation between the signals comparable with their individual spectral bandwidth) total field approach can be implemented by turning on the option "Merge sampled bands". In this case the system (1a) is replaced by the following single NLS Equation 4 and (1b) and (1c) remain unchanged. In Equation 4, the Raman response function h 1111 ( t ) is the Fourier transform of the Raman susceptibilities shown in Figure 1. Total field approach however should be used with some care. At first, in this case, (single sampled band) XPM and four wave mixing 311 OPTICAL FIBER CWDM effects are included automatically in the simulation and turning on or off the "XPM" parameter in the "Nonlinearities" tab will have no effect on the results. 2 iβ 2 ( ω 0 ) ∂ E i β 3 ( ω 0 ) ∂ 3 E ∂E ------ + αE + ------------------ ---------- – ----------------- --------- = 2 ∂z 2 6 ∂T 3 ∂T ∞ ⎛ 2 2 ⎜ ( 1 – ρ ) E + ρ ∫ h 1111 ( s ) E ( T – τ ) ds ⎜ 0 iγ ⎜ Number of PS ⎜ ( PS ) ⎜ +ρ R 1l P l ∑ ⎝ l=1 Figure 2 312 ⎞ +⎟ ⎟ ⎟E ⎟ ⎟ ⎠ (4) OPTICAL FIBER CWDM Figure 3 Total field approach implemented with improper choice of sample rate. The output probe power is 0.931 mW. Figure 4 The correct result is obtained when the bandwidth is high enough. Output probe power is 1.377mW. The slight difference in the output probe power could be attributed to FWM. The following example shows the importance of the proper choice of numerical parameters. Figure 2 shows the layout. The input consists of a strong (1 W power) pump wave at 193 THz and a weak (1 mW) probe wave at 192.5 THz. "Merge sampled bands" parameter of the optical fiber component is enabled, which means that total field approach will be used. Attenuation effect is disabled and we use "Constant" step size with the "Maximum nonlinear phase shift" parameter equal to 5 mrad. Raman effect is enabled The rest of the set-up of the optical fiber component is the default one. Since total field approach will be used enabling or disabling the "XPM" parameter will have no effect on the results. Figure 3 and Figure 4 show the obtained results together with the global parameters of the layout in each case. Figure 5 gives the result treating the two waves as separated channels - "Merge sampled bands" parameter is set to FALSE in the optical fiber component. In the case presented in Figure 3 the simulated bandwidth is too 313 OPTICAL FIBER CWDM small to accommodate the FWM mixing products of both waves and hence they are aliased (see e.g. [8]). This false translation of the frequency of the wave (known as aliasing) can put the a weak FWM product in the closed spectral vicinity of the pump which will trigger a strong FWM (or modulation instability since the signal wavelengths are in the anomalous GVD regime, which is also a kind of FWM) if the frequency separation is small, and consequently, the coherence length is large. The result is an entirely unphysical generation of new frequency components. Note that probe attenuation is obtained instead of probe amplification. Figure 4 gives the correct result since no aliasing occurs. This is achieved by having the simulated bandwidth (or equivalently the sample rate) high enough to accommodate the three times the input signal bandwidth. Figure 5 Simulation in which both signals are treated as separated channels. Output probe power is 1.371 mW. A comparison with Figure 5 (obtained treating the pump and the probe wave as two separate sampled bands) which gives the same output power for the probe wave as the total field approach with the sample rate correctly chosen shows that in this case FWM effects are quite small. Besides, treating the signals as separate frequency bands leads a significant reduction of the simulation time. It should be kept in mind however that while in the case of total field approach, all the parameters (dispersion, attenuation, etc.) are evaluated just once - at the reference frequency, here (when multiple SS are considered) a set of parameters is evaluated for each sampled signal - at the center frequency of the corresponding signal. The meaning of the reference frequency (and reference wavelength) is the following: The subsystem (1a) is written in a frame moving with group velocity corresponding to the reference wavelength - no other signal parameters are evaluated at this frequency. The reference wavelength can be either user-specified or "automatic", which corresponds to the averaged frequency of the center frequencies of all SS and PS. 314 OPTICAL FIBER CWDM If "Dispersion data type" is set to "Constant" the dispersion parameters specified in the tabs (D and S) or, respectively, β 2 and β 3 , are assumed to correspond to the reference wavelength. Hence, Taylor expansion is used in this case: 2 β 1 ( ω ) – β 1 ( ω 0 ) = β 2 ( ω 0 ) ( ω – ω 0 ) + 1--- β 3 ( ω 0 ) ( ω – ω 0 ) 2 Evaluating Equation 5 and its first and second derivatives with respect to (5) ω at the { ω 1 } gives the sets of parameters: { β 2 ( ω 1 ) – β 1 ( ω 0 ) }, { β 2 ( ω i ) } and { β 3 ( ω i ) } . signal frequencies It should be kept in mind however that with multiple sampled signals present, specifying nonzero β 2 and β 3 (or D and S) and disabling in the same time the "Group velocity dispersion" and "Third order dispersion" will result in { β 2 ( ω i ) = 0, ∀i }, { β 3 ( ω i ) = 0, ∀i } , but { β 1 ( ω i ) ≠ β 1 ( ω j ), if i ≠ j } , which means that no GVD induced pulse broadening will be observed but pulses with different center frequencies will propagate with different group velocities. In contrary, if all the sampled signals are merged to form a single frequency band disabling the GVD effects will not only disable pulse broadening, but also will set the group velocity constant for the entire sampled band considered. If "Dispersion data type" is set to "From file" the data set specified by the file is Sellmeier fitted than dispersion parameters are calculated by analytically differentiating the fit. The file specifying the dispersion data must provide the dependence of group delay [ps/km] on the wavelength [nm]. For this reason "Frequency domain parameters" is disabled when "Dispersion data type" is set to "From file". 315 OPTICAL FIBER CWDM Signal propagation equations with "Complete Raman response" When the SRS effect is represented through "Complete Raman response" the system (1) is replaced by: 2 3 ∂E ∂E i iβ 2 ( ω i ) ∂ E i β 3 ( ω i ) ∂ E i -------- + ( β l ( ω i ) – β l ( ω 0 ) ) --------i + α ( ω i )E i + ----------------- ---------- – ---------------- ---------- = 2 ∂z ∂T 2 6 ∂T 3 ∂T Number of SS i 2 ∑ (2 – ρ) Number of PS 2 ∑ Ek – ( 1 – ρ ) E i + ( 2 – ρ ) l=1 k=1 Number of SS + iγ i ρ ∑ k = 1, k ≠ i ∞ E k ( T ) ∫ h 1111 ( τ )E i ( T – τ )E k∗ ( T – τ )e – i ( ω i – ω k )τ dτ (6a) 0 Number of PS ∞ + iγ i ρ Pl Ei ∑ l=1 ∫ h1111 ( τ )Ei ( T – τ )e – i ( ω i – ω l )τ dτ 0 ∞ Number of SS + iγ i ρE i ( T ) ∫ h 1111 ( τ ) 0 ∑ 2 E k ( T – τ ) dτ k=1 ⎛ Number of PS ( PP ) ⎞ dP l -------- = – 2α l P l + 2ργ l P l Im ⎜ ∑ Rlh Ph⎟⎠ + dz ⎝ h=1 2ργ l Pl ---------------T.W. 316 Number of SS T.W. ∑ i=1 ∫ 0 ⎧ Im ⎨ E i ( t ) ⎩ ∞ ∫ h1111 ( τ )Ei ( t – τ ) ( e 0 (6b) – i ( ω i – ω l )τ ∗ dτ ) ⎫ ⎬dt ⎭ OPTICAL FIBER CWDM ⎛ Number of PS ( PN ) ⎞ dN m ---------- = – 2α m N m + 2ργ m N m Im ⎜ ∑ Rmh Ph⎟⎠ + dz ⎝ h=1 2ργ m N m -------------------T.W. Number of SS T.W. ∑ i=1 ∫ 0 ⎧ Im ⎨ E i ( t ) ⎩ ∞ ∫ h1111( τ )Ei ( t – τ ) ( e 0 – i ( ω i – ω m )τ (6c) ∗ dτ ) ⎫ ⎬dt ⎭ In Equation (6), the time window size is denoted by T.W., and the star symbol means complex conjugation. The first three terms in the R.H.S of Equation (6a) are the SPM and XPM caused by the rest of the sampled signals and the parameterized signals on the i -th sampled signal. The fourth term is responsible for the SRS induced energy exchange between the i -th sampled signal and all the other sampled signals. The fifth term takes into account the energy exchange between the i -th sampled signal and all the parameterized signals. The last (sixth) term describes the SPM and XPM stemming from the delayed nonlinear response of the material. This effects can be turned on and off by the "Molecular SPM and XPM" parameter. The fourth and fifth terms (responsible for the SRS induced energy exchange between the sampled signals and the parameterized signals, respectively, are simultaneously switched on by setting the "Complete Raman response" parameter to TRUE. The sets contained in Equations (6b) and (6c) describe the evolution with propagation of the parameterized signals powers and noise bins powers respectively. The physical meaning of the terms in the RHS of Equations (6b) and (6c) is the following: The first terms take into account the attenuation. The second terms describe the energy exchange with parameterized signals due to SRS effect. These two terms are included in the simulation by switching on the "Complete Raman response" parameter. The last terms in the sets of Equations (6b) and (6c) describe the interaction of parameterized signals with sampled signals and of that of noise bins with sampled signals respectively. { E i } do not change significantly over the characteristic Raman response time of the medium, E i ( t – τ ) can be replaced with E i ( t ) in the In case the field envelopes integrands in Equations (6a), (6b) and (6c). Using h 1111 ( ω i – ω m ) = ∞ ∫ h1111 ( τ )e – i ⟨ ω i – ω m⟩ τ dτ , 0 the set of Equations (6) reduces to its simplified version, the set of Equations (1). 317 OPTICAL FIBER CWDM Vector approach Signal propagation equations When the polarization state of the incident sampled signals is not preserved during its propagation inside the optical fiber the scalar approach is no longer applicable and (1) is replaced by ("Model type" parameter must set to "Vector"). 2 ∂E iX ∂E iX iβ 2 ( ω i ) ∂ E iX _ ----------- + ( β 1X ( ω i ) – β 1 ( ω 0 ) ) ---------- + α ( ω i )E iX + ----------------- ------------2 ∂z ∂T 2 ∂T 3 β 3 ( ω i ) ∂ E iX ---------------- ------------- = iγi 2 3 6 ∂T Number of SS ∑ k=1 EkX – E iX + 2--3 2 2 Number of SS ∑ E kY (7a) 2 E iX k=1 2 ∂E iY ∂EiY iβ 2 ( ω i ) ∂ E iY _ ---------- + ( β 1Y ( ω i ) – β 1 ( ω 0 ) ) ---------- + α ( ω i )EiY + ----------------- ------------2 ∂z ∂T 2 ∂T 3 β 3 ( ω i ) ∂ E iY ---------------- ------------- = iγ i 2 3 6 ∂T Number of SS ∑ k=1 E kY – E iY + 2--3 2 2 Number of SS ∑ EkX (7b) 2 E iY k=1 SRS is disabled automatically when the vector model is selected and noise bins and PS are just attenuated. The nonlinear terms in (7a) and (7b) contain SPM, XPM between parallel polarization components, and XPM between orthogonal polarization components. If the parameter "XPM" is set to TRUE, both XPM contributions (between parallel and between orthogonal polarization components) will be included. If "XPM" is set to FALSE, only the nonlinear contributions of SPM will included in the model. Note that the group delays are different for the two polarization components of the same sampled band which takes into account the birefringence. The birefringence can be two types: "Deterministic" and "Stochastic". In the first case, the birefringence is assumed constant and no energy exchange between the two polarization components occurs. In the second case, ("Stochastic" birefringence) random mode coupling is also enabled, which gives the possibility to simulate PMD (see the technical description of Nonlinear Dispersive Fiber Total Field for the details 318 OPTICAL FIBER CWDM of the PMD simulator). It should be kept in mind however that when the signals are represented as multiple sampled bands PMD impairments will be identical for all WDM channels. To obtain the frequency dependence of the penalties (or Q-factors) total field approach must be implemented by setting "Merge sample bands" to true. Numerical solution The symmetrized non-iterative split-step Fourier method [1] (see the technical description of Nonlinear Dispersive Fiber Total Field) is used to solve Equations (1a), (6a), and (7a, b). These equations are first rewritten in normalized (dimensionless) quantities in the following way: The time variable is divided by the time window size. "Averaged" GVD coefficient is introduced by averaging over the entire set of sampled signals. This averaged GVD coefficient and the actual time window size are then used to define the characteristic dispersion length [1] and this value normalizes the longitudinal variable (z). The maximum peak power for SS is determined as the global maximum over the time window and the entire set of SS. This value is compared with the maximum power over the set of PS. The quantity that is bigger is used to normalize the waveforms of the SS and the powers of the PS. The characteristic nonlinear length is defined by the averaging the nonlinear lengths of all PS and SS. The solution is advanced from z to z + h . h is the step-size, determined from the value of the Max. nonlinear phase shift parameter according to: ⎛ E ( z + h, T ) = exp ⎛ h--- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝ where the z+h ∫ z ⎞ N̂ ( z' ) dz'⎟ exp ⎛ h--- D̂⎞ E ( z, t ) ⎝2 ⎠ ⎠ (8) D̂ is the dispersion and N̂ are the nonlinearity operators [1],[9]. Dispersion operator is applied in the frequency domain using FFT. The approximation: z+h ∫ N̂ ( z' ) dz' ≈ hN̂ ( exp [ ( h ⁄ 2 )D̂ ]E ( z, t ) ) (9) z 319 OPTICAL FIBER CWDM is used. When the "Step size" parameter is set to "Constant" (7) can be simplified according to: ⎛ h E ( z + 2h, t ) = exp ⎛ --- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝ ⎛ h exp ⎛ --- D̂⎞ exp ⎜ ⎝2 ⎠ ⎝ z+h ∫ z z+h ∫ z ⎞ h h ⎛ N̂ ( z' ) dz'⎟ exp ⎛ --- D̂⎞ exp ⎛ --- D̂⎞ ⎜ ⎝ ⎠ ⎝ 2 2 ⎠⎝ ⎠ ⎞ ⎛ N̂ ( z' ) dz'⎟ exp ( hD̂ ) exp ⎜ ⎠ ⎝ z+h ∫ z z+h ∫ z ⎞ h N̂ ( z' ) dz'⎟ exp ⎛ --- D̂⎞ E ( z, t ) = ⎝2 ⎠ ⎠ (10) ⎞ h N̂ ( z' ) dz'⎟ exp ⎛ --- D̂⎞ E ( z, t ) ⎝2 ⎠ ⎠ which is executed faster. In the presence of attenuation, however, the role of nonlinearity will decrease along the fiber length and "Variable" step size will be advantageous. When the system (6) is solved (the parameter "Complete Raman response" is set to TRUE), the second order Runge-Kutta scheme is used to apply the nonlinearity operator. References: [1] G. P. Agrawal, "Applications of nonlinear fiber optics", Academic press, 3rd edition, 2001. [2] G. P. Agrawal, "Nonlinear fiber optics", Academic press, 3rd edition, 2001. [3] R. W. Hellwarth, Prog. Quant. Electr. 5, 1 (1977). [4] P. Tchofo Dinda, G. Millot, and S. Wabnitz, JOSA B, 15, 1433, (1998). [5] R.H.Stolen, J.P.Gordon, W.J. Tomlinson and H.A. Haus, JOSA B, 6, 1159 (1989). [6] C.R.Menyuk, M.N.Islam and J.P.Gordon, Optics Letters, 16 566, (1991). [7] K.J. Blow and D. Wood, IEEE J. Quant. Electr., 25, 2665, (1989). [8] W. H. Press, et al., "Numerical Recipes: The Art of Scientific Computing", 2nd Edition, Cambridge University Press, 1992. [9] M. Lax, J. H. Batteh and G. P. Agrawal, Journ. Appl. Phys. 52 , 109, (1981). 320 BIDIRECTIONAL OPTICAL FIBER Bidirectional Optical Fiber The component simulates the bidirectional propagation of arbitrary configuration of optical signals in a single-mode fiber. Dispersive and nonlinear - self-phase modulation (SPM), cross-phase modulation (XPM), stimulated Raman (SRS) and Brillouin (SBS) scattering effects - are taken into account. Raman interaction for an arbitrary configuration of sampled and parameterized signals is also considered. The component provides most of the functionality of the total field approach fiber model (except for the simulation of the Raman effect in birefringent fibers). The four-wave mixing effect between multiple sampled signals is not considered. Ports Name and description Port type Signal type Input1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical 321 BIDIRECTIONAL OPTICAL FIBER Parameters Main Name and description Symbol User-defined reference wavelength Default value Units True Value range [True, False] If True, the frequency corresponding to the value entered under "Reference wavelength" is used internally as reference frequency. The system of modified NLS equations governing the evolution of the signals is solved in a frame moving with the group velocity corresponding to that frequency. If False, the value of the reference frequency is calculated as the averaged of the central frequencies of all the sampled and parameterized signals. Reference wavelength λ0 1550 nm [100, 2000] L 50 km [0, 100000] The value of the user-specified reference wavelength Length Fiber length Attenuation effect True [True, False] Constant [Constant, From file] If True, the attenuation effect is enabled Attenuation data type Defines if the attenuation value will be read from the "Attenuation" tab or from a file. If "Constant", the value specified in the "attenuation" tab will be used for all sampled, parameterized signals and noise bins. If "From file", a separate value will be calculated for each noise bin, parameterized or sampled signal by interpolating the data file. Attenuation The specified value will be used for all signals if "Attenuation data type" is set to "Constant". If "Attenuation data type" is set to "From file", the value will be ignored. 322 α 0.2 dB/km [0, 1010] BIDIRECTIONAL OPTICAL FIBER Name and description Symbol Default value Units Value range Symbol Default value Units Value range Attenuation vs. wavelength If "Attenuation data type" is set to "From file", this field specifies the file containing the attenuation data. In this case the attenuation effect is wavelength dependent for all types of signals. Values corresponding to the central frequency of each signal will be calculated by linear interpolation and used internally. Dispersion Name and description Group velocity dispersion True [True, False] True [True, False] If True, the GVD effect is enabled Third order dispersion If True, the TOD effect is enabled Dispersion data type Constant [Constant, From file] Defines if the dispersion parameter values will be read from the tabs or from a file. If "Constant", the values from the tabs will be used to calculate the relative group delay and the first-order GVD for each sampled signal by Taylor expansion around the reference wavelength. If the parameter is set to "From file", the group delay, and the first- and second-order GVD parameters corresponding to each sampled signal will be calculated from the userspecified file by Sellmeier fitting. When "Frequency domain parameters" is True, "Dispersion data type" will remain "Constant" and cannot be changed. This is done because the only acceptable format for the file specifying the dispersion is group delay vs. wavelength. Frequency domain parameters False [True, False] Defines the domain in which the dispersion parameters are specified. If True, the frequency domain is used and the dispersion effect is specified in terms of β 2 and β 3 . Otherwise the wavelength domain is used (D and S). This parameter is meaningful (that is, enabled) only if "Dispersion data type" is set to "Constant". 323 BIDIRECTIONAL OPTICAL FIBER Name and description Symbol Default value Units Value range Beta 2 D 16.75 ps/[(nm)(km)] [-10100, 10100] 0.75 ps/[(nm)2(km)] [-10100, 10100] β2 -20 ps2/km [-10100, 10100] β3 0 ps3/km [-10100, 10100] The value of the GVD parameter in the frequency domain Beta 3 The value of the TOD parameter in the frequency domain Dispersion The value of the GVD parameter in the wavelength domain Dispersion slope The value of the dispersion slope parameter in the wavelength Dispersion file name Specifies the file with the dispersion data Note: The notation "Frequency domain parameters" refers to these alternative definitions: Wavelength domain definition: ∂β ∂DD = --------1- , S = -----∂λ ∂λ Frequency domain definition: ∂β ∂β β 2 = --------1- , β 3 = --------2∂ω ∂ω However, the format of the file specifying the wavelength dependence of the dispersion is the following: • • (λ) the second column contains the corresponding values of ( λ ) the first column of the file contains wavelength values Consequently, the "Frequency domain parameters" is meaningless when the dispersion is specified from a file. 324 BIDIRECTIONAL OPTICAL FIBER PMD Name and description Symbol Birefringence type Default value Units Deterministic [Deterministic, Stochastic] Determines the type of birefringence. If "Deterministic" is selected, both the strength of birefringence and principal axes are assumed constant. Therefore, the random mode coupling is disabled. If "Stochastic" is selected, the random mode coupling is enabled. Differential group delay If "Birefringence type" is set to "Deterministic", this is the value of the differential group delay. If "Birefringence type" is set to "Stochastic", the parameter is disabled. PMD coefficient d - ( Δβ ) -----dω 0 ps/km [-10100, 10100] DP 0, 5 ps ---------km [0, 10100] L scatt 500 m [0, 10100] σ scatt 100 m [0, 10100] If "Birefringence type" is set to "Stochastic", this is the value of the PMD parameter. If "Birefringence type" is set to "Deterministic", the parameter is disabled. Mean scattering section length Value range The averaged value of the fiber length at which the polarization states of the signal is randomized by applying the scattering matrix. Scattering section dispersion The dispersion of the scattering section length In the case when more than one sampled signal (separated channels) is propagating in the fiber, the PMD-induced penalties will be the same for all channels. Different penalties (and Q-factors) will be obtained if all the channels are merged (total filed approach). Birefringence and random mode coupling do not affect parameterized signals and noise bins. Nonlinearities Name and description Self-phase modulation Symbol Default value True Units Value range [True, False] Determines if the self-phase modulation (SPM) effect will be taken into account. If False, all the nonlinear effects (XPM, SRS) will be disabled. 325 BIDIRECTIONAL OPTICAL FIBER Name and description Symbol Cross-phase modulation Default value Units Value range True [True, False] Constant [Constant, From file] Determines if the XPM effects are taken into account. The parameter is active if the SPM effects are enabled. In the scalar case, XPM includes the interactions among all parameterized and sampled signals. In the vector case, only interactions between sampled signals are considered. The XPM between orthogonal polarization components is included. Effective area data type Defines if the effective area parameter value will be read from the tab or from a file. If "Constant", the value from the tab will be used. Otherwise, the parameter is treated as wavelength dependent and a separate value corresponding to the center frequency of each sampled signal. The parameterized signal and noise bin are calculated and used. Effective area A eff 80 The value of the effective area parameter. This value will be used if "Effective area data type" is set to "Constant". Otherwise the value will be ignored. μm 2 [0, 1010] Effective area vs. wavelength If the "Effective area data type" is set to "From file", this tab specifies the file containing the effective area data. n2 data type Constant [Constant, From file] Defines if the n2 parameter value (nonlinear index of refraction) will be read from the tab or from a file. If "Constant", the value from the tab will be used. n2 n2 The value of the n2 parameter. If "n2 data type" is set to "Constant", this value will be used. Otherwise it will be ignored. n2 vs. wavelength If the "n2 data type" is set to "From file", this tab specifies the file containing the nonlinear index of refraction wavelength data. 326 2.6 x 10-20 m2/W [0, 10100] BIDIRECTIONAL OPTICAL FIBER Name and description Symbol Raman scattering Default value Units Value range False [True, False] 0.18 [0, 1] Raman gain [Raman gain, Raman gain efficiency, Calculate] 1e-013 [0, +INF] Interactions among all sampled signals, parameterized signals and noise bins are considered. Noise bins are treated as a weak probe with respect to the sampled signals and parameterized signals - the latter are treated as pumps. Inter-band Raman scattering [1-7] is an approximation to the full expression of the Raman polarization valid provided that the frequency separation of the interacting signals is much larger than their individual spectral bandwidths. SRS effect can be enabled only in the scalar case (fixed polarization state, "Model type" from the numerical tab should be set to "Scalar" to enable SRS) Fractional Raman contribution ρ The fraction of the nonlinear polarization, related to the stimulated Raman scattering effect [1] Raman gain type Defines type of Raman gain. If Raman gain efficiency is selected, then its value is gr/Aeff, otherwise, it is normalized gr multiplied by Raman gain peak. There is the option to calculated the Raman gain based on fiber parameters Raman gain peak Normailized Raman gain is multiplied by Raman gain peak. Raman gain reference pump 1000 nm gr RG.dat THz - normalized Raman Gain or THz - Raman Gain T 300 K Keff 2 [0, +INF] Value used in the Raman gain calculation Gain X frequency File that defines the Raman gain or the Raman gain efficiency. Temperature [0, 500] Absolute temperature at wich the fiber is operating. Used for noise consideration. Polarization factor [1, 2] The value depends on the relative polarization of the fields. The value is 1 if the the fields have aligned polarizations, and 2 if they have scrambled polarization. 327 BIDIRECTIONAL OPTICAL FIBER Enhanced Name and description Symbol Rayleigh scattering Default value Units Value range False True, False Constant [Constant, From file] Defines if the Rayleigh scattering effect is enabled Rayleigh data type Defines if the Rayleigh parameter value will be read from the tab or from a file. If "Constant", the value from the tab will be used Rayleigh backscattering γ 5.0e-005 1/km Rayleigh.dat nm - 1/km [0, +INF] The value of the γ parameter. If "Rayleigh data type" is set to "Constant", this value will be used. Otherwise it will be ignored Rayleigh vs. wavelength If the "Rayleigh data type" is set to "From file", this tab specifies the file containing the Rayleigh wavelength data Include Brillouin scattering False True, False Constant [Constant, From file] Determines if the Brillouin scattering effect will be taken into account Brillouin gain data type Defines if the Brillouin gain is constant or loaded from a file Brillouin gain constant gB 4.6e-11 m/W [0, 1e10] Brillouin gain value Brillouin.dat Brillouin gain file name Specifies the Brillouin gain file name Brillouin linewidth Δv 31.7 MHz [-INF, +INF] vs 11 GHz [-INF, +INF] Specifies the Brillouin linewidth Frequency shift Specifies the Brillouin frequency shift 328 BIDIRECTIONAL OPTICAL FIBER Numerical Name and description Model type Symbol Default value Units Value range Scalar [Scalar, Vector] Variable [Variable, Constant] Defines the model type used for the simulation depending on the polarization state of the signal. If "Vector" is selected, the signal can have arbitrary polarization state and a system of two coupled equations, corresponding to each polarization component (x or y) of every sampled signal that is solved. If "Scalar" is selected, all the signals preserve their polarization state and a single equation (1) is solved for each sampled band. Vector simulation will be performed, regardless of the value of the model type parameter, in the following two cases 1)Two polarization components are detected at the fiber input. This will work for sampled noise because the noise is unpolarized and x- and y-polarization components are stored independently in the memory. However, sampled signals with well defined polarization state might use a different method of storage in the memory. Consequently, this parameter should be manually set to "Vector" if the polarization evolution is to be considered. 2)The PMD effect is set to Stochastic. Turning the "vector" on will disable SRS. Step size Specifies whether variable or fixed stepsize simulation will be used. If "Variable" is selected, the step size is adaptively changed depending on the value of the "Max. nonlinear phase shift" parameter and the behavior of solutions itself. Otherwise the step size is evaluated only once, at the beginning of the simulation. In some cases, the fixed step size calculation executes faster, due to the smaller number of calculations per step. However, the variable step size calculation is more flexible and can be faster in the presence of strong attenuation. 329 BIDIRECTIONAL OPTICAL FIBER Name and description Max. nonlinear phase shift Maximum phase shift (over the time window) induced by the self-phase modulation effect per step is calculated for each sampled signal. SPM-induced phase shifts are then calculated for each parameterized signal. Next, the step size is calculated in such a way that the maximum SPM-induced phase shift (over the entire set of signals) is equal to the specified value. Symbol Default value Units Value range 3 [0, 10100] Periodic [Periodic, Absorbing] 0.5 [0, 10100] 50 [1, 1000] 40 [1, 1000] 1e-3 [1e-10, 1] NL ϕ max Boundary conditions Specifies the type of boundary conditions used for the simulation Filter steepness When "Boundary conditions" option is set to "Absorbing", the "Filter steepness" parameter determines the absorption and reflection properties of the time window boundaries. The same absorbing boundary conditions are used for all sampled signals. P. A. number of iterations Maximum number of iterations executed in the Power Analysis. If convergence is not reached in this number of iterations, model returns the calculated values anyway P. A. number of steps Number of divisions (in space) of the fiber P. A. relative tolerance Used to check the convergence of the signal Discretize sampled signal False — — True, False 100 GHz Hz, GHz, THz [1e9,1e12] 0.001 — — [1e-100, 1e100] Defines whether to use a user defined discretization for sampled signals or not Frequency resolution Frequency spacing that will discretize the sampled signal P. A. step accuracy 330 BIDIRECTIONAL OPTICAL FIBER Graphs Name and description Calculate graphs Symbol Default value Units Value range False [True, False] 200 [1, 100000000] 200 [1, 100000000] True [True, False] Wavelength range [Wavelength range, One sampled signal] Defines whether to enable the 3D graphs. If disabled, no graphs will be plotted and no data is stored. Graphs are plotted for sampled signals only. Number of distance steps The number of longitudinal (or in z) snapshots (slices) that will be used to construct a 3D plot. Increasing this value will make the 3D graph look better. The number of snapshots that are stored cannot be larger than the number of steps in z taken by the simulation to obtain the solution. The latter is determined by the maximum nonlinear phase-shift parameter (numerical tab). Number of wavelength/time steps The number of stored points (in t) per snapshot. Increasing this value will make the 3D graph look better. Linear scale Determines the axis-type (linear or logarithmic) for the dependent variable. If True, the axis type is linear. The next six parameters in this tab determine which graphs will be plotted after the simulation is finished. Plot type Determines the type of the plot that will be created in either frequency or time domain. If the parameter is set to "Wavelength range", a copy of each sampled signal residing in the specified wavelength range will be created. These copies will be up-sampled and merged in a single frequency band. This single frequency band, containing all the signals, will be plotted in either frequency or time domain. The merging does not affect the original signals but affects their copies. Therefore, multiple sampled signals will be involved in the simulation. If the parameter is set to "Plot one sampled signal", a 3D graph presenting the sampled signal with central frequency given by "Signal center frequency" will be created. 331 BIDIRECTIONAL OPTICAL FIBER Simulation Name and description Default value Default value Enabled Units True Value range [True, False] Determines whether the component is enabled. If False, all the input signals reach the output port of the component without any change. Noise Name and description Default value Convert noise bins Default value Units False Value range [True, False] If True, each noise bin in the bandwidth of the signal will be converted to a Gaussian white noise, with the correct power spectral density, This noise will be added to the signal. Random numbers Name and description Generate random seed Default value Default value Units Value range True [True, False] 0 [0, 4999] Determines how the random number generator is initialized (seeded). If True, the seed index used for this initialization is a random number. Otherwise, a userspecified number is used for this purpose. Random seed index If "Generate random seed" is set to True, this value specifies the seed index. The generated pseudo-random sequence is the same one if the seed index is not changed. The value of "Random seed index" will be ignored if "Generate random seed" is set to True. Technical Background Numerical Solution To model the bidirectional signal propagation in a fiber, an algorithm that takes two numerical steps is used [1]. • 332 In the first step, the equations describing the signal propagation in the forward and backward direction are solved by an iterative method (Power analysis) and the power distribution along the fiber is calculated. BIDIRECTIONAL OPTICAL FIBER • In the second step, the signals are propagated using the nonlinear Schrödinger equation to describe the dynamic interactions between the co-propagating signals. Power Analysis The equations that describe the interactions between signals propagating in the forward direction and backward direction and describe the generation of optical noise due the Raman and Rayleigh scattering are defined by [2]: 333 BIDIRECTIONAL OPTICAL FIBER where v i, v j are frequencies α(v) is the fiber attenuation γ( v) is the Rayleigh backscattering coefficient g γ ( v i – v j ) is the Raman gain coefficient for frequency difference ( v i – v j ) P b (Z,v) is the backward propagating power. It includes sampled, parameterized, and noise bins signals. A eff is the effective core area K eff is the polarization factor Δv is the frequency interval h is Plank's constant k is the Boltzman's constant T is the absolute temperature. In these equations, the following physical effects were taken into account: a) pump-to-pump, signal-to-signal and pump-to-signal Raman interactions b) spontaneous Raman emission and its temperature dependency c) stimulated Raman scattering d) pump depletions due to Raman energy transfer e) high-order stokes generation f) multiple Rayleigh backscattering g) fiber loss h) spontaneous emission noise In the first solution step in this component, the equations (1) (forward and backward) are solved through direct integration. In direct integration, the signal launch configuration defines the boundary conditions in both ends of the fiber. The convergence of the model is checked in two directions: forward and backward. An iterative forward and backward integration of propagation equations must be used due to the backward propagating ASE powers and counter-directional pumping scheme that may be defined, as well as the possibility of counter directional signal propagation [2]. The forward direction is from input port 1 to output port 1. The backward direction is from input port 2 to output port 2. The convergence is checked after the integration in both directions is performed. If the variance in the gain is lesser than the tolerance desired ("Numerical" tab page), the simulation is considered finished. Otherwise, the component runs for the maximum number of iterations set by the user. 334 BIDIRECTIONAL OPTICAL FIBER When a file with the normalized Raman gain is entered, it must be given values for the Raman gain peak and Raman gain reference pump. These values are used to calculate the Raman gain used in the simulation according the following formula: where gR is the Raman gain pR is the Raman gain peak λP is the gain reference pump gN is the normalized Raman Gain. The unit of Raman Gain is given in m⁄W . If the user chooses the option to let the component calculate the Raman gain, the component will calculate the coefficients using the following equation: where γ is the nonlinear coefficient (6) ρ is the fractional Raman contribution R X 1111 ( ω P – ω S ) is the Raman susceptibility for fused silica Stimulated Brillouin scattering When the stimulated Brillouin scattering (SBS) effect is included in the simulation. New terms and equations are added to the set of coupled equations, and they are related to the stokes signals introduced in the system. The modeling of SBS used here is based on reference [7] and it can not be used together with Raman amplification. After the calculation of the power distribution along the fiber for the signals, spontaneous emission and Rayleigh scattering, the dynamic interaction between the co-propagating signals are analyzed using the nonlinear Schrödinger equations 335 BIDIRECTIONAL OPTICAL FIBER Nonlinear Schrödinger Equation In this step, the coupled nonlinear Schrödinger equations are solved by using the symmetrized non-iterative split-step Fourier method. See the Optical Fiber WDM Technical Background. Scalar approach Signal propagation equations with Raman scattering In the scalar approach, the optical field maintains its polarization along the fiber length. The Model type parameter from the "Numerical" tab is set to Scalar. In this case, the following set (4) of equations governs the evolution of the slowly varying electric field envelopes (Ei). These envelopes are a set of sampled signals (SS), powers (Pl) of another set of parameterized signals (PS), and powers (Nm) of a third set of noise bins (NB). The subsystem (4a) consists of • Number of SS, the total count of sampled signals • coupled nonlinear Schrödinger (NLS) [3, 4], The subsystem (4b) contains • 336 Number of PS equations (the total count of PS) BIDIRECTIONAL OPTICAL FIBER The subsystem (4c) contains • Number of NB (the total count of NB) equations. The Raman matrices are defined according to: 337 BIDIRECTIONAL OPTICAL FIBER Raman susceptibility for fused quartz is shown in Figure 1. It should be noted that "*" means complex conjugation. Figure 1 Raman susceptibilities for fused silica [5, 6] In Equation (4a), signal. E i = E i (z,T) is the electric field envelope of the i-th sampled A frame moving at the group velocity ( T = the reference frequency ω 0 is assumed. 338 t – z ⁄ vg ≡ t – β 1 ( ω 0 )z ) corresponding to BIDIRECTIONAL OPTICAL FIBER The reference frequency is related to the parameter Reference wavelength through ω 0 = 2πc ⁄ λ 0 , with c being the light speed in vacuum. The parameter Reference wavelength is in the "Main" category of the component tool-box. The derivatives of the propagation constant of the fiber mode β ( ω ) , with respect to n n frequency β n = ∂ β ( ω ) ⁄ ( ∂ω ) n = 1, 2 are the first order β 2 and second order β 3 group velocity dispersion (GVD) parameters and are evaluated at the center frequencies { ω i } of the sampled signals. The nonlinear coefficients for every SS, NB or PS in (4) are defined according to The meaning of the terms in the left-hand side of the subsystem (4a) is the same as in the total field approach fiber model (see the technical description of this component). The first two terms in the right side of (4a) give the SPM and XPM contributions of the remaining sampled signals. The third term is the XPM contribution of the PS. The fourth and the fifth terms describe the SRS-induced interactions between the i-th sampled signal and rest of the sampled signals and with the parameterized signals, respectively. Subsystems (4b) and (4c) describe the power balance of the set of PS and NB, respectively. These are obtained by replacing the NLS equations for NB and PS with the time-averaged versions of their power conservation laws. In the absence of attenuation, the total number of photons is conserved as (4) shows. The first terms in the right sides of (4b) and (4c) take into account the attenuation effects. The second and the third terms in the right side of (4b) describe the SRS induced power transfer between the l-th PS and the rest of the PS and between the lth PS and the SS, respectively. The second and the third terms in the right side of (4c) are responsible for the SRSinduced interactions between noise bins and PS and noise bins and SS. With multiple SS present in the fiber, the SRS effect is represented through inter-band Raman scattering. This is an approximation of the full expression for the Raman polarization [3,4] that is valid if the frequency separation between the interacting signals is large enough compared to their individual bandwidths. When the frequency separation between the signals is comparable with their individual spectral bandwidth, the total field approach can be implemented by turning on the option "Merge sampled bands". In this case, the system (4a) is replaced by the following single NLS equation (7) and (4b) and (4c) remain unchanged. 339 BIDIRECTIONAL OPTICAL FIBER In equation (7), the Raman response function the Raman susceptibilities shown in Figure 1. h 1111 ( t ) is the Fourier transform of Total field approach however should be used with some care. At first in this case (single sampled band), XPM and four wave mixing effects are included automatically in the simulation and turning on or off the XPM parameter in the "Nonlinearities" tab will have no effect on the results. Keep in mind that in the total field approach, all the parameters (such as dispersion and attenuation) are evaluated just once - at the reference frequency. In this case, when multiple SS are considered, a set of parameters is evaluated for each sampled signal - at the center frequency of the corresponding signal. The meaning of the reference frequency (and reference wavelength) is the following: The subsystem (4a) is written in a frame moving with group velocity corresponding to the reference wavelength. That is, no other signal parameters are evaluated at this frequency. The reference wavelength can be either user specified or automatic, which corresponds to the averaged frequency of the center frequencies of all SS and PS. If "Dispersion data type" is set to "Constant", the dispersion parameters specified in the tabs (D and S) or, respectively, β 2 and β 3 , are assumed to correspond to the reference wavelength. Hence, Taylor expansion is used in this case Evaluating (8) and its first and second derivatives with respect to ω at the signal frequencies { ω i } gives the sets of parameters β 1 ( ω ) – β 1 ( ω 0 ) }, { β 2 ( ω i ) } and { β 3 ( ω i ) } . It should be kept in mind, however, that with multiple sampled signals present, specifying nonzero β 2 and β 3 (or D and S) and at the same time disabling the "Group velocity dispersion" and "Third order dispersion", will result in { β 2 ( ω i ) = 0 ,∀i } , { β 3 ( ω i ) = 0 ,∀i } but { β 1 ( ω i ) ≠ β 1 ( ω j ), ifi ≠ j } . This means that no GVD-induced pulse broadening will be observed but pulses with different center frequencies will propagate with different group velocities. 340 BIDIRECTIONAL OPTICAL FIBER To the contrary, if all the sampled signals are merged to form a single frequency band, disabling the GVD effects will not only disable pulse broadening, but it also will set the group velocity constant for the entire sampled band considered. If "Dispersion data type" is set to "From file", the data set specified by the file is Sellmeier fitted. The dispersion parameters are calculated by analytically differentiating the fit. The file specifying the dispersion data must provide the dependence of group delay [ps/km] on the wavelength [nm]. For this reason, "Frequency domain parameters" is disabled when "Dispersion data type" is set to "From file". Vector approach When the polarization state of the incident sampled signals is not preserved during its propagation inside the optical fiber, the scalar approach is no longer applicable. A vector model is then selected and solved. The vector model is similar to the model presented in the Optical Fiber WDM (see Optical Fiber WDM Technical Background). In the same way, Raman scattering is not applied. References [1] J. Ko; S. Kim; J. Lee; S. Won; Y. S. Kim; J. Jeong, "Estimation of performance degradation of bidirectional WDM transmission systems due to Rayleigh backscattering and ASE noises using numerical and analytical models", IEEE J. of Lightwave Technology, Vol.: 21 , Issue: 4 , April 2003, Pag.:938 - 946 [2] M. Karasek, M. Menif, "Protection of surviving channels in pump-controlled gain-locked Raman fibre amplifier", Optics Communications 210 (2002) 57-65. [3] G. P. Agrawal, "Applications of nonlinear fiber optics", Academic press, 3rd edition, 2001. [4] G. P. Agrawal, "Nonlinear fiber optics", Academic press, 3rd edition, 2001. [5] R. W. Hellwarth, Prog. Quant. Electr. 5, 1 (1977). [6] P. Tchofo Dinda, G. Millot, and S. Wabnitz, JOSA B, 15, 1433, (1998). [7] A. backa, G. Jacobsen, and B. Tromborg, "Dynamic Stimulated Brillouin Scattering Analysis," J. Lightwave Technol. 18, 416- (2000) 341 BIDIRECTIONAL OPTICAL FIBER Notes: 342 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Nonlinear Dispersive Fiber (Obsolete) This component is an obsolete version that is included with OptiSystem for backwards compatibility purposes - It was replaced by the Optical Fiber component. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Length 50 km [0, INF] Constant — Constant, Wavelength Dependent/ From File 0.25 dB/km [0, INF] AtnVsLambda.dat — [0, INF] -1 dB [-INF,0] -0.022 dB [-INF,0] Fiber length Attenuation data type Defines the attenuation as a fixed constant value or as a wavelength dependent curve taken from a file Attenuation – constant Defines the attenuation as a fixed constant value, the same for all channels Attenuation vs. wavelength Defines the attenuation as a wavelength dependent curve in a file Input coupling loss Overall input coupling loss resulting from mode mismatch, Fresnel reflections, etc. Output coupling loss Overall output coupling loss resulting from mode mismatch, Fresnel reflections, etc. 343 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Dispersion Name and description Default value Default unit Value range Group delay data type Constant — Constant, Wavelength Dependent/ From File 4.9e+006 ps/km [-INF,INF] GroupVs Lambda.dat — [-INF,INF] Constant — Constant, Wavelength Dependent/ From File 4.5 ps/nm/km [-INF,INF] GVDvsLambda.dat — [-INF,INF] Constant — Constant, Wavelength Dependent/ From File 0.11 ps/nm2/km [-INF,INF] DispSlope vs. Lambda.dat — [-INF,INF] EffRIVsLambda.dat — [0,INF] Defines the group delay as a fixed constant value, or as a wavelength dependent curve taken from a file Group delay – constant Defines the group delay as a fixed constant value, the same for all channels Group delay vs. wavelength Defines the group delay as a wavelength dependent curve in a file GVD data type Defines the group-velocity dispersion as a fixed constant value, or as a wavelength dependent curve taken from a file GVD – constant Defines the group-velocity dispersion as a fixed constant value, the same for all channels GVD vs. wavelength Defines the group-velocity dispersion as a wavelength dependent curve in a file Dispersion slope data type Defines the dispersion slope as a fixed constant value, or as a wavelength dependent curve taken from a file Dispersion slope – constant Defines the dispersion slope as a fixed constant value, the same for all channels Dispersion slope vs. wavelength Defines the dispersion slope as a wavelength dependent curve in a file Effective refractive index vs. wavelength Defines the effective refractive index as a dispersive curve vs. the wavelength in a file 344 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Birefringence Name and description Default value Default unit Value range Birefringence data type Constant — Constant, Wavelength Dependent/ From File 6.2832e-005 rad/m [-1,1] BirefringenceVs Lambda.dat — [-1,1] 0.1 km [0,INF] 0.07 ps/km1/2 [0,INF] Constant — Constant, Wavelength Dependent/ From File 3 ps/km [-INF,INF] DGDVsLambda.dat — [-INF,INF] Defines the birefringence (the mismatch between the propagation constants of the two orthogonal polarization modes) as a fixed constant value, or as a wavelength dependent curve taken from a file Birefringence – constant Defines the birefringence as a fixed constant value, the same for all channels Birefringence vs. wavelength Defines the birefringence as a wavelength dependent curve in a file Coupling length of polarization mixing Coupling length of polarization scrambling PMD coefficient Polarization mode dispersion coefficient DGD data type Defines the differential group delay between the two orthogonal polarization modes as a fixed constant value, or as a wavelength dependent curve taken from a file DGD – constant Defines the differential group delay as a fixed constant value, the same for all channels DGD vs. wavelength Defines the differential group delay as a wavelength dependent curve in a file 345 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Nonlinearities Name and description Default value Default unit Value range Effective area data type Constant — Constant, Wavelength Dependent/ From File 72 μ2 [0,INF] EffAreaVsLambda.dat — [0,INF] Constant — Constant, Wavelength Dependent/ From File 2.6e-020 m2/W [-INF,INF] N2VsLambda.dat — [-INF,INF] RamanResN2Vs Freq.dat — [-INF,INF] 9.9e-014 m/W [0,INF] 1000 nm [0,INF] RamanGainVsFreq.dat — [0,INF] 5 fsec [0,INF] Defines the effective area of the fiber as a fixed constant value, or as a wavelength dependent curve taken from a file. Effective area – constant Defines the effective area as a fixed constant value, the same for all channels. Effective area vs. wavelength Defines the effective area as a wavelength dependent curve in a file. n2 data type Defines the nonlinear refractive index as a fixed constant value, or as a wavelength dependent curve taken from a file. n2 – constant Define the nonlinear refractive index as a fixed constant value, the same for all channels. n2 vs. wavelength Defines the nonlinear refractive index as a fixed constant value, or as a wavelength dependent curve taken from a file. Raman-resonant n2 dispersion Defines the Raman-resonant dispersion of the thirdorder nonlinear susceptibility as a frequency dependent curve in a file Peak Raman gain coef The peak Raman gain coefficient at certain pump wavelength Pump Wavelength of Peak Raman gain coef The pump wavelength corresponding to the above peak Raman gain coefficient Raman Gain Spectrum Defines the Raman gain spectrum vs. frequency in a file Raman self-shift Time The characteristic Raman self-frequency shifting time 346 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Effects On/Off; Model Details Name and description Default value Default unit Value range Attenuation ON — [ON, OFF] ON — [ON, OFF] ON — [ON, OFF] ON — [ON, OFF] Hi-Bi PM fiber, no PMD, fixed DGD — Hi-Bi PM fiber, no PMD, fixed DGD, Non-PM fiber, PMD, stochastic DGD, Averaged polarizations Switch On/Off the attenuation Group velocities mismatch Switch On/Off the group velocities mismatch GVD (Group velocity dispersion) Switch On/Off the group velocity dispersion GVD Slope (third-order dispersion) Switch On/Off the dispersion slope (the third-order dispersion) Polarization evolution Specify the polarization maintaining capabilities of the fiber and the polarization evolution models to use Independent pol. mode mixing of WDM channels OFF [ON, OFF] In the case of non-PM fiber, determines whether the polarization scrambling follows the same pattern for all the channels or is completely independent n2 polarization factor 1 dimensionless [0.5, 1] Raman Gain polarization factor 1 dimensionless [0.5, 1] Birefringence ON — [ON, OFF] ON — [ON, OFF] ON — [ON, OFF] ON — [ON, OFF] OFF — [ON, OFF] OFF — [ON, OFF] 100 radian [-1e+100, 1e+100] Switch On/Off the birefringence SPM (Self-phase modulation) Switch On/Off the SPM (Self-phase modulation) XPM (Cross-phase modulation) Switch On/Off the XPM (Cross-phase modulation) XPM of orthogonally polarized modes Switch On/Off the XPM of orthogonally polarized modes FWM (four-wave mixing) Switch On/Off the FWM (four-wave mixing) FWM of orthogonally polarized modes Switch On/Off the XPM of orthogonally polarized modes Maximal phase-mismatch FWM generated waves with phase-mismatches larger than this value are neglected 347 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Name and description Default value Default unit Value range SRS (stimulated Raman scattering) ON — [ON, OFF] SRS with pump wave depletion ON — [ON, OFF] OFF — [ON, OFF] Name and description Default value Default unit Value range Enabled ON — [ON, OFF] 25 — [0,INF] Fixed = Main Channel Initial Nonlinear length/Number of Steps — Fixed = Full length/Number of Steps Switch On/Off the effect of pump wave depletion in SRS RSFS (Raman self-frequency shifting) Switch On/Off the RSFS (Raman self-frequency shifting) Simulation Enable the calculations Number of steps Number of longitudinal steps Step defined as: Choose one of the three alternative ways of defining the step size Fixed = Main Channel Initial Nonlinear length/Number of Steps Variable = Main Channel Current Nonlinear length/Number of Steps Time-window boundaries Absorbing — Periodic, Absorbing OFF — [ON,OFF] 1 — [0, 65535] Choose the type of the time-window boundary conditions Random Phases Randomize the phase offsets of the channels at input Random Phases Seed The seed of the random phases 348 NONLINEAR DISPERSIVE FIBER (OBSOLETE) 3D graphics selection Name and description Default value Default unit Value range Power spectrum of channels OFF — [ON,OFF] dBm — mW, dBm OFF — [ON,OFF] ON — [ON,OFF] 0 nm [0,INF] ON — [ON,OFF] OFF — [ON,OFF] OFF — [ON,OFF] OFF — [ON,OFF] 50 — [2, 1000] Displays the average power spectrum of the channels Unit of power spectra Displays the average power spectrum of channels or the PSD of a selected channel in [mW] or [dBm] Bandwidth spectrum of channels Displays the rms bandwidths of the channels Monitor central sampled channel Monitors the center most channel if described as a sampled waveform Wavelength of sampled channel to monitor Monitors an arbitrary sampled channel, defined by its central wavelength Waveform Displays the waveform of the selected sampled channel Chirp Displays the chirp of the selected sampled channel PSD Displays the PSD of the selected sampled channel Spectral Delay Displays the spectral delay of the selected sampled channel Number of 2D snapshots in the 3D graphics Defines the number of 2D snapshots forming the selected 3D graphics Graphs Name and description X Title Y Title Fiber 3D Graph EmptyX EmptyY 349 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Parameters—Detailed descriptions In the following section, the parameters descriptions are further elaborated. There are descriptions of features pertaining to multiple parameters, and also extended descriptions of individual parameters. Note: Many parameters pertaining to the NDF can be defined as either constant or wavelength dependent/from file values. The first option is used usually for rapid development of simple designs. If a parameter is wavelength dependent (arb. curve ) you have to prepare a text file with (Wavelength ParameterValue) data pairs, and create the parameter in the appropriate Component properties dialog box. This option is recommended for detailed, quantitatively precise designs. Many parameters of the NDF, such as losses, dispersion, and effective fiber area, can be defined in both ways - as constants or curves loaded from a file. When a parameter is defined as a curve, the format of the text file is as follows: Wavelength_1 ParameterValue_1 Wavelength_2 ParameterValue_2 Wavelength_3 ParameterValue_3 ...... Wavelength_N ParameterValue_N The units of wavelength are nanometers ( nm ). The units and the value ranges of the parameter values are the same as those of the respective 'constant' parameters. For example, when a loss spectrum is loaded from file it might look like: 1500 1.99E-01 1525 1.92E-01 1550 1.89E-01 1575 1.93E-01 1600 2.05E-01 1500 0.199 1525 0.192 1550 0.189 1575 0.193 1600 0.205 or: 350 NONLINEAR DISPERSIVE FIBER (OBSOLETE) An arbitrary number of points (file lines) are permitted, except 0 (empty file). The column separator can be an arbitrary number (except 0) of either spaces or tabs. The files are opened using the standard Windows "File Open" dialog box. Technical background Origin of the nonlinearity At high optical intensities for intense electromagnetic fields, the dielectric medium behaves as a nonlinear medium. This is also the case for the fiber material. Under the influence of intense electromagnetic fields, the motion of bound electrons becomes anharmonic and, as a result, the induced polarization P from the electric dipoles becomes nonlinear function of the electric field E: P = ε0 [ x (1) .E+x (2) :EE+x (3) :EEE+... ] where χ(j) (j =1,2,3, …) denotes the jth order of susceptibility. The lowest order nonlinearity in optical fibers originates from the third order susceptibility χ(3). Nonlinear effects in optical fibers The following nonlinear effects in optical fibers are caused by the third-order nonlinear susceptibility and are included in the numerical engine of the component: • Self-phase modulation (SPM) • Cross-phase modulation (XPM) • Cross-phase modulation between the orthogonal modes of a birefringent fiber (PXPM) • Four-wave mixing (FWM) • Four-wave mixing between the orthogonal modes of a birefringent fiber (PFWM) • Interchannel Stimulated Raman scattering (SRS) and intrachannel Raman selfshifting (RSS) OptiSystem currently supports several different models specialized for different signal representations and/or combinations of parameters. Model Ia This model has been derived for the separated channels signal representation. It also accounts explicitly for the nonlinear interactions and mixing of the orthogonal polarization modes in an SM fiber. It is a system of 2N coupled modified nonlinear Schrödinger equations (NLSE). This model accounts for: • background loss and linear dispersion up to third order • birefringence and PMD • nonlinearities — SPM, XPM, FWM, SRS, RSS, PXPM, and PFWM 351 NONLINEAR DISPERSIVE FIBER (OBSOLETE) For Sampled signals, the following effects are accounted for: XPM, XPM of orthogonally polarized modes, Raman, FWM, and SSFS. Whereas, for Parameterized signals and ASE noise bins, we account for Raman and FWM. There are 3 types of polarization evolution that could be taken into account: Hi-Bi PM fiber, no PMD, fixed DGD In the case of polarization maintaining fiber, we have to specify the birefringence and DGD of the fiber. Non PM fiber, PMD, stochastic DGD In this case the correlation length Lcorr and PMD coefficient have to be specified. The component allows the calculation for PMD of any order. To see the effect of PMD, the following effects must also be selected under the Effects tab: Birefringence and Group velocity mismatch Averaged polarizations In this case, the effect of the Kerr nonlinearity is averaged over the Poincare sphere, and is taken into account with a coefficient value of 8/9. The effect of nonlinear PMD [2] is not taken into account. The intrapulse Raman scattering (or Raman Self Shifting) effect, which leads to soliton self frequency shift, has to be considered for very short optical pulses with duration ~ picosecond or smaller. The model has the following form: 2 3 ∂A ix ∂A ∂ A ix 1 ∂ A ix 1 ---------- ± β 1ix ---------ix- + --i- β 2i ------------ – --- β 3i ------------- + --- α i A ix = 2 3 ∂z ∂t 2 6 2 ∂t ∂t N f ijkl Mγ x, μ, v, ρ δ ( ω k + ω l – ω j – ω i ) ------- A jμ∗ A kv A lρ exp ( iΔβz ) + f ii j, k, l = 1 ∑ i j, k, l ≠i μ = x v, ρ = x, y 1--- iγA 2 A ∗ exp ( – 2iΔβ xy z ) – iy ix 3 N i ∑ j = 1 ≠1 ωj > ωi j 352 f j n 2 i gR g R ( ω j – ω i ) ---ij- A jx A ix – ig R f ii N ∑ j = 1 ≠1 ωj < ωi j f n 2 g R ( ω i – ω j ) ---ij- A jx A ix f ii NONLINEAR DISPERSIVE FIBER (OBSOLETE) N 2 iγ A ix A ix + 21γ f ij ∑ ---fii- Ajx 2 A ix + j = 1 j 1--- iγ A 2 A + 2--- iγ iy ix 3 3 ≠1 N f ij ∑ ---fii- Ajy 2 A ix + j = 1 j ≠1 2 ∂ A ix iγT R --------------- A ix ∂t (1) where Aix, Aiy are the slowly varying complex electric field amplitudes of the radiation in the respective x/y polarization mode of the i’th WDM channel, β 1 = ( 1 ⁄ v g ) ix and β 1 = ( 1 ⁄ v g ) iy are the inverses of the group velocities of the pol. ix iy modes, evaluated at the respective carrier frequency of the channels. coefficient, related to the dispersion parameter as: β 2i is the GVD 2πcβ 2i D = – ---------------2 λ β 3i is the third-order dispersion coefficient, related to the dispersion slope as: 2 S = ⎛ 2πc ---------⎞ β 3i + ⎛ 4πc ---------⎞ β ⎝ 2⎠ ⎝ 3 ⎠ 2i λ λ αi (2) is the loss coefficient for the respective carrier frequency of the channel n g R is the normalized Raman gain function taken from reference [1], Figure 8.1 on page 300. γ = ωi n2 / c Aeff is the nonlinear coefficient ( ≈ 1-10 W-1km-1 ) 353 NONLINEAR DISPERSIVE FIBER (OBSOLETE) n2 is the nonlinear refractive index equal to 3 χxxxx / 8 neff ( ≈ 3.10-16 cm2/ W ) γ xμνρ = ωi (3 χxμνρ /8 neff )/ (c Aeff ) is the nonlinear coefficient of the four-wave interactions and is proportional to the relevant component of the χ tensor. Aeff is the effective area: ∞ ∞ ∫ ∫ Aeff = 2 ( F ( x ,y ) ) dx dy –∞ – ∞ ------------------------------------------------------∞ ∞ ∫ ∫ 4 F ( x ,y ) dx dy –∞ –∞ (3) where F(x,y) is the modal field distribution of the fiber mode. The overlap integrals fij are defined by: ∞ ∞ ∫ ∫ fii = 2 2 Fi ( x ,y ) F j ( x ,y ) dx dy –∞ – ∞ --------------------------------------------------------------------------------------------------∞ ∞ ∞ ∞ 2 2 F i ( x ,y ) dx dy F j ( x ,y ) dx dy ∫ ∫ –∞ – ∞ ∫ ∫ – ∞ –∞ (4) M is the multiplicity factor. Its value is 2 if all three waves are different — otherwise, its value is 1. The overlap integral fijkl is: fijkl= 354 ⟨ F i∗ F j∗ F k F l⟩ -----------------------------------------------------------------------------2 2 2 2 1⁄2 [ ⟨ Fi ⟩ ⟨ Fj ⟩ ⟨ Fk ⟩ ⟨ Fl ⟩ ] NONLINEAR DISPERSIVE FIBER (OBSOLETE) (5) where the angle brackets denote integration over the transverse coordinates x and y. Also Δβ = ( ω k n k + ω l n l – ω j n j – ω i n i ) ⁄ c (6) where Δβ xy = β y – β x (7) are the propagation constant mismatches of the processes of FWM and (PFWM) and TR ~ 5 fsec is the slope of the Raman gain curve. Model Ib Similar to Model Ia, but disregards the polarization evolution of the signal and uses the average power of the two polarization modes. It consists of a system of only N coupled modified nonlinear Schrödinger equations (NLSE) with correspondingly adjusted nonlinear coefficients. Model I Derived for the case of the total field signal representation. All sampled signals are in a single frequency band. This is the basic method used for modeling WDM systems. It also accounts explicitly for the mixing of the orthogonal polarization modes in an SM fiber. It is a system of two coupled modified nonlinear Schrödinger equations (NLSE). This model accounts for: • background loss and linear dispersion up to third order • birefringence and PMD • nonlinearities - SPM, XPM, FWM, SRS, RSS, PXPM It works with all types of signals: Sampled, Parameterized and ASE noise bins. For parameterized and ASE noise bins, only linear losses are taken into account. 'Total field approach' automatically accounts the XPM and FWM effects. There is no possibility to switch off these effects. 'Total field approach for both polarizations' will additionally account for PXPM of orthogonally polarized signals' and PFWM of orthogonally polarized signals'. The model for the case of one polarization has the following form: 2 3 2 ∂A A- – 1--- β ∂-------A- + 1--- αA = iγ A 2 A – iγT ∂----------A -A ------ ± β 1 ∂A ------ + --i- β 2 ∂-------3 R ∂z ∂t 2 ∂t 2 6 ∂t 3 2 x ∂t (8) 355 NONLINEAR DISPERSIVE FIBER (OBSOLETE) All the parameters in the above equation have been explained, along with the Model Ia. Numerical Methods The three models (Model la, Model lb, and Model l) are solved by a scalar or vectorial version of the split-step Fourier transform method: ∂A ------ = [ D + N ]A ∂z (9) with symmetrized step size [1]. In addition, the step size can be controlled along the propagation. Step size selection rules The user can choose one of the following three ways to calculate the step size: • Fixed • Initial Nonlinear Length / Number of Steps • Current Nonlinear Length / Number of Steps Fixed In this case the step size is simply Δz = L and N is the user defined number of steps. ⁄ N , where L is the length of the fiber Initial Nonlinear Length / Number of Steps One of the well known strategies for guaranteeing accurate split-step calculations is to limit the value of the accumulated nonlinear phase-shift per step. This is equivalent to set Δz = L NL ⁄ N LNL where L NL = 1 ⁄ γP ( 0 ) is the nonlinear length at the input of the fiber (a measure of the distance needed for considerable nonlinear distortions to occur), and N LNL is the user specified number of steps per L NL . Another limitation imposed is that the maximum temporal displacement of the channels due to group-velocity mismatch per step is less than 1% of the bit period. 356 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Current Nonlinear Length / Number of Steps In this case, the nonlinear length is periodically recalculated along the fiber: L NL ( z ) = 1 ⁄ γP ( z ) . In this way, the possible changes in account. L NL ( z ) due to loss or gain are taken into The term indicates the channel used in the calculations above. When the separate channels signal representation is used, it is either the channel with the highest power or the central channel. If we use only one continuous spectral band, as in the total field signal representation, there can be only one main channel. References [1] Agrawal, G.P., “Nonlinear Fiber Optics, 3rd Edition”, Academic Press, 2001. [2] Marcuse, D., Menyuk, C.R., and Wai, P.K.H., "Application of the Manakov - PMD Equation to Studies of Signal Propagation in Optical Fibers with Randomly Varying Birefringence", Journ. Light. Technol.,15, 1735-1746 (1997). [3] Tchofo Dinda, P., Milot, G., and Wabnitz, S. "Polarization Switching and Suppression of Stimulated Raman Scattering in Birefringent Optical Fibers", JOSA B, 15, 1433-1441 (1998). 357 NONLINEAR DISPERSIVE FIBER (OBSOLETE) Notes: 358 LINEAR MULTIMODE FIBER Linear Multimode Fiber This component is a multimode fiber. The component has two modes of operation. The fist one assumes the fiber has sufficient mode mixing due to imperfections or splices; in this case the modal transfer function approaches a Gaussian function. The second one allows the user to load measured modal delays and power-coupling coefficients. The component also includes first- and second-order chromatic dispersion. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Frequency 850 nm, Hz, THz [100, 2000] 1 km,m [0,+INF[ 2.61 dB/km [0,+INF[ False - True, False 1324 MHz.km [0,+INF[ 1 - [0,+INF[ Reference center frequency Length Fiber length Attenuation Fiber attenuation Measured modal delays Defines whether to use measured modal delays (Cambridge Model) or not Modal bandwidth Fiber modal bandwidth Cutback factor Cutback factor 359 LINEAR MULTIMODE FIBER Name and description Default value Default unit Value range Filename CamMMFi.txt - - 300 m, km ]0,+INF[ False - True, False 0 s/km [0,+INF[ 0 s/km [0,+INF[ The name of the file that containing the measured power coupling coefficients and modal delays Reference length The fiber length used for the measurement Frequency response Defines whether to use the calculated frequency response from the measurement or not Propagation delay Propagation delay Delay skew Delay skew Chromatic dispersion Name and description Default value Default unit Value range Include chromatic dispersion False nmHz, THz True, False True — True, False 1354 nm [100, 2000] 0.097 ps / (nm2.km) ]-INF,+INF[ –100 ps / (nm.km) ]-INF,+INF[ 0.5 ps / (nm2.km) ]-INF,+INF[ 0.4 nm [0, 2000] Defines whether the model includes chromatic dispersion effects Use Sellmeier approximations Defines whether the user enters data sheet parameters for zero dispersion wavelength or at the reference wavelength Zero dispersion wavelength Wavelength at zero dispersion Zero dispersion slope Dispersion slope at zero dispersion Dispersion Dispersion at reference frequency Dispersion slope Dispersion slope at reference frequency Spectral width Source spectral width 360 LINEAR MULTIMODE FIBER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ True — — True, False Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Discrete delay If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The optical fiber has three dominant dispersion mechanisms, modal, and first-order chromatic and second-order chromatic. We can assume that modal dispersion and chromatic dispersion mechanisms act independently and can be treated separately[1][2]. Propagation delay and Delay skew parameters are applied to the signal output after the dispersion effects. Modal dispersion Personick has shown that if a multimode fiber has sufficient mode mixing due to imperfections or splices, in this case the modal transfer function approaches a Gaussian function [3][4][5] 2 HM ( ω ) = e 2 ω σ – -----------2 (1) 361 LINEAR MULTIMODE FIBER where ω is the angular baseband frequency and σ is the RMS impulse response width. In this model, the modal dispersion is characterized by the 6 dB half of the optical power frequency: 2 ⋅ 1n ( 2 -) = B ⎛ --1-⎞ γ B 6dB = ------------------------M⎝ ⎠ 2⋅π⋅σ L (2) where B M is defined by the parameter Modal bandwidth and L is the fiber parameter Length. γ is the cutback factor, that takes into account the mode coupling, mixing and concatenation effects. Rewriting Equation 1 and Equation 2 in terms of frequency and bandwidth: HM ( f ) = e ⎛ ⎞ 2 ⎜ 1n ( 2 ) ⋅ f - ⎟ ⎜ – ------------------------------⎟ ⎜ ⎛ B ⋅ ⎛ --1-⎞ γ ⎞ 2 ⎟ ⎝ ⎝ M ⎝ L⎠ ⎠ ⎠ (3) If the Measured modal delays is enable, the modal dispersion is calculated from measured modal delays and power coupling coefficients from parameter Filename. The file format for the modal delay and power coupling coefficients file is the following: Each file contains three columns. The first column contains the order of each mode group supported by the fiber. The second column contains the average modal delay of each mode group, in ns. The third column contains the power-coupling coefficients, which indicate the relative excitation of each mode group. The modal delay is relative to the parameter Reference length. The output signal is calculated from the impulse response of the fiber in time domain. If the parameter Frequency response is enabled, the output signal will be calculated in the frequency domain, in this case, the transfer function of the fiber is calculated according to HM ( f ) = ∑ ( Pm e – j2πfτ m ) (4) m Where P m is the power coupling coefficient and the τ m is the modal delay for mode m. The principle of this model is described in detail in [8]. 362 LINEAR MULTIMODE FIBER Chromatic dispersion Since most of the injection-lasers used in optical fiber communications have a Gaussian line shape [1][2][6][7], we can use the solution for the chromatic transfer function for a perfect Gaussian linewidth case: 2 1 H D ( ω ) = -------------------------------------e 1⁄2 ( 1 + iω ⁄ ω 2 ) ( ω ⁄ ω1 ) – --------------------------------2 ( 1 + iω ⁄ ω2 ) (5) where ω 1 and ω 2 are abbreviations for 2 ω 1 = [ σ λ ( S + 2 D ⁄ λ r )L ] ω1 = –( σλ D L ) –1 (6) –1 where the parameter σ λ is defined by Spectral width, S is the parameter Dispersion slope, D is the Dispersion, λ r is the reference center wavelength calculated from the parameter Frequency, and L is the fiber length. The parameter Use Sellmeier approximations defines whether you will enter D and S directly, or if they will be calculated from the Sellmeier approximations [2]: 4 S ⎛ λ ⎞ D = ----0- ⎜ λ r – ----0-⎟ 3 4⎝ λr ⎠ S ⎛ S = ----0- ⎜ 1 + 4⎝ (7) 4 λ 0⎞ 3 -----⎟ 4 λr ⎠ 363 LINEAR MULTIMODE FIBER References: [1] C. Yabre, "Comprehensive Theory of Dispersion in Graded-Index Optical Fibers", Journal of Lightwave Technology, Vol. 18, No. 2, pp. 166-176, February 2000. [2] G.D. Brown, "Bandwidth and Rise Time Calculations for Digital multimode Fiber-Optical Data Links", Journal of Lightwave Technology, Vol. 10, No. 5, pp. 672-678, May 1992. [3] S.D.Personick "Baseband Linearity and Equalization in Fiber Optic Digital Communication Systems", The Bell System Technical Journal, pp. 1174-1194, September 1973. [4] D.G.Duff, "Computer-Aided Design Of Digital Lightwave Systems", IEEE Journal on Selected Areas in Communications, Vol. SAC-2, No. 1, pp. 171-185, January 1984. [5] D.O.Harris, J.R. Jones "Baud Rate Response: Characterizing Modal Dispersion for Digital Fiber Optic Systems", Journal of Lightwave Technology, Vol. 6, No. 5, pp. 668-677, May 1988. [6] J.L.Gimlett, N,K,Cheung "Dispersion Penalty Analysis for LED/Single-Mode Fiber Transmission Systems", Journal of Lightwave Technology, Vol. LT-4, No. 9, pp. 1381-1391, September 1986. [7] T. Pfeiffer, M. Witte, B. Deppisch "High-Speed Transmission of Broad-Band Thermal Light Pulses Over Dispersion Fibers", IEEE Photonic Technology Letters, Vol. 11, No. 3, pp. 385387, March 1999. [8] M. Webster et al., “A statistical analysis of conditioned launch for Gigabit Ethernet links using multimode fiber”, Journal of Lightwave Technology, Vol. 17, No. 9, pp. 1532-1541, September 1999. 364 PARABOLIC-INDEX MULTIMODE FIBER Parabolic-Index Multimode Fiber This component is a multimode fiber with a parabolic refractive index. It is a spatially dependent component that models the transverse field profiles and propagation constants for each mode supported by the fiber. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 1 km m, km [0, 100000] 2.61 dB/km Name and description Default value Default unit Core radius 25 um [1, 100] 10 um [1, 10000] Defines the fiber length Attenuation [0, 1e+010] Defines the fiber attenuation Fiber Profile Units Value range Defines the fiber core radius Clad radius Defines the fiber clad radius Refractive index peak 1.4142 [1, 2] The peak value of the refractive index for the parabolic profile 365 PARABOLIC-INDEX MULTIMODE FIBER Name and description Default value Default unit Refractive index step 1 % Units Value range [0.01, 10] The delta parameter of the refractive index for the parabolic profile Number of radial steps 1000 [10, 100000] The number of steps for the parabolic profile Chromatic Dispersion Name and description Default value Include chromatic dispersion NO Default unit Units Value range [YES, NO] Defines whether chromatic dispersion effects are included or not Reference wavelength 820 nm [100, 2000] Dispersion and dispersion slope are provided at this reference wavelength Use Sellmeier approximations YES [YES, NO] Defines whether Sellmeier approximations are used or not Zero dispersion wavelength 1354 nm [100, 2000] 0.097 ps/(nm^2.km) [-1e+100, 1e+100] –100 ps/(nm.km) [-1e+100, 1e+100] 0.5 ps/(nm^2.km) [-1e+100, 1e+100] Name and description Default value Default unit User defined wavelength NO The wavelength where the dispersion is zero. The zero dispersion slope is also provided for this wavelength. Zero dispersion slope The dispersion slope at the zero dispersion wavelength Dispersion Dispersion at the reference wavelength Dispersion slope Dispersion slope at the reference wavelength Numerical Defines whether to calculate the mode solver at a user defined wavelength or not 366 Units Value range [YES, NO] PARABOLIC-INDEX MULTIMODE FIBER Name and description Default value Default unit Solver wavelength 820 nm Units Value range [100, 2000] Mode solver is calculated at this wavelength Modal attenuation NO [YES, NO] Defines whether to load a file with modal attenuations or no Attenuation filename Attenuation.dat The filename with the refractive index profile Relative delay YES [YES, NO] NO [YES, NO] Defines whether the differential mode delay is absolute or relative Const. mode power dist. Defines whether to generate a constant mode power distribution (MDP) or not LP(m,n) max. 20, 10 The maximum LP mode index value when the mode solver is searching for modes Min. signal power -100 dBm [-1e+100, 0] The minimum signal power for a given mode. Modes will not be attached to signals with power lower than this value. Generate overfilled launch NO [YES, NO] YES [YES, NO] Defines whether to generate an overfilled fiber launch or not Generate report Defines whether to generate a report with the attributes of the fiber Report The summary of fiber attributes, including number of modes, coupling coefficients and delays 367 PARABOLIC-INDEX MULTIMODE FIBER Graphs Name and description Default value Default unit Units Value range Calculate graphs NO [YES, NO] Power Phase [Power Phase, Real Imag] Defines whether to calculate graphs or not Format Defines whether to calculate the graphs using rectangular or polar format Wavelength 820 nm [100, 2000] The reference wavelength for the graphs LP(m,n) 0, 1 The LP mode index for the individual radial and mode profile graphs Radial graphs YES [YES, NO] YES [YES, NO] NO [YES, NO] NO [YES, NO] Defines whether to calculate the radial graphs Mode number graphs Defines whether to calculate the mode number graphs Spatial profile graphs Defines whether to calculate the spatial profile graphs Spatial overfilled graphs Defines whether to calculate the spatial overfilled graphs Simulation Name and description Default value Enabled YES Default unit Units [YES, NO] Determines whether or not the component is enabled Graphs Name and description X Title Y Title Refractive index profile Radius (m) Refractive index LP[m,n] index array - m Mode number m 368 Value range PARABOLIC-INDEX MULTIMODE FIBER Name and description X Title Y Title LP[m,n] index array - n Mode number n Group delay Mode number Group delay (ps/km) Effective index Mode number Effective index Radial profile - individual a Radius (m) Intensity Radial profile - individual b Radius (m) Phase (rad) Spatial profile - individual a X (m) Y (m) Spatial profile - individual b X (m) Y (m) Spatial profile - overfilled a X (m) Y (m) Spatial profile - overfilled b X (m) Y (m) Power coupling and modal delay Modal delay (s) Power coupling Technical Background This component is a multimode fiber with parabolic refractive index (Figure 1). The parabolic profile is described analytically as [1]: where n1 is the parameter Refractive peak index at the fiber center, n2 is the refractive index in the cladding, Δ is the parameter Refractive index step, a is the parameter Core radius and (b-a) is the parameter Clad radius. The radial distance from the fiber center r is discretized using the parameter Number of radial steps. 369 PARABOLIC-INDEX MULTIMODE FIBER Figure 1 Parabolic refractive index profile The main result of the fiber calculation is the spatial profile, coupling coefficients and the time delay for each mode.The signal center frequency for the mode solver depends on the center frequency of the input signal. The user can force the mode solver to work at a user defined wavelength by enabling parameter User defined wavelength. Additionally, the user can provide a file with the modal attenuation. The modal attenuation file format is a list with the m and n mode index and the attenuation in dB/km for polarizations X and Y: Figure 2 Modal attenuation file For illustration purposes, in the file above, 4 modes will be attenuated: LP 0, 1 , LP 0, 2 , LP 1, 1 and LP –1, 1 . The first mode will be attenuated by 0 dB/km for both polarizations. The next mode will be attenuated by 500000 dB/Km. The remaining two modes will be attenuated by 2000 dB/km. The final solution for the output field of the combined temporal and spatial properties of the fiber for N number of modes is shown below: where Ein is the signal input field, ci is the coupling coefficient between the fiber modes and the spatial profile if the input field and Ei is the fiber mode for each index i. 370 PARABOLIC-INDEX MULTIMODE FIBER If the power of (ci.Ein) is below the parameter Min. signal power, the signal i is discarded. The component has an analytical mode solver that will calculate the LP(m,n) modes. The parameter LP(m,n) max. defines the maximum order for the radial and azimuthal indexes m and n when searching for fiber modes. The analytical solution for the field in the core, for each m and n index is [1]: where Ea,0 is a scaling factor for the boundary conditions in the core/clad fiber interface. L is the Laguerre polynomial function, and k0 and ρ are given by: where λ 0 is the center wavelength. The solution in the clad is given by: where Eb,0 is a scaling factor for the boundary conditions in the clad/core fiber interface, K is the modified Bessel function. The propagation constant β m, n is calculated accordingly to: There are two main results of this calculation. They are the time delay associated with each mode and the coupling coefficient between the input spatial fields and each of the spatial fiber modes. The propagation constant β is used to calculate the time delay per mode: 371 PARABOLIC-INDEX MULTIMODE FIBER where L is the fiber length. The coupling coefficient is calculated according to: where Ei is the spatial profile for each m,n mode, including the sin and cosine factors, and Ein is the spatial input field. The user can also generate a constant mode power distribution (MPD). In this case the coefficients will be constant. Enabling the parameter Generate overfilled launch can generate an overfilled launch mode. After the calculation, the parameter Report will have a list of the modes, coupling coefficients and delays for each mode and polarization. Another advanced feature of this model is the graph calculations. By enabling the parameter Calculate graphs, the user can see the results from the analytical mode solver. The results can include the mode index number for the calculated modes, the effective index, delays, power coupling, refractive index profiles, and spatial and radial profiles for the individual and overfilled mode. The fiber model also includes the chromatic dispersion effects. If chromatic dispersion is enabled, the user can specify the value of the dispersion and dispersion slope, as well as Sellmeier. The parameter Use Sellmeier approximations defines whether to calculate dispersion and slope from the Sellmeier approximations[2]: References [1] A. Ghatak, K. Thyagarajan, “Introduction to Fiber Optics”, Cambridge University Press, New York, NY, 1998. [2] G.D. Brown, "Bandwidth and Rise Time Calculations for Digital multimode Fiber-Optic Data Links", Journal of Lightwave Technology, VOL. 10, NO 5, May 1992, pp. 672-678. 372 MEASURED-INDEX MULTIMODE FIBER Measured-Index Multimode Fiber This component is a general-purpose multimode fiber with user-defined refractive index profile. It is a spatially dependent component that models the transverse field profiles and propagation constants for each mode supported by the fiber. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 1 km m, km [0, 100000] 2.61 dB/km Name and description Default value Default unit OptiFiber file format NO Defines the fiber length Attenuation [0, 1e+101] Defines the fiber attenuation Fiber Profile Units Value range [YES, NO] Defines whether to load a file generated by OptiFiber or not Filename Index.txt The filename with the refractive index profile 373 MEASURED-INDEX MULTIMODE FIBER Chromatic Dispersion Name and description Default value Include chromatic dispersion NO Default unit Units Value range [YES, NO] Defines whether chromatic dispersion effects are included or not Reference wavelength 820 nm [100, 2000] Dispersion and dispersion slope are provided at this reference wavelength Use Sellmeier approximations YES [YES, NO] Defines whether Sellmeier approximations are used or not Zero dispersion wavelength 1354 nm [100, 2000] 0.097 ps/(nm^2.km) [-1e+100, 1e+100] –100 ps/(nm.km) [-1e+100, 1e+100] 0.5 ps/(nm^2.km) [-1e+100, 1e+100] Name and description Default value Default unit User defined wavelength NO The wavelength where the dispersion is zero. The zero dispersion slope is also provided at this wavelength. Zero dispersion slope The dispersion slope at the zero dispersion wavelength Dispersion Dispersion at the reference wavelength Dispersion slope Dispersion slope at the reference wavelength Numerical Units Value range [YES, NO] Defines whether to calculate the mode solver at a user defined wavelength or not Solver wavelength 820 nm [100, 2000] Mode solver is calculated at this wavelength Modal attenuation Defines whether to load a file with modal attenuations or no 374 NO [YES, NO] MEASURED-INDEX MULTIMODE FIBER Name and description Default value Attenuation filename Attenuation.dat Default unit Units Value range The filename with the refractive index profile Relative delay YES [YES, NO] NO [YES, NO] Effective index diff. [Effective index diff., WentzelKramers-Brillouin, Variation principle] 20, 10 [0, 1000] Defines whether the differential mode delay is absolute or relative Const. mode power dist. Defines whether to generate a constant mode power distribution (MDP) or not Modal delay Defines whether to calculate the differential mode delay using WentzelKramers-Brillouin (WKB) or not LP(m,n) max. The maximum LP mode index value when the mode solver is searching for modes Min. signal power -100 dBm [-1e+100, 0] The minimum signal power for a given mode. Modes will not be attached to signals with power lower than this value. Mode solver LP LP, OptiFiber Solver tolerance 1e-014 [1e-100, 0.1] Solver step size 1.5e-005 [1e-100, 1] Solver sample rate 25 Generate overfilled launch NO [YES, NO] YES [YES, NO] 1/um [10, 1000] Defines whether to generate an overfilled fiber launch or not Generate report Defines whether to generate a report with the attributes of the fiber Report The summary of fiber attributes, including number of modes, coupling coefficients and delays 375 MEASURED-INDEX MULTIMODE FIBER Graphs Name and description Default value Default unit Units Value range Calculate graphs NO [YES, NO] Power Phase [Power Phase, Real Imag] Defines whether to calculate graphs or not Format Defines whether to calculate the graphs using rectangular or polar format Wavelength 820 nm [100, 2000] The reference wavelength for the graphs LP(m,n) 0, 1 [0, 1000] YES [YES, NO] YES [YES, NO] NO [YES, NO] NO [YES, NO] The LP mode index for the individual radial and mode profile graphs Radial graphs Defines whether to calculate the radial graphs Mode number graphs Defines whether to calculate the mode number graphs Spatial profile graphs Defines whether to calculate the spatial profile graphs Spatial overfilled graphs Defines whether to calculate the spatial overfilled graphs Simulation Name and description Default value Enabled YES Default unit Units [YES, NO] Determines whether or not the component is enabled Graphs Name and description X Title Y Title Refractive index profile Radius (m) Refractive index LP[m,n] index array - m Mode number m 376 Value range MEASURED-INDEX MULTIMODE FIBER Name and description X Title Y Title LP[m,n] index array - n Mode number n Group delay Mode number Group delay (ps/km) Effective index Mode number Effective index Radial profile - individual a Radius (m) Intensity Radial profile - individual b Radius (m) Phase (rad) Spatial profile - individual a X (m) Y (m) Spatial profile - individual b X (m) Y (m) Spatial profile - overfilled a X (m) Y (m) Spatial profile - overfilled b X (m) Y (m) Power coupling and modal delay Modal delay (s) Power coupling Technical Background This component is a general-purpose multimode fiber with a user-defined index profile. The user should provide the fiber refractive index as an input file. The main result of the fiber calculation is the spatial profile, coupling coefficients and the time delay for each mode. The final solution for the output field of the combined temporal and spatial properties of the fiber for N number of modes is: where Ein is the signal input field, ci is the coupling coefficient between the fiber modes and the spatial profile if the input field and Ei is the fiber mode for each index i. If the power of (ci.Ein) is below the parameter Min. signal power, the signal i is discarded. The component has a numerical mode solver that will calculate the LP(m,n) modes and the propagation constants. The parameter LP(m,n) max. defines the maximum order for the radial and azimuthal indexes m and n when searching for fiber modes. The signal center frequency for the mode solver depends on the center frequency of the input signal. The user can force the mode solver to work at a user defined wavelength by enabling parameter User defined wavelength. The parameter OptiFiber file format defined whether the refractive index file was generated by Optiwave OptiFiber[2] (or Fiber_CAD) software tool. The refractive index file format is a list with the radial position from the center of the fiber to the clad, and the real value of the refractive index. The radial position should be provided in microns: 377 MEASURED-INDEX MULTIMODE FIBER Figure 1 File with fiber profile, radius (first column) should be given in microns IMPORTANT: the first radial position should be different from zero. If the OptiFiber format is enabled, the file should also include the header and the number of radial points (Figure 2). 378 MEASURED-INDEX MULTIMODE FIBER Figure 2 File with fiber profile using OptiFiber format, radius (first column) should be given in microns There are two main results of this calculation, the time delay associated with each mode, and the coupling coefficient between the input spatial fields and each of the spatial fiber modes. Additionally, the user can provide a file with the modal attenuation. The modal attenuation file format is a list with the m and n mode index and the attenuation in dB/km for polarizations X and Y: Figure 3 Modal attenuation file For illustration purposes, in the file above, 4 modes will be attenuated: LP 0, 1 , LP 0, 2 , LP 1, 1 and LP –1, 1 . The first mode will be attenuated by 0 dB/km for both polarizations. The next mode will be attenuated by 500000 dB/Km. The remaining two modes will be attenuated by 2000 dB/km. 379 MEASURED-INDEX MULTIMODE FIBER The propagation constant β is used to calculate the time delay per mode. There are two options to calculate the delay. The first option uses the Wentzel-Kramers-Brillouin method: where n1 is the peak value of the refractive index, L is the fiber length, c is the speed of light and λ 0 is the center wavelength. The second method is to apply the derivative of the effective index directly to calculate the delay: The third method is to apply the variation principle to calculate the delay, avoiding the numerical errors of the derivative: The coupling coefficient is calculated according to: where Ei is the spatial profile for each m,n mode, including the sin and cosine factors, and Ein is the spatial input field. 380 MEASURED-INDEX MULTIMODE FIBER The user can also generate a constant mode power distribution (MPD). In this case the coefficients will be constant. Enabling the parameter Generate overfilled launch can generate an overfilled launch mode. After the calculation, the parameter Report will have a list of the modes, coupling coefficients, and delays for each mode and polarization. Another advanced feature of this model is the graph calculations. By enabling the parameter Calculate graphs, the user can see the results from the analytical mode solver. The results can include the mode index number for the calculated modes, the effective index, delays, power coupling, the refractive index profile, and spatial and radial profiles for the individual and overfilled mode. The fiber model also includes the chromatic dispersion effects. If chromatic dispersion is enabled, the user can specify the value of the dispersion and dispersion slope, as well as Sellmeier approximations. The parameter Use Sellmeier approximations defines whether to calculate dispersion and slope from the Sellmeier approximations[3]: References [1] A. Ghatak, K. Thyagarajan, Introduction to Fiber Optics, Cambridge University Press, New York, NY, 1998. [2] OptiFiber 1.5 documentation, Optiwave Corporation, www.optiwave.com. [3] G.D. Brown, "Bandwidth and Rise Time Calculations for Digital Multimode Fiber-Optic Data Links", Journal of Lightwave Technology, VOL. 10, NO 5, May 1992, pp. 672-678. 381 MEASURED-INDEX MULTIMODE FIBER Notes: 382 Free Space Optics Library This section contains information on the following components • FSO Channel • OWC Channel 383 FREE SPACE OPTICS LIBRARY Notes: 384 FSO CHANNEL FSO Channel This component models a free space optics (FSO) channel. It is a subsystem of two telescopes and the free space channel between them. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Sample signals Parameters Main Name and description Default value Default unit Units Value range Range 1 km m, km [0, 1e+100] 25 dB/km The distance between the transmitter and the receiver telescopes Attenuation [0, 1e+100] The attenuation caused by atmospheric effects Geometrical loss True True, False Define whether calculate the geometrical loss or not Transmitter aperture diameter 5 cm mm, cm, m [0, 1e+100] 20 cm mm, cm, m [0, 1e+100] The aperture diameter of the transmitter telescope Receiver aperture diameter The aperture diameter of the receiver telescope 385 FSO CHANNEL Name and description Default value Default unit Units Value range Beam divergence 2 mrad [0, 1e+100] 0 dB [0, 1e+100] 0 dB [0, 1e+100] 0 dB [0, 1e+100] 0 ps/km [0, 1e+100] Name and description Default value Default unit Enabled True True, False True True, False 1/e for Gaussian beams, FWHA for flat top beams Transmitter loss Fiber-telescope coupling and transmitter efficiency losses Receiver loss Telescope-fiber coupling and receiver efficiency losses Additional losses Losses due to scintillation, mispointing, etc. Propagation delay Signal propagation delay Simulation Units Value range Determines whether or not the component is enabled Discrete delay If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value Technical Background This component allows for simulation of free space optical links [1][2][3]. The component is a subsystem of transmitter telescope, free space and receiver telescope. Parameter Range defines the propagation distance between transmitter and receiver telescope. The attenuation of the laser power in depends on two main parameters: Attenuation and Geometrical loss. The first parameter describes the attenuation of the laser power in the atmosphere. The second parameter, Geometrical loss, occurs due to the spreading of the transmitted beam between the transmitter and the receiver. The link equation is [1]: 386 FSO CHANNEL PRe ceived = PTransmitted d R2 10 −αR / 10 2 (d T + θR) Where: dR : Receiver aperture diameter (m) dT : Transmitter aperture diameter (m) θ: Beam divergence (mrad) R : Range (km) α: Atmospheric attenuation (dB/km) The user can also specify the transmitter and receiver losses due to fiber-telescope interface and coupling efficiencies (parameters Transmitter loss and Receiver loss). Additional losses due to scintillation, mispointing, and others can be specified by the parameter Additional losses. Parameter Propagation delay allows for calculation of the delay between transmitter and receiver. References [1] S. Bloom, E. Korevaar, J. Schuster, H. Willebrand, 'Understanding the performance of freespace optics', Journal of Optical Networking. Vol. 2, No. 6, pp. 178-200, June 2003. [2] D. Killinger, 'Free Space Optics for Laser Communication through the Air', Optics and Photonics News , pp. 36-42, October 2002 [3] I. I. Kim et al, "Wireless optical transmission of fast Ethernet, FDDI, ATM and ESCON protocol data using the TerraLink laser communication system" Optical Engineering, vol. 37, no. 12, pp. 3143-3155, December 1998 387 FSO CHANNEL Notes: 388 OWC CHANNEL OWC Channel This component models an optical wireless communication (OWC) channel. It is a subsystem of two telescopes and the wireless communication channel between them. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Sample signals Parameters Main Name and description Default value Default unit Units Value range Frequency 1550 nm Hz, THz, nm [100, 2000] 200 km m, km [0, 1e+100] The distance between the transmitter and the receiver telescopes Range The distance between the transmitter and the receiver telescopes Geometrical gain True True, False Define whether calculate the geometrical gain or not Transmitter aperture diameter 15 cm mm, cm, m [0, 1e+100] 15 cm mm, cm, m [0, 1e+100] 0 dB The aperture diameter of the transmitter telescope Receiver aperture diameter The aperture diameter of the receiver telescope Transmitter gain [0, 1e+100] Fiber-telescope transmitter gain 389 OWC CHANNEL Name and description Default value Default unit Receiver gain 0 dB Units Value range [0, 1e+100] Telescope-fiber receiver gain Transmitter optics efficiency 1 [0, 1] 1 [0, 1] Fiber-telescope transmitter efficiency Receiver optics efficiency Telescope-fiber receiver efficiency Transmitter pointing error angle 0 urad urad, mrad, rad [0, 1e+100] 0 urad urad, mrad, rad [0, 1e+100] 0 dB/km [0, 1e+100] 0 dB [0, 1e+100] 0 ps/km [0, 1e+100] Name and description Default value Default unit Enabled True True, False True True, False Telescope transmitter pointing error Receiver pointing error angle Receiver telescope pointing error Attenuation The attenuation caused by atmospheric effects Additional losses Losses due to scintillation, mispointing, etc. Propagation delay Signal propagation delay Simulation Units Value range Determines whether or not the component is enabled Discrete delay If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value 390 OWC CHANNEL Technical Background This component allows for simulation of free space optical links [1][2]. The component is a subsystem of transmitter telescope, optical wireless communication channel and receiver telescope. The optical signal received at the receiver is given by: λ -⎞ 2 G G L L PR = P T η T η R ⎛ --------⎝ 4πZ⎠ T R T R (1) P T is the transmitter optical power; η T is the optics efficiency of the transmitter; η R is the optics efficiency of the receiver; λ is the wavelength; Z is where the distance between the transmitter and the receiver, given by the parameter Range; G T is the transmitter telescope gain; G R is the receiver telescope gain; and L T , L R are the transmitter and the receiver pointing loss factor, respectively. The term in parentheses is the free-space loss. Parameter Geometrical gain defines whether the user will enter the transmitter and receiver gain directly or estimate the gain for a diffraction-limited beam. The gain that can be expressed by: πD 2 G T ≈ ⎛ ---------T-⎞ ⎝ λ ⎠ (2) where D T is the transmitter telescope diameter. Similarly, the receiver telescope gain that can be expressed by: πD G R ≈ ⎛⎝ ----------R⎞⎠ λ where 2 (3) D R is the receiver telescope diameter. Most systems use a narrow-beam-divergence angle laser transmitter and narrow field of view receiver; hence small mispointing can cause signal loss. The approximation transmitter pointing loss factor is given by: 2 (4) L T = exp ( – G T θT ) 391 OWC CHANNEL where θ T is transmitter azimuth pointing error angle, and the approximation receiver pointing loss factor by: 2 L R = exp ( – G R θ R ) where (5) θ R is receiver azimuth pointing error angle. Additional losses due to scintillation, mispointing, and others can be specified by the parameter Additional losses. Parameter Propagation delay allows for calculation of the delay between transmitter and receiver. References [1] A. Polishuk, S. Arnon, 'Optimization of a laser satellite communication system with an optical preamplifier', J. Optical Society of America. Vol. 21, No. 7, pp 1307-1315, July 2004.. [2] S. Arnon, 'Performance of a laser satellite network with an optical preamplifier', J. Optical Society of America. Vol. 22, No. 4, pp 708-715, April 2005. 392 RECEIVERS LIBRARY Receivers Library This section contains information on the following receivers. Multimode • Mode Combiner • Mode Selector Regenerators • Clock Recovery • Data Recovery • 3R Regenerator • Electronic Equalizer • MLSE Equalizer • Integrate And Dump Demodulators • Ideal Frequency Demodulator • Ideal Phase Demodulator Optical Receivers • Optical Receiver • Spatial Optical Receiver Photodetectors • Photodetector PIN • Photodetector APD • Spatial PIN Photodetector • Spatial APD Photodetector 393 RECEIVERS LIBRARY Notes: 394 MODE COMBINER Mode Combiner This component combines multiple signals with transverse mode profiles into one single-mode signal. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Simulation Name and description Default value Enabled YES Value range [YES, NO] Determines whether or not the component is enabled Technical Background This component combined the time-dependent waveform of multiple modes into one single-mode signal. It assumes that the spatial fields attached to each waveform are orthogonal. 395 MODE COMBINER Notes: 396 MODE SELECTOR Mode Selector This new component extracts a single mode from a multimode signal. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Simulation Name and description Default value Value range Individual mode number 0 [0,+INF[ YES [YES, NO] Determines whether or not the component is enabled Centered at max power Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center wavelength 820 nm Hz, THz, nm [100, 2000] Name and description Default value Default unit Units Value range Enabled YES User-defined center frequency for the internal filter Simulation [YES, NO] Determines whether or not the component is enabled 397 MODE SELECTOR Technical Background This new component extracts a single mode from a multimode signal. The user can select the mode index and the mode wavelength. 398 CLOCK RECOVERY Clock Recovery Compensates the time delay between the original signal at the reference port and the signal that is received at the input port. Ports Name and description Port type Signal type Reference Input Electrical Input Input Electrical Output Output Electrical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Results Name and description Units Signal delay s Signal delay samples Technical background The time delay is calculated from cross-correlation of the reference signal and the received signal. The signal is then shifted in time. 399 CLOCK RECOVERY Notes: 400 DATA RECOVERY Data Recovery This component recovers the binary data from the electrical signal. It can be used in 3R generators for the data recovery stage. Ports Name and description Port type Signal type Input Input Electrical Bit sequence Output Binary Parameters Main Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s [0,+INF[ Reference bit rate to use for the decision instant calculation User defined delay MBits/s GBits/s False — — True, false 0 s s, ms, ns ]-INF,+INF[ False — — True, false 0.5 Bit — [0,1] Defines whether the user can define the delay compensation or not Delay compensation Delay to apply to the signal input User defined decision Defines whether the component will automatically calculate the decision instant or it will be defined by the user Decision instant Value for the decision instant to use when recovering the bit sequence 401 DATA RECOVERY Name and description Default value Default unit Units Value range User defined threshold False — — True, false 0.5 a.u. — ]-INF,+INF[ Defines whether the component will be automatically calculated or will be userdefined Absolute threshold Value for the threshold to use when recovering the bit sequence Random numbers Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background This component allows the user to recover a bit sequence from an electrical signal. In order to recover the bit sequence, the user should provide the signal bit rate, given by the parameter Reference bit rate. The decision instant and the threshold level can be defined by the user or automatically calculated by this component. If the parameter User defined decision is disabled, the model automatically estimates the decision instant by generating internally an eye diagram and searching for the maximum opening for the eye amplitude. The time instant with the maximum opening is the decision instant, this method is valid for RZ and NRZ modulation types. The user can disable the searching and enter directly the value of the decision instant by disabling User defined decision and entering the instant using the parameter Decision instant. If the parameter User defined threshold is disabled, the threshold is calculated at the decision instant, by searching for the maximum eye opening. The threshold value will be at the center of the maximum eye opening. The user can disable the searching and enter directly the value of the threshold by disabling User defined threshold and entering the threshold using the parameter Absolute threshold. The parameter Delay compensation allows the user to compensate the propagation delays of the input signal by enabling the parameter User defined delay. If the parameter User defined delay is disable, the delay will be estimated by comparing the input signal with a signal generated by the internal clock. 402 3R REGENERATOR 3R Regenerator This component regenerates an electrical signal. Ports Name and description Port type Signal type Input Input Electrical Bit sequence Output Binary Reference signal Output Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s [0,+INF[ Reference bit rate to use for the decision instant calculation User defined delay MBits/s GBits/s False — — True, false 0 s s, ms, ns ]-INF,+INF[ False — — True, false 0.5 Bit — [0,1] Defines whether the user can define the delay compensation or not Delay compensation Delay to apply to the signal input User defined decision Defines whether the component will automatically calculate the decision instant or it will be defined by the user Decision instant Value for the decision instant to use when recovering the bit sequence 403 3R REGENERATOR Name and description Default value Default unit Units Value range User defined threshold False — — True, false 0.5 a.u. — ]-INF,+INF[ Defines whether the component will be automatically calculated or will be userdefined Absolute threshold Value for the threshold to use when recovering the bit sequence Technical background This component regenerates an electrical signal. It generates the original bit sequence, and a modulated electrical signal to be used for BER analysis. It is a subsystem based on the Data Recovery component and a NRZ Pulse Generator. This first output port is the bit sequence, the second one is a modulated NRZ signal and the last output is a copy of the input signal. These three signals can be connected directly to the BER Analyzer, avoiding additional connections between transmitter and the receiver stage. The following system shows a conventional connection between the BER Analyzer in the receiver stage with the transmitter stage, 2 additional connections are required between the transmitter and the BER Analyzer. 404 3R REGENERATOR By using the 3R Regenerator, there is no need for connections between the transmitter and the BER Analyzer. This is especially important for WDM systems, where you have with multiple transmitters, receivers and BER Analyzers. For more information, see “Spatial CW Laser”. 405 3R REGENERATOR Notes: 406 ELECTRONIC EQUALIZER Electronic Equalizer This component is an electronic equalizer. It can work as a fractionally or spaced feedforward equalizer (FFE), decision-feedback equalizer (DFE) or the combination of both. A least mean square (LMS) algorithm is used to update the filter tap coefficients Ports Name and description Port type Signal type Supported Modes Input Input Electrical Sampled signals Training Input Electrical Sampled signals Output Output Electrical Sampled signals Parameters Main Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s [0,+INF[ Reference bit rate to use for the decision instant calculation and tap delays Update taps coefficients MBits/s GBits/s False True, False True True, False False True, False Define whether update the tap coefficients using the LMS algorithm Linear feedback Define whether use the decision or linear output as the DFE input Decision output Define whether use the decision or linear output as the equalizer output 407 ELECTRONIC EQUALIZER LMS Name and description Default value Default unit Units Value range Limit training sequence length False [True, False 100 [0, 1e+100] 0.03 [0, 1e+100] 1 [0, 1e+100] Define whether calculate the sequence length from the training input signal of limit to a user defined value Training sequence length User defined sequence length Step size Step size for the LMS algorithm Leakage factor Leakage factor for the LMS algorithm Report The summary of filter tap coefficients before and after training and calculation Decision stage Name and description Default value Default unit Units Value range High level input 1 (a.u) [-1e+100,1e+100] 0 (a.u) [-1e+100,1e+100] 0.5 (a.u) [-1e+100,1e+100] 0.5 Bit [0,1] Name and description Default value Default unit Forward taps space 1 (HLI) Value for the high level input in the decision stage Low level input (LVI) Value for the low level input in the decision stage Absolute threshold Value for the threshold to use when recovering the bit sequence. Typically (HLI + LVI) / 2 Decision instant Value for the decision instant to use when recovering the bit sequence Forward taps The inverse of the tap delay ratio. It is a spaced equalizer if value is equal to one or a fractionally spaced otherwise 408 Units Value range [1, 100] ELECTRONIC EQUALIZER Name and description Default value Default unit Units Value range Forward taps coefficients 3 [0, 10000] 1 [-1e+100,1e+100] 0 [-1e+100,1e+100] Number of forward taps coefficients Forward[0].real Real part of the first tap coefficient Forward[0].imag Imaginary part of the first tap coefficient ... [-1e+100,1e+100] Feedback taps Name and description Default value Default unit Units Value range Feedback taps coefficients 3 [0, 10000] 1 [-1e+100,1e+100] 0 [-1e+100,1e+100] Number of feedback taps coefficients Feedback[0].real Real part of the first tap coefficient Feedback[0].imag Imaginary part of the first tap coefficient ... [-1e+100,1e+100] Graphs Name and description Default value Calculate graphs YES Default unit Units Value range [YES, NO] Determines whether calculate the error level graphs for the output and training signal Simulation Name and description Default value Enable YES Default unit Units Value range [YES, NO] Determines whether or not the component is enabled 409 ELECTRONIC EQUALIZER Graphs Name and description X Title Y Title Training error Bits Error level (a.u.) Calculation error Bits Error level (a.u.) Technical background An electronic equalizer attempts to mitigate intersymbol interference (ISI) caused by time-dispersive channels, such as chromatic dispersion and polarization mode dispersion (PMD) in single mode fibers [1], or differential mode delay (DMD) in multimode fibers [2]. This component can work as a fractionally or spaced feed-forward equalizer (FFE), decision-feedback equalizer (DFE) or the combination of both. A least mean square (LMS) algorithm is used to update the filter tap coefficients. The signal input x(t) is filtered by a forward filter, or a linear equalizer. Parameter Forward taps coefficients define the number of forward tap coefficients for the filter. Forward taps space defines the tap spaces, or the K parameter in the schematic bellow. If K is greater than one the filter is fractionally spaced. Figure 1 410 Equalizer schematic ELECTRONIC EQUALIZER At the output of the forward filter, the output signal y'(t) goes to a decision stage where the signal is detected based on the parameters Threshold and Decision instant. The detected signal will have values of high and low level depending on parameters High level and Low level. Parameter Decision output defines if the output signal y(t) is y'(t) or the detected signal yd(t). The user can also select whether the input to the feedback filter stage is the detected signal yd(t) or the linear signal y'(t) (parameter Linear feedback). The training input signal is used to calculate the filter coefficients, based on the LMS algorithm, where the error is calculated according to: e k = y' k – d k (1) The filter taps (w) coefficients are updated according to w k + 1 = w k l + Δu k∗ e k (2) Where l is the parameter Leakage factor and Δ is the parameter Step size. The user can disable the filter updates by setting parameter Update taps coefficients to false. By default, the equalizer will estimate the filter coefficients using the training sequence. The user can limit the training sequence to a value defined by the parameter Training sequence length. If the user wants to disable the training simply set this parameter to zero or connect the training input to a electrical null component. The values for the error level ek are available in two graphs. The first graphs plots the error values versus for the training sequence, the second graph plots the error values for the detected signal. The user can provide the tap coefficients as an initial value for the equalizer, or the component can also be used as a linear FIR filter by disabling Update tap coefficients and limiting the training sequence length to zero. Alternatively, setting the Step size to zero also disables the updating of the tap coefficients and the initial values will not change during the calculation. Parameter Report presents the values of the filter coefficients before and after the training, and at the end of the calculation. References: [1] J. Wang and J. M. Kahn, 'Performance of electrical equalizers in optically amplified OOK and DPSK systems', IEEE Photon. Technol. Lett. 16, 5, pp. 1397-1399, May 2004 [2] H. Wu et al, "Integrated transversal equalizers in high-speed fiber-optic systems," IEEE J. Solid-State Circuits, vol. 38, no. 12, pp. 2131-2137, Dec. 2002. 411 ELECTRONIC EQUALIZER Notes: 412 MLSE EQUALIZER MLSE Equalizer This component is a MLSE (maximum likelihood sequence estimate) electronic equalizer. The component uses the Viterbi algorithm to equalize the input signal through a dispersive channel. The channel estimation is implemented as a FIR filter, with the initial tap coefficients provided by the user. Ports Name and description Port type Signal type Supported Modes Input Input Electrical Sampled signals Output Output Electrical Sampled signals Parameters Main Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s [0, 1e100] Reference bit rate to use for the decision instant calculation and tap delays Samples per bit MBits/s GBits/s 8 — — [1, 1e100] True — — [1, 1000000] 1 a.u. — [-1e100, 1e100] 0 a.u. — [-1e100, 1e100] The number of samples per bit used by the equalizer Traceback length The number of bits, or trellis branches used in the Viterbi algorithm High level input (HLI) Value for the high level input modulation Low level input (LVI) Value for the low level input modulation 413 MLSE EQUALIZER FIR channel estimates Name and description Default value Default unit Units Value range Number of coefficients 8 — — [0, 10000] 1x2 — — [-1e+100,1e+100] FIR.dat — — — Default value Default unit Units Value range — — — — — — Default unit Units Value range Number of FIR coefficients that will be used in the calculation Coefficients real imag Table with real and imaginary part of complex coefficients Filename Filename with list of coefficients Preample Name and description Preamble vector Specifies the preamble that is expect to precede the data in the input signal Postamble vector Specifies the postamble that is expect to follow the data in the input signal Simulation Name and description Default value Enable True True, False Determines whether or not the component is enabled Technical background An electronic equalizer attempts to mitigate intersymbol interference (ISI) caused by time-dispersive channels, such as chromatic dispersion and polarization mode dispersion (PMD) in single mode fibers [1]. This component is a MLSE (maximum likelihood sequence estimate) electronic equalizer [2]. The component uses the Viterbi algorithm to equalize the input signal through a dispersive channel. The channel estimation is implemented as a FIR filter, with the initial tap coefficients provided by the user The signal input x(t) is resampled based on the parameters Reference bit rate and Samples per bit. The resampled signal is then filtered by the FIR filter using the channel coefficients. The number of coefficients must be a multiple of the number of samples per bit. If the number of coefficients is not a multiple the component will add 414 MLSE EQUALIZER zero value coefficients to the FIR filter until the number of coefficients is a multiple of the number of samples per bit. Figure 1 Equalizer schematic Parameters Low and High level input defines the constellation of the signal modulation. The user can provide the filter coefficients directly by using the parameter Coefficients real imag; alternatively the measurements can be loaded from a file using the parameter Filename. The real and imaginary part of the complex coefficients, or only the real part, must be provided in the file containing one column (real part only), or two columns, where the first one refers to the real part and the second one to the imaginary part of the complex coefficient. References: [1] F. Buchali, G. Thielecke, and H. Bulow, "Viterbi equalizer for mitigation of distortions from chromatic dispersion and PMD at 10 Gb/s," OFC'2004, vol.1, Paper MF-85, Feb. 2004. [2] J. G. Proakis, Digital Communications, 3rd ed. New York: McGraw-Hill, 1995. 415 MLSE EQUALIZER Notes: 416 INTEGRATE AND DUMP Integrate And Dump This component creates a cumulative sum of the discrete-time input signal. It also resets the sum to zero according to a user defined time period. Ports Name and description Port type Signal type Input Input Electrical Reset Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Reset threshold 0 a.u. — [-1e100, 1e100] 1 — — [-1e100, 1e100] 0 — — [-1e100, 1e100] False — — True, False True — — True, False 0 a.u. — [-1e100, 1e100] The reset signal amplitude that resets the integrator Feedback gain Gain of the feedback loop Initial state The initial value of the integrator before the calculation begins Limiter Determines whether or not the internal limiter is enabled Saturate Determines whether or not to saturate the signal Minimum amplitude Limiter’s minimum value 417 INTEGRATE AND DUMP Name and description Default value Default unit Units Value range Maximum amplitude 1 a.u. — [-1e100, 1e100] Name and description Default value Default unit Units Value range Enable True Limiter’s maximum value Simulation True, False Determines whether or not the component is enabled Technical background The Integrate and Dump component integrates the input signal in the specified time window. The following equation describes the integration process: S Out ( i ) = K ⋅ S Out ( i – 1 ) + S In ( i ) Where (1) S Out is the output signal, S In is the input signal, K is the Feedback gain parameter. The initial state of the integrator is defined by the Initial state parameter. The integration can be reset by the control signal, where the reset threshold parameter defines in which control signal value the integration will be reset. At each reset time, the component sends the result to the output port, and then clears the internal state for the next step of integration. There is the option to introduce limits to the output signal, which are defined by the parameters Minimum amplitude and Maximum amplitude. To introduce these limits the Limiter parameter has to be set to TRUE. In this case the output signal can be saturated or not when it reaches the limits. When the Saturation parameter is FALSE the component is reset every time the limit is reached. 418 IDEAL FREQUENCY DEMODULATOR Ideal Frequency Demodulator Converts the received optical signal phase into electrical signal amplitude. Ports Name and description Port type Signal type Input Input Optical Output Output Electrical Parameters Main Name and description Default value Units Value range Min. amplitude 0 a.u. ]-INF,+INF[ 1 a.u. ]-INF,+INF[ Minimum electrical signal amplitude at the output port Max. amplitude Maximum electrical signal amplitude at the output port Downsampling Name and description Default value Default unit Units Value range Centered at max power True — — True, False 193.1 THz Hz, THz, nm [30, 3e5] 5*(Sample rate) Hz Hz, GHz, THz, nm [0,+INF[ Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center frequency User-defined center frequency for the internal filter Sample rate Internal filter bandwidth 419 IDEAL FREQUENCY DEMODULATOR Polarization Name and description Default value Units Value range Polarization X — X, Y Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the frequency from the polarization X or Y of the optical signal will be converted to amplitude Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The incoming optical signal and noise bins are filtered by an ideal rectangle filter to reduce the number of samples in the electrical signal. The new sample rate is defined by the parameter Sample rate. You can define the center frequency, or it can be calculated automatically by centering the filter at the optical channels with maximum power. Optical noise bins are converted to gaussian noise inside the signal bandwidth. You must supply the polarization for the frequency extraction. The signal frequency is then normalized in the range between the parameters Min. and Max. amplitude. Figure 1 Filtered signal The converter resamples the signal and converts the noise bins. They are added in time domain. 420 IDEAL PHASE DEMODULATOR Ideal Phase Demodulator Converts the received optical signal phase into electrical signal amplitude. Ports Name and description Port type Signal type Input Input Optical Output Output Electrical Parameters Main Name and description Default value Units Value range Min. amplitude 0 a.u. [-1e+100, 1e+100] 1 a.u. [-1e+100, 1e+100] Minimum electrical signal amplitude at the output port Max. amplitude Maximum electrical signal amplitude at the output port Downsampling Name and description Default value Default unit Units Value range Centered at max power True — — True, False 193.1 THz Hz, THz, nm [30, 3e5] 5*(Sample rate) Hz Hz, GHz, THz, nm [0,+INF[ Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center frequency User-defined center frequency for the internal filter Sample rate Internal filter bandwidth 421 IDEAL PHASE DEMODULATOR Polarization Name and description Default value Units Value range Polarization X — X, Y Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the frequency from the polarization X or Y of the optical signal will be converted to amplitude Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The incoming optical signal and noise bins are filtered by an ideal rectangle filter to reduce the number of samples in the electrical signal. The new sample rate is defined by the parameter Sample rate. You can define the center frequency, or it can be calculated automatically by centering the filter at the optical channels with maximum power. Optical noise bins are converted to gaussian noise inside the signal bandwidth. You must supply the polarization for the phase extraction. The signal phase is then normalized in the range between the parameters Min. and Max. amplitude. Figure 1 Converted noise bins enabled The converter resamples the signal and converts the noise bins. They are added in time domain. 422 OPTICAL RECEIVER Optical Receiver This component is an optical receiver subsystem built using a PIN or APD photodetector, a Bessel filter and a 3R regenerator. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals, Noise bins Bit Sequence Output Binary Reference Output Electrical Output Output Electrical Default unit Units Parameters Main Name and description Default value Value range Photodetector PIN [PIN, APD] 3 [0, 1e+100] 0.9 [1e-100, 1] Select the photodetector type: PIN or APD Gain The avalanche gain for the photodetector APD Ionization ratio The ionization ratio for the photodetector APD Responsivity 1 A/W [0, 100] 10 nA [0, 1e+100] The responsivity of the photodetector Dark current The photodetector dark current 423 OPTICAL RECEIVER Low Pass Filter Name and description Default value Default unit Units Value range Cutoff frequency 0.75* bit rate Hz Hz, MHz, GHz [0, 1e+100] 0 dB [0, 1e+100] 100 dB [0, 1e+100] 3-dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order 4 [1, 100] Order of the function 3R Regenerator Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s, MBits/s, GBits/s [0, 1e+012] Reference bit rate to use for the decision instant calculation User defined delay NO [YES, NO] Defines whether the user can define the delay compensation Delay compensation 0 s Delay to apply to the signal input User defined decision NO s, ms, ns [-1e+100, 1e+100] [YES, NO] Defines whether the component will automatically calculate the decision instant or it will be defined by the user Decision instant 0.5 Bit [0, 1] Value for the decision instant to use when recovering the bit sequence User defined threshold NO [YES, NO] Defines whether the threshold will be automatically calculated or it will be user defined Absolute threshold Value for the threshold to use when recovering the bit sequence 424 0.5 a.u [-1e+100, 1e+100] OPTICAL RECEIVER Downsampling Name and description Default value Centered at max power YES Default unit Units Value range [YES, NO] Determines whether the internal filter will be centered at the maximum amplitude of the signal or it will be user defined Center frequency 193.1 THz Hz, THz, nm [30, 300000] 5* (Sample rate) Hz Hz, GHz, THz, nm [1, 1e+100] Name and description Default value Default unit Units Value range Noise calculation type Numerical Analytical, Numerical, Numerical convert noise bins Add signal-ASE noise YES [YES, NO] Add ASE-ASE noise YES [YES, NO] Add shot noise YES [YES, NO] Add thermal noise YES [YES, NO] Estimate receiver noise NO [YES, NO] User-defined center frequency of the internal filter Sample rate Sample rate of the signal output Noise Determines if shot noise is added to the signal Determines whether the receiver should estimate the thermal noise or not Thermal noise 1e-22 W/Hz Approximate sensitivity -18 dBm [-1e+100,0] 10 dB [0, 1e+100] W/Hz, A/Hz^.5 [0, 1e+100] The receiver sensitivity parameter Reference extinction ratio Reference extinction ratio used to measured the sensitivity Reference Q factor 6.4624 [0, 1000] Target Q factor for the current sensitivity 425 OPTICAL RECEIVER Random Numbers Name and description Default value Default unit Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background This component is an optical receiver subsystem. The subsystem was built using two different types of photodetectors, one Bessel filter and the 3R regenerator. The component properties allow the user to select the internal component parameters. Depending on the choice between PIN and APD, the Switch/Select components will redirect the signal into the proper photodetector type. Figure 1 Optical receiver example 426 SPATIAL OPTICAL RECEIVER Spatial Optical Receiver This component is an optical receiver subsystem built using the Spatial Aperture and the Optical Receiver components. The Optical receiver has a PIN or APD photodetector, a Bessel filter and a 3R regenerator. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals, Noise bins Bit Sequence Output Binary Reference Output Electrical Output Output Electrical Default unit Units Parameter Main Name and description Default value Aperture type Circular Value range [Circular, Square] Defines the aperture type Width 10 um [0, 1e+100] Defines the width of the square aperture or the diameter of the circular aperture Photodetector PIN [PIN, APD] 3 [0, 1e+100] Select the photodetector type: PIN or APD Gain The avalanche gain for the photodetector APD 427 SPATIAL OPTICAL RECEIVER Name and description Default value Ionization ratio 0.9 Default unit Units Value range [1e-100, 1] The Ionization ratio for the photodetector APD Responsivity 1 A/W [0, 100] 10 nA [0, 1e+100] Name and description Default value Default unit Units Value range Cutoff frequency 0.75* Bit rate Hz Hz, MHz, GHz [0, 1e+100] 0 dB [0, 1e+100] 100 dB [0, 1e+100] The responsivity of the photodetector Dark current The photodetector dark current Low Pass Filter 3-dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order 4 [1, 100] Order of the function 3R Regenerator Name and description Default value Default unit Units Value range Reference bit rate Bit rate Bits/s Bits/s, MBits/s, GBits/s [0, 1e+012] Reference bit rate to use for the decision instant calculation User defined delay NO [YES, NO] Defines whether the user can define the delay compensation Delay compensation 0 Delay to apply to the signal input User defined decision Defines whether the component will automatically calculate the decision instant or it will be defined by the user 428 NO s s, ms, ns [-1e+100, 1e+100] [YES, NO] SPATIAL OPTICAL RECEIVER Name and description Default value Default unit Decision instant 0.5 Bit Units Value range [0, 1] Value for the decision instant to use when recovering the bit sequence User defined threshold NO [YES, NO] Defines whether the threshold will be automatically calculated or it will be user defined Absolute threshold 0.5 (a, u) [-1e+100, 1e+100] value for the threshold to use when recovering the bit sequence Downsampling Name and description Default value Centered at max power YES Default unit Units Value range [YES, NO] Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user defined Center frequency 193.1 THz Hz, THz, nm [30, 300000] 5*(Sample rate) Hz Hz, GHz, THz, nm [0, 1e+100[ User-defined center frequency for the internal filter Sample rate Sample rate of the signal output Noise Name and description Default value Default unit Units Value range Noise calculation type Numerical Analytical, Numerical, Numerical convert noise bins Add signal-ASE noise YES [YES, NO] Add ASE-ASE noise YES [YES, NO] Add shot noise YES [YES, NO] YES [YES, NO] Determines if shot noise is added to the signal Add thermal noise 429 SPATIAL OPTICAL RECEIVER Name and description Default value Estimate receiver noise NO Default unit Units Value range [YES, NO] Determines whether the receiver should estimate the thermal noise or not Thermal noise 1e-22 W/Hz Approximate sensitivity -18 dBm [-1e+100,0] 10 dB [0, 1e+100] W/Hz, A/Hz^.5 [0, 1e+100] The receiver sensitivity parameter Reference extinction ratio Reference extinction ratio used to measured the sensitivity Reference Q factor 6.4624 [0, 1000] Target Q factor for the current sensitivity Random Numbers Name and description Default value Default unit Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random see index User-defined seed index for noise generation Technical background The layout of the Spatial Optical Receiver is presented in Figure 1. Refer to Spatial Aperture and Optical Receiver component documentation for the technical background of the models. Figure 1 430 Spatial Optical Receiver subsystem PHOTODETECTOR PIN Photodetector PIN PIN photodiode. Ports Name and description Port type Signal type Input Input Optical Output Output Electrical Parameters Main Name and description Default value Units Value range Responsivity 1 A/W [0,100] Dark current 10 nA [0,+INF[ Downsampling Name and description Default value Default unit Units Value range Centered at max power True — — True, False 193.1 THz Hz, THz, nm [30,3e5] 5*(Sample rate) Hz Hz, GHz, THz, nm [1e-3,+INF[ Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center frequency User-defined center frequency for the internal filter Sample rate 431 PHOTODETECTOR PIN Noise Name and description Default value Default unit Units Value range Noise calculation type Numerical — — Analytical, Numerical, Numerical Convert noise bins Add signal-ASE noise True — — True, False Add ASE-ASE noise True — — True, False Add thermal noise True — — True, False Thermal noise 0 W/Hz — [0,+INF[ Add shot noise True — — True, False Gaussian — — Poisson, Gaussian Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if shot noise is added to the signal Shot noise distribution Determines the distribution used to generate the shot noise Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 432 PHOTODETECTOR PIN Technical background The incoming optical signal and noise bins are filtered by an ideal rectangle filter to reduce the number of samples in the electrical signal. The new sample rate is defined by the parameter Sample rate. You can define the center frequency, or it can be calculated automatically by centering the filter at the optical channel with maximum power. If the noise calculation type in Numerical: Optical noise bins are converted to Gaussian noise inside of the signal bandwidth. The combined optical field is then converted to optical power. If the option Numerical — Convert Noise Bins is selected, the output noise and signal are combined. This means that you cannot see the separate contributions of the noise. However, if you select Numerical only, the signal and noise are separated and you can select the different contributions of the noise. Figure 1 Convert noise bins enabled The PIN resamples the signal and converts the noise bins when Convert Noise Bins is enabled. Gaussian shot noise distribution If the parameter Add shot noise is enabled and the Shot noise distribution parameter is Gaussian, the optical power is converted to electrical current by: (1) i ( t ) = i s ( t ) + i th ( t ) + i d + i sh ( t ) where is(t) is the optical signal calculated from the responsivity r: (2) i s ( t ) = rP s ( t ) where ith(t) is the thermal noise current calculated from the power spectral density defined by the parameter Thermal noise, and id is the dark current. 433 PHOTODETECTOR PIN The shot noise current ish(t) is calculated according to the power spectral density [1]: N sh = q ( i s + i d ) (3) Poisson shot noise distribution If the parameter Add shot noise is enabled and Shot noise distribution parameter is Poisson, the electrical current is calculated according to [2]: qn i ( t ) = --------e + i th ( t ) Δt (4) where ne denotes the number of electrons generated in the time instant Δt. The ⟨ n e⟩ (equal to the average number of detected photons) within the time interval Δt is given by: average number of generated electrons is ( t ) i ⟨ n e⟩ = --------- Δt + ---d- Δt . q q (5) The number of generated electrons n e is the Poisson random variable with mean and variance equal ⟨ n e⟩ . If the noise calculation type is Analytical: In this case, the signal and the noise components are calculated independently. The noise components are the variance and the noise PSD. Figure 2 Convert noise bins disabled In Figure 2, the PIN resamples the signal and does not convert the noise bins if Convert Noise Bins is disabled. 434 PHOTODETECTOR PIN The output electrical signal is: (6) i ( t ) = rP ( t ) + i d Note: This signal does not include the noise components. The noise components are calculated by the noise variance and by the power spectral density. For the noise variances: 2 2 (7) 2 σ ( t ) = σ sh ( t ) + σ s – ASE ( t ) 2 where σ sh ( t ) is the signal shot noise: 2 σ sh ( t ) = qi s ( t )B e where and (8) B e is the electrical bandwidth. 2 σ s – ASE ( t ) is the signal ASE beating: 2 2 (9) σ s – ASE ( t ) = 4r P ASE ( t )P s ( t ) For the noise PSD components: P ( f ) = P TH ( f ) + P ASE – ASE ( f ) + P ASEsh ( f ) (10) where PTH(f) is the thermal noise and PASE-ASE(f) is the beating of ASE-ASE: 2 P ASE – ASE ( f ) = r ( PASE ( f )∗ PASE ( f ) ) (11) and the ASE shot noise is: (12) P ASEsh ( f ) = qrP ASE ( f )B e Defining sensitivity The sensitivity of a receiver can be defined by optimizing the receiver parameters. A typical way of doing this is to optimize the thermal noise in your receiver, to obtain –9 a specific BER ( 1 × 10 ) . 435 PHOTODETECTOR PIN References: [1] Agrawal, G.P., Fiber-Optic Communication Systems. John Wiley & Sons, New York, (1997). [2] Jeruchim, M.C., Balaban, P., Shanmugan, K., Simulation of Communication Systems: Modeling, Methodology, and Techniques. Plenum Press, New York, (1997). 436 PHOTODETECTOR APD Photodetector APD Filter with a square cosine roll off frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Gain 3 — — [0,+INF[ Responsivity 1 A/W — [0,100] Ionization ratio 0.9 — — ]0,1] 10 nA — [0,+INF[ Name and description Default value Default unit Units Value range Centered at max power True — — True, False 193.1 THz Hz, THz, nm [30,3e5] Avalanche multiplication factor Ionization factor Dark current Dark current amplified by the avalanche effect Downsampling Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center frequency User-defined center frequency for the internal filter 437 PHOTODETECTOR APD Name and description Default value Default unit Units Value range Sample rate 5*(Sample rate) Hz Hz, GHz, THz, nm [1e-3,+INF[ Noise Name and description Default value Default unit Units Value range Noise calculation type Numerical — — Analytical, Numerical, Numerical Convert noise bins Add signal-ASE noise True — — True, False Add ASE-ASE noise True — — True, False Add thermal noise True — — True, False Thermal noise 0 W/Hz — [0,+INF[ Add shot noise True — — True, False Gaussian — — [WMC, Gaussian] Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if shot noise is added to the signal Shot noise distribution Determines the distribution used to generate the shot noise Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background The incoming optical signal and noise bins are filtered by an ideal rectangle filter to reduce the number of samples in the electrical signal. The new sample rate is defined by the parameter Sample rate. You can define the center frequency, or it can be calculated automatically by centering the filter at the optical channel with maximum power. 438 PHOTODETECTOR APD If the noise calculation type in Numerical: Optical noise bins are converted to Gaussian noise inside of the signal bandwidth. The combined optical field is then converted to optical power. If the option Numerical — Convert Noise Bins is selected, the output noise and signal are combined. This means that you cannot see the separate contributions of the noise. However, if you select Numerical only, the signal and noise are separated and you can select the different contributions of the noise. Figure 1 Convert noise bins enabled The APD resamples the signal and converts the noise bins when Convert Noise Bins is enabled. If the parameter Add shot noise is enabled and Shot noise distribution parameter is Gaussian, the optical power is converted to electrical current: (1) i ( t ) = i s ( t ) + i th ( t ) + i d + i sh ( t ) where is(t) is the optical signal calculated from the responsivity r and the gain M as: (2) i s ( t ) = MrP s ( t ) and ith(t) is the thermal noise current calculated from the power spectral density defined by the parameter Thermal noise and id is the additive dark current. The shot noise current ish(t) is calculated according to the power spectral density: 2 (3) N sh ( t ) = qM F ( rP s ( t ) + i dm ) where idm is the dark current and F depends on M: (4) F ( M ) = kM + ( 2 – 1 ⁄ M ) ( 1 – k ) where k is the Ionization ratio. 439 PHOTODETECTOR APD If the noise calculation type is Analytical: In this case, the signal and the noise components are calculated independently. The noise components are the variance in time and the noise PSD. Figure 2 Convert noise bins disabled The PIN resamples the signal and does not convert the noise bins if Convert Noise Bins is disabled. The output electrical signal is: i ( t ) = rP ( t ) + i d (5) The noise variances are: 2 2 2 σ ( t ) = σ sh ( t ) + σ s – ASE ( t ) (6) 2 where σ sh ( t ) is the signal shot noise: 2 2 σ sh ( t ) = qM Fi s ( t )Be where (7) B e is the electrical bandwidth. 2 and σ s – ASE ( t ) is the signal ASE beating: 2 2 2 σ s – ASE ( t ) = 4r M P ASE ( t )P s ( t ) 440 (8) PHOTODETECTOR APD The noise PSD components are: P ( f ) = P TH ( f ) + P ASE – ASE ( f ) + P ASEsh ( f ) (9) where PTH(f) is the thermal noise and PASE-ASE(f) is the beating of ASE-ASE: 2 2 P ASE – ASE ( f ) = r M ( P ASE ( f )∗ P ASE ( f ) ) (10) and the ASE shot noise is: 2 (11) PASEsh ( f ) = qM FrP ASE ( f )B e Reference: [1] Agrawal, G.P., Fiber-Optic Communication Systems. John Wiley & Sons, New York, (1997). 441 PHOTODETECTOR APD Notes: 442 SPATIAL PIN PHOTODETECTOR Spatial PIN Photodetector This component is PIN photodetector that include spatial effects. It is a subsystem built using the Spatial Aperture component followed by the PIN photodetector. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals, Noise bins Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Aperture type Circular Width 10 um [0, 1e+100] 1 A/W [0, 100] 10 nA [0, 1e+100] [Circular, Square] Defines the width of the square aperture or the diameter of the circular aperture Responsivity The responsivity of the photodetector Dark current The photodetector dark current 443 SPATIAL PIN PHOTODETECTOR Downsampling Name and description Default value Centered at max power YES Default unit Units Value range [YES, NO] Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user defined Center frequency 193.1 THz Hz, THz, nm [30, 300000] 5* (Sample rate) Hz Hz, GHz, THz, nm [1, 1e+100] User-defined center frequency of the internal filter Sample rate Sample rate of the signal output Noise Name and description Default value Default unit Noise calculation type Numerical Analytical, Numerical, Numerical Convert noise bins Add signal-ASE noise YES [YES, NO] Add ASE-ASE noise YES [YES, NO] Add thermal noise YES [YES, NO] Thermal noise 1e-22 Add shot noise YES [YES, NO] Gaussian [Poisson, Gaussian] W/Hz Units W/Hz, A/Hz^.5 Value range [0, 1e+100] Determines if shot noise is added to the signal Shot noise distribution 444 SPATIAL PIN PHOTODETECTOR Random numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The layout of the Spatial PIN Photodetector is presented in Figure 1. Refer to Spatial Aperture and Photodetector PIN component documentation for the technical background of the models. Figure 1 Spatial PIN Photodetector subsystem 445 SPATIAL PIN PHOTODETECTOR Notes: 446 SPATIAL APD PHOTODETECTOR Spatial APD Photodetector This component is APD photodetector that include spatial effects. It is a subsystem built using the Spatial Aperture component followed by the APD photodetector. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sampled signals, Noise bins Output Output Electrical Parameters Main Name and description Default value Aperture type Circular Width 10 Default unit Units Value range [Circular, Square] um [0, 1e+100] Defines the width of the square aperture or the diameter of the circular aperture Gain 3 [0, 1e+100] The avalanche gain Responsivity 1 A/W [0, 100] The responsivity of the photodetector Ionization ratio 0.9 [1e-100, 1] The ionization ratio Dark current 10 nA [0, 1e+100] The photodetector dark current 447 SPATIAL APD PHOTODETECTOR Downsampling Name and description Default value Centered at max power YES Default unit Units Value range [YES, NO] Determines whether the internal filter will be centered at the maximum amplitude of the signal or if it will be user-defined Center frequency 193.1 THz Hz, THz, nm [30, 300000] 5* (Sample rate) Hz Hz, GHz, THz, nm [1, 1e+100] User-defined center frequency of the internal filter Sample rate Sample rate of the signal output Noise Name and description Default value Default unit Noise calculation type Numerical Analytical, Numerical, Numerical Convert noise bins Add signal-ASE noise YES [YES, NO] Add ASE-ASE noise YES [YES, NO] Add thermal noise YES [YES, NO] Thermal noise 1e-22 Add shot noise YES [YES, NO] Gaussian [WMC, Gaussian] W/Hz Units W/Hz, A/Hz^.5 Value range [0, 1e+100] Determines if shot noise is added to the signal Shot noise distribution 448 SPATIAL APD PHOTODETECTOR Random numbers Name and description Default value Units Value range Generate random seed YES [YES, NO] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The layout of the Spatial APD Photodetector is presented in Figure 1. Refer to Spatial Aperture and Photodetector APD component documentation for the technical background of the models. Figure 1 Spatial APD Photodetector subsystem 449 SPATIAL APD PHOTODETECTOR Notes: 450 Amplifiers Library This section contains information on the following amplifiers. Optical Raman • Raman Amplifier—Average Power Model • Raman Amplifier—Dynamic Model EDFA • EDFA Black Box • EDF Dynamic-Full Model • EDF Dynamic—Analytical Model • EDFA • Optical Amplifier • EDFA Measured • Erbium Doped Fiber • Er-Yb Codoped Fiber • Er-Yb Codoped Fiber Dynamic • Er-Yb Codoped Waveguide Amplifier • Yb-Doped Fiber • Yb-Doped Fiber Dynamic SOA • Traveling Wave SOA • Wideband Traveling Wave SOA • Reflective SOA 451 AMPLIFIERS LIBRARY Electrical 452 • Limiting Amplifier • Electrical Amplifier • Transimpedance Amplifier • AGC Amplifier RAMAN AMPLIFIER COMPONENT (OBSOLETE) Raman Amplifier Component (Obsolete) This component is an obsolete version that is included with OptiSystem for backwards compatibility purposes - It was replaced by the Bidirectional Optical Fiber component. Ports Name and description Port type Signal type Input 1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical Parameters Fiber Name and description Default value Default unit Value range Fiber length 10 km [0, INF] Attenuation data type Constant — Constant, Wavelength Dependent /From File Attenuation – constant 0.25 dB/km [0, INF] Attenuation vs. wavelength AtnVsLambda.dat — [0, INF] Forward Input Coupling Loss 1 dB [0, 106] Forward Output Coupling Loss 0.022 dB [0, 106] Backward Input Coupling Loss 1 dB [0, 106] Backward Output Coupling Loss 0.022 dB [0, 106] Effective area data type Constant — Constant, Wavelength Dependent/From File Effective area – constant 72 µm2 [0, INF] Effective area vs. wavelength EffAreaVsLambda.dat — [0, INF] 453 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Raman effect Name and description Default value Default unit Value range Peak Raman gain coef 9.9e-14 m/W [0, INF] Pump wavelength of peak Raman gain coef 1000 nm [0, INF] Raman gain spectrum vs. freq. RamanGainVsFreq.dat — — Raman gain polarization factor 0.5 — [0, INF] Temperature 300 K [0, INF] Name and description Default value Unit Value range Rayleigh coef. data type Constant — Constant, Wavelength Dependent/From File Rayleigh coef. — constant 5e-005 1/km [0, INF] Rayleigh coef. vs. wavelength RayleighGainvsLambda.dat — [0, INF] Name and description Default value Unit Value range Left end reflection data type Constant — Constant, Wavelength Dependent/From File Left end reflection — constant –30 dB [-INF, 0] Left end reflection vs. wavelength NearEndReflVsLambda.dat — [-INF, 0] Right end reflection data type Constant — Constant, Wavelength Dependent/From File Right end reflection — constant –30 dB [-INF, 0] Right end reflection vs. wavelength FarEndReflVsLambda. dat — [-INF, 0] Rayleigh effect Reflections 454 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Other nonlinearities Name and description Default value Unit Value range Brillouin gain coef 5e-011 m/W [0, INF] Brillouin bandwidth data type Constant — Constant, Wavelength Dependent/From File Brillouin bandwidth — constant 40 MHz [0, INF] Brillouin bandwidth vs. wavelength FarEndReflVsLambda.dat — [0, INF] Brillouin Stokes shift 11 GHz [0, INF] Nonlinear refr. index data type Constant — Constant, Wavelength Dependent/From File Nonlinear refr. index — constant 3e-020 m2/W [0, INF] Nonlinear refr. index vs. wavelength N2VsLambda.dat — [0, INF] Raman-resonant n2 dispersion RealHiRezVsLambda.dat — [–INF, INF] Eff. refr. index vs. wavelength EffRIVsLambda.dat — [0, INF] Group velocity dispersion 5 ps/nm/km [0, INF] Dispersion slope 0.1 ps/nm2/km [0, INF] Effects on/off Name and description Value range Dependence Attenuation ON [ON, OFF] Rayleigh backscattering gain ON [ON, OFF] SRS gain ON [ON, OFF] OFF [ON, OFF] Pump depletion in SRS ON [ON, OFF] Double Rayleigh scattering OFF [ON, OFF] Left end reflection OFF [ON, OFF] Right end reflection OFF [ON, OFF] Polarisation maintaining fiber OFF [ON, OFF] (Stimulated Raman scattering gain) SpRS gain Spontaneous Raman scattering gain) 455 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Simulation details Name and description Default value Unit Value range Enable ON — [ON, OFF] Parameter set Default — Default, Auto, User Upper Pump wavelength 1450 nm [0, INF] Power accuracy 0.001 — [0, INF] Max. number of iterations 100 — [1, 10000] Number of power iterations 4 — [1, 10000] ODE integration method 5th-order Runge-Kutta with step size control — 5th-order Runge-Kutta with step size control, Gear's stiff eq. solver with step size control ODE integrator accuracy 1e-006 — [0, 1] Max. number of steps per iteration 100000 — [1, 10000] Number of longitudinal points 256 — [10, 100000] Background noise PSD level 1e-100 W/Hz [0, 10000] Inphase noise ratio 0 — [0, 1] Calculate 3D graphics ON — [ON,OFF] 3D graphics resolution 10 — [1, 100] Noises Name and description Default value Default unit Unit Value range Noise center frequency 193.1 THz Hz, THz, nm [30, 3e+006] Noise bandwidth 30 THz Hz, THz, nm [0, INF] Noise bins spacing 1000 GHz Hz, GHz, THz, nm [0, INF] Noise threshold –100 dB — [-INF,+INF] Noise dynamic 3 dB — [0, INF] Convert noise bins Convert noise bins — — [ON, OFF] 456 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Random numbers Name and description Default value Unit Value range Generate random seed ON — [ON,OFF] 0 — [0, 4999] Name and description Default value Unit Value range Lower limit of Region of Interest 1550 nm [0, INF] Upper limit of Region of Interest 1600 nm [0, INF] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Results 457 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Graphs Name and description X Title Y Title Wavelength [nm] Power [dBm] Forward Output Gain [dB] Wavelength [nm] Gain [dB] Forward Output OSNR [dB] Wavelength [nm] OSNR [dB] Forward Output Multiple Rayleigh Scattering Spectrum [dBm] Wavelength [nm] Power [dBm] Backward Output Power Spectrum [dBm] Wavelength [nm] Power [dBm] Backward Output Gain [dB] Wavelength [nm] Gain [dB] Backward Output OSNR [dB] Wavelength [nm] OSNR [dB] Backward Output Multiple Rayleigh Scattering Spectrum [dBm] Wavelength [nm] Power [dBm] Forward Power Spectrum [dBm] Wavelength [nm] Fiber Length [km] Forward Gain [dB] Wavelength [nm] Fiber Length [km] Forward Gain Coefficient [dB/km] Wavelength [nm] Fiber Length [km] Forward OSNR [dB] Wavelength [nm] Fiber Length [km] Forward Double Rayleigh Scatt. Spectrum [dBm] Wavelength [nm] Fiber Length [km] Backward Power Spectrum [dBm] Wavelength [nm] Fiber Length [km] Backward Gain [dB] Wavelength [nm] Fiber Length [km] Backward Gain Coefficient [dB/km] Wavelength [nm] Fiber Length [km] Backward OSNR [dB] Wavelength [nm] Fiber Length [km] Backward Double Rayleigh Scatt. Spectrum [dBm] Wavelength [nm] Fiber Length [km] Forward Output Power Spectrum [dBm] When a parameter is defined as a curve loaded from a file, the format of the file is: Wavelength_1 ParameterValue_1 Wavelength_2 ParameterValue_2 Wavelength_3 ParameterValue_3 ...... Wavelength_N ParameterValue_N The unit of the wavelengths is always [nm]. The units of the parameter values are given in the table above, and are the same as the units of the respective Constant parameter. Arbitrary number of points (file lines) are allowed, except 0 (empty file). 458 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Results The component produces the following results: • Maximum Forward Gain [dB] • Maximum Forward On/Off Gain [dB] • Forward Gain Flatness [dB] • Maximum Forward Power [dB] • Wavelength of Maximum Forward Power [dB] • Minimum Forward Effective Noise Figure [dB] • Forward Effective Noise Figure Flatness [dB] • Maximum Backward Gain [dB] • Maximum Backward On/Off Gain [dB] • Backward Gain Flatness [dB] • Maximum Backward Power [dB] • Wavelength of Maximum Backward Power [dB] • Minimum Backward Effective Noise Figure [dB] • Backward Effective Noise Figure Flatness [dB] These results are calculated for the wavelength range defined in the Results tab of the Component Properties dialog box. Forward and Backward are names used to distinguish the characteristics pertaining to the left and right ends of the fiber respectively. They have nothing to do with the frequently used terms forward / (backward) Raman amplification, meaning amplifier configuration having co-propagating / (counter-propagating) pump and signals. Graphics The Raman Amplifier presents the results of the calculations in a variety of both 2D and 3D graphics. 2D graphics The following 2D graphs are available: • Forward Output Power Spectrum [dBm] • Forward Output Gain [dB] • Forward Output On/Off Gain [dB] • Forward Output OSNR [dB] • Forward Double Rayleigh Scattering Spectrum [dBm] • Forward Eff. Noise Figure Spectrum [dB] • Backward Output Power Spectrum [dBm] 459 RAMAN AMPLIFIER COMPONENT (OBSOLETE) • Backward Output Gain [dB] • Backward Output On/Off Gain [dB] • Backward Output OSNR [dB] • Backward Double Rayleigh Scattering Spectrum [dBm] • Backward Eff. Noise Figure Spectrum [dB] 3D graphics The following 3D graphs are available: • Forward Power Spectrum [dBm] • Forward Gain [dB] • Forward Gain Coefficient [dB/km] • Forward OSNR [dB] • Forward Double Rayleigh Scattering Spectrum [dBm] • Backward Power Spectrum [dBm] • Backward Gain [dB] • Backward Gain Coefficient [dB/km] • Backward OSNR [dB] • Backward Double Rayleigh Scattering Spectrum [dBm] 2D/3D graphics The following 2D/3D graphics are available: • Forward Power Spectrum [dBm] • Forward On/Off Gain [dB] • Forward Gain [dB] • Forward Gain Coefficient [dB/km] • Forward OSNR [dB] • Forward Double Rayleigh Scattering Spectrum Power [dBm] • Forward Eff. Noise Figure [dB] • Backward Power Spectrum [dBm] • Backward On/Off Gain [dB] • Backward Gain [dB] • Backward Gain Coefficient [dB/km] • Backward OSNR [dB] • Backward Double Rayleigh Scattering Spectrum Power [dBm] • Backward Eff. Noise Figure [dB] Forward and Backward are names used to distinguish the characteristics pertaining to the overall optical spectra propagating from the left end to the right end of the fiber respectively, and vice-versa. They have nothing to do with the frequently used terms 460 RAMAN AMPLIFIER COMPONENT (OBSOLETE) forward / (backward) Raman amplification, meaning amplifier configuration having co-propagating / (counter-propagating) pump and signals. Technical background Introduction The most promising technology to support almost unlimited bandwidth employs the nonlinear effect of stimulated Raman scattering (SRS) in hybrid EDFA + Raman fiber amplifiers (HRA) or purely Raman fiber amplifiers (RFA) [1,2]. The most important advantage of this effect is that the pump wavelength λp does not need to be tied to a particular energy level/absorption band, as it is in EDFAs. Raman amplification is readily obtainable in any spectral region and in any type of fiber, provided a practical pump source with wavelength 80-100 nm shorter than that of the signal and with sufficiently high power is available. Given the progress in the manufacturing of highpower pump lasers in the infrared [3] along with the seemingly limitless demand for amplification bandwidth, Raman amplification will play an increasingly important role in WDM networks. SRS is among the best-understood third-order nonlinear processes, observed experimentally for the first time in 1962 in bulk media [4] and in 1972 in optical fibers [5]. It manifests itself as an exponential growth of a signal (Stokes) wave in the field of a shorter wavelength-intensive pump. As mentioned above, SRS is a non-resonant effect with respect to pump wavelength, which may lie anywhere in the transparency windows of the medium. On the other hand, the frequency difference ωp-ωs between the pump and signal waves should be resonant with one of the vibrational modes ωR of the host. SRS does not require phase-matching, and for CW pumps, it allows both forward (pump and signal co-propagating) and backward (counter-propagating) pumping configurations. The most important characteristics of SRS in telecom-grade fibers are [6 (and references)]: • The SRS gain spectrum peaks at 13.2 THz (≈ 100 nm at λp =1.55 μm), but extends up to 30 THz. • The 3dB bandwidth of the gain spectrum is 6-7 THz (≈ 50 nm at λp =1.55 μm). • The peak gain gRpeak (λ) coefficient is 6.4x10-13 m/W for λp = 1.55 [μm], and is inversely proportional to λp. • Both the shape of the spectrum and the value of gRpeak (λ) depend on the concentration of the dopants; the peak gain coefficient of pure GeO2 is 8 times larger than that of fused silica. Figure 1 shows the zero temperature Raman gain coefficient spectra of pure fused silica, pure fused GeO2, and silica doped with 25 mol.% GeO2. The spectra are scaled to the peak gain coefficient of silica. • The SRS effect is in principle highly polarization-dependent. Raman gain is negligible for orthogonal polarizations of the pump and signal. However, in nonpolarization maintaining fibers, the gain becomes polarization independent due to mode-scrambling. In this case gRpeak(λ) is reduced by a factor of 2. 461 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Figure 1 Zero temperature Raman coefficient spectra The arbitrary choice of pump(s) wavelength(s) allows for a key new feature in all types of hybrid and Raman fiber amplifiers: the possibility to arrange several pumps in a finite pump band and to amplify the WDM signals in their extended aggregate gain spectrum. Gain-equalization is achieved by a proper choice of the wavelengths and powers of the individual pumps. On the device level, the HRA and FRA come in a variety of configurations: backward-, forward- and bidirectionally pumped, discrete or distributed, single- or multi-stage. The ubiquitous nature of the Raman effect allows numerous types of fibers to be used as the SRS–active media — from standard transmission fibers in distributed FRA to short (5-8 km) DCFs or highly nonlinear heavily-doped fibers with small effective areas [9]. Typically, several hundred milliwatts of pump power are required. The challenges in modeling and optimizing FRAs are related mainly to the nonlinear, inefficient nature of SRS, requiring high pump powers and long fibers, and to the different pump mechanism. • All participating optical waves interact with each other. The shorter wavelengths transfer power to the longer wavelengths (all long wavelengths deplete all short wavelengths), resulting in a complex longitudinal distribution of gain coefficients and noise powers. • Other third-order nonlinear processes among the pumps take place — SPM and XPM, FWM, and stimulated Brillouin scattering (SBS). • Considerable noise powers and crosstalk are generated by multi-path Rayleigh scattering. An additional challenge is the requirement to build a model that is both quantitatively and qualitatively precise. While the general features of any of the effects above are well known [6], it is the complex interplay of the details that matters if such a model is 462 RAMAN AMPLIFIER COMPONENT (OBSOLETE) to be used as a versatile design tool by the photonics industry. As a result, some of the simplifications (usually found in the literature) should be rejected: • The Raman spectrum of pure fused silica must be used with care. For discrete FRAs, the magnitude and the spectrum of the Raman gain coefficient must always be defined in dependence on the concentration of the dopants [14]. The dispersion of the real part of the Raman-resonant nonlinear susceptibility must also be accounted for [15]. • The assumption that the fiber parameters, such as effective areas/overlap integrals, losses, and Brillouin gain bandwidth, are constants. In the wavelength region of 1.4-1.65 [μm], the effective areas of SMF-28TM and a typical DSF vary by 25% and 50% respectively. The comprehensive model described here uses the unified spectral signal representation illustrated in Figure 2. It features arbitrary number and location of pumps, signals and ASE bands, and complete forward / backward symmetry. Each forward propagating wave has a backward counterpart at the same wavelength and vice-versa. Figure 2 Unified spectral signal representation 463 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Formulation of the model As an example, the power and the phase change of any type of wave (pump, signal, or ASE) with central carrier frequency ωk as PF,B(z, ωk) and θF,B (z, ωk) respectively, where the subscripts F and B discriminate against the forward and backward propagating waves at the same wavelength. The system of coupled differential equations describing the operation of a FRA or the Raman sub-unit of a HRA has the form: dP F ( z ,ω k ) ------------------------- = – α ( ω k )P F ( z ,ω k ) dz + ρ ( ω k )P B ( z ,ω k ) N R ∑ + sp g ( ω k ,ω 1 ) [ P F ( z ,ω 1 ) + P B ( z ,ω 1 ) ] [ P F ( z ,ω k ) + P ( ω 1 ,ω k ,T ,Bk ) ] l = k+1 k–1 R – ∑ g ( ω l ,ω k ) [ P F ( z ,ω l ) + P B ( z ,ω l ) ]P F ( z ,ω k ) l=1 sp – 2F total ( ω k ,T )P F ( z ,ω k ) Br Br Br sp Br B + ------------------------g P B ( z ,ω k + Δω ) [ P F ( z ,ω k ) + P ( ω k + Δω ,ω k ,T ,Bk ) ] Br ( B + Bk ) Br Br Br sp Br B – ------------------------g [ P B ( z ,ω k – Δω ) + P ( ω k ,ω k – Δω ,T ,B k ) ]P F ( z ,ω k ) Br ( B + Bk ) N +∑ N N ∑ ∑ {g R ( ω k ,ω l ,ω m ,ω n ) cos [ Ψ ( z ) ] – 4γ ( ω k ,ω l ,ω m ,ω n ) sin [ Ψ ( z ) ] } l = 1m = 1n = 1 ωk = ωl + ωm – ωn x ( P F ( z ,ω k )P F ( z ,ω l ) )P F ( z ,ω m )P F ( z ,ω n ) 464 RAMAN AMPLIFIER COMPONENT (OBSOLETE) dθ F ( z ,ω k ) ------------------------- = dz N ∑ γ ( ωk ,ωl ,ωk ,ωl ) [ ( 2 – δkl )PF ( z ,ωl ) + 2PB ( z ,ωl ) ] l=1 R g ( ω k ,ω l ,ω m ,ω n ) ⎧ + ∑ ∑ ∑ ⎨ 2γ ( ω k ,ω l ,ω m ,ω n ) cos [ Ψ ( z ) ] + -----------------------------------------sin [ Ψ ( z ) ] 2 ⎩ l = 1m = 1n = 1 N ω k N N = ωl + ω m – ωn P F ( z ,ω l )P F ( z ,ω m )P F ( z ,ω n ) X ------------------------------------------------------------------P F ( z ,ω k ) The equations describing the evolution of P B ( z ,ωk ) and θ B ( z ,ωk ) are obtained by alternative interchanging of subscripts F and B. The notations are explained in Table 1. Table 1 Description of notations Notation Description N Number or pumps+signals+ASE bands in each direction 2N Total number of interacting waves α ( ωk ) Total losses ρ ( ωk ) Rayleigh scattering coefficient R R R g ( ω k ,ω 1 ) = f ( ω k ,ω 1 )g peak ( ω 1 )g norm ( ω 1 – ω k ) Raman gain coefficient R Peak Raman gain coefficient, depending on the frequency of the current pump wave. In fused silica, it is downshifted by Δω = ω R = 13.2 THz from the respective pump. g norm ( Δω ) R Normalized Raman gain spectrum of the fiber, as dependent on the type and concentration of the dopant. f ( ω l ,ω k ) ;f ( ω k ,ω l ,ω m ,ω n ) Mode overlap integrals; for definitions see, for example [6] (chap. 7 and 10) g peak ( ω 1 ) 465 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Notation Description sp P ( ω l ,ω k ,T ,B ) = h ( ω1 – ωk ) ⎧ --------------------------⎪ KT = 2hω k B ⎨ 1 + 1 ⁄ e –1 ⎪ ⎩ ⎫ ⎪ ⎬ ⎪ ⎭ sp F total ( ω k ,T ) = ωk 2πhω k ∫ 0 Power generated by spontaneous Raman and Brillouin scattering of the wave with carrier frequency ω 1 into the bandwidth of the wave with carrier ω k . Although the forms of these terms are identical, their values are different: sp P ( ω 1 ,ω k ,T ,B ) ≈ 2hω k B for SpRS, while sp P ( ω 1 ,ω k ,T ,B ) » 2hω k B for SpBS. A factor (with dimension of length) determining the integrated total power lost by the current wave via spontaneous Raman scattering into all possible lower frequencies, as depending on the Raman spectrum and the temperature. h (ωk – ω ) ⎧ ⎫ ------------------------⎪ ⎪ KT g ( ω ,ω k ) ⎨ 1 + 1 ⁄ e – 1 ⎬dω ⎪ ⎪ ⎩ ⎭ R B Bandwidth of the respective wave. h, K, T Planck bar constant, Boltzmann constant, Temperature. gBr, BBr, Δω Br Brillouin gain coefficient, line width, and Stokes shift. Ψ ( z ) = θ 1 ( z ) + θ m ( z ) – θ n ( z ) – θ k ( z ) – Δk .z Total phase difference between the nonlinearly mixed waves Δk Input phase mismatch δ lm Kroneker delta 466 RAMAN AMPLIFIER COMPONENT (OBSOLETE) References: [1] H. Masuda, S. Kawai, IEEE Photonics Technology Letters, Vol. 11, p. 647, 1999. [2] T. Nielsen, P. Hansen, A. Stentz, M. Aquaro, J. Pedrazzani, A. Abramov, and R. Espindola, IEEE Photonics Technology Letters, Vol. 10, p. 1492, 1998. [3] Laser Focus World, January 2000; SDL Press Release, http://www.sdli.com/investor/releases/19990630_BROADENS.html [4] E. Woodbury and W. Ng, Proc. IRE, Vol. 50, p. 2347, 1962. [5] R. Stolen, E. Ippen, and A. Tynes, Applied Physics Letters, Vol. 20, p. 62, 1972. [6] G. Agrawal, “Nonlinear Fiber Optics,” 2nd Edition, Academic Press Inc., San Diego, California, 1995. [7] F.L. Galeener, J.C. Mikkelsen Jr., R.H. Geils, and W.J. Mosby, Applied Physics Letters, Vol. 32, p. 34, 1978. [8] Y. Emori, K. Tanaka, and S. Namiki, Electronics Letters, Vol. 35, p. 1355, 1999. [9] T. Hosaka, S. Sudo, H. Itoh, and K. Okamoto, Electronics Letters, Vol. 24, p. 770, 1988. [10] H. Kidorf, K. Rottwitt, M. Nissov, M. Ma, and E. Rabarijaona, IEEE Photonics Technology Letters, Vol. 11, p. 530, 1999. [11] M. Nissov, K. Rottwitt, H. Kidorf, and M. Ma, Electronics Letters, Vol. 35, p. 997, 1999. [12] Y. Chen, Journal of the Optical Society of America, Vol. B7, p. 43, 1990. [13] B. Foley, M. Dakss, R. Davies, and P. Melman, Journal of Lightwave Technology, Vol. 7, p. 2024, 1989. [14] S. Davey, D. Williams, B. Ainslie, W. Rothwell, and B. Wakefield, IEE Proceedings, Vol. 136, p. 301, 1989. [15] R. Hellwarth, Progress of Quantum Electronics, Vol.5 , p. 1, 1977. [16] Y. Shen, “The Principles of Nonlinear optics,” J. Wiley & Sons Inc., 1984. [17] A. Uchida, M. Takeoka, T. Nakata, and F. Kannari, Journal of Lightwave Technology, Vol. 16, p. 92, 1998. [18] S. Evangelides, L. Mollenauer, J. Gordon, and N. Bergano, Journal of Lightwave Technology, Vol. 10, p. 28, 1992. 467 RAMAN AMPLIFIER COMPONENT (OBSOLETE) Notes: 468 RAMAN AMPLIFIER—AVERAGE POWER MODEL Raman Amplifier—Average Power Model This component simulates a Raman amplifier based on the average power approach [1], [2]. Ports Name and description Port type Signal type Input 1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical Parameters Main Name and description Symbo l Default value Default unit Value range Length L 10 km ]0; 1,000,000[ Constant — Constant, From File α 0.2 dB/km [0,+INF[ - FiberLoss.dat nm - dB/km - - Constant — Constant, From File Amplifier length. Attenuation data type Defines if attenuation is entered as scalar, used for all wavelengths, or if it is wavelength dependent / downloaded from a file. Attenuation Constant attenuation value Attenuation file Attenuation value dependent on wavelength. Effective area data type Defines if effective area is entered as scalar, used for all wavelengths, or if it is wavelength dependent/ downloaded from a file. 469 RAMAN AMPLIFIER—AVERAGE POWER MODEL Name and description Symbo l Default value Default unit Value range Effective interaction area A eff 72 µm2 [0, INF[ - EffectiveArea.dat nm - µm2 - - Raman gain - Raman gain, Raman gain efficiency - 1e-013 - [0,+INF[ - 1000 nm [0,+INF[ gr RG.dat THZ normalized Raman gain - Name and description Symbo l Default value Default unit Value range Temperature T 300 K [0,500] K eff 2 - [1,2] Constant effective area. Effective interaction area file Effective area dependent on wavelength. Raman gain type Defines type of Raman gain. If Raman gain efficiency is selected, effective area is disabled, and value is g r / Aeff . Otherwise, it is normalized g r multiplied by Raman gain peak (see below). Raman gain peak Normalized Raman gain is multiplied by Raman gain peak. Formula is detailed later in this section. Raman gain reference pump Value used for Raman gain calculation. Formula is detailed later in this section. Gain X frequency File that defines Raman gain or the Raman gain efficiency. Enhanced Absolute temperature at which fiber is operating. Used for noise consideration. Polarization factor Actual value depends on relative polarization of fields of channels i and j. Equals 1 if fields of both channels are polarization-aligned, and 2 for totally scrambled polarization [4]. 470 RAMAN AMPLIFIER—AVERAGE POWER MODEL Name and description Symbo l Default value Default unit Value range Rayleigh back scattering data type - Constant - Constant, From File γ- 5.0e-005 1/km [0, INF[ - Rayleigh.dat nm - 1/km - - 1450 nm [0,3000] - False - True, False - 16.75 ps/nm/km ]-INF,+INF[ - 0.075 ps/nm2/km ]-INF,+INF[ - 1550 nm [100,2000] Defines whether Rayleigh back scattering coefficient is entered as scalar, used for all wavelengths, or wavelength dependent/downloaded from a file. Rayleigh back scattering Constant Rayleigh back scattering. Rayleigh back scattering file Rayleigh back scattering dependent on wavelength. Upper pump reference Used for convergence test. All wavelengths below this value are considered pump, and are not taken into account for the convergence test. Enable dispersion Enables the linear chromatic dispersion application for the signals. Dispersion Value of the GVD (Group Velocity Dispersion) parameter in wavelength domain. Dispersion slope Value of the dispersion slope parameter. Reference wavelength Used internally as “zero” (or reference) frequency in spectrum of signal envelope. Attenuation value is assumed to correspond to this frequency. Numerical Name and description Default value Unit Value range Tolerance 0.01 - ]0,+INF[ Used to check convergence of the model. Based on gain of the signals. 471 RAMAN AMPLIFIER—AVERAGE POWER MODEL Name and description Default value Unit Value range Number of divisions 50 - [1;50,000] 50 - [1;50,000] All signals - All signals, First signal Number of divisions (in space) of the fiber. Number of iterations Maximum number of iterations executed. If convergence is not reached in this number of iterations, model returns the calculated values anyway. Check convergence using: Defines if convergence is checked using “All signals” or “First signal”. Graphs Name and description Default value Unit Value range Calculate graphs False - True, False 20 - [1,1e8] 20 - [1,1e8] True - True, False -50 dBm ]-INF,+INF[ Defines if graphs are calculated or not. If False, component graphs are not represented. Number of distance steps Number of distance steps considered for graph generation. Number of wavelength steps Number of wavelength steps considered for graph generation. Linear scale Defines if a linear scale (Watt) or logarithmic one (dBm) is used. Minimum value If a logarithmic scale is used, this parameter defines the minimum value for the power that is displayed on the graph. Simulation Name and description Default value Unit Value range Enabled True - True, False Defines whether the component is enabled or not. 472 RAMAN AMPLIFIER—AVERAGE POWER MODEL Noise Name and description Default value Default unit Unit Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 GHz Hz, GHz, THz, nm [1,1000[ -100 dB — ]-INF,0[ 3 dB — [0,+INF[ Convert noise bins — — True, False Determines noise center frequency. Noise bandwidth Bandwidth to create noise bins. Noise bins spacing Specifies the noise bins spacing. Noise threshold Minimum value for adaptation of noise bins. Noise dynamic Threshold ratio for adaptation of noise bins. Convert noise bins Determines if generated noise bins are incorporated into the signal. Random numbers Name and description Default value Unit Value range Generate random seed True — True, False 0 — [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background In recent years, Raman amplifiers have become one of the most promising technologies for the next generation of fiber amplifiers, mostly due to their flexibility in bandwidth design. Nevertheless, the simulation techniques that are commonly used for RA's have demanded exhaustive computational time, mainly due to the use of direct integration of the coupled differential equations that describe the RA behavior [3]. The coupled differential equations have the shape observed in Equation 1. A similar set of equations, describing the backward propagation, is solved at the same time we solve the forward equations written below. 473 RAMAN AMPLIFIER—AVERAGE POWER MODEL dP f ( z, υ ) ---------------------- = α ( υ )P f ( z, υ ) + γ ( υ )Pb ( z, υ ) + dz gr ( υ – ζ ) P f ( z, υ ) ∑ --------------------- [ P ( z, ζ ) + P b ( z, ζ ) ] + K eff A eff f v<ζ gr ( υ – ζ ) –1 hΔυ ∑ --------------------- [ P f + P b ] [ 1 + exp ( [ h ( ζ – υ ) ⁄ kT ] – 1 ) ] – A eff v<ζ gr ( υ – ζ ) υ Pf ( z, υ ) ∑ --------------------- --- [ P f ( z, ζ ) + P b ( z, ζ ) ] – ζ K A eff eff v>ζ gr ( υ – ζ ) –1 2hυΔυP f ( z, υ ) ∑ --------------------- [ 1 + ( exp ( [ h ( υ – ζ ) ⁄ kT ] – 1 ) ] A eff v>ζ where Symbol υ, ζ α(υ) γ(υ) gr ( υ – ζ ) P b ( z, υ ) 474 Definition frequencies (Hz) fiber attenuation [N/m] Rayleigh back scattering coefficient [N/m] Raman gain coefficient for frequency difference ( ( υ – ζ ) ) [m/W] backward propagating power [W] A eff K eff δυ h effective core area [m2] k Boltzman’s constant polarization factor frequency interval Plank’s constant (1) RAMAN AMPLIFIER—AVERAGE POWER MODEL T temperature [K] In the equations, the following physical effects were taken into account: • pump-to-pump, signal-to-signal, and pump-to-signal Raman interactions • spontaneous Raman emission and its temperature dependency • stimulated Raman scattering • pump depletions due to Raman energy transfer • high-order Stokes generation • multiple Rayleigh back scattering • fiber loss • spontaneous emission noise A very interesting approach that considerably reduces the computational time for simulating RA is the one used for this component. The idea behind this technique is first to split the amplifier into a concatenation of small segments, and then to use the small-signal-traveling wave solution in each section (see Equation 3). In order to eliminate the z dependence in a small segment length, average powers in each section are introduced (see Equation 4). So, basically, we rearrange some terms of the original Equation 1 and reduce the propagation equations to a simpler form. This new form, suitable for the purpose of average power analyses, can be written as [2]: f ( z, v ) ⎛ dP --------------------= A ( z, v )P f ( z, v ) + B ( z, v )⎞ ⎝ dz ⎠ (2) where A ( z, v ) = – α ( υ ) + gr ( υ – ζ ) υ gr ( υ – ζ ) - [ P ( z, ζ ) + P b ( z, ζ ) ] – ∑ --- ---------------------- [ P f ( z, ζ ) + P b ( z, ζ ) ] ∑ --------------------K eff Aeff f ζ K eff Aeff v<ζ v>ζ gr( υ – ζ ) 1 – 2 hυΔυ ∑ --------------------- 1 + ----------------------------------------------------------–1 A eff exp [ h ( υ – ζ ) ⁄ kT ] – 1 v>ζ (2a) gr ( υ – ζ ) 1 B ( z, υ ) = γ ( υ )Pb ( z, υ ) + hυΔυ ∑ --------------------- [ Pf ( z, ζ ) + P b ( z, ζ ) ] 1 + ----------------------------------------------------------–1 A eff [ h ( υ – ζ ) ⁄ kT ] – 1 exp v<ζ (2b) if we substitute P f ( z, ζ ) , P b ( z, ζ ) , in (2a), (2b) in each lump by average powers in the lump, coefficients A ( z, v ) , B ( z, v ) are independent of z (within the lump, A ( υ ) , B ( υ ) and the solution of Equation 2 can be written as: ( υ )- [ exp ( ( A ( υ )H ) – 1 ) ] P f ( z 0 + H, υ ) = P f ( z 0, υ ) exp ( A ( υ )H ) + B ----------A(υ) 475 (3) RAMAN AMPLIFIER—AVERAGE POWER MODEL where H is the length of the lumps. Within each lump, powers P f ( z, ζ ) , P b ( z, ζ ) must be replaced by average powers in – 1- + B ( v )- G – 1- – 1 ⟨ P f, b ( v )⟩ = P f, b G -------------------------------1nG A ( v ) 1nG where (4) in P f, b are forward and backward propagating input powers to the lump, G = exp ( A ( υ )H ) . The user is responsible to guarantee that the term A ( v ) does not become zero. For example, it is impossible to simulate the chromatic dispersion of just one signal if the attenuation is not considered, once the term A ( v ) will become zero. Numerical approach The relaxation method is used in order to satisfy the boundary conditions of the twopoint boundary problem with given accuracy. There are two different iteration procedures, for both forward and backward directions. Forward direction is from Input port 1 to Output port 1, and backward is from Input port 2 to Output port 2. The first procedure, the innermost one, is intended to evaluate the self-consistent convergence for the average powers used in Equation 4 for every amplified segment. When a certain tolerance is reached (10-12), the average powers are considered good enough to be used as an approximation of the desired functions. In the outermost one, or second procedure, the convergence is checked after the integration in forward direction is performed. If the variance in the gain is less than the tolerance desired (see “Numerical” on page 471), the simulation is considered finished. Otherwise, the component runs for the maximum number of iterations set by the user. The reason for the reduction in computational time is that direct numerical integration of Equation 1 is replaced by algebraic operations. The user can choose the signals that will be used in the convergence checking. There are two available choices: All signals and First signal. When the First signal option is chosen, just the signal with the smallest wavelength is used in checking the convergence by the given tolerance. Otherwise, if the All signals option is chosen, all signals are used in the checking. In the case where there a signal has not been transmitted, the convergence test is performed based on the pumps. 476 RAMAN AMPLIFIER—AVERAGE POWER MODEL Files Some data necessary for this model may be downloaded from a file. In general, these files are in the ASCII format and follow Optiwave's standard format. For clarity, the units of each column in the files are listed in the following table. Field First column Second column Attenuation Wavelength (nm) Attenuation (dB/km) Effective area Wavelength (nm) Effective area (µm2) Raman gain X frequency Frequency shift (THz) Normalized Raman gain 2 m -----W Raman gain efficiency X frequency Frequency shift (THz) Rayleigh back scattering Wavelength (nm) Raman gain efficiency 1 ------------W⋅m Back scattering (1/km) When a file with the normalized Raman gain is used, it must be provided values for the Raman gain peak and Raman gain reference pump to use in the calculation of the Raman gain used in the simulation. The following formula is used: P g R = -----R- g N λp where g R is the Raman gain, P R is the Raman gain peak, pump and g N is the normalized Raman Gain. The unit of Raman gain is given in λ p is the gain reference m ----- . W Comparison As stressed in the beginning of the technical description, the average power model is intended to decrease the computational time required to solve the Raman Amplifier differential equations by simplifying the way the equations are written. In fact, the model shows a reduction in computation time of over two orders of magnitude [2] compared to the model using direct integration approach (fourth-order Runge-Kutta). However, in some cases, it is known that the model fails in converging (for example, when the total pump becomes very high). Therefore, based on the characteristics presented, this model is very useful in getting a first approximation for a network under certain limits. Once the rough estimation is reached, the system could be generalized using the full steady state model. A validation example for this model is presented in Lesson: "Raman amplifier Average power model" in the tutorials section. 477 RAMAN AMPLIFIER—AVERAGE POWER MODEL References: [1] M. Karasek, M. Menif, "Protection of surviving channels in pump-controlled gain-locked Raman fibre amplifier", Optics Communications 210 (2002) 57-65. [2] B. Min, W. J. Lee, N. Park, "Efficient Formulation of Raman Amplifier Propagation Equations with Average Power Analysis", IEEE Photonics Technology Letters, Vol. 12, No. 11, November 2000. [3] E. Desurvire, "Erbium-doped fiber amplifiers: principles and applications", Wiley-Interscience, 1994. [4] S. Tariq, J.C. Palais, "A Computer Model of Non-Dispersion-Limited Stimulated Raman Scattering in Optical Fiber Multiple-Channel Communications", IEEE Journal of Lightwave Technology, Vol. 11, No. 12, December 1993. 478 RAMAN AMPLIFIER—DYNAMIC MODEL Raman Amplifier—Dynamic Model This component simulates a Raman amplifier using a dynamic model based on direct integration of the differential equations that describe it. Ports Name and description Port type Signal type Input 1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical Parameters Main Name and description Symbo l Default value Default unit Value range Length L 10 km ]0; 1,000,000[ — Constant — Constant, From file α 0.2 dB/km [0,+INF[ — FiberLoss.dat nm - dB/km — Amplifier length. Attenuation data type Defines if attenuation is entered as scalar, used for all wavelengths, or if it is wavelength dependent / downloaded from a file. Attenuation Constant attenuation value Attenuation file Attenuation value dependent on wavelength. 479 RAMAN AMPLIFIER—DYNAMIC MODEL Name and description Symbo l Default value Default unit Value range Effective area data type — Constant — Constant, From file A eff 72 µm2 ]0, +INF[ — EffectiveArea.dat nm - µm2 — — Raman gain — Raman gain, Raman gain efficiency — 1e-013 — [0,+INF[ — 1000 nm [0,+INF[ gr RG.dat THZ normalized Raman gain — Name and description Symbo l Default value Default unit Value range Temperature T 300 K [0,500] Defines if effective area is entered as scalar, used for all wavelengths, or if it wavelength dependent/downloaded from a file. Effective interaction area Constant effective area. Effective interaction area file Effective area dependent on wavelength. Raman gain type Defines type of Raman gain. If Raman gain efficiency is selected, effective area is disabled, and value is g r / Aeff . Otherwise, is normalized g r multiplied by Raman gain peak (see below). Raman gain peak Normalized Raman gain is multiplied by Raman gain peak. Formula is detailed later in this section. Raman gain reference pump Value used for Raman gain calculation. Formula is detailed later in this section. Gain X frequency File that defines Raman gain or the Raman gain efficiency. Enhanced Absolute temperature at which fiber is operating. Used for noise consideration. 480 RAMAN AMPLIFIER—DYNAMIC MODEL Name and description Symbo l Default value Default unit Value range Polarization factor K eff 2 — [1,2] — Constant — Constant, From file γ- 5.0e-005 1/km [0, +INF[ — Rayleigh.dat nm - 1/km — — 1450 nm [0,3000] — False — True, False — 16.75 ps/nm/km ]-INF, +INF[ — 0.075 ps/nm2/km -INF, +INF[ — 1550 nm [100, 2000] Actual value depends on relative polarization of fields of channels i and j. Equals 1 if fields of both channels are polarization-aligned, and 2 for totally scrambled polarization [4]. Rayleigh back scattering data type Defines whether Rayleigh back scattering coefficient is entered as scalar, used for all wavelengths, or wavelength dependent/downloaded from a file. Rayleigh back scattering Constant Rayleigh back scattering. Rayleigh back scattering file Rayleigh back scattering dependent on wavelength. Upper pump reference Used for convergence test. All wavelengths below this value are considered pump, and are not taken into account for the convergence test. Enable dispersion Enables the linear chromatic dispersion application for the signals. Dispersion The value of the GVD (Group Velocity Dispersion) parameter in the wavelength domain. Dispersion slope The value of the dispersion slope parameter. Reference wavelength This value is used internally as a “zero” or reference frequency in the spectrum of the signal envelope. The attenuation value is assumed to correspond to this frequency. 481 RAMAN AMPLIFIER—DYNAMIC MODEL Name and description Symbo l Default value Default unit Value range Group delay data type — Constant — Constant, From file 1/Vg(v) 4900000 ps/km [0, 1010] — GroupDelay.dat ns—ps/km — Defines if the group delay is entered as a scalar used for all wavelengths, or if it wavelength dependent/entered from a file. Group delay Constant group delay Group delay file Numerical Name and description Default value Unit Value range Tolerance 0.01 — ]0,+INF[ 50 — [1;50,000] 50 — [1;50,000] All signals - All signals, First signal Used to check convergence of the model. Based on gain of the signals. Number of divisions Number of divisions (in space) of the fiber. Number of iterations Maximum number of iterations to be executed. If convergence is not reached in this number of iterations, model returns the calculated values regardless. Check convergence using: Defines if convergence is checked using “All signals” or “First signal”. Reference time Determines the instant of time used to take the powers to use as input powers in the fiber to solve the steady-state regime that will determine the initial values. Graphs Name and description Default value Unit Value range Calculate graphs False - True, False Defines if graphs are calculated or not. If False, component graphs are not represented. 482 RAMAN AMPLIFIER—DYNAMIC MODEL Name and description Default value Unit Value range Number of distance steps 20 - [1,1e8] 20 - [1,1e8] True - True, False -50 dBm ]-INF,+INF[ Number of distance steps considered for graph generation. Number of wavelength steps Number of wavelength steps considered for graph generation. Linear scale Defines if a linear scale (Watt) or logarithmic one (dBm) is used. Minimum value If a logarithmic scale is used, this parameter defines the minimum value for the power that is displayed on the graph. Simulation Name and description Default value Unit Value range Enabled True - True, False Defines whether the component is enabled or not. Noise Name and description Default value Default unit Unit Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 GHz Hz, GHz, THz, nm [1,1000[ -100 dB — ]-INF,0[ 3 dB — [0,+INF[ Convert noise bins — — True, False Determines noise center frequency. Noise bandwidth Bandwidth to create noise bins. Noise bins spacing Specifies the noise bins spacing. Noise threshold Minimum value for adaptation of noise bins. Noise dynamic Threshold ratio for adaptation of noise bins. Convert noise bins Determines if generated noise bins are incorporated into the signal. 483 RAMAN AMPLIFIER—DYNAMIC MODEL Random numbers Name and description Default value Unit Value range Generate random seed True — True, False 0 — [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background It is widely believed that Raman Amplifier (RA) will play an increasing role in future optical fiber communication (OFC) systems [1]. They have already been widely utilized due to their fundamental advantages [1]: • there is amplification at any wavelength, provided the appropriate pump sources are available. • a fiber itself can be used as an active medium. • a pump spectrum determines a gain spectrum. The equations that describe a Raman amplifier are [2]: ± ± − ± ∂P ( z, t, υ -) − 1 ∂P ( z, t, υ ) + ---------------------------+ -------------- ----------------------------- = − + α ( υ )P ( z, t, υ ) ± γ ( υ )P ( z, t, υ ) ± ∂z Vg ( υ ) ∂t gr ( υ – ζ ) ± − ± P ( z, t, υ ) ∑ --------------------- [ P ( z, t , ζ ) + P + ( z, t , ζ ) ] ± K eff Aeff v<ζ gr ( υ – ζ ) ± − –1 hΔυ ∑ --------------------- [ P ( z, t, ζ ) + P + ( z, t, ζ ) ] [ 1 + ( exp [ h ( ζ – υ ) ⁄ kT ] – 1 ) ] − + Aeff v<ζ gr ( υ – ζ ) υ ± − ± P ( z, t, ζ ) ∑ --------------------- --- [ P ( z, t, ζ ) + P + ( z, t, ζ ) ] − + K eff A eff ζ v>ζ gr ( υ – ζ ) ± –1 2hυΔυP ( z, t, ζ ) ∑ --------------------- [ 1 + ( exp ( [ h ( υ – ζ ) ⁄ kT ] – 1 ) ] A eff v>ζ 484 (1) RAMAN AMPLIFIER—DYNAMIC MODEL where Symbol Definition υ, ζ frequencies (Hz) Vg ( υ ) α(υ) γ(υ) gr ( υ – ζ ) P b ( z, υ ) A eff K eff δυ h k T frequency-dependent group velocity fiber attenuation [N/m] Rayleigh back scattering coefficient [N/m] Raman gain coefficient for frequency difference ( ( υ – ζ ) ) [m/W] backward propagating power [W] effective core area [m2] polarization factor frequency interval Plank’s constant Boltzman’s constant temperature [K] In these equations, the following physical effects were taken into account: • pump-to-pump, signal-to-signal and pump-to-signal Raman interactions; • spontaneous Raman emission and its temperature dependency; • stimulated Raman scattering; • pump depletions due to Raman energy transfer; • high-order stokes generation; • multiple Rayleigh backscattering; • fiber loss; • spontaneous emission noise. In this component, the equations in Equation 1 (forward and backward) are solved spatially through direct integration using a standard classical fourth-order RungeKutta formula without adaptive step size [3]. Numerical approach The convergence of the model is checked in two directions: forward and backward. An iterative forward and backward integration of propagation equations must be applied because backward propagating ASE powers and a counter-directional pumping scheme may be defined, and the possibility of counter directional signal 485 RAMAN AMPLIFIER—DYNAMIC MODEL propagation [2]. The forward direction is from Input Port 1 to Output Port 1 and backward is from Input Port 2 to Output Port 2. The iterative scheme is started with a forward integration of forward signals, propagating ASE spectral components, and pumps. The backward pumps and backward ASE powers are set to zero. At each backward integration, the final results + P ( z = L, υ ) of the previous forward integration, together with the boundary conditions for the backward pump, backward ASE powers, and backward signals, are used as starting conditions. Similarly, the results of the previous backward integration P _ ( z = 0, υ ) together with the boundary conditions for forward signal channels, pumps, and forward ASE, are used as starting conditions for each forward integration [2]. The convergence checking is done after integration in the forward direction is complete. If the variance in the gain is less than the tolerance desired (see “Numerical” on page 482) , the simulation is considered complete. Otherwise, the component runs for the maximum number of iterations set by the user. The user can choose the signals that will be used in the convergence checking. There are two available choices: All signals and First signal. When the First signal option is chosen, just the signal with the smallest wavelength is used in checking the convergence by the given tolerance. Otherwise, if the All signals option is chosen, all signals are used in the checking. In the case where there a signal has not been transmitted, the convergence test is performed based on the pumps. After the spatial integration is complete, the time evolution of pumps, signals, and amplified spontaneous emission waves is performed by direct integration with Equation 1, starting with the steady-state solution for longitudinal distribution of individual powers along the Raman fiber. To avoid possible oscillations of the solution in time domain, care must be taken in the selection of bin widths used in space ( Δz ), and time ( Δt ) discretization schemes. Stable solutions has been obtained when the time bin ( Δt ) is equal to or less than the propagation time through a space bin Δt ≤ Δz ⁄ V g . In order to determine the rise/fall times of the surviving channel power transients with sufficient resolution, the ratio of time and space bins –9 Δt ⁄ Δz = 4 × 10 [ s ⁄ m ] should be independently kept for the Raman fiber length, as in the examples. Some data necessary for this model may be downloaded from a file. In general, these files are in the ASCII format and follow Optiwave's standard format. 486 RAMAN AMPLIFIER—DYNAMIC MODEL For clarity, the units of each column in the files are listed in the following table. Field First column Second column Attenuation Wavelength (nm) Attenuation (dB/km) Effective area Wavelength (nm) Effective area (µm2) Raman gain X frequency Frequency shift (THz) Normalized Raman gain 2 m -----W Raman gain efficiency X frequency Frequency shift (THz) Rayleigh back scattering Wavelength (nm) Raman gain efficiency 1 ------------W⋅m Back scattering (1/km) When a file with the normalized Raman gain is used, it must be provided values for the Raman gain peak and Raman gain reference pump to use in the calculation of the Raman gain used in the simulation. The following formula is used. P g R = -----R- g N λp g R is the Raman gain, P R is the Raman gain peak, λ p is the gain reference pump and g N is the normalized Raman Gain. where The unit of Raman gain is given in m- . ---W 487 RAMAN AMPLIFIER—DYNAMIC MODEL References: [1] E. M. Dianov, "Advances in Raman Fibers", Journal of Lightwave Technology, Vol. 20, No. 8, August 2002. [2] M. Karasek, M. Menif, "Protection of surviving channels in pump-controlled gain-locked Raman fibre amplifier", Optics Communications 210 (2002) 57-65. [3] W. H. Press, et al., "Numerical Recipes: The Art of Scientific Computing", 2nd Edition, Cambridge University Press, 1992. [4] S. Tariq, J.C. Palais, "A Computer Model of Non-Dispersion-Limited Stimulated Raman Scattering in Optical Fiber Multiple-Channel Communications", IEEE Journal of Lightwave Technology, Vol. 11, No. 12, December 1993. 488 EDFA BLACK BOX EDFA Black Box Designs erbium doped fiber amplifiers (EDFAs) pumped by 980 nm or 1480 nm. Requires just the experimental characterization of a practical device such as the gain spectrum and noise figure under nonsaturated and saturated conditions. Details about erbium-doped fiber specifications and elements in the layout are not required to perform the simulations. The amplifier is specified to operate under conditions required by wavelength division multiplex (WDM) systems. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Operation mode Saturation — — Gain control, Power control, Saturation 20 dB — [0,100] 5 dBm W, mW, dBm [-100,100] Amplifier operation mode Gain Determines the signal gain Power Determines the signal output power 489 EDFA BLACK BOX Measurements Name and description Default value Units Value range File wavelength unit m — nm, m, Hz, THz Gain1.dat — — Gain2.dat — — 0.1 nm [0.0001,10] Power dBm Power, Spectral density, Noise figure True — True, False Noise.dat — — 1540 nm [800,1700] Saturation.dat — — Name and description Default value Units Value range Relative error 0.1 dB ]0,100] Cubic — Linear, Cubic Determines the wavelength unit First gain spectrum file name Filename with the gain spectra measurements Second gain spectrum file name Filename with the gain spectra measurements OSA bandwidth Set the bandwidth of the Optical Spectrum Analyzer Noise type Select the noise type Noise Determines if ASE is included in the calculation or not Noise spectrum file name Filename concerning the noise spectra Saturation wavelength Determines the saturation wavelength Saturation file name Filename concerning the saturation spectra Numerical Determines the relative error acceptable in each calculation Interpolation algorithm Determines the interpolation algorithm for the measured data 490 EDFA BLACK BOX Polarization Name and description Default value Units Value range Polarization filter None — None, Polarization X, Polarization Y Name and description Default value Units Value range Enabled True — True, False Determines the polarization of the filter Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise bins spacing 125 GHz Hz, GHz, THz, nm [1,1000] –100 dB — ]-INF,0[ 3 dB — [0,+INF] Convert noise bins — — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 491 EDFA BLACK BOX Graphs Name and description X Title Y Title First gain spectrum Wavelength (m) Gain (dB) Second gain spectrum Wavelength (m) Gain (dB) Noise spectrum Wavelength (m) Power (dBm) Saturation Input power (dBm) Gain (dB) Technical background Using input parameters as the characterization of the gain spectrum and noise figure under non-saturated and saturated conditions measured to a practical device is sufficient for designing the amplifier performance using this black box model. Additional information concerning fiber specifications, such as absorption and emission cross-sections, erbium doping, core radius, or details related to the amplifier layout, is not required in this case. Curves containing the amplifier characterization are available internally as a default in the software, which makes it possible for you to perform simulations. Three different control modes are available that allow you to perform the amplifier analysis under distinct points of view. Each mode control – gain, power control, and saturation – defines a different amplifier operating condition. The black box model enables passive components, such as optical isolators, equalizer filters, and several types of couplers, to be included in the amplifier design while considering an additional loss variation along the amplifier due to the active and passive components. The gain and the noise characterization measured to distinct states of operation are provided as input files that enable the complete modelling of the amplifier performance. Operation Modes Fiber amplifiers used in WDM systems usually make use of control systems as power or gain. It is useful to include the option in the EDFA Black Box to select one of three operation modes: 492 • Gain mode: Based on a control of the amplifier gain (Gain Control) relating the input and output signals (with or without the generated amplified spontaneous emission (ASE). • Power Control mode: Considers the value of the output power to control the amplifier performance (Power Control). • Saturation mode: Considers the amplifier operating in a saturated condition (Saturation). EDFA BLACK BOX Gain Control mode In this mode, you set the gain amplifier (Gain in dB units). The gain calculation is performed using Equation 1, where the total input (Pin) and the output (Pout) power spectra are considered. The specified amplifier gain (Gspeci) is given by the ratio of the total output power and input total power, with or without the generated ASE. +∞ ∑ Pout ( λ ) + ∫ λ S ASE ( f ) df (1) –∞ G speci = -------------------------------------------------------------P ( λ ) ∑ in λ SASE(f) represents the spectral density of the amplified spontaneous emission integrated on the optical frequency f. Note: You can include the noise by selecting the noise type as power, spectral density, or noise figure in the EDFA Black Box Properties dialog box. Power Control mode The value that you define in the power control mode is the desired amplifier output power (Power in dBm units). The specified amplifier output power (Pspeci) that includes the spectral ASE is: Pspeci = G × ∑ P in ( λ ) – λ where +∞ ∫ S ASE ( f ) df (2) –∞ G is the amplifier gain. The option to select the noise type that will be included in the simulations is also available in this control mode. Saturation mode In the saturation mode, the gain is the specified parameter. The noise type can be selected in this mode, and two experimental gain curves are inserted as input files considering two different saturation conditions. The gain curve in a saturated condition is provided in a file format containing two columns. The first column refers to the signal output power given in [dBm] units. The second column gives the gain in [dB] units. 493 EDFA BLACK BOX An example of the saturated gain input file is: Signal output power (dBm) Gain (dB) –40 28.82 –30 28.83 –20 28.82 –10 28.81 0 28.72 ... where the signal output power is given in [dBm] units and the gain is in [dB] units. There is no limit of rows or power spacing previously defined. Basic equations The black box model considers a two-level Er3+ system assumption that is usually adopted to model erbium-doped fiber amplifiers [1]. The propagating equation written as a function of the absorption and emission coefficients, α(λ) and γ(λ) respectively, is [2]: dP ( λ ,z -) = { [ α ( λ ) + γ ( λ ) ]I ( z ) – α ( λ ) }P ( λ ,z ) + γI ( z )P eq ( λ ) -----------------ASE dz (3) I(z) represents the fraction of active ions in the excited state, P(λ,z) describes the propagating power at a specific wavelength and fiber position, and PASEeq is the term that includes the amplified spontaneous emission (ASE) as an equivalent ASE power. The solution to Equation 3 is: eq P ( λ ,L ) = G ( λ ) [ P ( λ ,0 ) + P ASE ( λ ) ] (4) where L is the total Er-doped fiber length and P(λ,0) represents the power at the wavelength λ and at the fiber input. Considering the scope of this approximation, PASEeq(λ) works as an independent source of amplified spontaneous emission. The total gain along the erbium-doped fiber is: G z ( λ ) = exp { { α ( λ ) + γ ( λ ) }I z – α ( λ ) × z } (5) where I z is the updated term that represents the detailed evolution of the population inversion along the erbium-doped fiber. The black box model takes into account a multiple-stage amplifier, where all amplifier stages use the same type of erbium-doped fiber (the same absorption and emission 494 EDFA BLACK BOX coefficients are considered). Figure 1 shows a sketch of an amplifier set up in two sections, containing passive elements such as optical isolators, couplers, taps and one filter. The total Er-doped fiber length and the total gain are L and G ( λ ) respectively. Figure 1 Erbium doped amplifier set up in multiple stages, where the black box parameters G ( λ ) , IL ( λ ) , ILin ( λ ) are indicated If the insertion loss is included in the analysis, the gain G ( λ ) is written as: G ( λ ) = [GA ( λ ) + GB ( λ ) ]/ IL ( λ ) . Amplifier gain In order to model the gain of the amplifier, two different states of operation are considered where each state has a characteristic population inversion. The amplifier gain expression is given as a function of a reference gain value, (for example, [2]): log G ( λ ) = T λref ( λ ) [ log G ( λ ref ) – log G ref ( λ ref ) ] + log G ref (λ) (6) ref where λ ref and G ( λ ref ) specifies the wavelength and the gain at a reference amplifier operating point. The term Tλref ( λ ) is named tilt function and is obtained by the ratio of the gain curves measured in the two states of operation. One acts as a reference curve (for example, ref G ( λ ) ). The tilt function is given by the analytical expression: log G 1 ( λ ) – log G 2 ( λ ) T ( λ ) = --------------------------------------------------------------log G 1 ( λ ref ) – log G 2 ( λ ref ) (7) 495 EDFA BLACK BOX where G 1 ( λ ) and G 2 ( λ ) are the gain measured to the state1 and state2 respectively of the amplifier operation. The experimental gain, measured at these two states of operation, is provided as input file in the black box model. It is convenient to introduce this concept of tilt function in the model, since it considers the interdependence between the ratio of the characteristic gain and the absorption and emission coefficients. On the other side, as the internal losses IL(λ) caused by passive elements modify both G1(λ) and G2(λ) in the same manner, the tilt function isn’t affected by optical circuitry variations. By choosing G2(λ) equal to G(λ), the expression for the amplifier at the operation point is: log G ( λ ) = log G 1 ( λ ) – T λref ( λ ) × [ log G 1 ( λ ref ) – log G ref ( λ ref ) ] log G ( λ ) = log G 2 ( λ ) + T λref ( λ ) × log ΔG (8) (9) ref where log Δ G specifies the gain difference between log G ( λ ref ) – log G 2 ( λ ref ) or log G 1 ( λ ref ) – log G 2 ( λ ref ) . The term log Δ G is a free parameter and may be altered to adjust the gain. Gain measurement The gain curves are critical to the black box model operation. The best way to obtain these values used as input files in the model is by measuring them in a practical amplifier. It is important to note that the precision of these measurements defines the accuracy of the simulated results. However, the model alternatively accepts curves generated by a simulated amplifier that supplies gain and ASE curves as the output files. Obtaining Gain Curve G1 The first gain profile is acquired with the amplifier operating in a constant saturated regime that assures a specific population inversion. This condition can be obtained by coupling a large signal input power to the amplifier, typically −10 dBm, at the wavelength λref (e.g., 1540 nm), which is maintained constantly. A small signal with power equal to −30 dBm (for instance) is added to the amplifier input as a probe signal. Its frequency (probe signal) is scanned through the range defined by the two-limit frequencies, which is written in terms of signal wavelength and usually varies from 1530 nm to 1570 nm. This scan over the probe signal allows you to obtain the spectral gain for one specific saturated condition. This method was checked by analyzing a series of gain curves measured at the same saturated conditions, and a nominally identical population inversion was recorded [2]. 496 EDFA BLACK BOX Obtaining Gain Curve G2 Analogous measurement procedure is repeated to obtain the second gain profile. However, in this case, the probe signal input is enlarged to –20 dBm, and the reference signal at a selected wavelength (1540 nm) can be varied. This new signal input combination results in a different population inversion condition, which characterizes the gain G 2 ( λ ) . The difference is that the added signal test presents larger potency, typically −20 dBm, which causes a change in the gain curve profile by saturating the amplifier. With the value obtained for the gain in each wavelength, the gain curve profile is obtained. The high signal power, with the same λref, can also be altered, since the total sum of the power is larger than the sum of the power to generate the curve G1. The experimental gain curves must be provided in files containing two columns. The first column refers to the wavelength specified in [nm], [m], [Hz] or [THz] units. The second column gives the gain in [dB] units. As an example of the gain input file is: Wavelength [nm] G [dB] 1535.58 38.17 1538.95 34.09 1542.11 33.35 1545.26 33.17 ... where the wavelength is given in [nm] units and the gain is in [dB] units. There is no limit of rows or wavelength spacing previously defined. Amplifier noise figure The noise figure is the figure of merit that usually describes the amplifier noise performance. In order to evaluate the noise figure, three different options are available. You can select the input format of noise that will be considered to perform the calculations. The first option is to select the noise input in terms of ASE power. In this case, the ASE noise spectral density is written as: ( λ )S power ( λ ) = P ----------Δf (10) where P(λ) is the ASE power measured at each wavelength range and Δf is the bandwidth considered in the ASE spectrum acquisition. 497 EDFA BLACK BOX Another option to evaluate the amplifier noise performance is to select the ASE spectral density. In this case, the spectral density S(λ) is required as input file and is written as: S ( λ ) = hf [ 10 NF ( λ ) ⁄ 10 × G(λ ) – 1] (11) where h is the Planck constant, f is the optical frequency, and the exponent NF(λ) is the noise figure as a function of the signal wavelength. The model will internally calculate the noise figure considering the noise curve provided as input file. Rewriting Equation 11 in terms of noise figure produces [3]: S ( λ ) + hfNF ( λ ) = 10 log ----------------------hf × G ( λ ) (12) The third option is to select the noise figure value given as a function of the signal wavelength. In this case, the ASE spectrum is modeled considering the provided noise figure value. It is also possible to evaluate the noise figure considering different amplifier state operation that means to consider distinct gain values. In this case, the spectral density given by Equation 11 is rewritten including the gain variation (ΔG in linear units or logΔG in dB units). The new spectral noise density is dependent on the amplifier gain and is: S ( λ ,log ΔG ) = hf 10 NF ( λ ) ⁄ 10 × G ( λ ,log ΔG ) – 1 (13) where log Δ G can be calculated from Equation 8 and Equation 9. Equivalent ASE noise measurement The experimental ASE noise curves complement the measured parameters required by the black box model. Obtaining equivalent ASE noise The third input to obtain (experimental) is the amplified spontaneous emission. In the ASE acquisition curve, only the saturating signal must be maintained turned-on and operating with a constant power at a specified signal wavelength (1540 nm as suggested in the previous measurement descriptions). This is sufficient to produce population inversion along the Er-doped fiber. The spectrum obtained at the fiber output registers the amplified spontaneous emission observed along the whole wavelength range considered (1530 nm to 1570 nm, typically). 498 EDFA BLACK BOX The experimental gain curves must be provided in files containing two columns. The first column refers to the wavelength specified in [nm], [m], [Hz] or [THz] units. The second column gives the ASE noise curve in [dBm] units. An example of input file: Wavelength [nm] ASE [dBm] 1543 –25.13 1544 –25.20 1546 –25.42 1551 –26.43 where the wavelength is in [nm] units and the gain is in [dB] units. There is no limit of rows or wavelength spacing previously defined. 499 EDFA BLACK BOX References [1] E. Desurvire, “Erbium-Doped Fiber Amplifiers – Principles and Applications”, John Wiley & Sons, Inc., USA, 1994. [2] J. Burgmeier, A. Cords, R. März, C. Schäffer, B. Stummer “A black box model of EDFA’s operating in WDM systems”, J. Lightwave Technol., Vol. 16, N. 7, pp. 1271-1275, 1998. [3] S. P. Bastien, H. R. D. Sunak, B. Sridhar, V. E. Kalomiris “Temporal, spatial and spectral modeling of erbium doped fiber amplifiers”, SPIE – Physic and Simulations of Optoelectronic Devices, pp. 2-11, 1992. 500 EDF DYNAMIC-FULL MODEL EDF Dynamic-Full Model Incorporates time-varying input signal and pump powers that enable simulating dynamic effects presented by erbium-doped amplifiers inserted in a fiber link. This powerful tool solves the full rate and propagation equations in the time and spatial domain. The powers and population densities are calculated as a function of the time variation at each point of the z fiber. This model is specifically designed to simulate cascaded amplifiers in a long fiber link, considering multiple signal input. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 5 m — [0, 1e4] 10 ms — ]0, +INF[ 0.01 dB/m — [0,100] 0.015 dB/m — [0,100] Fiber specification — — Fiber specification, Saturation parameter Specifies the doped fiber length Er metastable lifetime Specifies the Erbium metastable lifetime Loss at 1550 nm Determines the fiber loss at 1550 nm Loss at 980 nm Determines the fiber loss at 980 nm Input data Determines if saturation parameter is used or not 501 EDF DYNAMIC-FULL MODEL Name and description Default value Default unit Units Value range Saturation parameter 4.4e+015 1/(s.m) — [1e-10, +INF[ 0.24 — — [0.1,1] 1e+025 m–3 m–3~ppm-wt ~wt% [1,+INF[ 2.2 μm — [0,1, 10] 2.2 μm — [0.1, 10] Name and description Default value Units Value range OptiAmplifier format False — True, False nm — nm, m, Hz, THz Erbium.dat — — Name and description Default value Units Value range Relative error 0.0001 — ]0,1] 100 — [10,10000] 100 — [10,10000] Specifies value of saturation parameter Numerical aperture Specifies the numerical aperture of the Er-doped fiber Er ion density Specifies the Er doping in the Er-doped fiber Core radius Specifies the fiber core radius Er doping radius Species the Erbium doped radius Cross-sections Determines the format of the OptiAmplifier file File frequency unit Determines the frequency unit of the file with the measurements cross-section file name Determines the cross-section file Numerical Determines the relative error acceptable in each calculation for the steady-state solution used as initial condition for the dynamic behavior Max. number of iterations Specifies the maximum number of times to repeat the longitudinal integrations for the powers when solving the steady-state equations used as initial condition for the dynamic behavior Longitudinal steps Determines the number of longitudinal steps in the calculation 502 EDF DYNAMIC-FULL MODEL Name and description Default value Units Overlap factor data Calculate Calculate, Load from file LP01 Marcuse Gaussian, Whitley Gaussian, Desurvire Gaussian, Myslinski Gaussian, LP01 Determines whether the overlap factor values will be calculated by the component or it will be loaded from a file Geometrical model Determines whether the component will calculate the overlap factor using one of the gaussian approximations, or the LP01 mode Overlap factor file name Value range OverlapFactor. dat Specifies the overlap factor file name Reference time 0.5 / ( Bit rate ) s [0,1e10] Name and description Default value Units Value range Enabled True — True, False Determines the instant of time used to take the powers to use as input powers in the fiber to solve the steady-state regime that will determine the initial values Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30,30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 GHz Hz, GHz, THz, nm [1,1000] –100 dB — ]-INF,0[ 3 dB — [0,+INF[ Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins spacing Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 503 EDF DYNAMIC-FULL MODEL Name and description Default value Default unit Units Value range Convert noise bins Convert noise bins — — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description X Title Y Title Absorption parameters Wavelength (m) Cross-section (m2) Emission parameters Wavelength (m) Cross-section (m2) Average population density N2 Time (s) N2 504 EDF DYNAMIC-FULL MODEL Technical background Different solutions to the problem of transient fluctuations due to gain cross-saturation observed in EDFAs inserted in multi-wavelength networks have been suggested. Gain cross-saturation in fiber amplifiers induces transients in the surviving channels remaining as a consequence of the process of adding or removing channels in the network reconfiguration. Although this perturbation will be small in a single amplifier, it becomes considerable along cascaded amplifiers. As a result, a tool that enables analyzing the effects of addition and/or dropping wavelength channels in a multiwavelength optical network containing EDFAs is important. In opposition to the steady-state model (EDF module), the EDF Dynamic enables you to calculate the variation of signals and pumps power with the time when sampled channels are present in the layout. The dynamic behavior of cascaded EDFAs can be simulated as well. The results will help you design cascaded amplifier systems with suppression of both transient and steady state signal power fluctuations due to channel addition/removal. The numerical EDF Dynamic uses a two-level system approximation and is based on the solution of the propagation and rate equations for transitions between the upper and lower levels. These equations are given by Equation 1, Equation 2, and Equation 3, which are also in the technical background for the Erbium Doped Fiber [1]: ∂N 2 ( z ,t ) N 2 ( z ,t ) 1 N e a a + – -------------------- = – ----------------- – ------- ∑ { Γ n [ ( σ n + σ n )N 2 ( z ,t ) – σ n ] } [ P n ( z ,t ) + P n ( z ,t ) ] ∂t τ A eff n = 1 (1) N2 + N1 = 1 (2) ± ∂P n ( z ,t ) e a a ± e ---------------------- = u n { ρΓ n [ ( σ n + σ n )N 2 ( z ,t ) – σ n – α ] }Pn ( z ,t ) + 2ρΔνN 2 Γ n σ n ∂z (3) where the optical powers are expressed in units of number of photons per unit time, τ is the metastable spontaneous emission lifetime, N is the number of channels taken into account in the simulation (including signals, pumps, and ASE bins), ρ is the number density of the active erbium ions, α is the attenuation coefficient (which takes into account the background loss of the fiber), Δν is the frequency step used in the simulation to resolve the ASE spectrum, and Aeff is the effective doped area given 505 EDF DYNAMIC-FULL MODEL 2 by π × b , where b is the Er doping radius (it is considered a uniform distribution of erbium ions in the area given by the Er doping radius region). The nth channel of wavelength λ n has optical power Pn(z,t) at location z and time t, e a with emission and absorption cross-section σ n and σ n respectively, and confinement factor Γ n . The superscript symbols + and – are used to indicate channels traveling in forward (from 0 to L) and backward (from L to 0) directions, respectively. For beams traveling in the forward direction u n = 1 and for beams in the opposite direction u n = – 1 . The overlap integrals Γ n between the LP01 mode intensity (which is used in this program) distribution doped region area are given by: b ∫ E ( r ,ν ) 2 ∫ E ( r ,ν ) 2 r dr 0 Γ n ( ν ) = --------------------------------∞ r dr 0 (4) where E(r, ν ) gives the electric field intensity. This model assumes that the signal and pump powers change slowly compared to the optical transit time in the fiber. This assumption is valid since the typical time that the light takes to pass by one 100 m fiber (one EDFA does not use fibers larger than that) is 500 ns. The time scales we deal with are always on the order of microseconds or longer. Numerical solution The solution of the time-dependent rate equations and the propagation equations is based on the assumption that the atomic populations remain constant during a time step δt , typically microseconds. This assumption is acceptable since the metastable lifetime is relatively long (around 10 ms) and the transit time of photons through the Er3+-doped fiber is short. Initial values for the population of the upper level in each point of the fiber of the program first solves the steady-state case. The parameter reference time determines the instant of time used to take the powers that will be used as input powers in the fiber to solve the steady-state regime that will determine the initial values for the population levels. When the calculation of the dynamic behavior for the sampled signal and pump channels starts at t=0, the program assumes that the population inversion is already different from zero, and the value of the population of the upper level at each point of the fiber (N2(z)) is given as t=0 by the powers at the reference time. Generally speaking, you will be interested in the behavior of the amplifier in scales of times that go from a few microseconds to some tens of milliseconds. It is important to set the bit rate and the sequence length of the simulations in such a way that the time windows obey this requirement. If the time windows in your simulation are too short (for example, by a few nanoseconds), the gain of the EDF Dynamic amplifier will be 506 EDF DYNAMIC-FULL MODEL given at almost all instants by the gain that one amplifier operating in the steady-state regime with the input powers given by the reference time would have, because the time response scales in EDFA are always on the order of microseconds or longer. The parameterized channels and noise bins input powers are considered constant in time. The output powers for these channels are average in time. This means that during the calculation, the program saves the output powers that each one of these channels would have at each sample point, and then gives as output power the sum of the power at each sample divided by the total number of samples. References [1] C.R. Giles and E. Desurvire, “Modeling erbium-doped fiber amplifiers,” Journal of Lightwave Technology, Vol. 9, N. 2, pp. 271-283, 1991. 507 EDF DYNAMIC-FULL MODEL Notes: 508 EDF DYNAMIC—ANALYTICAL MODEL EDF Dynamic—Analytical Model Enables you to simulate the dynamic response of an EDF for input powers that vary in time. In opposition to the EDF Dynamic-Full Model component, it doesn't solve the full rate and propagation equation. Neglecting ASE these equations can be solved analytically, which is described in this module. An additional approximation which considers the population of the upper level constant for the propagation equations is used to include the ASE effects on the behavior of the amplifier. The results using analytical solutions are achieved faster than using the EDF Dynamic-Full Model, but the results are less accurate. The model which you use depends on the trade off between time and accuracy. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 5 m — [0, 1e4] 10 ms — ]0, +INF[ 0.01 dB/m — [0,100] 0.015 dB/m — [0,100] Specifies the doped fiber length Er metastable lifetime Specifies the Erbium metastable lifetime Loss at 1550 nm Determines the fiber loss at 1550 nm Loss at 980 nm Determines the fiber loss at 980 nm 509 EDF DYNAMIC—ANALYTICAL MODEL Name and description Default value Default unit Units Value range Input data Fiber specification — — Fiber specification, Saturation parameter 4.4e+015 1/(s.m) — [1e-10, +INF[ 0.24 — — [0.1,1] 1e+025 m–3 m–3~ppm-wt ~wt% [1,+INF[ 2.2 μm — [0,1, 10] 2.2 μm — [0.1, 10] Name and description Default value Units Value range OptiAmplifier format False — True, False nm — nm, m, Hz, THz Erbium.dat — — Name and description Default value Units Value range Relative error 0.0001 — ]0,1] 100 — [10,10000] Determines if saturation parameter is used or not Saturation parameter Specifies value of saturation parameter Numerical aperture Specifies the numerical aperture of the Er-doped fiber Er ion density Specifies the Er doping in the Er-doped fiber Core radius Specifies the fiber core radius Er doping radius Species the Erbium doped radius Cross-sections Determines the format of the OptiAmplifier file File frequency unit Determines the frequency unit of the file with the measurements Cross-section file name Determines the cross-section file Numerical Determines the relative error acceptable in each calculation for the steady-state solution used as initial condition for the dynamic behavior Max. number of iterations Specifies the maximum number of times to repeat the longitudinal integrations for the powers when solving the steady-state equations used as initial condition for the dynamic behavior 510 EDF DYNAMIC—ANALYTICAL MODEL Name and description Default value Units Value range Longitudinal steps 100 — [10,10000] Determines the number of longitudinal steps in the calculation Overlap factor data Calculate Calculate, Load from file LP01 Marcuse Gaussian, Whitley Gaussian, Desurvire Gaussian, Myslinski Gaussian, LP01 Determines whether the overlap factor values will be calculated by the component or it will be loaded from a file Geometrical model Determines whether the component will calculate the overlap factor using one of the gaussian approximations, or the LP01 mode Overlap factor file name OverlapFactor. dat Specifies the overlap factor file name Reference time 0.5 / ( Bit rate ) s [0,1e10] Name and description Default value Units Value range Enabled True — True, False Determines the instant of time used to take the powers to use as input powers in the fiber to solve the steady-state regime that will determine the initial values Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30,30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 GHz Hz, GHz, THz, nm [1,1000] –100 dB — ]-INF,0[ Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins spacing Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins 511 EDF DYNAMIC—ANALYTICAL MODEL Name and description Default value Default unit Units Value range Noise dynamic 3 dB — [0,+INF[ Convert noise bins — — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description X Title Y Title Absorption parameters Wavelength (m) Cross-section (m2) Emission parameters Wavelength (m) Cross-section (m2) Average population density N2 Time (s) N2 Technical background This model uses analytical solutions for the same rate and propagation as [1], Equation 2, and Equation 3 described in Erbium Doped Fiber. These equations consider a two-level system interacting with light. As with the EDF Dynamic-Full Model, it's assumed in this analytical model that the signal and pump powers change slowly compared to the optical transit time along the fiber. Neglecting the ASE and the background loss in Equation 1, Equation 2, and Equation 3 for the Erbium Doped Fiber [1]: ± N ∂N 2 ( z ,t ) N 2 ( z ,t ) ∂P n ( z ,t ) 1 -------------------- = – ----------------- – ----------- ∑ u j ---------------------∂t τ ρA eff n = 1 ∂z (1) 512 EDF DYNAMIC—ANALYTICAL MODEL and ∂P n ( z ,t ) e a a -------------------- = u n { ρΓ n [ ( σ n + σ n )N 2 ( z ,t ) – σ n ] }P n ( z ,t ) ∂z (2) where all the parameters were defined in Erbium Doped Fiber. Integrating Equation 1 and Equation 2 over z from 0 to L and defining N 2 as the total number of erbium ions in the upper state: L N 2 ( t ) = ρA eff ∫ N 2 ( z ,t ) dz 0 (3) we have dN 2 ( t ) – N 2 ( t ) N ±out ± in ---------------- = ---------------- – ∑ P n ( t ) – P n ( t ) dt τ n=1 (4) and ± out Pn ± in ( t ) – Pn ( Gn – 1 ) (5) where e a a G n = exp { Γ n [ ( σ n + σ n )N 2 ( z ,t ) – ρσ n ]L } (6) A further approximation enables us to estimate the ASE effects on this model. Considering N2(z) constant at each instant of time (which is a good approximation for strongly inverted EDFA), the propagation equations have an analytical solution which gives [2]: ± out Pn ± in ± in sp ( t ) – P n ( t ) = Pn ( t ) [ G n ( t ) – 1 ] + 2n n [ G n ( t ) – 1 ]Δν ASE (7) 513 EDF DYNAMIC—ANALYTICAL MODEL where sp nn e N 2 ( t )σ n = --------------------------------------------e a a ( σ n + σ n )N 2 – σ n ρ (8) is called the spontaneous emission factor. Substituting Equation 8 for Equation 4, we finally obtain: dN 2 ( t ) –N2 ( t ) --------------- = ---------------– dt τ N ∑ n=1 ± in Pn ( t ) [ Gn ( t ) N sp – 1 ] + ∑ 4n n [ Gn ( t ) – 1 ]Δν ASE n (9) This module uses Equation 5 and Equation 9 to simulate the dynamic behavior of the amplifier. Once given an initial value for the total number of excited ions, that is, N 2 (t=0), and the input powers at each time, these coupled equations can be solved with an interactive loop between them. Numerical solution As initial values for the total population of the upper level, the program solves the steady-state case. The parameter reference time determines the instant of time used to take the powers that will be used as input powers in the fiber in order to solve the equations in the steady-state regime. The obtained results will determine the initial value for the total number of excited erbium ions at t=0 ( N 2 (t=0)). In this way, when the calculation of the dynamic behavior to the sampled signal and pump channels starts at t=0, the program assumes that the population inversion is already different from zero, and the value of the upper level population is given at t=0 by the powers at the reference time. Generally speaking, it is interesting to determine the behavior of the amplifier in scales of time that go from a few microseconds to tens of milliseconds. It is important to set the bit rate and the sequence length of the simulations in such a way that the time windows obey this requirement. If the time windows in your simulations are too short (for example, by a few nanoseconds), the gain of the EDF Dynamic amplifier will be given at almost all instants by the gain that one amplifier operating in the steadystate regime with the inputs powers given by the reference time would have, because the time response scales in EDFA are always in the order of microseconds or longer. The parameterized channels and noise bins input powers are considered constant in time. The output powers for these channels are calculated averaging in time N 2 . This means that during the calculation, the program saves the values of N 2 at each instant of time and then calculates the medium value ⟨ N 2⟩ . Equation 4 and ⟨ N 2⟩ are then used to calculate the output powers of the parameterized and noise channels. 514 EDF DYNAMIC—ANALYTICAL MODEL References [1] Y. Sun, J.L. Zyskind, and A.K. Srivastava, "Average Inversion Level, Modeling, and Physics of Erbium-Doped Fiber Amplifiers," Journal of Selected Topics in Quantum Electronics, Vol. 3, N. 4, pp. 991-1006, 1997. [2] T. Georges and E. Delevaque, "Analytical Modeling of High-Gain Erbium-Doped Fiber Amplifiers," Optics Letters, Vol. 17, N. 16, pp. 1113-1115, 1992. 515 EDF DYNAMIC—ANALYTICAL MODEL Notes: 516 EDFA EDFA Designs Er-doped fiber amplifiers by considering numerical solutions of the rate and the propagation equations under stationary conditions. The model includes amplified spontaneous emission (ASE) as observed in the amplifier Erbium Doped Fiber. However, this module allows you to select forward and/or backward pump, as well as the pump power values. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Core radius 2.2 µm — [0.1,10] 2.2 µm — [0.1,10] 10 ms — [0.01,100] 0.24 — — [0.1,1] 1e+025 m–3 m–3~ppmwt~wt% [1,+INF[ 0.1 dB/cm — [0,100] 0.15 dB/cm — [0,100] Determines the Er-doped fiber core radius Er doping radius Specifies the Er-doped radius Er metastable lifetime Determines the Er metastable lifetime Numerical aperture Specifies the numerical aperture of the Er-doped fiber Er ion density Specifies the Er doping in the Er-doped fiber Loss at 1550 nm Determines the fiber loss at 1550 nm Loss at 980 nm Determines the fiber loss at 980 nm 517 EDFA Name and description Default value Default unit Units Value range Length 5 m — [0,10000] Determines the Er-doped fiber length Pumping Name and description Default value Default unit Units Value range Forward pump power 100 mW W, mW, dBm [0,+INF[ 0 mW W, mW, dBm [0,+INF[ 980 nm — [700,1600] 980 nm — [700,1600] Name and description Default value Units Value range File frequency unit nm — nm, m, Hz, THz False — True, False Erbium.dat — — Name and description Default value Units Value range Relative error 0.0001 — ]0,1] 50 — [10,10000] Determines the co-propagating pump power Backward pump power Determines the counter-propagating pump power Forward pump wavelength Determines the co-propagating pump wavelength Backward pump wavelength Determines the counter-propagating pump wavelength Cross-sections Determines the frequency unit of the file with the measurements OptiAmplifier format Determines the format of the OptiAmplifier file cross-section file name Determines the cross-section file Numerical Determines the relative error acceptable in each calculation Max. number of iterations Specifies the maximum number of times to repeat the calculation 518 EDFA Name and description Default value Units Value range Longitudinal steps 100 — [10,10000] Determines the number of longitudinal steps in the calculation Polarization Name and description Default value Units Value range Polarization filter None — None, Polarization X, Polarization Y Name and description Default value Units Value range Enabled Yes — [0, 0] Determines the polarization of the filter Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30] 13 THz Hz, Thz, nm [1e-100, 1e-100] 125 GHz Hz, GHz, THz, nm [1,1] –100 dB — [-1e+100, -1e+100] 3 dB — [0, 0] Convert noise bins — — [0, 0] Determines the noise center frequency Noise bandwidth Bandwidth to increase noise bins Noise bins spacing Determines noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal 519 EDFA Random numbers Name and description Default value Units Value range Generate random seed Yes — [0, 0] 0 — [0, 0] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description X Title Y Title Absorption parameters Wavelength (m) Cross-section (m2) Emission parameters Wavelength (m) Cross-section (m2) Technical background The routines in EDFA numerically solve the rate equations coupled with propagating equations under stationary conditions. It is assumed a two-level Er system approximation and the rate equations are based on the energy level diagram. The same expressions described in the module Erbium Doped Fiber are adopted by this model. The main difference is related to the amplifier pump scheme selection. You can choose co-propagating, counter-propagating, or bi-directional pump schemes with the option to set wavelength and pump power. Geometrical Er-doped fiber parameters and cross-section curves are required as input files. As output files, you can access gain, output power values, and noise figure determined in the ASE bandwidth set as noise input data. Er Doped Fiber rate and propagation equations The lifetime transition from level 4I11/2 is of the order of microseconds for silicate hosts. Therefore, it is reasonable to neglect the population density N3 in the rate equations description. A two-level system approximation is used in this case. Under the assumption of the normalized population densities N1 and N2 at the ground and metastable energy level, 4I15/2 and 4I13/2 populations are calculated by numerically solving the rate and propagation equations[1]: ∂N 2 ( z ,t ) N 2 ( z ,t ) 1 N e a a + – -------------------- = – ---------------- – ------- ∑ { Γ n [ ( σ n + σ n )N 2 ( z ,t ) – σ n ] } [ P n ( z ,t ) + P n ( z ,t ) ] ∂t τ A eff n = 1 (1) 520 EDFA N2 + N1 = 1 (2) ± ∂P n ( z ,t ) e a a ± e ---------------------- = u n { ρΓ n [ ( σ n + σ n )N 2 ( z ,t ) – σ n – α ] }Pn ( z ,t ) + 2ρΔνN 2 Γ n σ n ∂z (3) where the optical powers are expressed in units of number of photons per unit time, τ is the metastable spontaneous emission lifetime, N is the number of channels taken into account in the simulation (including signals, pumps, and ASE bins), ρ is the number density of the active erbium ions, α is the attenuation coefficient (which takes into account the background loss of the fiber), Δν is the frequency step used in the simulation to resolve the ASE spectrum, and Aeff is the effective doped area given 2 by π × b , where b is the Er doping radius (it is considered a uniform distribution of erbium ions in the area given by the Er doping radius region). λ n has optical power Pn(z,t) at location z and time t, e a with emission and absorption cross-section σ n and σ n respectively, and confinement factor Γ n . The superscript symbols + and – are used to indicate The nth channel of wavelength channels traveling in forward (from 0 to L) and backward (from L to 0) directions, respectively. For beams traveling in the forward direction the opposite direction u n = 1 and for beams in u n = – 1. The overlap integrals Γ n between the LP01 mode intensity (which is used in this program) distribution doped region area are given by: b ∫ E ( r ,ν ) 2 ∫ E ( r ,ν ) 2 r dr 0 Γ n ( ν ) = --------------------------------∞ r dr 0 (4) where E(r, ν ) gives the electric density field. Solving Equation 1, Equation 2, and Equation 3 under stationary conditions allows you to determine the amplifier performance features. The fiber parameters such as core and Er doping radius, Er metastable lifetime, numerical aperture, Er ion density, loss at 980 nm and 1550 nm, and the fiber length are required as input values. The absorption and emission cross-section are also required as input files. 521 EDFA Absorption and Emission cross-sections There are two options available to you to prepare the cross-section file, which is specified in an ASCII file. The first option is to provide the cross-section input file in three columns. The first column refers to the wavelength in [m], [nm], [Hz] or [THz] units. The second column gives the absorption cross- section in [m2] units. The third column gives the emission cross-section in [m2] units. In this case, the cross-section file format is: λ (nm) σ [m ] σ [m ] 929.982 9.28e-27 0 930.172 7.05e-27 0 1029.972 2.85e-27 0 1030.072 3.59e-27 0 1450.6 2.086e-26 1.726e-27 1450.8 2.186e-26 1.823e-27 1649.8 1.540e-26 8.228e-26 1650.0 1.540e-26 8.280e-26 a 2 e 2 . . . . . . The second option is to consider the absorption and emission coefficients (or Giles parameters) as input parameters that are converted to cross-section by internal routines in the software. This is especially interesting when only Giles parameters are measured to the Er-doped fiber. The file format in this case contains three columns. The first column refers to the wavelength in [m], [nm], [Hz] or [THz] units. The second column gives the absorption coefficient in [dB/m] units. The third column gives the emission coefficient in [dB/m] units. An example of this input file is: λ (nm) α (dB/m) g* (dB/m) 929.982 0.39168 0 930.172 0.2856 0 –0.05508 0 . . . 1029.972 522 EDFA λ (nm) α (dB/m) g* (dB/m) 1030.072 –0.14484 0 1450.6 1.8075 0.35599973 1450.8 1.815 0.360619883 1649.8 0.005 0.484116259 1650.0 –0.0175 0.477803876 . . . where the wavelength is given in [nm] units, absorption and emission coefficients are in [dB/m]. 523 EDFA Reference: [1] C.R. Giles and E. Desurvire, “Modeling erbium-doped fiber amplifiers,” Journal of Lightwave Technology, Vol. 9, N. 2, pp. 271-283, 1991. 524 OPTICAL AMPLIFIER Optical Amplifier Enables the design of amplifiers, including EDFAs, that consider pre-defined operational conditions. This means that expected gain, noise figure, and amplifier output power can be previously specified. The amplifier presents the same facilities as a black box model, which enables you to select the operation mode with gain control, power control, or to perform simulations under saturated conditions, as well as define the expected amplifier performance. It is specially suited to perform prompt performance analysis of one or cascaded amplifiers in a long-haul system. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Operation mode Gain control — — Gain control, Power control, Signal power control, Saturation 20 dB — [0,100] 10 dBm W, mW, dBm [-100,100] 10 dBm — [-100,100] Output — — Input, Output Amplifier operation mode Gain Determines the signal gain Power Determines the signal output power Saturation power Specifies the optical power at the gain compressed by 3 dB Saturation port Determines the amplifier saturation port 525 OPTICAL AMPLIFIER Name and description Default value Default unit Units Value range Include noise YES — — — Noise figure 4 dB — [3,100] Name and description Default value Units Value range Polarization filter None — None, Polarization X, Polarization Y Name and description Default value Units Value range Enabled True — True, False Determines the amplifier noise figure Polarization Determines the polarization of the filter Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 3e+006] Noise bandwidth 13 THz Hz, THz, nm [1e-100, 1e+100] Noise bins spacing 125 GHz Hz, GHz, THz, nm [1,1000] Convert noise bins — — True, False Name and description Default value Units Value range Generate random seed True — True, False Specifies the noise bins spacing Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique 526 OPTICAL AMPLIFIER Name and description Default value Units Value range Random seed index 0 — [0,4999] User-defined seed index for noise generation Technical background The simulation of the flat gain amplifier is performed in the opposite way than that used by the previous described models. In this case, the desired amplifier performance given by the gain, the output power, the saturated output power, and the noise figure values are used as input parameters to design the amplifier. The input data are related by the propagation equation written in terms of the parameter required in each mode selected. There are three different mode controls — Gain control, Power Control, and Saturation. Large and small input signal can be considered in this amplifier model. The concept of the flat gain amplifier enabling you to define the device performance makes this model flexible to design amplifiers considering different applications in a system such as booster, in-line, and preamplifier. The amplified spontaneous emission is included in the model of the Flat Gain EDFA and it is built from the noise figure input value. Operation Modes The Flat Gain EDFA subsystem enables three operation modes, which you can select in the Flat Gain EDFA Properties dialog box by clicking on Main/Operation Mode/Value. The first option is the Gain Control that maintains the gain constant and allows you to include (or not include) the amplified spontaneous emission in the calculations. In the second operation mode option, Power Control, the value of the output power is maintained constantly. The third operation mode, Saturation, considers the amplifier operating in a saturated condition — operating in an output signal power correspondent to a gain 3 dB lower than the saturated gain. Gain Control mode In this mode, you set the desired amplifier gain (in dB units), which is given by the ratio of the total output power (Pout) and total input power (Psin), including (or not including) the generated ASE (PASE), as given by Equation 1. There are no additional iterations or complicated equation solutions in this mode. The set amplifier input parameters as gain and noise figure give the performance of this sub-system to be inserted in the global system. ( P out – P ASE ) G = -------------------------------P sin (1) Power Control mode 527 OPTICAL AMPLIFIER The value that you define in the power control mode is the desired amplifier output power (in dBm units), which is maintained constantly. If the gain required to keep the desired output power is higher than the value of the parameter Gain, the amplifier will saturate, and the maximum power will be determined by the input power amplified by the parameter Gain. Analogous with the gain-controlled mode, there is no additional calculation involved in the designed amplifier. The output power set as input parameter defines the amplifier performance to be considered in the system where this amplifier is inserted. The ASE, which basically computes the noise introduced by the amplifier into the system, can be included (or not included) in the amplifier performance. Note that the specified output power is not degraded by the ASE noise included in the amplifier subsystems — however, this noise source is computed in the global system analysis. Signal power control mode will not include the input noise into the calculated input power. Saturation mode In the saturation mode, it is assumed that the pump power is constant, causing the amplifier to operate in a saturated regime. The saturation power, gain, and noise figure are the parameters required by this mode. The saturation power is the input parameter maintained constant in this mode selection, and in an ASE-free model can be related with the gain (G), output power (Pout), and intrinsic saturation power (Psatint) by the expression: – 1- P out G = G 0 exp – G -------------------G P int sat (2) where G0 is the small-signal gain or unsaturated gain. The intrinsic saturation power is written as: int ---------Psat = Ahv σa τ (3) where A is the mode-field area, h is the Planck’s constant, ν is the frequency at the propagating signal, σa is the absorption cross-section, and τ is the Er metastable lifetime in silica. These fiber specifications are not required in this amplifier module, since the intrinsic saturation power will be related to the amplifier saturation power under the gain compression condition. Under the 3 dB gain compression, the output power is proportional to the intrinsic saturation power. This relation is: P out 3dB Compressed int = In ( 2 )P sat (4) 528 OPTICAL AMPLIFIER ASE calculation The ASE noise spectrum is built in this model from the noise figure provided as input parameter, considering the expression that relates spectral ASE noise with noise figure. The noise figure (NF) evaluated at a specific signal wavelength is: S out 1- + --------NF = --G Ghv (5) The term 1/G corresponds to the shot noise, Sout is the output ASE spectral density at the signal wavelength, and hν is the photon energy. In practical cases, there is ASE present at the input of the doped fiber so that the amplified input ASE must be added to the output ASE spectral density. The output ASE can be written as: S out = S amp + S in × G (6) where Samp is the spectral density ASE generated by the doped fiber. Correcting for the input ASE gives the signal-spontaneous beat noise limited noise figure as a function of the signal gain, and input and output ASE spectral densities: Sout S in 1- + --------NF = --- – -----G Ghv hv (7) In the signal-spontaneous beat noise limited regime, with high gain and negligible input coupling, the noise figure of the optical preamplifier approaches a theoretical limit of [1]: 2 NF opt σ sig – sp = ---------------------------------- = 2n sp 2 2 σ sig – sh ( in )G (8) where the spontaneous emission factor, nsp, is defined as: N2( z ) n sp ( v ,z ) = -------------------------------------------N 2 ( z ) – N 1 ( z )ε ( v ) (9) where σa ( v ) ε ( v ) = ------------σe ( v ) (10) Since nsp ≥ 1, an EDFA at high gain has a minimum noise figure of 3 dB. This is derived by assuming that the input signal is shot noise limited and the output noise is signal-spontaneous beat noise limited. In practical situations, the noise figure is degraded by the amplifier input coupling loss. 529 OPTICAL AMPLIFIER Noise figure This lists the signal-spontaneous beat noise limited noise figure. For each signal wavelength, the noise figure is: NoiseFigure ( dB ) = 10 × log 10 1- + S------------------out ( λ s ) S in ( λ s ) --– ----------------G Ghv hv (11) where S out ( λ s ) is the output ASE spectral density (W/Hz) at the signal wavelength, and S in ( λ s ) is the input ASE spectral density at the signal wavelength. Rewriting the ASE spectral density as a function of noise figure value, the noise spectrum can be generated considering the noise figure input parameter. Therefore, the ASE spectrum is obtained from the expression: S out ( λ s ) = G × hv 10 NoiseFigure ( dB ) ------------------------------------10 1- – S---------------in ( λ s ) – --hv G (12) References [1] T. Okoshi, "Exact Noise-Figure Formulas for Optical Amplifiers and Amplifier-Fiber Cascaded Chains," IEEE/OSA Topical Meeting on Optical Amplifiers and their Applications, Monterrey, PDP11, 1990. 530 EDFA MEASURED EDFA Measured Enables you to design EDFAs considering pre-defined operation conditions that mean to specify previously the measured gain, noise figure, and amplifier output power. It is specially indicated for the prompt performance analysis of one or cascaded amplifiers present in a long-haul system. It can be also used for flat gain amplifiers. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Measured gain and noise figure (nm dB dB) — — — GainAndNF.dat — — — 25 dBm W, mW, dBm [-100,+100] True — — True, False Wavelength, gain, and NF table with the measured data Gain and noise figure file name Filename with the measured data Max. output power Determines the total signal output power Include noise Determines if the component add noise to the output signal 531 EDFA MEASURED Polarization Name and description Default value Units Value range Polarization filter None — None, Polarization X, Polarization Y Name and description Default value Units Value range Enabled Yes — [0, 0] Determines the polarization of the filter Simulation Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30] 13 THz Hz, Thz, nm [1e-100, 1e100] 125 GHz Hz, GHz, THz, nm [1, 1] –100 dB — [-1e+100, 1e+100] 3 dB — [0, 0] Convert noise bins — — [0, 0] Name and description Default value Units Value range Generate random seed Yes — [0, 0] Determines the noise center frequency Noise bandwidth Bandwidth to increase noise bins Noise bins spacing Determines noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique 532 EDFA MEASURED Name and description Default value Units Value range Random seed index 0 — [0, 4999] User-defined seed index for noise generation Technical background The simulation of the EDFA Measured is performed in similar way to the Flat Gain EDFA. In this case, the desired amplifier performance given by the measured gain, noise figure, and maximum output power. Large and small input signals can be considered in this amplifier model. The concept of the measured amplifier enabling you to define the device performance makes this model flexible to design amplifiers for different applications in a system such as booster, in-line, pre-amplifier, gain flat, and noise flat. It can also load measurements from other software tools such as Optiwave's OptiAmplifier. This maximum output power can be limited when the total output power is greater then the parameter Max. output power. The calculation engine reduces the amplifier gain in order to have the total output power equal to the parameter Max. output power. ASE calculation The ASE noise spectrum is built in this model from the noise figure provided as input parameter, considering the expression that relates spectral ASE noise with noise figure. The noise figure (NF) evaluated at a specific signal wavelength is: S out 1- + --------NF = --G Ghv (1) The term 1/G corresponds to the shot noise, Sout is the output ASE spectral density at the signal wavelength, and hν is the photon energy. In practical cases, there is ASE present at the input of the doped fiber so that the amplified input ASE must be added to the output ASE spectral density. Therefore, the output ASE can be written as: S out = S amp + S in × G (2) where Samp is the spectral density ASE generated by the doped fiber. Correcting for the input ASE gives the signal-spontaneous beat noise limited noise figure as a function of the signal gain, and input and output ASE spectral densities: Sout S in 1- + --------NF = --- – -----G Ghv hv 533 EDFA MEASURED (3) In the signal-spontaneous beat noise limited regime, with high gain and negligible input coupling, the noise figure of the optical preamplifier approaches a theoretical limit of [1]: 2 NF opt σ sig – sp = ---------------------------------- = 2n sp 2 2 σ sig – sh ( in )G (4) where the spontaneous emission factor, nsp, is defined as: N2( z ) n sp ( v ,z ) = -------------------------------------------N 2 ( z ) – N 1 ( z )ε ( v ) (5) where σa ( v ) ε ( v ) = ------------σe ( v ) (6) Since nsp ≥ 1, an EDFA at high gain has a minimum noise figure of 3 dB. This is derived by assuming that the input signal is shot noise limited and the output noise is signal-spontaneous beat noise limited. In practical situations, the noise figure is degraded by the amplifier input coupling loss. Noise figure This lists the signal-spontaneous beat noise limited noise figure. For each signal wavelength, the noise figure is: NoiseFigure ( dB ) = 10 × log 10 1- S out ( λ s ) S in ( λ s ) --+ ------------------- – ----------------G Ghv hv (7) where S out ( λ s ) is the output ASE spectral density (W/Hz) at the signal wavelength, S in ( λ s ) is the input ASE spectral density at the signal wavelength. Rewriting the ASE spectral density as a function of noise figure value, the noise spectrum can be generated considering the noise figure input parameter. Therefore, the ASE spectrum is obtained from the expression: S out ( λ s ) = G × hv 10 NoiseFigure ( dB ) ------------------------------------10 1- Sin ( λ s ) – --– ----------------G hv (8) 534 EDFA MEASURED Measurements You can provide the measurements in the parameter Measured gain and noise figure. Alternatively, the measurements can be loaded from a file using the parameter Gain and noise figure file name. The gain and noise figure curves must be provided in the file containing three columns. The first column refers to the wavelength specified in [nm] units. The second column gives the gain noise curve in [dB] units. The third column gives the noise figure in [dB] units. Example of input file: Wavelength ([nm] Gain [dB] NF [dB] 1500.00 20.00 4.00 1510.00 20.00 4.00 1520.00 20.00 4.00 1530.00 20.00 4.00 1540.00 20.00 4.00 1550.00 20.00 4.00 535 EDFA MEASURED Reference: [1] T. Okoshi, "Exact Noise-Figure Formulas for Optical Amplifiers and Amplifier-Fiber Cascaded Chains," IEEE/OSA Topical Meeting on Optical Amplifiers and their Applications, Monterrey, PDP11, 1990. 536 ERBIUM DOPED FIBER Erbium Doped Fiber This component simulates a bidirectional Erbium doped fiber considering ESA, Raleigh scattering, ionion interactions, and temperature dependence effects. The component solves numerically the rate and propagation equations in the steady-state case, assuming a two-level Erbium system for an inhomogeneous and homogeneous approach. Ports Name and description Port type Signal type Input1 Input Optical Output1 Output Optical Input2 Input Optical Output2 Output Optical Parameters Main Name and description Symbol Default value Default unit Units Value range Length L 5 m — [0, 1e4] τ 10 ms — ]0, +INF[ — Fiber specification — — Fiber specification, Saturation parameter ζ 4.4e+015 1/(s.m) — [1e-10, +INF[ a 2.2 μm — [0,1, 10] Specifies the doped fiber length Er metastable lifetime Specifies the Erbium metastable lifetime Input data Determines if saturation parameter is used or not Saturation parameter Specifies value of saturation parameter Core radius Specifies the fiber core radius 537 ERBIUM DOPED FIBER Name and description Symbol Default value Default unit Units Value range Er doping radius b 2.2 μm — [0.1, 10] nt 1e+20 m-3 m-3 , ~ppm-wt, ~wt% [1e23, +INF[ NA 0.24 — — [0.1,1] Species the Erbium doped radius Er ion density Specifies the Erbium doping in the fiber Numerical aperture Specifies the numerical aperture of the fiber Cross-sections Name and description Default value Default unit Units Value range OptiAmplifier format False — — True, False nm — — nm, m, Hz, THz Erbium.dat — — — Determines if format of cross-section file is an OptiAmplifier file File frequency unit Determines frequency unit of the file with the cross sections Cross-section file name Specifies Erbium cross-section file name Enhanced Name and description Symbol Default value Default unit Units Value range Background loss data type l(λ) Constant — — Constant, From file l 1310 3 dB/Km [0, +INF[ — Loss.dat — — — False — — True, False Determines if the loss will be calculated from the loss at 1310nm (constant) or it will be loaded from a file Loss at 1310 nm Specifies the fiber loss at 1310nm Background loss file name Specifies loss file name Include Rayleigh backscattering Determines if Rayleigh scattering effect is included or not 538 ERBIUM DOPED FIBER Name and description Symbol Default value Default unit Units Value range Rayleigh Constant KR 150 — dB/Km [0, 1000] C(λ) Calculate — — Calculate, From file — Capture.dat — — — — False — — True, False — Homogeneous — — Homogeneous, Inhomogeneous, Combined Uc 1e-022 mk 2 K Specifies the value of the Rayleigh constant Backscattering capture fraction Determines if capture fraction values are calculated by the component or loaded from a file Rayleigh capture file name Specifies the capture file name Includes ion-ion interaction effects Determines whether Er-Er ion interaction effects are included or not Ion-Ion interaction effect Determines which kind of Er-Er ion interaction is considered Upconversion coefficient 3 m ⁄s [0, 1000] — — [0, 500] 12 — % [0, 100] — False — — True, False T 20 — C [-273, 500] Tm 20 — C [-273, 500] — False — — True, False — ESAErbium.dat — — — Specifies the two-particle upconversion coefficient Ions per cluster Specifies number of ions in a cluster Relative number of clusters Specifies the relative number of clusters Include Temperature Effects Determines if temperature dependence is taken into account Temperature Specifies the current temperature Cross-section Temperature Specifies the temperature when the cross-section was measured Include ESA Effect Determines if excited stated absorption is taken into account ESA Cross-section file name Specifies the ESA cross-section file name 539 ERBIUM DOPED FIBER Name and description Symbol Default value Default unit Units Value range Extract ESA from emission — True — — True, False Name and description Symbol Default value Default unit Units Value range Calculation algorithm — Giles — Saleh, Jopson, Giles, Inhomogeneous ζ 0.0001 — — [1e-100, 1] N max 100 — — [1, 1e8] Determines if the component has to extract the ESA cross-section from the loaded file Numerical Determines algorithm to be used in simulation Relative error Specifies maximum acceptable difference between two consecutive iterations to complete the iteration process Max. number of iterations Specifies the maximum number of iterations executed Number of longitudinal steps 50 [1, 1e8] Specifies the minimum number of longitudinal steps in the fiber Overlap factor data Γ Calculate — — Calculate, From file — LP01 — — Marcuse Gaussian, Whitley Gaussian, Desurvire Gaussian, Myslinski Gaussian, LP01 — Power independent — — Power independent, Power dependent — 2 — — [1, 50] Determines whether overlap factor values are calculated by the component or loaded from a file Geometrical model Determines whether the component calculates the overlap factor using one of the Gaussian approximations, or the LP01 mode Overlap factor Determines if overlap factor calculations takes into account the signal and pump power Nr. of transverse integrations If PowerDependent is selected for Overlap factor, specifies the number of times that the overlap factor is calculated over the fiber length 540 ERBIUM DOPED FIBER Name and description Symbol Default value Default unit Units Value range Overlap factor file name — Confinement.dat — — — — False — — True, False — 0.001 — — [1E-10, 0.1] Δλ inh 11.5 nm — ]0, 100] nG 17 — — [8, 28] Name and description Default value Default unit Units Value range Calculate graphs False — — True, False Number of distance steps 20 — — [1,1e8] Number of wavelength steps 20 — — [1,1e8] Linear scale True — — True, False Minimum value -50 — dBm ]1e-100, 1e100[ Pump reference wavelength 1400 nm [100, 1900] Specifies the overlap factor file name Generate homogeneous cr. Generate the homogeneous crosssections Inhomogeneous accuracy If the inhomogeneous model is selected, this parameter specifies the accuracy in the convolution integrals Inhomogeneous linewidth Specifies the Erbium-doped fiber inhomogeneous linewidth Number of gaussians Determines number of gaussians used in generation of the homogeneous cross-sections Graphs Simulation Name and description Default value Units Value range Enabled True — True, False False — True, False Determines whether or not the component is enabled Enable reflections Determines whether or not the component launches reflections due to backscattering in the output 541 ERBIUM DOPED FIBER Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30,30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 THz Hz, GHz, THz, nm [1,1000] –100 dB — ]-INF,0[ 3 dB — [0,+INF[ Convert noise bins — — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins spacing Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 542 ERBIUM DOPED FIBER Technical background This module presents a rapid numerical solver for the EDF rate and propagation equations for signals, pumps and amplified spontaneous emission (ASE) considering the steady-state case. The propagation and rate equations of a two level system are used to model the Erbium-doped fiber. Several effects are considered, including Er +3 – Er -3 interactions, excited state absorption, temperature dependence, and background loss. Furthermore, the component assumes the possibility of considering the inhomogeneous broadening in the EDF. Propagation and rate equations The Erbium Doped Fiber component is based on the solution of the rate and propagation equations assuming a two-level model. The use of a two-level model for the amplifier is justified, as for pumping into the 980nm absorption band, the lifetime transition from level 4 11 ⁄ 2 is of the order of microseconds for silicate hosts and is reasonable to neglect the population density N 3 in the rate equations description. At 1480nm, the pumping is direct to the upper sub-levels of the metastable manifold. Rate equations are based on energy levels and describe the effects of absorption, stimulated emission, and spontaneous emission on the populations of the ground ( n 1 ) and metastable ( n 2 ) states. For a two-level system with dn dn – --------1 = --------2 = dt dt k optical beams, the rate equations are given by: σa ( v k ) σe ( v k ) 1 - ⋅ i k ( r, φ ) ⋅ Pk ( z ) ⋅ n 1 ( r, φ, z ) – ∑ ---------------- ⋅ i k ( r, φ ) ⋅ Pk ( z ) ⋅ n 2 ( r, φ, z ) – --- ⋅ n 2 ( r, φ, z ) ∑ --------------hv k hv k τ k (1)a k (1)b n 1 ( r, φ, z ) + n 2 ( r, φ, z ) = n t ( r, φ, z ) h is the Planck constant, τ is the metastable lifetime parameter, v k is the frequency, and P k is the power of the k th beam. The absorption and emission crosssection of the k th beam are σ a ( v k ) and σ e ( v k ) , respectively, and n t is the local erbium ion density. The normalized optical intensity i k ( r, φ ) is defined as i k ( r, φ ) = I k ( r, φ, z ) ⁄ P k ( z ) , where I k ( r, φ, z ) is light intensity distribution of the k th beam. where 543 ERBIUM DOPED FIBER The propagation equations describe the propagation of the beams through the doped fiber, and are given by: dP --------k- = u k ⋅ σ e ( v k ) ⋅ ( P k ( z ) + P 0k ) ⋅ dt 2π ∞ ∫ ∫ n2 ( r, φ, z ) ⋅ ik ( r, φ ) ⋅ r ⋅ dr ⋅ dφ – uk ⋅ σa ( vk ) ⋅ Pk ( z ) . 0 0 (2) 2π ∞ . ∫ ∫ n 1 ( r, φ, z ) ⋅ ik ( r, φ ) ⋅ r ⋅ dr ⋅ dφ 0 0 where each beam propagates in the forward ( u k = 1 ) or backward ( u k = – 1 ) P 0k means the spontaneous emission contribution from the local metastable population n 2 . P 0k = m ⋅ h ⋅ v k ⋅ Δv k , where the normalized number of modes m is normally 2, and Δv k is the noise bandwidth. direction, and Setting the time derivative in Equation 1a to zero and using Equation 1b, the problem is reduced to the steady-state case and the metastable population is defined as: n σa ( vk ) ⋅ τ - ⋅ i k ( r, φ ) ⋅ P k ( z ) ∑ ---------------------hv k k=1 n 2 ( r, φ, z ) = n t ⋅ ------------------------------------------------------------------------------------------------------------n ( σa ( vk ) + σe ( vk ) ) ⋅ τ - ⋅ i k ( r, φ ) ⋅ P k ( z ) + 1 ∑ ------------------------------------------------hv k k=1 With the specified boundary conditions at z = 0 and z = L , Equation 2 and Equation 3 can be integrated over space and frequency. 544 (3) ERBIUM DOPED FIBER Figure 1 Example of absorption and emission cross-sections It is important realize to that the transverse shape of the optical mode and its overlap with the erbium ion distribution profile are very important. It can be parameterized by a factor known as overlap integral factor. Considering a steady-state case, and substituting Equation 1b in Equation 1a, the rate equation becomes: σa ( vk ) σa ( vk ) 1 - ⋅ ik ( r, φ ) ⋅ P k ( z ) ⋅ n t ( r, φ, z ) – ∑ ---------------- ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 2 ( r, φ, z ) – --- ⋅ n 2 ( r, φ, z ) – ∑ --------------hv k hv k τ k k – (4) σe ( vk ) 1 - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 2 ( r, φ, z ) – --- ⋅ n 2 ( r, φ, z ) ∑ --------------hv k τ k Integrating Equation 4 over space: 2π ∞ 2 1 --- ⋅ n 2 ( r, φ ) ⋅ π ⋅ b eff = τ ∫ ∫ ik ( r, φ ) ⋅ n t ( r, φ ) ⋅ r ⋅ dr ⋅ dφ σa ( vk ) 0 0 - ⋅ P k ( z ) ⋅ n t ⋅ ----------------------------------------------------------------------------– ∑ --------------hv k n k t 2π ∞ . ∫ n σa ( vk ) - ⋅ Pk ( z ) ⋅ n2 . ∑ --------------hv k k=1 2π ∞ ∫ ik ( r, φ ) ⋅ n 2 ( r, φ ) ⋅ r ⋅ dr ⋅ dφ 0 0 ----------------------------------------------------------------------------- n2 n – ∑ k=1 ∫ ∫ ik ( r, φ ) ⋅ n2 ( r, φ ) ⋅ r ⋅ dr ⋅ dφ σe ( v k ) 0 0 ---------------- ⋅ P k ( z ) ⋅ n 2 . ----------------------------------------------------------------------------hv k n 2 545 ERBIUM DOPED FIBER where n i is considered the average density, and is given by: 2π ∞ ∫ ∫ ni ( r, φ ) ⋅ r ⋅ dr ⋅ dφ ni( z ) = and (5) 0 0 -----------------------------------------------------2 π ⋅ b eff b eff is the equivalent radius of the doped region: π 1 --⎞2 ⎛ nt ( r ) b eff = = ⎜ 2 ∫ ----------- ⋅ r ⋅ dr⎟ ⎝ nt ( 0 ) ⎠ 0 when the ion density population is uniform, the effective radius is equal to the doped radius, b . For an effective doped radius A eff = π ⋅ 2 b eff . beff , the effective cross-sectional area is Then, the overlap integral or confinement factor for the th i level can be defined as: 2π ∞ ∫ ∫ ik ( r, φ ) ⋅ ni ( r, φ ) ⋅ r ⋅ dr ⋅ dφ Γ kj ( z ) = ni If the erbium ions are well confined to the center of the optical modes, then Γ k, 2 are nearly equal, and can be replaced with the single constant Γ k . 546 (6) 0 0 ---------------------------------------------------------------------------- Γ k, 1 and ERBIUM DOPED FIBER Therefore, using the definition of overlap integral, the average population density for the level 2 is given by: n σa ( vk ) - ⋅ P k ( z ) ⋅ nt ⋅ Γk ∑ --------------hv k k=1 n 2 ( z ) = --------------------------------------------------------------------------------------------------n σ ( v ) + σ ( v ) 1--- ⋅ A – a k e k ------------------------------------- ⋅ Pk ( z ) ⋅ Γk τ eff ∑ hv k (7) k=1 and the propagation equation becomes: dP ---------k = ( σ e ( v k ) + σ a ( v k ) ) ⋅ Pk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ Pk ( z ) ⋅ n t ⋅ Γ k + P0k ⋅ σ e ( v k ) ⋅ n 2 ⋅ Γ k dz (8) Basically, Equation 7 and Equation 8 are the equations solved in the homogeneous case. Slight modifications are made to these equations in order to include other effects. 547 ERBIUM DOPED FIBER Giles-Desurvire Propagation and Rate equations A simpler method of fiber characterization can be done by writing the amplifier equations in terms of Er +3 absorption coefficient ( α k ), gain coefficient ( g k ), and a fiber saturation parameter ( ζ ). These parameters can be obtained by conventional fiber measurement techniques [1]. The saturation parameter ζ = π⋅ 2 b eff ζ can be defined theoretically as: ⋅ nt ⁄ τ and the absorption and gain coefficients are expressed in terms of distributions of the ions and optical modes: 2π ∞ αk ( λk ) = σa ( λ k ) ⋅ ∫ ∫ ik ( r, φ ) ⋅ nt ( r, φ, z ) ⋅ r ⋅ dr ⋅ dφ 0 0 2π ∞ gk ( λk ) = σe ( λk ) ⋅ ∫ ∫ ik ( r, φ ) ⋅ nt ( r, φ, z ) ⋅ r ⋅ dr ⋅ dφ 0 0 For a uniform ion distribution the absorption and gain coefficients can be simplified as: αk ( λk ) = Γ ( λ k ) ⋅ nt ⋅ σa ( λ k ) gk ( λk ) = Γ ( λk ) ⋅ nt ⋅ σe ( λ k ) Giles and Desurvire in [1] rewrote the propagation Equation 8 in terms of saturation parameter, and absorption and emission coefficients: ⎛ ⎞ n n dP k ( z ) ---------------- = u k ⋅ P k ( z ) ⋅ ⎜ g k ( ( v k ) + α k ( v k ) ) ⋅ ----2- – α k ( v k ) – l k⎟ + u k ⋅ P 0k ⋅ g k ( v k ) ⋅ ----2dz ⎝ ⎠ n n t where l k is the background loss. 548 t (9) ERBIUM DOPED FIBER In the same way, the steady-state solution of rate Equation 7 was rewritten as: n Pk ( z ) ⋅ αk vk ∑ ---------------------------h ⋅ vk ⋅ ζ n2 k=1 ----- ( z ) = ------------------------------------------------------------------------------n Pk ( z ) ⋅ ( αk ( vk ) + g k ( v k ) ) nt 1 + ∑ -----------------------------------------------------------hv k (10) k=1 Note: The equation for including ASE. n 2 ( z ) sums over all forward and backward beams, Equation 9 and Equation 10 are referenced further as a Giles model. These equations are solved in the homogeneous line broadening case. The Giles model provides a full spectral solution. The propagation Equation 9 is integrated back and forth along the fiber, in an iterative numerical process, until the solution converges, or the maximum number of iterations ( N max ) is reached. The propagation equation solved by the Giles model can be slightly different from Equation 9, depending on which effects the user has considered in the simulation, such as ESA and Rayleigh scattering. Equation 10 can be different depending on whether the user takes into account the Er +3 – Er +3 interactions. Overlap Integrals The value of the overlap integral can be calculated using Equation 6. The transverse optical modes distributions are described by their normalized optical intensity. For a single-mode fiber, the optical mode can be approximated by the distribution: i ( r, φ ) = LP01 mode vJ 0 ( ur ⁄ a ) 2 --1- ------------------------- r<a π aVJ 1 ( u ) (11) uK 0 ( vr ⁄ a ) 2 --1- -------------------------- r≥a π aVK 1 ( v ) 549 ERBIUM DOPED FIBER a is the fiber core radius, the fiber number V is 2 2 V = 2 ⋅ π ⋅ a ⋅ ( n core – n clad ) ⁄ λ , u and v are the eigenvalues found by matching the solutions at r = a , J 0 is the Bessel function of the first kind of order 0, J 1 is the Bessel function of the first kind of order 1, K 0 is the modified Bessel function of the second kind of order 0, and K 1 is the modified Bessel function of the second kind of where order 1. The LP01 mode distribution can also be approximated with a Gaussian function: 2 2 - exp ⎛ – 2----------⋅ r -⎞ i ( r, φ ) = --------⎜ ⎟ 2 ⎝ w2 ⎠ πw where the Gaussian mode radius, (12) w Gauss , has been given by various authors as: w Gauss = a ⎛⎝ 0.65 + 1.619 ------------- + 2.879 -------------⎞⎠ Marcuse 1.5 6 V V w Gauss = a ⎛ 0.616 + 1.66 ---------- + 0.987 -------------⎞ Whitley ⎝ 1.5 6 ⎠ V V w Gauss = a ⎛ 0.759 + 1.289 ------------- + 1.041 -------------⎞ Desurvire ⎝ 1.5 6 ⎠ V V 1.237- + 1.429 w Gauss = a ⎛ 0.761 + ------------------------⎞ Myslinski ⎝ 1.5 6 ⎠ V V (13) (14) (15) (16) The overlap integrals depend on: • the energy level occupied by the ions, because the distribution is different for each level • the power, because the ion dopant distribution is power dependent • the wavelength, because the optical mode profile is wavelength dependent In principle, the overlap integrals are also functions of z , due to variations in doping level along the fiber, and mode coupling (if more than one mode is supported). 550 ERBIUM DOPED FIBER For a fundamental mode approximated by a Gaussian profile and a uniformly doped fiber with doped radius b , the overlap of the mode with the total ion profile n t ( r, φ, z ) is given by: 2 Γt = 1 – e – 2b ----------2 w (17) In the low-power limit, all excited-state overlap integrals with the Gaussian approximation reduce to: 2 4b – -------2w b-2 ⎞ 1-------------------–e Γ 1, 2, 3, 4 ( P → 0 ) ≈ ⎛ --2 ⎝w ⎠ 2b --------1–e –w (18) 2 where Equation 18 is an approximated form of the upper levels (1, 2, 3 and 4). LP 01 mode approximation with a uniformly doped fiber and fiber doped radius b , the overlap with the total ion distribution is given by: For the ub ⎞ 2 [ J 2 ( ub ⁄ a ) + J 2 ( ub ⁄ a ) ] Γ t = ⎛ ------------------1 ⎝ V J ( u )⎠ 0 a 1 (19) Typically, the fiber doped radius is less than or equal to the core radius ( b ⁄ w ≤ 0.8 ), and for b ⁄ w ≤ 0.8 , the integrals also have weak power dependence [1]. For most cases, therefore, it is reasonable to assume that overlap integrals are power independent and are equal to Γ t for ions in all the energy levels. 551 ERBIUM DOPED FIBER Additional Effects Background loss Background loss in a fiber amplifier or laser is usually negligible compared to absorption coefficients and discrete losses. However, the background loss may be significant for lightly-doped fibers, for losses at the signal wavelength of a four level ion, for wavelengths far from absorption maxima, and for wavelengths beyond the low-loss region of the host glass. The actual fiber loss is composed of the Rayleigh backscattering loss, and losses from impurities. Here, the excess loss, α EL , is assumed to be wavelength-independent, and is given by: α EL = l 1310nm – α RS ( 1310nm ) where l 1310nm is the total loss at 1310nm and Rayleigh scattering effect at 1310nm. α RS ( 1310nm ) is the loss due the The user specifies the total loss at 1310 nm ( a 1310nm ), from which the component calculates the excess loss. The loss at any other wavelength then adds an additional term to the propagation equations as: + dP k + + + --------- = ( σ e ( v k ) + σa ( v k ) ) ⋅ Pk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ Pk ( z ) ⋅ n t ⋅ Γ k + σ e ( v k ) ⋅ P0k ⋅ n 2 ⋅ Γ k – ( α RS ( v k ) + α EL ) ⋅ P k dz (20) The user has the possibility of considering the excess loss as wavelength dependent. In this case, a file has to be provided that contains the total loss characteristics for the band of interest. Then, the wavelength dependent excess loss will be defined as: α EL ( v k ) = l ( v k ) – α RS ( v k ) Note: The effects of background loss are only considered during the Giles algorithm calculation. Rayleigh scattering 552 ERBIUM DOPED FIBER Rayleigh Backscattering is incorporated in the model by coupling each forward _ _ + Pk P k traveling signal at a wavelength to a backward-traveling P refk and + forward-traveling P refk signal at the same wavelength: and backward + dP + + + ---------k = ( σ e ( v k ) + σa ( v k ) ) ⋅ P k ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ Pk ( z ) ⋅ n t ⋅ Γ k + σ e ( v k ) ⋅ P 0k ⋅ n 2 ⋅ Γ k – α RS ( v k ) ⋅ P k dz (21) _ _ _ dP refk + – -------------- = ( σ e ( v k ) + σ a ( v k ) ) ⋅ Prefk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P refk ( z ) ⋅ n t ⋅ Γ k + C ⋅ α RS ( v k ) ⋅ Pk dz (22) _ _ _ _ (23) dP – --------k- = ( σ e ( v k ) + σ a ( v k ) ) ⋅ Pk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P k ( z ) ⋅ n t ⋅ Γ k + σ e ( v k ) ⋅ P 0k ⋅ n 2 ⋅ Γ k – α RS ( v k ) ⋅ P k dz + _ dP refk + + -------------- = ( σ e ( v k ) + σ a ( v k ) ) ⋅ Prefk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P refk ( z ) ⋅ n t ⋅ Γ k + C ⋅ α RS ( v k ) ⋅ Pk dz where (24) α RS ( v k ) is the background loss caused by Rayleigh scattering, and C is the backscattering capture fraction. The component has the option of loading the capture fraction from a file (wavelength dependent) or generating a theoretical capture fraction using the definition given by [2]: NA 2 1 C = ⎛⎝ --------⎞⎠ ⋅ -----n m o (25) n Where NA is the fiber numerical aperture, n o is the refractive index of the fiber and m n depends on the refractive index profile. For single mode fibers a typical value for m n is 4.55. The Rayleigh background loss α RS ( v k ) in a fiber is given by [3]: 1000nm α RS ( v k ) = ( 0.63 + K R Δn ) ⎛⎝ --------------------⎞⎠ λ ( nm ) 4 (26) The first term (0.63 dB/km) is the scattering loss for pure silica fiber at 1000 nm, and the second term accounts for the material and geometrical dependence. The Raleigh constant parameter, K R , generally is equal to about 70 dB/km for Ge co-doped fiber, 553 ERBIUM DOPED FIBER and about 150 dB/km for Aluminum co-doped fiber. The index difference derived from the numerical aperture, Δn can be NA , as: 2 NA Δn = ---------------∗ 2 1.45 where it is assumed that the fiber refractive index is approximately 1.45. In accordance with Equation 20 - Equation 23, the equation that gives the density population in the metastable level, Equation 10, was modified to take into account the reflected powers in the n 2 calculation for the steady state case. Double Rayleigh scattering Double Rayleigh scattering occurs when a portion of the backscattered signal is reflected again and it is recoupled to the forward direction. It is a problem because it creates paths of different lengths for signals to travel. It is considered in the model changing Equation 22 and Equation 24 by: _ _ _ dPrefk + + – -------------- = ( σ e ( v k ) + σ a ( v k ) ) ⋅ Prefk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P refk ( z ) ⋅ n t ⋅ Γ k + C ⋅ α RS ( v k ) ⋅ ( P k + P refk ) dz + _ _ dPrefk + + -------------- = ( σ e ( v k ) + σa ( v k ) ) ⋅ P refk ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ Prefk ( z ) ⋅ n t ⋅ Γ k + C ⋅ α RS ( v k ) ⋅ ( P k + Prefk ) dz (27) (28) The buildup of backscattered light is always included in the Giles calculation, but it can be neglected by setting the capture fraction to zero or not including the Rayleigh scattering in the simulation. The degradation of EDFA performance from internal backscattering has been reported in [3] and [4]. 554 ERBIUM DOPED FIBER Er3+ - Er3+ Interaction The Erbium Doped Fiber Amplifier component allows the user to consider interactions between neighboring ions. The exchange of energy between neighboring ions is also known as "Concentration Quenching". The most important ion-ion interaction for EDFA is the stepwise up-conversion shown in Figure 2. Initially, there are two ions at the metastable level. Energy is transferred from the donor ion, which falls back to the ground level, and the acceptor ion, which returns to the metastable level by phonon transitions, after being excited to one of the upper levels. The net result is that two excited ions become one excited ion so that the quantum efficiency is reduced. Therefore, it has a negative impact on amplifiers. Figure 2 Stepwise up-conversion Stepwise up-conversion becomes stronger as the distance between the doped ions decreases, i.e. as the concentration increases. Depending on the fiber material, it becomes significant when the concentration is greater than about 1000 ppm. There are three models to account for stepwise up-conversion. Homogeneous upconversion Considering that the ions are independent, i. e., if one ion is excited to the I 13 ⁄ 2 state this would not prevent a neighboring ion from also being excited to the I 13 ⁄ 2 state. The upconversion fluorescence intensity can be calculated redefining Equation 1 as [5]: dn 2 ( r, φ, z, t ) ------------------------------- = dt σa ( vk ) σe ( vk ) - ⋅ i k ⋅ Pk ( z ) ⋅ n 1 ( r, φ, z ) – ---------------- ⋅ i k ⋅ Pk ( z ) ⋅ n 2 ( r, φ, z ) _ ∑ --------------hvk hv k (29) k n 2 ( r, φ, z, t ) – ---------------------------- – ( 1 + 1 ⁄ m ) ⋅ U e ⋅ n 2 ( r, φ, z, t ) τ 555 ERBIUM DOPED FIBER m is the branching ration between the I 11 ⁄ 2 - I 15 ⁄ 2 transition (980nm) and the I 11 ⁄ 2 - I 13 ⁄ 2 nonradiative transition; U c is the two-particle upconversion coefficient ( U c is concentration independent). In [7], the value found for the m and 3 U c parameters were 1e4 and 1e-22 ( m ⁄ s ), respectively. Considering the steadyWhere state case, the rate equation (29) becomes: σa ( vk ) - ⋅ i k ⋅ Pk ( z ) ⋅ n t ( r, φ, z ) ∑ --------------hv k k n 2 ( r, φ, z, t ) = -------------------------------------------------------------------------------------------------------------------------------------------------------------σa ( vk ) + σe ( vk ) 1---------------------------------------⋅ i ⋅ P ( z ) + ( 1 + 1 ⁄ m ) U ⋅ n ( r , φ , z , t ) ⋅ + k k c 2 ∑ hv k τ k (30) Inhomogeneous pair induced quenching In this model [6] [7], erbium ions exist as two distinct species: single ions (no interaction with others) and clustered ions. The ions residing in each cluster can occupy only two energy levels: State 1 - all the ions in the ground state or State 2 - only one ion per cluster in the excited state. When more than one ion is excited in the cluster, the excitation energy is rapidly transferred from one ion to another, and the upconversion continues until all but one ion in the cluster occupies the metastable excited-state. Note: It is assumed that all the clusters are of the same size and contain the same number of ions, m k . For the total concentration of erbium ions, introduced as n t , the concentration of clustered ions is n c = m k ⋅ k ⋅ n t , where k is the relative number of clusters and m k ⋅ k is the percentage of ions in clusters. The concentration of single ions is n s = ( l – m k ⋅ k ) ⋅ nt . 556 ERBIUM DOPED FIBER For single ions the rate equations is: dn 2S ---------- = dt σa ( vk ) σe ( vk ) 1 - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 1S ( r, φ, z ) – ∑ ---------------- ⋅ ik ( r, φ ) ⋅ Pk ( z ) ⋅ n 2S ( r, φ, z ) – --- ⋅ n 2S ( r, φ, z ) ∑ --------------hv k hv k τ k (31) k (32) n 1S + n 2S = 1 – ( m k ⋅ k ) ⋅ n t For the steady-state case: σa ( v k ) - ⋅ i k ( r, φ ) ⋅ Pk ( z ) ⋅ ( 1 – m k ⋅ k ) ⋅ n t ∑ --------------hv k (33) k n 2S ( r, φ, z ) = -------------------------------------------------------------------------------------------------------σa ( vk ) + σe ( vk ) 1--+ -------------------------------------⋅ i ( r , φ ) ⋅ P ( z ) k k ∑ τ hv k k For clustered ions, the rate equation is: dn 2C ------------ = dt σa ( vk ) σe ( v k ) 1 - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ ( m k ⋅ k ⋅ n t – m k ⋅ n 2C ) – ∑ ---------------- ⋅ i k ( r, φ ) ⋅ Pk ( z ) ⋅ n 2C ( r, φ, z ) – --- ⋅ n 2C ( r, φ, z ) ∑ --------------hv k hv k τ k k σa ( vk ) - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ m k ⋅ k ⋅ n t ∑ --------------hv k k n 2C ( r, φ, z ) = ---------------------------------------------------------------------------------------------------------------------------------------------------------------σe ( vk ) σa ( v k ) --------------⋅ i ( r , φ ) ⋅ P ( z ) + --------------⋅ i ( r , φ ) ⋅ P ( z ) ⋅ m ⋅ k ⋅ n k k k t ∑ hvk k ∑ hvk k k k (34) Then, the ion population in the metastable level is: σa ( vk ) - ⋅ ik ( r, φ ) ⋅ Pk ( z ) ⋅ ( 1 – m k ⋅ k ) ⋅ n t ∑ --------------hv k k n 2 ( r, φ, z, t ) = n 2S ( r, φ, z, t ) + n 2C ( r, φ, z, t ) = -----------------------------------------------------------------------------------------------------+ σ a ( v k ) + σe ( v k ) 1 ⋅ ik ( r, φ ) ⋅ Pk ( z ) + --∑ -------------------------------------hv k τ k σa ( vk ) - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ ( 1 – m k ⋅ k ) ⋅ n t ∑ --------------hv k k + ---------------------------------------------------------------------------------------------------------------------------------------------------------σe ( vk ) σa ( vk ) 1 - ⋅ i k ( r, φ ) ⋅ Pk ( z ) + ∑ --------------- ⋅ ik ( r, φ ) ⋅ P k ( z ) ⋅ m k + --∑ --------------hv hv τ k k k k 557 (35) ERBIUM DOPED FIBER Homogeneous Upconversion and Inhomogeneous Pair Induced Quenching This case is a combination of the cooperative upconversion and the pair induced upconversion. The combined model is similar to the inhomogeneous model, except that the single ions experience concentration quenching at the same rate as for the homogeneous model. Therefore, the population inversion in the steady-state becomes: N 2 ( r, φ, z, t ) = N 2S ( r, φ, z, t ) + Nn 2C ( r, φ, z, t ) σa ( vk ) - ⋅ i k ⋅ Pk ( z ) ⋅ ( 1 – m k ⋅ k ) ⋅ n t ( r, φ, z ) ∑ --------------hv k k N 2 ( r, φ, z, t ) = -----------------------------------------------------------------------------------------------------------+ σa ( vk ) + σe ( v k ) 1 ⋅ i k ( r, φ ) ⋅ Pk ( z ) + --∑ -------------------------------------hv k τ k (36) σa ( vk ) - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ m k ⋅ k ⋅ n t ∑ --------------hvk k + ---------------------------------------------------------------------------------------------------------------------------------------------------------σa ( vk ) σa ( vk ) 1 --------------i ( r , φ ) P ( z ) --------------i ( r , φ ) P ( z ) m ⋅ ⋅ + ⋅ ⋅ ⋅ + -k k k ∑ hvk k ∑ hv k k τ k k The first term on the right-hand side is for single ions and the second term is for clustered ions. Temperature dependence The temperature dependence exhibited by an erbium doped fiber is mainly attributed to the variation in the occupation probability density of each manifold with temperature. In an EDFA, the gain is temperature dependent through the temperature dependence of the gain and absorption coefficients. Therefore, to represent the temperature dependence of an EDFA, the model needs properly represent the temperature dependence of g ( λ ) and α ( λ ) (or σ e ( λ ) and σ a ( λ ) ). The temperature model in the erbium doped fiber amplifier component is based on physical intuition and use fitting parameters to generate modeling parameters at any temperature. It is assumed that the temperature dependence of an EDF is due to the variation in the occupation probability density. Using the Boltzmann's law for the level occupation and the definition that the sum of all occupation probabilities for all states of the manifold must equal unit, integral expressions for g ( λ ) and α ( λ ) were derived [8]. After a series of approximations, the following equations [8], outline an effective procedure for calculation of the temperature dependence of absorption and emission coefficients: α ( λ, T ) = α ( λ, ∞ ) ⋅ e 558 βa ( λ ) ⎞ ⎛ ------------⎝ KT - ⎠ (37) ERBIUM DOPED FIBER g ( λ, T ) = g ( λ, ∞ ) ⋅ e βe ( λ ) ⎞ ⎛ ------------⎝ KT ⎠ (38) K is the Boltzmann's constant, and T is the temperature in degrees Kelvin. The fitting parameters α ( λ, ∞ ) and g ( λ, ∞ ) are both temperature independent where and can be interpreted as the absorption and gain at "infinite" temperature when all energy levels of each manifolds are equally occupied, according with to Boltzmann statistics. However, a more appropriate interpretation of α ( λ, ∞ ) and g ( λ, ∞ ) is that they represent the absorption and gain coefficient when all levels of the relevant manifolds are uniformly occupied. The parameters β a ( λ ) and β e ( λ ) are expected to capture the thermal occupation probability of the initial energy level for the transition at a given wavelength. α ( λ, ∞ ) , g ( λ, ∞ ) , β a ( λ ) , and β e ( λ ) , the component requires two sets of measurement data for g ( λ ) and α ( λ ) at different temperatures. One set of measured g ( λ ) and α ( λ ) for "infinite" temperature is provided by the component. Another set of measured data for g ( λ ) and α ( λ ) (or σ e ( λ ) and σ a ( λ ) ) at a different temperature has to be provided by the user. With these two sets of data for g ( λ ) and α ( λ ) at different temperatures, the component is able to calculate the functions β a ( λ ) and β e ( λ ) . The values of g ( λ ) and α ( λ ) , In order to calculate functions at an arbitrary temperature defined by the user, will then be generated by the component in accordance to Equation 37 and Equation 38. Note that the set of measured data for the gain and absorption coefficients at "infinite" temperature, α ( λ, ∞ ) and g ( λ, ∞ ) , provided by the component, are expected to represent accurately the dependence of EDF spectra for fibers with similar compositions only. However, in [9] is reported that only minor differences for a variety of silica-based, aluminum-codoped EDFs with a wide range of germanium and aluminum levels were observed [9][8]. More information about how temperature dependence can be simulated can be found in the tutorials. 559 ERBIUM DOPED FIBER Figure 3 Absorption α ( λ, ∞ ) and gain g ( λ, ∞ ) coefficients at infinite "temperature" Excited-State Absorption Effect (ESA) The excited-state absorption can affect amplifiers in two ways; through parasitic absorption of pump photons, or signal photons. With pump ESA, the pump light at frequency v p is not absorbed from the ground level (1) of the rare earth ion, but from an excited level (2), due to the existence of a third level (3) whose energy gap ΔE = E 3 – E 2 with level (2) happens to closely match the pump photon energy h ⋅ v p . This happens only if the ESA cross section overlaps with the ground state absorption (pump absorption cross-section). In the case of signal ESA, the signal light h ⋅ v s is absorbed from the metastable level (2) to a level (3), due to the same energy gap matching relation ΔE = E 3 – ( E 2 ≈ hv s ) . This indicates that of energy both pump and signal ESA result in an excess loss for the pump or the signal. The ESA effect has been observed to occur in Er-doped fibers in several wavelength bands, but our main interest is in the 980 nm pumping band and in 1500-1620 nm signal band. In the first band, the pump ESA initiated from the metastable level 4 I13 ⁄ 2 , is nonexistent near 980 nm [10]. However, pump ESA can be initiated from 4 4 the energy short-lived I11 ⁄ 2 level; where the terminal level is F7 ⁄ 2 . Nevertheless, since the level population is rapidly damped by nonradiative decay, ESA from this level can occur only at high pump power levels [10]. Therefore, the ESA effect in the second band can be more serious in the degradation of amplifier performance, mainly in L-band amplifiers (see lesson about ESA in the tutorials) and it is taken into consideration in the Erbium doped fiber modeling. 560 ERBIUM DOPED FIBER To include the ESA effect in our two-level model, Equation 8 was modified to introduce the ESA cross-section σ ESA : dP ---------k = ( σ e ( v k ) + σESA ( v k ) + σ a ( v k ) ) ⋅ P k ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P k ( z ) ⋅ n t ⋅ Γ k + P 0k ⋅ σ a ( v k ) ⋅ n 2 ⋅ Γ k dz (39) Additional information about the modeling of the ESA effect can be found in [10]. Figure 4 ESA Cross-sections Inhomogeneous broadening The previous model considered only homogeneous broadening, which is satisfactory to predict the gain and noise performance of a majority of erbium doped fiber amplifiers. However, to accurately describe the saturation behavior of the amplifier and the effect of spectral-hole burning, inhomogeneous broadening has to be considered. The main assumption in the modeling of this effect is that the variation of the stark splitting from site to site due to the change of the ligand fields leads to randomization of central frequencies of the transition lines; the linewidths, the absorption and emission cross-sections, and the fluorescence lifetime do not change. The density distribution for inhomogeneous broadening of central frequencies of the transition lines is given for a Gaussian function: f(ω) = ω ⎞2 4--------------------⋅ 1n ( 2 -) ⋅ exp – 4 ⋅ 1n ( 2 ) ⋅ ⎛ -------⎝ Δω ⎠ 2 i π ⋅ Δω i (40) 2 Δω i = 2 ⋅ π ⋅ c ⋅ Δλ inh ⁄ λ is the inhomogeneous broadening spectral bandwidth and Δλ inh is the inhomogeneous line width. where 561 ERBIUM DOPED FIBER The observed (measured) inhomogeneous absorption and emission cross-sections, I I σ a ( v ) and σ e ( v ) , are the convolutions of the homogeneous absorption and H H emission cross-sections, σ a ( v ) and σ e ( v ) , with the normalized inhomogeneous broadening distribution f ( v ) , and can be expressed by: I σe( v ) ∞ = H ∫ f ( v – v' ) ⋅ σe ( v ) ⋅ dv' (41)a –∞ I σa ( v ) ∞ = H ∫ f ( v – v' ) ⋅ σa ( v ) ⋅ dv' (41)b –∞ The description of the inhomogeneous broadening is based on the following form of the propagation equation suggested in [10]: dP ( ω k ) ----------------- = ρ ⋅ Γ k ⋅ P ( ωk ) ⋅ dz ∞ ∫ dω ⋅ f ( ω ) –∞ H ⋅ σa ( ωk – ω) ⋅ H σe ( ωk – ω ) ---------------------------H σa ( ωk – ω ) Pm ⋅ H (ω – ω) ⋅ τ ∑ ---------------------σ h ⋅ v ⋅ Am a m m ------------------------------------------------------------------------------------------------------------------------- Pm H H 1 + ∑ --------------------⋅ ( σa ( ωm – ω ) + σe ( ωm – ω ) ) ⋅ τ h ⋅ v ⋅ A m m _ (42) Pm H ⎛1 + ⎞ ---------------------σ e ( ω m – ω ) ⋅ τ⎠ ∑ ⎝ h ⋅ v ⋅ A H m m – ρ ⋅ Γ k ⋅ P ( ω k ) ⋅ ∫ dω ⋅ f ( ω ) ⋅ σ a ( ω k – ω ) ⋅ ------------------------------------------------------------------------------------------------------------------------Pm H H 1 + ∑ --------------------- ⋅ ( σ a ( ω m – ω ) + σe ( ω m – ω ) ) ⋅ τ –∞ h ⋅ v ⋅ Am m ∞ To include spontaneous emission, a noise source term is introduced in Equation 42. In order to determine the homogeneous absorption and emission cross-section used in the propagation equation, a deconvolution procedure to resolve Equation 41 is applied. In Homogeneous cross-sections, there is a description of the procedures used in the component to generate the homogeneous cross-sections. Homogeneous cross-sections Homogeneous cross-sections can be derived from the experimental (inhomogeneous) cross-sections through an inversion Fourier transformation in Equation 41, (a) and (b). However, a direct deconvolution of Equation 41 has a unique solution only when the functions I I σ a ( λ ) , σ e ( λ ) and their evanescent tails are well defined analytically. This is not the case with experimental line shapes. 562 ERBIUM DOPED FIBER Nevertheless, there is a possibility of fitting the line shapes with a superposition of Gaussian functions such as nG 2 ⎛ ⎛ ( λ – λi ) ⎞ ⎞ I ( λ ) = ∑ a i ⋅ exp ⎜ – 4 ⋅ 1n ⎜ ( 2 ) ⋅ --------------------⎟ ⎟ 2 ⎝ ⎝ ⎠⎠ Δλ i i a i , λ i , and Δλ i are the Gaussian line shapes parameters for the fitting. The parameter n G is the number of Gaussians. where Using this superposition of Gaussian functions; the deconvolution of Equation 41 can be calculated analytically. With the Gaussian functions line shapes parameters found in the numerical fitting, the homogeneous emission and absorption cross-sections can calculated in accordance with the inhomogeneous line width ( Δλ inh ) provided by the user using the definition [10]: H σ a, e ( λ ) nG = ∑ i a, e ai 2 ⎛ Δλ i ( λ – λi ) ⎞ ⋅ --------------------------------⋅ exp ⎜ – 4 ⋅ 1n ( 2 ) ⋅ --------------------⎟ 2 2 2 ⎝ ⎠ Δλ Δλ i – Δλ inh i (43) The Erbium-doped fiber component is able to do the fitting of the cross-sections provided by the user using the number of Gaussian functions ( n G ) determined by the Number of Gaussians parameter. Figure 5 Homogeneous (a) absorption and (b) emission cross-sections 563 ERBIUM DOPED FIBER Approximations of Giles-Desurvire rate and propagation equations Saleh model The Saleh model is an approximation of the propagation and rate equations for a twolevel system in the steady-state case. This allows for an analytical solution of the equations by means of a transcendental equation, instead of N coupled differential equations [11]. This model could be successfully applied to the study of the small signal gain and saturated gain, optimum fiber length, and saturated power. The theory uses some simplifying assumptions. First, although spontaneous decay is accounted for, amplified spontaneous emission (ASE) is neglected. This is valid for fiber lasers above threshold and for fiber amplifiers when the input signal power is significantly above the equivalent ASE noise input power, as discussed in [11]. Second, it is assumed that there is no excited state absorption (ESA) at any of the pump or signal wavelengths. Third, it is assumed that field and ion distributions are independent of fiber position and power levels. These assumptions are satisfactory in the case of typical doped fibers that have a doped fiber radius less than the core fiber radius. Background loss is also neglected, as with three level ions such as erbium, the absorption by the rare earth ions is typically much greater than other losses. Using the assumptions, Equation 8 could be integrated analytically from 0 to L [11]. The result is given by the following expression for the output photon flux out Qk where out Qk in Qk : ( α k + gk ) ⎧ in in out ⎫ = Q k exp ⎨ – α k L + --------------------- ⋅ ( Q tot – Q tot ) ⎬ ζ ⎩ ⎭ (44) out = P k ⁄ ( hv k ) is the output photon flux for kth signal, in Q k = P k ⁄ ( hv k ) is the input photon flux for kth signal out Q tot = out ∑ Qk is the total output photon flux k in Q tot = in ∑ Qk is the total input photon flux. k Summing Equation 44 over all k signals yields: out Q tot = in ⎧ ( αk + g k ) in out ⎫ - ⋅ ( Q tot – Q tot ) ⎬ ∑ Qk exp ⎨⎩ – αk L + --------------------ζ ⎭ (45) k which is a implicit equation for the total output photon flux out out Q tot . Note that Q tot is completely determined, given the input flux, by the following four fiber parameters; out α k, g k, ζ, and L (fiber length). Solving Equation 45 for Q tot allows for the determination of the output fluxes of each individual signal through Equation 44. 564 ERBIUM DOPED FIBER Since the Saleh model neglects ASE, it becomes less accurate for cases in which ASE becomes significant, e.g. for low input powers (less than about -20 dBm, depending on the gain and signal wavelengths). In these cases, the accuracy is improved by using an equivalent ASE input, which inputs effective input beams at both ends of the fiber with equivalent input powers: in hv k P k = 2n sp ( v, z in )Δv hv k (46) where z in = 0 for the forward ASE, and z in = L for the backward ASE. Δv is the spectral width of the noise beams. The spontaneous emission factor is given by: n 2 ( z in ) n sp ( v, z in ) = --------------------------------------- ⋅ ε(v) n 2 ( z in ) – n 1 ( z in ) where (47) ε ( v ) = σ a ⁄ σ e is the ratio of cross-sections. The Saleh model has the advantage that longitudinal integrations are not required, so it is much faster to solve. Note that unlike literature that typically uses one or two equivalent ASE beams centered at the spectral peaks near 1532 nm and 1555 nm, this component has an equivalent ASE beam for each of the bins defined in the Noise tab. Jopson model The Saleh model only estimates the pump and signal powers, and equivalent ASE at the doped fiber output. These values are used to estimate the population inversion at the doped fiber ends. However, no information is obtained about the values along the fiber. Jopson and Saleh extended the Saleh model to obtain estimates of the powers and inversion levels along the fiber [12]. The photon flux Q k in distance z can be determined by: ( αk + gk ) ⎧ ⎫ Q k ( z ) = Q k ( 0 ) exp ⎨ – u k α k z + u k --------------------- ⋅ (Q(0) – Q( z) ) ⎬ ζ ⎩ ⎭ (48) where Q ( z ) is defined by: Q( z) = ∑ uk Qk ( z ) (49) k and it is computed from the transcendental equation: Q(z) = ∑ uk Qk ( z ) e –uk αk a u k (50) e [ ( Q ( 0 ) – Q ( z ) ) ⋅ ( αk + gk ) ⁄ ζ ] 565 ERBIUM DOPED FIBER In order to obtain the pump, signals, and equivalent ASE powers and population inversion along the fiber, starting from either end of the fiber, this equation can be solved for in every user-defined step. Noise λ k , of a single polarization, emitted in a single direction by a section of amplifier of length dz is given by: dP = g k ⋅ n2 ( z ) ⋅ Δv ⋅ dz The spontaneous-emission noise at wavelength where n 2 ( z ) can be determined using Equation 50 and Equation 7. The amplified spontaneous emission noise (ASE) emitted from the output or input end λ k can be obtained by multiplying the spontaneous emission from each section of the amplifier by the amplifier gain at λ k from that of the amplifier at wavelength section to the desired end of the amplifier. The gain is given by: G k ( 0, z ) = e – uk αk z uk e [ ( Q ( 0 ) – Q ( z ) ) ⋅ ( α k + g k ) ⁄ ζ ] , where G k ( 0, z ) is the gain from the input ( z = 0 ) to the length z and G k ( z, L ) = e –u k αk ( L – z ) u k e [ ( Q ( z ) – Q ( L ) ) ⋅ ( α k + g k ) ⁄ ζ ] , where G k ( z, L ) is the gain from the length z to the output L . 566 ERBIUM DOPED FIBER Additional input parameters Most of the input parameters for the component were described in the sections before and they can be easily linked to a particular effect or equation. However, there are several parameters that have not been described yet, or they are loaded from files. Main tab This tab contains the basic parameters of the Erbium-doped fiber. All of them are well described in the technical description. However, there is a new parameter (Input data parameter) that gives the user the choice to enter the saturation parameter or to enter the fiber parameters (core radius, doped radius, numerical aperture, and erbium density population). Cross-sections tab In this tab the user defines which cross-section file has to be loaded and what characteristics it has. There are two options available to prepare the cross-section file, which is specified in an ASCII file. The first option is to provide directly the crosssection in an input file with three columns. The first column refers to the wavelength (or frequency) in [m], [nm], [Hz] or [THz] units; the File frequency unit parameter defines the unit of this column. The second column gives the absorption cross-section in [m2] units. The third column gives the emission cross-section file in [m2] units. The unit of the second and third column must be in [m2]. As an example, one possible cross-section file format is: λ λ [ nm ] (nm) 2 2 σa [ m ] σe [ m ] 975 1.95386E-25 0 976 2.07791E-25 0 977 2.20195E-25 0 978 2.26852E-25 0 979 2.13394E-25 0 980 1.99935E-25 0 981 1.86477E-25 0 982 1.73019E-25 0 983 1.5956E-25 0 1450 5.88956E-26 1.78862E-26 1451 6.19338E-26 1.87881E-26 1452 6.50958E-26 1.97301E-26 1453 6.83832E-26 2.06921E-26 : : 567 ERBIUM DOPED FIBER λ λ [ nm ] (nm) 2 2 σa [ m ] σe [ m ] 1454 7.17971E-26 2.16742E-26 1455 7.53386E-26 2.26767E-26 1456 7.90081E-26 2.37003E-26 1457 8.2806E-26 2.4746E-26 1458 8.67324E-26 2.58149E-26 1459 9.07873E-26 2.69085E-26 : The second option is to provide the absorption and gain coefficients (or Giles parameters) as input parameters that are converted to cross-section by internal routines in the software. The file format in this case contains three columns. The first column refers to the wavelength (or frequency) in [m], [nm], [Hz] or [THz] units; the File frequency unit parameter defines the unit of this column. The second column gives the absorption coefficient in [dB/m] units. The third column gives the emission coefficient in [dB/m] units. The unit of the second and third column must be in [dB/m]. An example of this input file is: λ λ [ nm ] (nm) α [ dB ⁄ m ] g∗ [ dB ⁄ m ] 977 5 0 978 5 0 979 5 0 980 5 0 981 5 0 1460 1.357 0.29 1461 1.417 0.309 1462 1.464 0.328 1463 1.525 0.35 1464 1.562 0.365 1465 1.562 0.387 1466 1.562 0.411 : : : When the EDF component load the cross-section file, it detects whether the file contain the Giles parameters ( g ( λ ) and ( σ a ( v k ) and 568 σ e ( v k ) ). α ( λ ) ) or cross-section parameters ERBIUM DOPED FIBER The parameter OptiAmplifier format is used to allow the component load crosssections files originated from the software OptiAmplier. Therefore, if the user wants to load a cross-section under the crs format (format used in the OptiAmplifier software), the OptiAmplifier format parameter has to be set TRUE. Enhanced tab The enhanced tab defines the parameters related to the background loss, Rayleigh scattering, Er +3 – Er +3 interaction effects, ESA, and temperature dependence. First, the user can choose the Background loss data type parameter that determines the background loss through the loss at 1310nm (Loss at 1310 nm parameter) or using a wavelength dependent background loss loaded from a file. In the second case, the user has to specify the name of the file contained the losses in the Background loss file name parameter. The format of this file must be similar to the following example: λ λ [ nm ] (nm) α [ dB ⁄ km ] 1460 10 1461 10.5 1462 10.2 1463 10.1 1464 10.3 The user can include the Rayleigh scattering effect or not in the simulations through the parameter Include Rayleigh scattering. If the Include Rayleigh scattering parameter is TRUE, then the user has to specify the value of the Rayleigh constant. The Backscattering capture parameter determines if the component will generate the capture fraction using Equation 25, or the user will provide a file with the capture fraction - in this case the user should specify the file name in the Rayleigh capture file name parameter and the file has to be in the format similar to the below: λ λ [ nm ] (nm) C [ dB ] 1460 -20 1461 -21.5 1462 -21 1463 -20.5 1464 -20.48 In the case of Er +3 – Er +3 interaction effects, the user has to decide to include or not this effect through the parameter Include ion-ion interaction effects. If the user chooses to include this effect, the parameter Ion-Ion interaction effect has to specify 569 ERBIUM DOPED FIBER which Er +3 – Er +3 interaction effect will be considered in the simulations; Homogeneous upconversion, pair-induced quenching, or a combination of both. When the ion-ion effect is defined, then the parameters necessaries for that effect will be enabled. Upconversion coefficient, ions per cluster, and relative number of clusters are the parameters that have to be specified depending on the effect considered. The user can include the temperature dependence in EDF model setting the parameter Include temperature dependence to TRUE. After this, the user has to define in which temperature, the cross-section defined in the cross-sections tab, was measured (Cross-section temperature parameter). With these parameters and the cross-section at infinite temperature stored in the component, it is possible to calculate the parameters β a ( λ ) and β e ( λ ) from Equation 37 and Equation 38. The other parameter to be defined is the temperature that will be considered in the simulation (Temperature parameter). For more information, refer to the tutorial about temperature dependence. The ESA effect can be included in the EDF simulation. In this case the user has to set the parameter Include ESA effect to TRUE. After this, the user has to provide the ESA cross-section. Similar to the cross-sections in the cross-section tab, the ESA crosssection can be in the Giles format [ dB 2 ⁄ m ] or cross-section format [ m ]. The difference is the ESA cross-section file must have only two columns: (1) wavelength (or frequency) in [m], [nm], [Hz] or [THz] units and (2) the ESA cross-section. The unit of the wavelength column has to be the same as defined in the File frequency unit parameter (Cross-sections tab). The last parameter is Extract ESA from emission. If this parameter is TRUE, it means that the second column of the ESA file contains the ESA cross-section and the emission cross-section together, so the component has to extract the ESA crosssection from this file. If the Extract ESA from emission parameter is FALSE, the component assumes that the second column contains only the ESA cross-section. An example of ESA file is: λ λ [ nm ] (nm) g∗ [ dB ⁄ m ] 1449.91984 0.32257 1451.30261 0.35195 1452.68537 0.38317 1454.06814 0.4175 1455.4509 0.4571 : 570 ERBIUM DOPED FIBER λ λ [ nm ] (nm) g∗ [ dB ⁄ m ] 1571.60321 4.08152 1572.98597 3.81553 1574.36874 3.60032 1575.7515 3.37804 1577.13427 3.20419 1578.51703 3.05017 : 1648.98 1.43477 1649.23 1.4325 1649.48 1.49899 1649.73 1.42809 1649.98 1.42593 1650.23 1.49333 For more information, refer to the tutorial about ESA. Numerical tab The numerical tab contains most of the options related to the different models or approximations used in the EDF model. In the Calculation algorithm parameter, the user can choose between the four possible models: (1) Saleh, (2) Jopson, (3) Giles, and (4) Inhomogeneous. These four possible models are described in the technical background. If a model is selected, for example the model number 3 (Giles model), the EDF component will start the simulation process from the first model (Saleh) until the model chose by the user (Giles model). Figure 6 details how the component works. 571 ERBIUM DOPED FIBER Figure 6 Diagram describing the process order of the algorithm models The EDF component's preprocessing is done to improve the speed of convergence in the model selected by the user. This preprocessing is done in accordance with the complexity of each model. The user defines the parameter Relative error that indicates the threshold value which the component uses to decide if the results from the iterative process have converged. Another parameter is the Max. number of iterations. This parameter defines the maximum number of iterations allowed for the numerical method to reach the value determined by the Relative error parameter. The parameter Number of longitudinal steps defines the minimum number of steps in the fiber to be considered in the Jopson, Giles, and inhomogeneous method. If the Inhomogeneous algorithm is chose, then the user has to specify the parameter Inhomogeneous accuracy. This parameter determines the tolerance of the numerical integration of Equation 42, and directly influences the simulation time. Some simulations have shown us that this parameter should be between 0.01 and 0.001 to obtain accurate results in a reasonable time. The user can make their selection via the Overlap factor data parameter, by determining if the component will calculate the overlap integral or the component or load the overlap factor from a file. For the calculation case, the Geometrical model parameter has to be defined. The Geometrical model parameter indicates if the 572 ERBIUM DOPED FIBER component will use one of the Gaussian approximations (Equation 13 - Equation 16) or the LP01 mode to calculate the overlap integral. Another possible method to calculate the overlap integral is to consider the power dependence on it. The Overlap factor parameter determines if the power dependence has to be taken into consideration. In this case, Equation 6 is solved numerically for the LP01 mode and the number of integrations to be done in the fiber is defined by the Nr. of transverse integration parameter. In the other way, the confinement factor is calculated in accordance with the Geometrical model parameter. If the overlap factor is loaded from a file, the user has to specify the file name in the Overlap factor file name parameter, and the file has to be the same as the format below: λ λ [ nm ] (nm) Γ 1449.91984 0.45 1451.30261 0.44 1452.68537 0.43 1454.06814 0.42 1455.4509 0.41 If the Inhomogeneous algorithm is chose, then the homogeneous absorption and emission cross-sections are necessary for the inhomogeneous broadening model. In this case, the component generates the homogeneous cross-sections from the measured cross-sections, as explained in the technical background. For this purpose, the user has to specify the number of Gaussians to be used in the fitting and the value of the inhomogeneous linewidth. 573 ERBIUM DOPED FIBER References [1] C. Randy Giles, and Emmanuel Desurvire, "Modeling Erbium-Doped Fiber Amplifiers". IEEE Journal of Lightwave Technology, Volume: 9 Issue: 2, Feb. 1991, Page(s): 271 - 283. [2] Fiber Optic Test and Measurement, Edited by Dennis Derickson, 1997. [3] S. L. Hansen, K. Dybdal, and C. C. Larsen. "Gain Limited in Erbium-Doped Fiber Amplifiers Due to Internal Rayleigh Backscattering". IEEE Photonics Technology Letters, Volume 4, Issue 6, Jun. 1992. [4] P. F. Wysocki, G. Jacobovitz-Veselka, D. S. Gasper, S. Kosinski, J. Costelloe, and S. W. Granlund. "Modeling, Measurement, and a Simple Analytic Approximation for the Return Loss of Erbium-Doped Fiber Amplifiers". IEEE Photonics Technology Letters, Volume: 7, Issue: 12, Dec. 1995. [5] P. Blixt, J. Nilsson, T. Carlnas, and B. Jaskorzynska. "Concentration-Dependent Upconversion in Er3+-Doped Fiber Amplifiers: Experiments and Modeling". IEEE Photonics Technology Letters, Volume: 3 Issue: 11, Nov. 1991. [6] P. Myslink, D. Nguyen, and J. Chrostowski. "Effects of Concentration on the Performance of Erbium-Doped Fiber Amplifiers". Journal of Lightwave Technology, volume 15, Issue 1, Jan. 1997. [7] Blixt, P.; Jaskorzynska, B.; Nilsson, J. "Performance reduction and design modification of erbium-doped fiber amplifiers resulting from pair-induced quenching". IEEE Photonics Technology Letters , Volume: 5 Issue: 12 , Dec 1993. [8] M. Bolshtyansky, P. F. Wysocki, N. Conti. "Model of Temperature Dependence for Gain Shape of Erbium-Doped Fiber". Journal of Lightwave Technology, volume 18, Issue 11, Dec 2000. [9] P. F. Wysocki, N. Conti, and D. Holcomb. "Simple Modeling Approach for the Temperature Dependence of the Gain of Erbium-Doped Fiber Amplifiers". SPIE Conference on Optical Devices for Fiber Communication, Volume 3847, 1999. [10] Emmanuel Desurvire. "Erbium-Doped Fiber Amplifier: Principles and Applications", John Wiley & Sons. [11] A. A. M. Saleh, R. M. Jopson, J. D. Evankow, and J. Aspell. "Modeling of Gain in Erbium-Doped Fiber Amplifiers". IEEE Photonics Technology Letters, Volume: 2 Issue: 10, Oct. 1990, Page(s): 714 - 717. [12] R. M. Jopson, A. A. M Saleh. "Modeling of Gain and Noise in Erbium-Doped Fiber Amplifiers". Fiber Laser Sources and Amplifiers, SPIE Volume: 1581, 1991, Page(s): 114 - 119. [13] C. R. Giles, C. A. Burrus, D. J. DiGiovanni, N. K. Dutta, and G. Raybon. "Characterization of Erbium-Doped Fibers and Application to Modeling 980 nm and 1480 nm Pumped Amplifiers". IEEE Photonics Technology Letters, Volume: 3 Issue: 4, Apr. 1991, Page(s): 363 -365. [14] "Rare-Earth-Doped Fiber Laser and Amplifiers", Edited by M. J. F. Digonnet, 2001. [15] P. C. Becker, N. A. Olsson, and J. R. Simpson. "Erbium-Doped Fiber Amplifiers: Fundamentals and Technology". Optics and Photonics, 1999. 574 ER-YB CODOPED FIBER Er-Yb Codoped Fiber This component simulates a bidirectional Erbium-Ytterbium codoped fiber. The component solves numerically the rate and propagation equations for the steadystate case and can take into account nonlinear phase changes caused by SPM and XPM effects by propagating the signal using the nonlinear Schrödinger equation. Ports Name and description Port type Signal type Input1 Input Optical Output1 Output Optical Input2 Input Optical Output2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 1 m — [0,1000000] 2 μm — [1,1e100] 2 μm — [1,1e100] 0.15 — — [0.1,1] Doped fiber length Core radius Doped fiber core radius Doping radius Doped radius Numerical aperture Specifies numerical aperture of fiber 575 ER-YB CODOPED FIBER Doping Name and description Default value Default unit Units Value range Er ion density 5.14e+025 m-3 — [1,1e100] 6.2e+026 m-3 — [1,1e100] 10 ms — [1e-100, 1e100] 1.5 ms — [1e-100, 1e100] True — — True, False 5.2834e-024 m-3/s — [1e-100, 1e100] 3.44e-022 m-3/s — [1e-100, 1e100] 5.2834e-024 m-3/s — [1e-100, 1e100] 1000000000 1/s — [1,1e100] 1000000000 1/s — [1,1e100] Name and description Default value Default unit Units Value range OptiAmplifier format False — — True, False nm — — nm, m, Hz, THz Specifies Erbium doping in the fiber Yb ion density Specifies Ytterbium doping in the fiber Er metastable lifetime Specifies the Erbium metastable lifetime Yb metastable lifetime Specifies the Ytterbium metastable lifetime Calculate upconversion Component calculates C16 and C14 based on ion density C14 Cross relaxation coefficient between level 1 and 4 C16 Cross relaxation coefficient between level 1 and 6 Cup Homogeneous upconversion coefficient from level 2 A32 Nonradiative emission rate from level 3 to level 2 A43 Nonradiative emission rate from level 4 to level 3 Cross-sections Determines if format of cross-section file is an OptiAmplifier file File frequency unit Determines if the filter will down sample the signal bandwidth to the filter sample rate 576 ER-YB CODOPED FIBER Name and description Default value Default unit Units Value range Er cross-section file name Erbium.dat — — — Ytterbium.dat — — — Name and description Default value Default Unit Units Value range Loss data type Constant Signal loss 0.10 dB/m — [0,1e100] 0.15 dB/m — [0,1e100] Loss vs. wavelength Loss.dat — — — Include Rayleigh backscattering False — — True, False 150 dB/km — [0,1e100] Calculate — — Calculate, From file Capture.dat — — Constant, From File False — — True, False Calculate — — Calculate, From file 3000 μm — [1, 100000] Specifies Erbium cross-section file name Yb cross-section file name Specifies Ytterbium cross-section file name Enhanced Constant, FromFile Fiber loss at signal range Pump loss Fiber loss at pump range Determines the inclusion or not of the Rayleigh scattering effect Rayleigh constant Specifies the value of the Rayleigh constant Backscattering capture fraction Determines whether the capture fraction values will be calculated by the component or it will be loaded from a file Rayleigh capture file name Specifies the capture file name Double-clad fiber Specifies if the doped fiber is double-clad Double-clad data type Specify if the pump multimode absorption will be calculated by using the inner clad area or it will be loaded Cladding area 2 Specifies the inner clad section 577 ER-YB CODOPED FIBER Name and description Default value Default Unit Units Value range Pump absorption file name PumpAbsorptio n.dat — — — 300 K — [0,1000] False — — True, False 1550 nm — [500,1900] -20 ps/nm/km — [1e-100, 1e100] 0.005 ps/nm2/km — [1e-100, 1e100] Name and description Default value Default Unit Units Value range Include SPM False — — True, False Constant — — Constant, From file 50 um2 — [1e-100, 1e100] Effective Area.dat — — — Constant — — Constant, From file Specifies the absorption file name Temperature Absolute temperature Include Dispersion Defines whether to include dispersion effects or not Reference wavelength Used internally as “zero” (or reference) frequency in spectrum of signal envelope Dispersion Value of the GVD (Group Velocity Dispersion) parameter in wavelength domain. Dispersion slope Value of the dispersion slope parameter. Nonlinear effects Determines if the self-phase modulation will be taken into account. If True the optical signal will be propagated using the nonlinear Shrödinger equation. This parameter will also enable Crossphase modulation and Four-wave mixing effects. Effective area data type Defines is the effective area is constant or loaded from a file Effective area Defines value of the effective area Effective area file name Specifies the effective area filename n2 data type Defines if the nonlinear index is constant or loaded from a file 578 ER-YB CODOPED FIBER Name and description Default value Default Unit Units Value range n2 2.6e-020 m^2/W — [0,1e100] n2.dat — — — False — — True, False Constant — — Constant, From file 4.6e-011 m/W — Calculate, From file Brillouin.dat — — — 31.7 MHz — [1e-100, 1e100] 11 GHz — [1e-100, 1e100] False — — True, False Raman gain — — Raman gain, Raman gain efficiency 1e-013 — — [0, 1e100] 1000 nm — [0, 1e100] Raman Gain.dat — — — Nonlinear index value n2 file name Specifies the nonlinear index area filename Include Brillouin scattering Determines if the Brillouin scattering effect will be taken into account Brillouin gain data type Defines if the Brillouin gain is constant or loaded from a file Brillouin gain constant Brillouin gain value Brillouin gain file name Specifies the Brillouin gain file name Brillouin linewidth Specifies the Brillouin linewidth Frequency shift Specifies the Brillouin frequency shift Include Raman scattering Determines if the Raman scattering effect will be taken into account Raman gain data type Defines Raman gain type. If Raman gain efficiency is selected then the value in the raman gain file should be Raman gain / Effective area. Otherwise the file contain the normalized Raman gain that will be multiplied by the Raman gain peak Raman gain peak Raman gain peak that will multiply the normalized Raman gain Raman gain reference pump Value used in the Raman gain calculation Raman gain file name Specifies the normalized Raman gain file name or Raman efficiency file name 579 ER-YB CODOPED FIBER Name and description Default value Default Unit Units Value range Polarization factor 2 — — [1,2] Name and description Default value Default unit Units Value range Relative error 0.0001 — — [1e-100,1] 150 — — [1,1e8] 100 — — [1,1e8] 50 — — False — — True, False True — — True, False 100 GHz Hz, GHz, THz [1e9,1e12] 0.001 — — [1e-100, 1e100] Actual value depends on relative polarization of the fields. The value is 1 if the fields have aligned polarizations, and two if they have polarization scrambled Numerical Specifies maximum acceptable difference between two consecutive iterations to complete the iteration process Maximum number of iterations Specifies the maximum number of times for iteration process Longitudinal steps Specifies the number of longitudinal steps in the fiber Radial steps Specifies the number of radial steps for integration Numerical solver Defines whether the numerical solver is used instead of analytical solutions for the rate equations. Discretize sampled signal Defines whether to use a user defined discretization for sampled signals or not Frequency resolution Frequency spacing that will discretize the sampled signal Step tolerance Used in the Brillouin calculation and defines tolerance in the definition of length step 580 ER-YB CODOPED FIBER Graphs Name and description Default value Default unit Units Value range Calculate graphs False — — True, False Number of distance steps 20 — — [1,1e8] Number of wavelength steps 20 — — [1,1e8] Linear scale True — — True, False Minimum value -50 dBm — [1e-100, 1e100] Pump reference wavelength 1400 nm — [100, 1900] Name and description Default value Default unit Units Value range Enabled True — — True, False Longitudinal monitor True — — True, False Number of monitors 10 — — [1,1000] Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 THz Hz, GHz, THz, nm [1,1000] -100 dB — ]-INF, 0[ 3 dB — [0, +INF[ Simulation Defines whether the component is enabled or not Noise Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins space Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 581 ER-YB CODOPED FIBER Name and description Default value Default unit Units Value range Convert noise bins Convert noise bins — — True, False Name and description Default value Default unit Units Value range Generate random seed True — — True, False 0 — — [0, 4999] Determines if generated noise bins are incorporated into signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 582 ER-YB CODOPED FIBER Technical background Er-Yb Codoped Fiber Propagation and Rate Equations In order to give flexibility to change the waveguiding parameters of the Er3+ - Yb3+ codoped fiber for large signal and high pump power applications the extended model for Er3+ - Yb3+ codoped fiber presented in [1] is used. Figure 1 Energy levels for Er3+ - Yb3+ system Population densities of the4 11 ⁄ 2 and 4 9⁄2 levels of Er together with the upconversion from the pump level 4 3+ have been included . The model takes into 11 ⁄ 2 account propagation of the forward and backward amplified spontaneous powers for both the pump and the signal wavelength range. Depending on the pump wavelength, pump energy can be absorbed by both the Er ions in the 4 and by the Yb 3+ ions in the 2 F ground levels. Ytterbium ions 7⁄2 15 2 ⁄2 excited to the F5 ⁄ 2 level transfer their energy to neighboring Erbium ions in the 4 15 ⁄ 2 ground level, exciting them to the 4 relax to the metastable 4 13 ⁄ 2 11 ⁄ 2 pump level from where they rapidly level. The backtransfer from the Er pump level to the Yb ground level is neglected. 583 ER-YB CODOPED FIBER Let us denote the 4 ,4 ,4 3+ 4 9 ⁄ 2 levels of Er as levels 1, 2, 3+ Yb as levels 5 and 6, and their and the 13 ⁄ 22 11 ⁄ 2 2 15 ⁄ 2 3, and 4, and the F7 ⁄ 2 and the F5 ⁄ 2 levels of population densities as N1, N2, N3, N4, N5, and N6, respectively. The uniform upconversion mechanisms from the erbium metastable and pump levels are modeled by quadratic terms in N2 and N3, with a concentration dependent upconversion coefficient. The pair induced energy transfer process from Yb 3+ to Er 3+ is described by a cross relaxation coefficient [2]. The rate equations for the above atomic populations are: ∂N N 2 2 ---------1 = – W 12 N 1 – W 13 N 1 + ------2- + W 21 N 2 + C up N 2 – C 14 N1 N 4 + Cup N3 – C cr N1 N 6 ∂t τ Er ∂N2 N 2 --------- = W 12 N 1 – W 21 N2 – ------2- + A32 N 3 – 2C up N 2 + 2C 14 N1 N 4 ∂t τ Er (1) (2) ∂N 3 2 --------- = W 13 N1 – A 32 N 3 + A 43 N 4 – 2C up N 3 + C er N1 N 6 ∂t (3) ∂N4 2 2 --------- = 2C up N 2 – C14 N 1 N 4 – A 43 N 4 + C up N 3 ∂t (4) ∂N6 N --------- = W 56 N 5 – -------6- – W 65 N6 – C er N 1 N 6 ∂t τ Yb (5) W ij terms represent the stimulated transition rates between the i and j levels, τ Er , τ Yb are the spontaneous emission lifetimes for 4 and 13 ⁄ 2 2 F5 ⁄ 2 levels, A32 , A 43 are the nonradiative relaxation rates, and C up, C 14, C 16 are In these equations, the the upconversion and cross-relaxation coefficients. The signal absorption, signal emission, pump absorption, and pump emission rates,W 12, W 21, W 13, W 56, W 65are given by: σ 12 ( v s ) _ ∞ σ 12 ( v ) 2 + 2 - [ P ASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv W 12 ( r, z ) = ----------------- P s ( z ) E ( r, v s ) + ∫ --------------hv s hv 0 584 (6) ER-YB CODOPED FIBER σ 21 ( v s ) _ ∞ σ 21 ( v ) + 2 2 W 21 ( r, z ) = ----------------- P s ( z ) E ( r, v s ) + ∫ --------------- [ PASE ( z, v ) + PASE ( z, v ) ] ⋅ E ( r, v ) dv hv s hv 0 (7) σ 13 ( v p ) _ ∞ σ 13 ( v ) + 2 2 W 13 ( r, z ) = -----------------P p ( z ) E ( r, v p ) + ∫ --------------- [ PASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (8) σ 56 ( v p ) _ ∞ σ 56 ( v ) + 2 2 W 56 ( r, z ) = -----------------P p ( z ) E ( r, vp ) + ∫ --------------- [ P ASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (9) σ 65 ( v p ) _ ∞ σ 65 ( v ) 2 + 2 W 65 ( r, z ) = -----------------P p ( z ) E ( r, vp ) + ∫ --------------- [ P ASE ( z, v ) + PASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (10) σ 21 ( v ), σ 65 ( v ), σ 12 ( v ), σ 13 ( v ), and σ 56 ( v ) are the frequency dependent 3+ Er and Yb emission and absorption cross sections, respectively, h is the _ + Planck’s constant, P ASE ( z, v ) , P ASE ( z, v ) are the forward and backward propagating optical powers at frequency v in a frequency interval Δv , and at a longitudinal fiber coordinate z . They represent the forward and backward ASE powers due to the 4 -4 transition at 1400nm < λ < 1650nm , and also 13 ⁄ 2 2 15 ⁄ 2 2 the ASE powers due to the F5 ⁄ 2 - F7 ⁄ 2 transition at 850nm < λ < 1100nm . P s ( z ) is the signal power, P p ( z ) the pump power, v s, v p are the signal and pump frequencies, and E ( r, v ) is the field distribution of the LP 01 mode normalized where 3+ according to ∞ 2 2π ∫ E ( r, v ) r dr = 1 (11) 0 The total Er 3+ and Yb 3+ t t ion density distributions N Er , N Yb are assumed to be constant within the whole or a part of the fiber core, and along the fiber length (top hat shaped with the diameter of 2b). They satisfy the conservation equations t (12) N Er = N 1 ( r, z ) + N 2 ( r, z ) + N 3 ( r, z ) + N 4 ( r, z ) 585 ER-YB CODOPED FIBER t (13) N Yb = N 5 ( r, z ) + N 6 ( r, z ) Propagation of the pump power along the active fiber is described by the following differential equation: ∂P p ( z, vp ) b 2 ------------------------- = 2π ∫ [ σ 56 ( v p )N 5 ( r, z ) + σ 13 ( v p )N 1 ( r, z ) – σ 65 ( v p )N6 ( r, z ) ] E ( r, v p ) rdr + α ( v p ) P p ( z, vp ) ∂z 0 where b is the radius of Er 3+ - Yb 3+ (14) codoped part of the fiber core. The signal power and the ASE powers in both the pump and the signal wavelength range are amplified according to: ∂P s ( z, v s ) ----------------------- = [ g e ( z, v s ) – g a ( z, v s ) – α ( v s ) ]P s ( z, v s ) ∂z (15) ± ∂P ASE ( z, v ) ± ---------------------------- = ± 2hvΔvg e ( z, v s ) ± [ g e ( z, v ) – g a ( z, v ) – α ( v ) ] ( z, v s )P ASE ( z, v ) ∂z (16) α ( v ) is the frequency dependent background loss of the active fiber and the emission and absorption factors g e ( z, v ) , ( z, v ) are determined from the where corresponding emission and absorption cross sections as overlap integrals between the LP 01 intensity distribution and the population densities of the 2 F7 ⁄ 2, 4 15 ⁄ 2 2 F5 ⁄ 2, 4 levels defined in: ⎧ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…850nm < λ < 1100nm 65 ⎪ ∫0 6 g e ( z, v ) = ⎨ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…1400nm < λ < 1650nm 21 ⎪ ∫0 2 ⎩ ⎧ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…850nm < λ < 1100nm 56 ⎪ ∫0 5 g a ( z, v ) = ⎨ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…1400nm < λ < 1650nm 12 ⎪ ∫0 1 ⎩ 586 13 ⁄ 2 and (17) (18) ER-YB CODOPED FIBER These equations form a system of coupled differential equations that are solved by numerical integration along the active fiber, using the Runge-Kutta method. Population densities N 1 ( r, z ) , N 2 ( r, z ) , N 3 ( r, z ) , N 4 ( r, z ) , N 5 ( r, z ) , and N 6 ( r, z ) are derived from the steady-state solutions to the rate equations [1] - [5] together with conservation laws, equations [12] and [13] are substituted. Due to quadratic terms appearing in the rate equations, it is not possible to eliminate N 1 ( r, z ) , N 2 ( r, z ) , N 5 ( r, z ) , and N 6 ( r, z ) analytically, and so the numerical approach must be used. It was assumed that C 14 = C up and that the upconversion coefficient C up and the cross-relaxation coefficient C cr are linearly 1 1 increasing functions of N Er and N Yb respectively. densities C up = 3.5 × 10 – 24 + 2.41 × 10 – 22 + 4.0 × 10 C cr = 1.0 × 10 – 49 – 49 1 25 (19) 25 (20) ( N Er – 4.4 × 10 ) 1 ( N Yb – 1.0 × 10 ) References: [1] M. Karasek, "Optimum Design of Er3+ - Yb3+ Codoped Fibers for Large-Signal High-PumpPower Applications", IEEE Journal of Quantum Electronics, vol. 33, pp 1699-1705, 1997. [2] M. Federighi, F. Di Pasquale, "The Effect of Pair-induced Energy Transfer on the Performance of Silica Waveguide Amplifiers with High Er3+-Yb3+ Concentrations", IEEE Photon. Technol. Lett., vol 7, pp. 303-305, 1995. 587 ER-YB CODOPED FIBER Notes: 588 ER-YB CODOPED FIBER DYNAMIC Er-Yb Codoped Fiber Dynamic This component simulates a bidirectional Erbium-Ytterbium codoped fiber considering the simulation of dynamic effects. The component solves the rate and propagation equations numerically. Ports Name and description Port type Signal type Input1 Input Optical Output1 Output Optical Input2 Input Optical Output2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 1 m — [0,1000000] 2 μm — [1,1e100] 2 μm — [1,1e100] 0.15 — — [0.1,1] Doped fiber length Core radius Doped fiber core radius Doping radius Doped radius Numerical aperture Specifies numerical aperture of fiber 589 ER-YB CODOPED FIBER DYNAMIC Doping Name and description Default value Default unit Units Value range Er ion density 5.14e+025 m-3 — [1,1e100] 6.2e+026 m-3 — [1,1e100] 10 ms — [1e-100, 1e100] 1.5 ms — [1e-100, 1e100] True — — True, False 5.2834e-024 — m-3/s [1e-100, 1e100] 3.44e-022 — m-3/s [1e-100, 1e100] 5.2834e-024 — m-3/s [1e-100, 1e100] 1000000000 — 1/s [1,1e100] 1000000000 — 1/s [1,1e100] Name and description Default value Default unit Units Value range OptiAmplifier format False — — True, False nm — — nm, m, Hz, THz Specifies Erbium doping in the fiber Yb ion density Specifies Ytterbium doping in the fiber Er metastable lifetime Specifies the Erbium metastable lifetime Yb metastable lifetime Specifies the Ytterbium metastable lifetime Calculate upconversion Component calculates C16 and C14 based on ion density C14 Cross relaxation coefficient between level 1 and 4 C16 Cross relaxation coefficient between level 1 and 6 Cup Homogeneous upconversion coefficient from level 2 A32 Nonradiative emission rate from level 3 to level 2 A43 Nonradiative emission rate from level 4 to level 3 Cross-sections Determines if format of cross-section file is an OptiAmplifier file File frequency unit Determines if the filter will down sample the signal bandwidth to the filter sample rate 590 ER-YB CODOPED FIBER DYNAMIC Name and description Default value Default unit Units Value range Er cross-section file name Erbium.dat — — — Ytterbium.dat — — — Name and description Default value Default Unit Units Value range Loss data type Constant Signal loss 0.10 dB/m — [0,1e100] 0.15 dB/m — [0,1e100] Loss vs. wavelength Loss.dat — — — Double-clad fiber False — — True, False Calculate — — Calculate, Load from file 3000 μm — [1, 100000] PumpAbsorptio n.dat — — — Name and description Default value Default unit Units Value range Relative error 0.0001 — — [1e-100,1] Specifies Erbium cross-section file name Yb cross-section file name Specifies Ytterbium cross-section file name Enhanced Constant, FromFile Fiber loss at signal range Pump loss Fiber loss at pump range Specifies if the doped fiber is double-clad Double-clad data type Specify if the pump multimode absorption will be calculated by using the inner clad area or it will be loaded Cladding area 2 Specifies the inner clad section Pump absorption file name Specifies the absorption file name Numerical Specifies maximum acceptable difference between two consecutive iterations to complete the iteration process 591 ER-YB CODOPED FIBER DYNAMIC Name and description Default value Default unit Units Value range Maximum number of iterations 150 — — [1,1e8] 100 — — [1,1e8] 50 — — 0.5 / ( Bit rate ) s — [1,1e10] Name and description Default value Default unit Units Value range Calculate graphs False — — True, False Number of distance steps 20 — — [1,1e8] Number of wavelength steps 20 — — [1,1e8] Linear scale True — — True, False Minimum value -50 — dBm ]1e-100, 1e100[ Pump reference wavelength 1400 nm [100, 1900] Specifies the maximum number of times for iteration process Longitudinal steps Specifies the number of longitudinal steps in the fiber Radial steps Specifies the number of radial steps for integration Reference time Specifies the instant of time used to take the powers in the fiber to solve the steady-state regime Graphs Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Longitudinal monitor True — — True, False Number of monitors 10 — — [1,1000] Defines whether the component is enabled or not 592 ER-YB CODOPED FIBER DYNAMIC Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 13 THz Hz, THz, nm ]0,+INF[ 125 THz Hz, GHz, THz, nm [1,1000] -100 dB — ]-INF, 0[ 3 dB — [0, +INF[ Convert noise bins — — True, False Name and description Default value Default unit Units Value range Generate random seed True — — True, False 0 — — [0, 4999] Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins space Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if generated noise bins are incorporated into signal Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 593 ER-YB CODOPED FIBER DYNAMIC Technical background Er-Yb Codoped Fiber Propagation and Rate Equations In order to give flexibility to change the waveguiding parameters of the Er3+ - Yb3+ codoped fiber for large signal and high pump power applications the extended model for Er3+ - Yb3+ codoped fiber presented in [1] is used. Figure 1 Energy levels for Er3+ - Yb3+ system Population densities of the4 11 ⁄ 2 and 4 9⁄2 levels of Er together with the upconversion from the pump level 4 3+ have been included . The model takes into 11 ⁄ 2 account propagation of the forward and backward amplified spontaneous powers for both the pump and the signal wavelength range. Depending on the pump wavelength, pump energy can be absorbed by both the Er ions in the 4 and by the Yb 3+ ions in the 2 F ground levels. Ytterbium ions 7⁄2 15 2 ⁄2 excited to the F5 ⁄ 2 level transfer their energy to neighboring Erbium ions in the 4 15 ⁄ 2 ground level, exciting them to the 4 relax to the metastable 4 13 ⁄ 2 Yb ground level is neglected. 594 11 ⁄ 2 pump level from where they rapidly level. The backtransfer from the Er pump level to the ER-YB CODOPED FIBER DYNAMIC Let us denote the 4 ,4 ,4 3+ 4 9 ⁄ 2 levels of Er as levels 1, 2, 3+ Yb as levels 5 and 6, and their and the 13 ⁄ 22 11 ⁄ 2 2 15 ⁄ 2 3, and 4, and the F7 ⁄ 2 and the F5 ⁄ 2 levels of population densities as N1, N2, N3, N4, N5, and N6, respectively. The uniform upconversion mechanisms from the erbium metastable and pump levels are modeled by quadratic terms in N2 and N3, with a concentration dependent upconversion coefficient. The pair induced energy transfer process from Yb 3+ to Er 3+ is described by a cross relaxation coefficient [2]. The rate equations for the above atomic populations are: ∂N N 2 2 ---------1 = – W 12 N 1 – W 13 N 1 + ------2- + W 21 N 2 + C up N 2 – C 14 N1 N 4 + Cup N3 – C cr N1 N 6 ∂t τ Er ∂N2 N 2 --------- = W 12 N 1 – W 21 N2 – ------2- + A32 N 3 – 2C up N 2 + 2C 14 N1 N 4 ∂t τ Er (1) (2) ∂N 3 2 --------- = W 13 N1 – A 32 N 3 + A 43 N 4 – 2C up N 3 + C er N1 N 6 ∂t (3) ∂N4 2 2 --------- = 2C up N 2 – C14 N 1 N 4 – A 43 N 4 + C up N 3 ∂t (4) ∂N6 N --------- = W 56 N 5 – -------6- – W 65 N6 – C er N 1 N 6 ∂t τ Yb (5) W ij terms represent the stimulated transition rates between the i and j levels, τ Er , τ Yb are the spontaneous emission lifetimes for 4 and 13 ⁄ 2 2 F5 ⁄ 2 levels, A32 , A 43 are the nonradiative relaxation rates, and C up, C 14, C 16 are In these equations, the the upconversion and cross-relaxation coefficients. The signal absorption, signal emission, pump absorption, and pump emission rates,W 12, W 21, W 13, W 56, W 65are given by: σ 12 ( v s ) _ ∞ σ 12 ( v ) 2 + 2 - [ P ASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv W 12 ( r, z ) = ----------------- P s ( z ) E ( r, v s ) + ∫ --------------hv s hv 0 595 (6) ER-YB CODOPED FIBER DYNAMIC σ 21 ( v s ) _ ∞ σ 21 ( v ) + 2 2 W 21 ( r, z ) = ----------------- P s ( z ) E ( r, v s ) + ∫ --------------- [ PASE ( z, v ) + PASE ( z, v ) ] ⋅ E ( r, v ) dv hv s hv 0 (7) σ 13 ( v p ) _ ∞ σ 13 ( v ) + 2 2 W 13 ( r, z ) = -----------------P p ( z ) E ( r, v p ) + ∫ --------------- [ PASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (8) σ 56 ( v p ) _ ∞ σ 56 ( v ) + 2 2 W 56 ( r, z ) = -----------------P p ( z ) E ( r, vp ) + ∫ --------------- [ P ASE ( z, v ) + P ASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (9) σ 65 ( v p ) _ ∞ σ 65 ( v ) 2 + 2 W 65 ( r, z ) = -----------------P p ( z ) E ( r, vp ) + ∫ --------------- [ P ASE ( z, v ) + PASE ( z, v ) ] ⋅ E ( r, v ) dv hv p hv 0 (10) σ 21 ( v ), σ 65 ( v ), σ 12 ( v ), σ 13 ( v ), and σ 56 ( v ) are the frequency dependent 3+ Er and Yb emission and absorption cross sections, respectively, h is the _ + Planck’s constant, P ASE ( z, v ) , P ASE ( z, v ) are the forward and backward propagating optical powers at frequency v in a frequency interval Δv , and at a longitudinal fiber coordinate z . They represent the forward and backward ASE powers due to the 4 -4 transition at 1400nm < λ < 1650nm , and also 13 ⁄ 2 2 15 ⁄ 2 2 the ASE powers due to the F5 ⁄ 2 - F7 ⁄ 2 transition at 850nm < λ < 1100nm . P s ( z ) is the signal power, P p ( z ) the pump power, v s, v p are the signal and pump frequencies, and E ( r, v ) is the field distribution of the LP 01 mode normalized where 3+ according to ∞ 2 2π ∫ E ( r, v ) r dr = 1 (11) 0 The total Er 3+ and Yb 3+ t t ion density distributions N Er , N Yb are assumed to be constant within the whole or a part of the fiber core, and along the fiber length (top hat shaped with the diameter of 2b). They satisfy the conservation equations t N Er = N 1 ( r, z ) + N 2 ( r, z ) + N 3 ( r, z ) + N 4 ( r, z ) 596 (12) ER-YB CODOPED FIBER DYNAMIC t (13) N Yb = N 5 ( r, z ) + N 6 ( r, z ) Propagation of the pump power along the active fiber is described by the following differential equation: ∂P p ( z, vp ) b 2 ------------------------- = 2π ∫ [ σ 56 ( v p )N 5 ( r, z ) + σ 13 ( v p )N 1 ( r, z ) – σ 65 ( v p )N6 ( r, z ) ] E ( r, v p ) rdr + α ( v p ) P p ( z, vp ) ∂z 0 where b is the radius of Er 3+ - Yb 3+ (14) codoped part of the fiber core. The signal power and the ASE powers in both the pump and the signal wavelength range are amplified according to: ∂P s ( z, v s ) ----------------------- = [ g e ( z, v s ) – g a ( z, v s ) – α ( v s ) ]P s ( z, v s ) ∂z (15) ± ∂P ASE ( z, v ) ± ---------------------------- = ± 2hvΔvg e ( z, v s ) ± [ g e ( z, v ) – g a ( z, v ) – α ( v ) ] ( z, v s )P ASE ( z, v ) ∂z (16) α ( v ) is the frequency dependent background loss of the active fiber and the emission and absorption factors g e ( z, v ) , ( z, v ) are determined from the where corresponding emission and absorption cross sections as overlap integrals between the LP 01 intensity distribution and the population densities of the 2 F7 ⁄ 2, 4 15 ⁄ 2 2 F5 ⁄ 2, 4 levels defined in: 13 ⁄ 2 ⎧ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…850nm < λ < 1100nm 65 ⎪ ∫0 6 g e ( z, v ) = ⎨ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…1400nm < λ < 1650nm 21 ⎪ ∫0 2 ⎩ and (17) ⎧ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…850nm < λ < 1100nm 56 ⎪ ∫0 5 g a ( z, v ) = ⎨ ⎪ 2πσ ( v ) b N ( r, z ) E ( r, v ) 2 r dr…1400nm < λ < 1650nm 12 ⎪ ∫0 1 ⎩ 597 (18) ER-YB CODOPED FIBER DYNAMIC These equations form a system of coupled differential equations that are solved by numerical integration along the active fiber, using the Runge-Kutta method. Population densities N 1 ( r, z ) , N 2 ( r, z ) , N 3 ( r, z ) , N 4 ( r, z ) , N 5 ( r, z ) , and N 6 ( r, z ) are derived from the steady-state solutions to the rate equations [1] - [5] together with conservation laws, equations [12] and [13] are substituted. Due to quadratic terms appearing in the rate equations, it is not possible to eliminate N 1 ( r, z ) , N 2 ( r, z ) , N 5 ( r, z ) , and N 6 ( r, z ) analytically, and so the numerical approach must be used. It was assumed that C 14 = C up and that the upconversion coefficient C up and the cross-relaxation coefficient C cr are linearly 1 1 increasing functions of N Er and N Yb respectively. densities C up = 3.5 × 10 – 24 + 2.41 × 10 – 22 + 4.0 × 10 C cr = 1.0 × 10 – 49 – 49 1 25 (19) 25 (20) ( N Er – 4.4 × 10 ) 1 ( N Yb – 1.0 × 10 ) References: [1] M. Karasek, "Optimum Design of Er3+ - Yb3+ Codoped Fibers for Large-Signal High-PumpPower Applications", IEEE Journal of Quantum Electronics, vol. 33, pp 1699-1705, 1997. [2] M. Federighi, F. Di Pasquale, "The Effect of Pair-induced Energy Transfer on the Performance of Silica Waveguide Amplifiers with High Er3+-Yb3+ Concentrations", IEEE Photon. Technol. Lett., vol 7, pp. 303-305, 1995. 598 ER-YB CODOPED WAVEGUIDE AMPLIFIER Er-Yb Codoped Waveguide Amplifier This component simulates an Er-Yb codoped waveguide amplifier based on basic parameters. Ports Name and description Port type Signal type Input1 Input Optical Output1 Output Optical Input2 Input Optical Output2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Waveguide length 0.03 — m ]0,+INF[ Signal background loss 0 — db/m [0,+INF[ db/m [0,+INF[ Represents the intrinsic material losses, given by the losses at 1300nm. Pump background loss 0 Represents the intrinsic material losses, given by the losses at 1300nm. Refractive index data file Index.rid — — — Erdensity.dat — — — Same as OptiBPM’s refractive index file. Contains a uniform refractive index distribution and follows the format defined in OptiBPM. Also contains the number of points used to discretize the domain. Er ion density distribution file Same as Refractive index data file, contains the Erbium ion density distribution. File must have the same discretization as the Refractive index data file, and must be filled with ones and zeros. 599 ER-YB CODOPED WAVEGUIDE AMPLIFIER Name and description Default value Default unit Units Value range Yb ion density distribution file Ybdensity.dat — — — True — — True, False nm [1490, 3000] Same as Er ion density distribution file, contains the Ytterbium ion density distribution. File must have the same discretization as the Refractive index data file, and must be filled with ones and zeros. Calculate mode in all wavelengths Identifies if a mode must be calculated for all the signal wavelengths. If selected, the mode solver is activated, using the refractive index distribution defined in a file for all the signal wavelengths. Wavelength to calculate the mode 1550 If Calculate mode in all wavelength is not selected, a signal mode, calculated at the defined wavelength, is shared for all signals. This selections makes the calculation faster after the part of the execution time is spent calculating the modes. Recalculate modes every running False — — False, True TE — — TE, TM 2 — — [1, 10] TE — — TE, TM 0.5 0.5 — — any string with numbers Name and description Default value Default unit Units Value range Er ion density 1e+025 m-3 [0, +INF[ Identifies if all the modes, in the pump and signal wavelengths, must be recalculated. It is suggested that this option not be selected, due to the excessive time spent recalculating the modes. Polarization for signal mode calculation Polarization used to calculate the signal modes. Number of modes at pump wavelength Number of modes that are calculated at the pump wavelength. Read-only value. To change it, edit the “Power ratio for each pump mode” option. Polarization for pump mode calculation Polarization used to calculate the pump’s modes. Power ratio for each pump mode Power ratio for each pump mode. Number of elements in the list must be equal to the number of modes at the pump wavelength, and the sum of the ratios must be 1. Doping Specifies Erbium doping in the fiber 600 ER-YB CODOPED WAVEGUIDE AMPLIFIER Name and description Default value Er metastable lifetime Default unit Units Value range 11 ms ]0, +INF[ 0 dB/m [0, +INF[ 0 dB/m [0, +INF[ 1e+025 m-3 [0, +INF[ 11 ms ]0, +INF[ 0 dB/m [0, +INF[ 0 dB/m [0, +INF[ Specifies the Erbium metastable lifetime Er signal excess loss Represents the losses, due to the introduction of Erbium in the material by diffusion or by another implantation method, at the signal wavelength. Backscattering is a typical effect observed in this case. Note: This isn’t a commonly observed absorption loss in the 1550nm wavelength range. Er pump excess loss Represents the losses, due to the introduction of Erbium in the material by diffusion or by another implantation method, at the pump wavelength. Backscattering is a typical effect observed in this case. Note: This isn’t a commonly observed absorption loss at 980nm. Yb ion density Specifies Ytterbium doping in the fiber Yb metastable lifetime Specifies the Ytterbium metastable lifetime Yb signal excess loss Represents the losses, due to the introduction of Ytterbium in the material by diffusion or by another implantation method, at the signal wavelength. Backscattering is a typical effect observed in this case. Yb pump excess loss Represents the losses, due to the introduction of Ytterbium in the material by diffusion or by another implantation method, at the pump wavelength. Backscattering is a typical effect observed in this case. Cross-sections Name and description Default value Default unit Units Value range EDFA design format False — — True, False nm — — nm, m, Hz, THz Determines if format of cross-section file uses EDFA file format File frequency unit Determines if the filter will down sample the signal bandwidth to the filter sample rate 601 ER-YB CODOPED WAVEGUIDE AMPLIFIER Name and description Default value ESA cross section value at 1480 5.53-026 Er cross-section file name Erbium.dat Default unit Units Value range m2 ]0, +INF[ — — — Ytterbium.dat — — — Name and description Default value Default Unit Units Value range Number of ASE models 2 — — [1, 1e+008] 1000000000 — 1/s ]0, +INF[ 1000000000 — 1/s ]0, +INF[ 0 — — [0, 1] s ]0, +INF[ Specifies Erbium cross-section file name. File contains erbium absorption and emission cross sections. Yb cross-section file name Specifies Ytterbium cross-section file name. File contains the ytterbium absorption and emission cross sections. Enhanced Quantity of excited modes by the ASE. Normally this number is the total number of modes (TE and TM) present in the waveguide at the signal wavelength. A32 Nonradiative emission rate from level 3 to level 2 A43 Nonradiative emission rate from level 4 to level 3 Fraction of ion in pair Fraction of ion in pair due to the pair-induced quenching PIQ phenomenon. Fast nonradiative upconversion lifetime 5e-006 Calculate upconversion effects True — — True, False 1e-022 — m3/s ]0, +INF[ 1e-022 — m3/s ]0, +INF[ 7e-023 — m3/s ]0, +INF[ Define whether the upconversion effects are calculated or just approximated. Cup Homogeneous upconversion coefficient from level 2 C3 Homogeneous upconversion coefficient from level 3 C14 Cross relaxation coefficient between level 1 and 4 602 ER-YB CODOPED WAVEGUIDE AMPLIFIER Name and description Default value Default Unit Units Value range C16 7e-023 — m3/s ]0, +INF[ Name and description Default value Default unit Units Value range Relative error 5e-007 — — ]0, 1] 130 — — [1,1e+008[ Name and description Default value Default unit Units Value range Calculate graphs True — — True, False Longitudinal power graphs True — — True, False Normalized population density graphs True — — True, False Name and description Default value Default unit Units Value range Enabled True — — True, False Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 13 THz Hz, THz, nm ]0,+INF[ Cross relaxation coefficient between level 1 and 6 Numerical Specifies maximum acceptable error in solving the propagation equations Longitudinal steps Specifies the number of divisions necessary to discretize the waveguide length Graphs Simulation Defines whether the component is enabled or not Noise Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins 603 ER-YB CODOPED WAVEGUIDE AMPLIFIER Name and description Default value Default unit Units Value range Noise bins space 125 GHz Hz, GHz, THz, nm [1,1000[ -100 dB — ]-INF, 0[ 3 dB — [0, +INF[ Convert noise bins — — True, False Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaption of noise bins Convert noise bins Determines if generated noise bins are incorporated into signal Technical background The Er-Yr codoped waveguide amplifier solves the propagation of electromagnetic fields on Erbium doped, or on Erbium doped and Ytterbium co-doped waveguides. The pump wavelength must be in the region of 980 nm or 1480 nm, and can be coand counter-propagating. Multiple co- and counter-propagating input signals may be considered in different wavelengths (DWDM). In order to run this component, the following data must be provided: the Erbium and Ytterbium doping profiles, with their respective cross sections (parameters located in the cross-sections tab); the pump wavelength ( λ p ) with the co- and counterpropagant pump powers ( P p+, P p _ ); and the WDM signal wavelengths 1 WDM ( λ s …λ s ) with its respective powers. Notice that a signal is characterized by its wavelength, and may have different co and counter-propagant powers i i ( λ s → P s+ i and P s- ). The main characteristics of this component are: • co- and counter-propagant pump at 980nm region or 1480nm region; • multiple signals (co- and counter-propagant) at different wavelengths (DWDM); • multimode operation for the pump and signals; • co- and counter-propagant ASE noise due to Erbium concentration; • homogeneous upconversion (HUC) 1 from • pair-induced quenching - PIQ; • nine energy levels considered. 4 13 ⁄ 2 e4 11 ⁄ 2 levels; Model implementation This model is based on the solution of the propagation equations, using, directly, the solutions of the involved electromagnetic fields and the exact Erbium and Ytterbium transversal distributions. 604 ER-YB CODOPED WAVEGUIDE AMPLIFIER Propagation equations The propagation equations describe the power evolution of the propagating electromagnetic fields in the optical amplifier and are described as: dP p +_ ( z ) --------------------- = − + γ p ( z )P p+_ ( z ) − + αp P p+_ ( z ) dz i (1) i dP s+_ ( z, v s ) i i i i i i ----------------------------- = − + [γ 21 ( z, v s ) – γ 12 ( z, v s )] P s ( z, v s ) − + α p P s ( z, v s ), i = 1, …, WDM dz dP j ASE +_ ( z, v j ) = ± [ γ 21 ( z, v j ) – γ 12 ( z, v j ) ]P ± mhv j Δv j γ 21 ( z, v j ) ± α s P j ASE +_ ( z, v s ), j ASE + _ (2) ( z, v s ) + (3) j = 1, …, M This set of equations forms a system of 2+2WDM+2M coupled ones, and must be solved with the following boundary conditions: (4) P p+ ( 0 ) = P p0, P p _ ( L ) = P pL i i P s+ ( 0, v is ) = P s0 ( v is ) and P s _ ( L, v is ) = PsL ( v is ), i = 1, …WDM (5) PASE + ( 0, v s ) = P ASE _ ( L, vj ) = 0, j = 1, …, M (6) where L is the device length i P s+_ , P p +_ , e , and P j ASE +_ are the signals, pumps and ASE (Amplified Spontaneous Emission) longitudinal power distributions in the direction of propagation z , with the signs (+) and (-) meaning, respectively, the co- and counter propagant direction; α s and α p are the attenuation coefficients in the wavelengths for signal and pumping, respectively. The index i i i in P s+_ refers to the i -th signal, centered in the frequency v s , of a total number of WDM signals that can propagate simultaneously within the amplifier, as in systems with Dense Wavelength Division Multiplex - DWDM. The ASE± spectrum is Δv j , centered in the frequencies (see Equation 3) refers to the j -th spectral discretized in M intervals (slots) with spectral width v j , in such a way, that P j ASE +_ 605 ER-YB CODOPED WAVEGUIDE AMPLIFIER component of ASE±. Also in Equation 3, we have m as the total number of modes h is the Planck constant. In Equation 1 - Equation 3, the gain coefficients γ p , γ 12 , and γ 21 are given by: present in the waveguide, and γp ( z ) = ∫ ∫ Ψp ( x, y ) [ σa13 ( N1 ( x, y, z ) + 2N0p ( x, y, z ) + N1p ( x, y, z ) ) A (7)a – σ e31 N 3 ( x, y, z ) + σ a56 N 5 ( x, y, z ) – σ e65 N 6 ( x, y, z ) ]dxdy γp ( z ) = ∫ ∫ Ψp ( x, y ) [ σa13 ( N1 ( x, y, z ) + 2N0p ( x, y, z ) + N1p ( x, y, z ) ) + A (7)b – σ e31 ( N 2 ( x, y, z ) + N 3 ( x, y, z ) + 2N 0p ( x, y, z ) + N 1p ( x, y, z ) ) ]dxdy γ 12 ( z, v i ) = ∫ ∫ Ψs ( x, y )σ a12( N1 ( x, y, z ) + 2N0p ( x, y, z ) + N1p ( x, y, z ) ) dx dy (8) ∫ ∫ Ψs ( x, y )σe21 ( N2 ( x, y, z ) + 2N2p ( x, y, z ) + N1p ( x, y, z ) ) dx dy (9) A γ 21 ( z, v i ) = A N 1 , N 2 , and N 3 , are the populations of Erbium ions of the ground ( 4 15 ⁄ 2 ), meta-stable( 4 ) and pump levels ( 4 if pumped in 1480nm, or 4 if 13 ⁄ 2 13 ⁄ 2 11 ⁄ 2 pumped in 980nm). N 5 and N 6 are the populations of Ytterbium ions of levels 2 2 F7 ⁄ 2 and F5 ⁄ 2 . where The populations of three possible states of an excited pair exist: N 0p - no ion excited N 1p - one ion excited N 2p - two ions excited due to the phenomenon of pair-induced quenching - PIQ. σ a13 , σ e31 , σ a12 , and σ e21 are the absorption and emission cross sections of the Erbium doped material, at the signal (12 and 21) and pump (13 and 31) wavelengths. The parameters σ a56 and σ e65 are the absorption and emission cross sections of the Ytterbium doped/codoped material at the pump wavelength in the region of 980nm. When the amplifier is pumped at 980nm, the level 3 corresponds to the main level 4 11 ⁄ 2 of the Stark Split. However, when the amplifier is pumped in the 1480nm region, the pump level is confounded with the main level 606 4 13 ⁄ 2 . Thus, according to Equation 7a or ER-YB CODOPED WAVEGUIDE AMPLIFIER Equation 7b, the coefficient of gain γ p is taken when the amplifier is pumped at 980nm or 1480nm, respectively. In Equation 7 through to Equation 9, Ψ s ( x, y ) and Ψ p ( x, y ) are the normalized intensity profiles obtained from the modal analysis of the waveguide (see the section on "Multimode operation"), in such a way that the intensity distributions of the signal, pump and ASE± can be written as: I s ( x, y, z ) = Ψ s ( x, y )P s ( z ) (10) I p ( x, y, z ) = Ψ p ( x, y )P p ( z ) (11) j j (12) I ASE +_ ( x, y, z ) = Ψ s ( x, y )P ASE +_ ( z ) where it should be noted that the same normalized intensity profile has been used for ASE and signal, because the difference between the central wavelengths of the M intervals used to discretize the ASE and the signal wavelength is relatively small and may be considered j i Ψ ASE ≈ Ψ s . The correlation between the field distribution of the fundamental mode at 1530nm and 1650nm is higher than 95% for a typical optical fiber/waveguide. Rate equations N 1 → N 6 , and also the population of the three possible states of an excited pair ( N 0p , N 1p , and N 2p ) in Equation 7 through to Equation 9, are the The populations solutions of the rate equations for the energetic systems of Figure 1 or Figure 2, when it is considered the pumping in 980nm or 1480nm, respectively. 607 ER-YB CODOPED WAVEGUIDE AMPLIFIER Figure 1 Coupled Er+3/Yb+3 system, pumped in 980nm region Note: There are nine relevant energy levels considered (four levels due to the presence of the Erbium ions, two due to the Ytterbium dopant, and three due to the formation of Erbium paired-induced ions). R ij 's and W ij 's are the pump and signal stimulated rates,and the A ij 's are the nonradioactive rate from level i to j. A21 is the fluorescent rate. Cup and C3 are the homogeneous upconversion coefficients. C14 and C16 are the cross-relaxation coefficients. Figure 1 also shows the population densities of the three possible states of an excited pair ( N 0p (no ions excited), N 1p (one ion excited), and N 2p (two ions excited), due to the PIQ effect. In Figure 1, for the 980nm-pumping region, we have representations of the 4 13 ⁄ 2 , 4 11 ⁄ 2 , and 4 9⁄2 energy levels (due to the Erbium dopant), with F5 ⁄ 2 15 ⁄ 2 , 2 N i ( i = 1, 4 ) , respectively. The F7 ⁄ 2 and energy levels are also shown, with population densities N i ( i = 5, 6 ) , due to corresponding population densities of 2 4 the Ytterbium dopant. The populations of the three possible states of an excited ion 608 ER-YB CODOPED WAVEGUIDE AMPLIFIER ( N 0p , N 1p , and N 2p ) are also shown. τ 21p is the fast nonradiative upconversion lifetime, and can be calculated as: 3 τ 21p with d pair = ---------C up (13) d pair being the distance between two ions in a pair. Experimental measurements report typical value of the order of few microseconds. We know that R ij ‘s are pump rates (stimulated absorption and emission) between levels i → j , and W ij 's are the absorption and emission stimulated rates at the signals wavelength. The non-radiative rates between levels i → j are represented by A ij . A21 is the fluorescence rate. Cup and C3 are the homogeneous upconversion coefficients from levels 2 and 3. The homogeneous upconversion is modeled through the quadratic terms in N2 and N3 in the rate equations. These terms are dependent on the Erbium concentration, and can be calculated using reference [1]. C14 and C16 are the cross-relaxation coefficients between levels relaxation between levels 4 → 1 and 6 → 1 . The cross- 6 → 1 is the main energy transfer mechanism between the Ytterbium and Erbium ions, and the approached value of the coefficient can be obtained from [1]. Due to the short lifetime of level 3 ( 1 ⁄ A 32 ), the back energy transfer process (from Erbium to Ytterbium ions) is not being considered in this model. However, the fact that all Erbium ions are surrounded by Ytterbium ions is taken into account. Special attention should be paid to the Ytterbium concentration in relation to the Erbium concentration. Geometrically, it is observed that the Ytterbium concentration must be in the interval 4N Er < N Yb < 20N Er . If the Ytterbium 4N Er , the formation of clusters may occur and the +3 +3 energy transference form Ytterbium ions ( Yb ) to the Erbium ones ( Er ) may not concentration ( N Yb ) is less than be so efficient. On the other hand, if the Ytterbium concentration is too high, Ytterbium clusters may form, which means there won't be any energy transference to the Erbium ions, the pump energy will be wasted, and consequently, the efficiency of the amplifier device will be reduced. It is believed that the homogeneous upconversion that occurs from level 3 doesn't reach level 4 F7 ⁄ 2 and relaxes very quickly to level 4 ( 4 609 9⁄2 ). ER-YB CODOPED WAVEGUIDE AMPLIFIER The rate equations for the energy system of Figure 2 is given by: ∂N ---------1 = – W 12 N 1 – R 13 N 1 + R 31 N 3 + A 21 N 2 + W 21 N 2 + ∂t 2 2 + C up N 2 – C 14 N 1 N 4 + C 3 N 3 – C 16 N 1 N 6 ∂N 2 --------- = W 12 N 1 – A 21 N 2 – W 21 N 2 + A 22 N 3 + ∂t 2 – 2C up N 2 + 2C 14 N 1 N 4 ∂N 2 ---------3 = R 13 N 1 – R 31 N 3 – A32 N 3 + A43 N 4 – 2C 3 N 3 + C 16 N 1 N 6 ∂t N 1 + N 2 + N 3 + N 4 = ( 1 – 2p )N Er ∂N ---------5 = – R56 N 5 + A65 N 6 + R 65 N 6 + C 16 N 1 N 6 ∂t (14) N 5 + N 6 = N Yb ∂N 0p ------------ = – 2R 13 N 0p + A 21 N 1p –2W 12 N 0p + W 21 N 1p ∂t ∂N 1p ------------ = + 2R 13 N 0p – A 21 N 1p + 2 W 12 N 0p – W 21 N 1p + 2A21 N 2p + ∂t N 2p – R13 N 1p – W12 N 1p + 2W 21 N 2p + --------τ 21p N 0p + N 1p + N 2p = pN Er The presence of the crossed terms N i N j for the solutions of the population N i ( i = 1 → 6 ) , suggests the use of a special numeric treatment due to its non-linear nature. However, the system for the paired-induced population is a linear one and can be solved by a straightforward solution. 610 ER-YB CODOPED WAVEGUIDE AMPLIFIER The solution for the paired-induced population when the amplifier is pumped at 980nm is given by: N 0p = – ( N 1p – pN Er + 3A 21 N 1p τ 21p + N 1p R13 τ 21p – 2A21 pN Er τ 21p + N 1p τ 21p W 12 + 3N 1p τ 21p W 21 – 2pN Er τ 21p W 21 ) ⁄ ( 1 + 2A 21 τ 21p – 2R 13 τ 21p – 2τ 21p W 12 + 2τ 21p W 21 ) N 1p (15) ( 2N 0p ( R 13 + W 12 ) ) = ---------------------------------------------( A 21 + W 21 ) N 2p = pN Er – N 0p – N 1p Figure 2 shows the system of energy levels that are being taken into account for the 1480nm pumping wavelength, as well as the numbering of these levels. In this case the pump energy level belongs to the main level 2 ( 4 13 ⁄ 2 presence of the nonradioactive transitions inside the level ). However, due to the 4 13 ⁄ 2 , we have named the pump level as "level 3". Note that it should not be confused with the level 4 when the system is pumped at 980nm region. Figure 2 Coupled Er+3/Yb+3 system, pumped at 1480nm region 611 11 ⁄ 2 , ER-YB CODOPED WAVEGUIDE AMPLIFIER Note: There are nine relevant energy levels considered (four levels due to the presence of the Erbium ions, two due to the Ytterbium dopant, and three due to the formation of Erbium paired-induced ions). R ij 's and W ij 's are the pump and signal stimulated rates,and the A ij 's are the nonradioactive rate from level i to j. A21 is the fluorescent rate. Cup and C3 are the homogeneous upconversion coefficients. C14 and C16 are the cross-relaxation coefficients. Figure 2 also shows the population densities of the three possible states of an excited pair ( N 0p (no ions excited), N 1p (one ion excited), and N 2p (two ions excited), due to the PIQ effect. When the system is pumped in the 1480nm region, levels 5 and 6 (Ytterbium levels) are considered to be empty. It is known that the effects of ESA cannot be disregarded when the pumping wavelength is at 1480nm region, because the ESA cross section is approximately 10% of the peak value of the absorption cross section. The non-radioactive rate embodies the non-radioactive rates between levels 4 11 ⁄ 2 →4 13 ⁄ 2 , in such a way that level 4 11 ⁄ 2 4 9⁄2 →4 11 ⁄ 2 A 43 and is not considered. In this case, the system of rate equations is then described as: ∂N 1 2 --------- = – W 12 N 1 – R 13 N 1 + R31 N 3 + A 21 N 2 + W 21 N 2 + C up N 2 – C 14 N 1 N 4 ∂t ∂N 2 2 ESA --------- = W 12 N 1 – A 21 N 2 – W 21 N 2 + A 32 N 3 – 2C up N 2 + 2C 14 N 1 N 4 – R 24 N 2 ∂t ∂N 3 --------- = R 13 N 1 – R 31 N 3 – A 32 N 3 + A 43 N 4 ∂t N 1 + N 2 + N 3 + N 4 = ( 1 – 2p )N Er ∂N 0p ----------- = – 2R 13 N 0p + A 21 N 1p – 2W 12 N 0p + W 21 N 1p ∂t ∂N 1p ------------ = + 2R 13 N 0p – R 31 N 1p – A 21 N 1p + 2W 12 N 0p – W 21 N 1p + 2A 21 N 2p + ∂t N 2p – R13 N 1p + 2R 31 N 2p– W 12 N 1p + 2W 21 N 2p + --------τ 21p N 0p + N 1p + N 2p = pN Er 612 (16) ER-YB CODOPED WAVEGUIDE AMPLIFIER R ij and W ij are the simulated rates between levels i → j , at the pump ( R ) and signals ( W ) wavelengths. A ij are the non-radioactive rates between levels i → j , and A21 is the fluorescence rate. Cup and C14 are the homogeneous upconversion ESA R24 is the ESA rate for level 2 and level 4. The presence of the crossed terms N i N j in Equation 16 suggests the use of a numeric solution for the populations N 1 → N 6 . However, the system for the pairedand the cross-relaxation coefficients. induced population is a linear one and can be solved by a straightforward solution. The solution for the paired-induced population when the amplifier is pumped at 1480nm is given by: N 0p = – ( pN Er ( 1 + 2A 21 τ 21p + 2R 31 τ21p + 2τ 21p W 21 ) ) ⁄ ( – 1 – 2A21 + 2R 13 τ21p – 2R31 τ 21p + 2τ 21p W 21 _ 2 ( R 13 + W 12 ) ( 1 + 3A 21 τ 21p + R13 τ 21p + 3R 31 τ 21p + τ21p W 12 + 3τ21p W 21 ) ⁄ ( A21 + R 31 + W 21 ) ) N 1p (17) ( 2N0p ( R13 + W 12 ) ) = ---------------------------------------------( A21 + R 31 + W 21 ) N 2p = pN Er – N 0p – N 1p In the stationary state, the solutions of the rate Equation 14 and Equation 16 are obtained by nullifying the left side of these equations. As we have previously stated, the systems of Equation 14 and Equation 16 are non-linear due to the presence of the N 1 N 4 and N 1 N 6 , and must be solved numerically. The stimulated rates W ij and R ij are written as: crossed terms WDM W 12 ( x, y, z, vs ) = ∑ i=1 M j i i σ a12 ( v s ) i i i i ------------------- ( I s+ ( x, y, z, v s ) + I s _ ( x, y, z, v s ) ) + i hv s j σ a12 ( v ) j j j j - ( I ASE+ ( x, y, z, v ) + I ASE _ ( x, y, z, v ) ) + ∑ ------------------j hv j=1 613 (18)a ER-YB CODOPED WAVEGUIDE AMPLIFIER WDM ∑ W 21 ( x, y, z, v s, v p ) = i=1 i i σ e21 ( v s ) i i i i -------------------- ( I s+ ( x, y, z, v s ) + I s _ ( x, y, z, vs ) ) + i hv s σ ep21 ( v p ) + ---------------------- ( I p+ ( x, y, z, v p ) + I p _ ( x, y, z, v p ) ) + hv p M j (18)b j σ e21 ( v ) j j j j ( I ASE+ ( x, y, z, v ) + I ASE _ ( x, y, z, v ) ) + ∑ ------------------j hv j=1 σ a13 ( v p ) R 13 ( x, y, z, v p ) = -------------------- ( I p+ ( x, y, z, v p ) + I p_ ( x, y, z, v p ) ) hv p σ e31 ( v p ) R 31 ( x, y, z, v p ) = -------------------( I p+ ( x, y, z, vp ) + I p_ ( x, y, z, v p ) ) hv p (18)c (18)d σ a56 ( v p ) - ( I p+ ( x, y, z, v p ) + I p_ ( x, y, z, v p ) ) R 56 ( x, y, z, v p ) = -------------------hv p (18)e σ e65 ( v p ) R 65 ( x, y, z, v p ) = -------------------( I p+ ( x, y, z, vp ) + I p_ ( x, y, z, v p ) ) hv p (18)f ESA R 24 ( x, WDM ∑ y, z, v s, v p ) = i=1 i σ a24 ( v s ) i i i i -------------------- ( I s+ ( x, y, z, v s ) + I s _ ( x, y, z, v s ) ) + i hv s σ a24 ( v p ) + -------------------- ( I p+ ( x, y, z, v p ) + I p_ ( x, y, z, vp ) ) + hv p M j (18)g j σ a24 ( v ) j j j j + ∑ ------------------- ( I ASE+ ( x, y, z, v ) + I ASE _ ( x, y, z, v ) ) j hv j=1 ESA = σ ep21 = 0 when the pumping wavelength is in the 980nm region. When the pumping wavelength is in the 1480nm region, we have σ ep21 = σ ep31 and R 56 = R 65 = 0 . In Equation 18, it is presumed that the propagation of WDM i signals with frequencies v s and intensities I +_ ; pumping intensities I +_ ; and s p ASE(Amplified Spontaneous Emission) with its spectrum discretized in M slots of Δv where 614 R 24 ER-YB CODOPED WAVEGUIDE AMPLIFIER width with intensity I . The sign "+" refer to the co-propagant waves, and the ASE +_ sign "-" to the counter-propagant waves. The use of the homogeneous upconversion and the cross-relaxation coefficients and consideration of the PIQ phenomenon in Equation 14 and Equation 16 allows for the adequate modeling of Erbium doped and Ytterbium co-doped waveguides. In general, for Erbium concentrations in the order of 100ppm ("1024 ions/m3) these effects are not important. However, the present applications of optical amplifiers demand Erbium concentrations higher than 1000ppm, and, therefore, such effects cannot be ignored. Multimode operation The doped waveguide may present more than one mode at the pump or at the signal frequencies/wavelength. This is common in integrated optics, in which the discontinuity between the refraction index of the core and the cladding is raised on purpose to provoke a high confinement of the pump field and, thus, obtain higher gain [1]. We can presume that the device is externally excited by a beam with gaussian field distribution Φ ( x, y, ω ) , with different spatial widths at the pump and signal wavelengths. This supposition is experimentally sustained when a beam that it is being coupled through a set of lenses excites an integrated optical device. Consider λ s and λ p (signal and pump wavelength, respectively), N s i and N p modes with fields distributions φ ( x, y, λ s ⁄ p ) can propagate. The input that at the wavelengths beam can then be described through a modal expansion of the modes present in the waveguide, that is: Nq Φ ( x, y, λ s ⁄ p ) gauss = ∑ ci φ ( x, y, λs ⁄ p )i (19) i=1 where N q can assume N s and N p , and c i represents the coupling coefficient between the field of the gaussian input beam and the field of the corresponding i -th mode. Then, the fraction of the total power allocated in each expansion mode for the pumping and for the signal will be: c pi c pi∗ η pi = ------------------------N c si c si∗ η si = -----------------------N c pj c pj∗ c sj c sj∗ p ∑ j=1 s ∑ (20) j=1 615 ER-YB CODOPED WAVEGUIDE AMPLIFIER In this way, for multimode waveguides, the normalized intensity profile for the signals and the pump can be calculated as: Nq i ∑ ηsi ⁄ pi Ψs ⁄ p Ψs ⁄ p = (21) i=1 where i i Ψ s ( x, y ) and Ψ p ( x, y ) are the normalized intensity profiles at the signals and the pump wavelength, respectively. The Refractive index file has the following default format: UPI3DRI 3.0 file header NPMX NPMY number of points in mesh X and mesh Y Xmin Xmax Ymin Ymax minimum and maximum mesh points in X and Y Z1 Number Z data point with coordinates (xmin, ymin) Z2 Number Z data point with coordinates (xmin+dx, ymin) . . . ZN Number Z data point with coordaintes (xmax, ymax) where N is NPMX x NPMY and The sequence of points 616 dx = ( x max – x min ) ⁄ ( NPMX – 1 ) . Z i is ordered in the following way: ER-YB CODOPED WAVEGUIDE AMPLIFIER where the initial point is 0 and the final point is 29. As an example, we have the following waveguide transversal profile: 617 ER-YB CODOPED WAVEGUIDE AMPLIFIER It has the following refractive index file: References: [1] M. Federighi, F. Di Pasquale, "The Effect of Pair-Induced Energy Transfer on the Performance of Silica Waveguide Amplifiers with High Er+3/Yb+3 Concentration", IEEE Photonics Technology Letters, Vol.7, No.3, pp.303-305, March 1995. [2] S. Honkanen, S.I. Najafi e W.J. Wang, "Composite Rare-Earth Doped Glass Waveguides", IEEE Electronics Letters, Vol.28, No.8, pp.746-747, abril, (1992). 618 YB-DOPED FIBER Yb-Doped Fiber This component simulates a bidirectional Ytterbium-doped fiber. The component solves numerically the rate and propagation equations for the steady-state case and can take into account nonlinear phase changes caused by SPM and XPM effects by propagating the signal using the nonlinear Schrödinger equation.. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 5 m — [0,1000000] 0.8 ms — [1e-100,1e100] 3.4 μm — [1,1e100] 3.4 μm — [1,1e100] 1e+025 m-3 m-3, ~ppm-wt, ~wt% [1,1e100] 0.2 1550 nm [0.01, 1] Specifies the doped fiber length. Excited-state lifetime Fluorescence decay lifetime Core radius Specifies the doped fiber core radius Yb doping radius Specifies the doped radius Yb ion density Specifies the Ytterbium doping in the fiber Numerical aperture Specifies the numerical aperture of the fiber 619 YB-DOPED FIBER Cross-sections Name and description Default value Units Value range File frequency unit nm — nm, m, Hz, THz False — True, False Ytterbium.dat — — Determines whether or not the component is enabled OptiAmplifier format Determines if the format of the cross-section file is an OptiAmplifier file Cross-section file name Specifies the Ytterbium cross-section file name Enhanced Name and description Default value Default Unit Units Value range Background loss data type Constant — — Constant, From File 0 dB/km — [0,1e100] Loss.dat — — — False — — True, False 150 dB/km — [0,1e100] Calculate — — Calculate, From file Capture.dat — — Constant, From File False — — True, False Determines if the loss will be calculated from the loss at 1310 nm (constant) or loaded from a data file Loss at 1310 nm Specifies the fiber loss at 1310 nm Background loss file name Specifies the loss file name Include Rayleigh backscattering Determines the inclusion or not of the Rayleigh scattering effect Rayleigh constant Specifies the value of the Rayleigh constant Backscattering capture fraction Determines whether the capture fraction values will be calculated by the component or it will be loaded from a file Rayleigh capture file name Specifies the capture file name Double-clad fiber Specifies if the doped fiber is double-clad 620 YB-DOPED FIBER Name and description Default value Default Unit Units Value range Pump reference 1000 nm — [600,1200] Calculate — — Calculate, From file 3000 μm — [1, 100000] PumpAbsorptio n.dat — — — 300 K — [0,1000] False — — True, False 1060 nm — [600,1700] -33.5 ps/nm/km — [1e-100, 1e100] 0.05 ps/nm2/km — [1e-100, 1e100] Name and description Default value Default Unit Units Value range Include SPM False — — True, False Constant — — Constant, From file If the fiber is double-clad,then reference wavelength that define the pump has to be specified Double-clad data type Specify if the pump multimode aborption will be calculated by using the inner clad area or it will be loaded Cladding area 2 Specifies the inner clad section Pump absorption file name Specifies the pump absorption file Temperature Absolute temperature Include Dispersion Defines whether to include dispersion effects or not Reference wavelength Value of the specified reference wavelength Dispersion Value of dispersion parameter at the reference wavelength Dispersion slope Value of dispersion slope at the reference wavelength Nonlinear effects Determines if the self-phase modulation will be taken into account. If True the optical signal will be propagated using the nonlinear Shrödinger equation. This parameter will also enable Crossphase modulation and Four-wave mixing effects. Effective area data type Defines is the effective area is constant or loaded from a file 621 YB-DOPED FIBER Name and description Default value Default Unit Units Value range Effective area 50 um2 — [1e-100, 1e100] Effective Area.dat — — — Constant — — Constant, From file 2.6e-020 m^2/W — [0,1e100] n2.dat — — — False — — True, False Constant — — Constant, From file 4.6e-011 m/W — Calculate, From file Brillouin.dat — — — 31.7 MHz — [1e-100, 1e100] 11 GHz — [1e-100, 1e100] False — — True, False Raman gain — — Raman gain, Raman gain efficiency Defines value of the effective area Effective area file name Specifies the effective area filename n2 data type Defines if the nonlinear index is constant or loaded from a file n2 Nonlinear index value n2 file name Specifies the nonliner index area filename Include Brillouin scattering Determines if the Brillouin scattering effect will be taken into account Brillouin gain data type Defines if the Brillouin gain is constant or loaded from a file Brillouin gain constant Brillouin gain value Brillouin gain file name Specifies the Brillouin gain file name Brillouin linewidth Specifies the Brillouin linewidth Frequence shift Specifies the Brillouin frequency shift IInclude Raman scattering Determines if the Raman scattering effect will be taken into account Raman gain data type Defines Raman gain type. If Raman gain efficiency is selected then the value in the raman gain file should be Raman gain / Effective area. Otherwise the file contain the normalized Raman gain that will be multiplied by the Raman gain peak 622 YB-DOPED FIBER Name and description Default value Default Unit Units Value range Raman gain peak 1e-013 — — [0, 1e100] 1000 nm — [0, 1e100] Raman Gain.dat — — — 2 — — [1,2] Raman gain peak that will multiply the normalized Raman gain Raman gain reference pump Value used in the Raman gain calculation Raman gain file name Specifies the normalized Raman gain file name or Raman efficiency file name Polarization factor Actual value depends on relative polarization of the fields. The value is 1 if the the fields have aligned polarizations, and two if they have polarization scrambled Numerical Name and description Default value Units Value range Relative error 0.0001 — [1e-100, 1] 150 — [1, 1e8] 100 — [1, 1e8] Calculate — Calculate, LoadFromFile Overlapfactor.dat — — True — — 100 GHz Hz, GHz, THz 0.001 — — Specifies the maximum difference acceptable between two consecutive iterations to complete the iteration process. Max. number of iterations Specifies the maximum number of times for the iteration process. Longitudinal steps Specifies the number of longitudiinal steps in the fiber. Overlap factor data Determines whether the overlap factor values will be calculated by the component or it will be loaded from a file. Overlap factor file name Specifies the overlap factor file name Discretize sampled signal Defines whether to use a user defined discretization for sampled signals or not Frequency resolution Frequency spacing that will discretize the sampled signal Step tolerance Used in the Brillouin calculation and defines tolerance in the definition of length step 623 YB-DOPED FIBER Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Noise Name and description Default value Default units Units Value range Noise center frequency 299.8 THz Hz, THz, nm [30, 30e5] 60 THz Hz, THz, nm ]0, +INF[ 300 THz Hz, GHz, THz, nm [1, 1000] -100 dB — ]-INF, 0[ 3 dB — [0, +INF[ Convert noise bins — — True, False Minimum value for adaptation of noise bins Noise bandwidth Bandwidth to create noise bins Noise bins space Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal. Random numbers Name and description Default value Units Value range Generate random seed True — True, False 0 — [0, 4999] Name and description Default value Units Value range Calculate graphs False — True, False Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs 624 YB-DOPED FIBER Name and description Default value Units Value range Number of distance steps 20 — [1, 1e8] Number of wavelength steps 20 — [1, 1e8] Linear scale True — True, False Minimum value -50 dBm ]1e-100, 1e100[ Pump reference wavelength 1400 nm [100, 1900] 625 YB-DOPED FIBER Technical Background The Ytterbium-Doped Fiber component is based on the solution of the rate and propagation equations of a two-level system. Rate equations are based on energy levels and describe the effects of absorption, stimulated emission, and spontaneous emission on the populations of the lower (n1) and upper (n2) states. For a two-level system with k optical beams the rate equations is given by [1][2]: dn dn – --------1 = --------2 = dt dt σa ( vk ) σe ( vk ) 1 - ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 1 ( r, φ, z ) – ∑ ---------------- ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 2 ( r, φ, z ) – --- ⋅ n 2 ( r, φ, z ) ∑ --------------hvk hv k τ k k n 1 ( r, φ, z ) + n 2 ( r, φ, z ) = n t ( r, φ, z ) (1a) (1b) h is the Planck constant, τ is the excited-state lifetime parameter, v k is the frequency and P k is the power of the kth beam. The absorption and emission crosssection of the kth beam are σ a ( v k ) and σ e ( v k ) , respectively, and n t is the local ytterbium ion density. The normalized optical intensity i k ( r, φ ) is defined as i k ( r, φ ) = I k ( r, φ, z ) ⁄ P k ( z ) , where I k ( r, φ, z ) is light intensity distribution of where the kth beam. The propagation equations describe the propagation of the beams through the doped fiber and are given by: dPk --------- = u k ⋅ σ 3 ( v k ) ⋅ ( P k ( z ) + P0k ) ⋅ dz 2π ∞ ∫ ∫ n2 ( r, φ, z ) ⋅ ik ( r, φ ) ⋅ r ⋅ dr ⋅ dφ – uk ⋅ σa ( vk ) ⋅ Pk ( z ) . 0 0 (2) 2π ∞ ∫ ∫ n2 ( r, φ, z ) ⋅ ik ( r, φ ) ⋅ r ⋅ dr ⋅ dφ 0 0 where each beam propagates in the forward ( u k = 1 ) or backward ( u k = – 1 ) P 0k means the spontaneous emission contribution from the local metastable population n 2 . P 0k = m ⋅ h ⋅ v k ⋅ Δv k , where the normalized number of modes m is normally 2 and Δv k is the noise bandwidth. direction, and 626 YB-DOPED FIBER Setting the time derivative in Equation (1a) to zero and using (1b), the problem is reduced to the steady-state case and the Yb upper-population is defined as: n σa ( vk ) ⋅ τ - ⋅ i k ( r, φ ) ⋅ P k ( z ) ∑ ---------------------hv k k=1 n 2 ( r, φ, z ) = n t ⋅ ------------------------------------------------------------------------------------------------------------n ( σa ( vk ) + σ e ( vk ) ) ⋅ τ - ⋅ i k ( r, φ ) ⋅ P k ( z ) + 1 ∑ ------------------------------------------------hv k (3) k=1 With the specified boundary conditions at z = 0 , (3) can be integrated over space and frequency. Figure 1 L , and z = L , Equations (2) and Example of ytterbium absorption and emission cross-sections It is important realize that the transverse shape of the optical mode and its overlap with the ytterbium ions distribution profile are very important and it can be parameterized by a factor known as overlap integral factor. 627 YB-DOPED FIBER Considering a steady-state case and substituting Equation (1b) in (1a), the rate equation becomes: σa ( vk ) σa ( vk ) σe ( vk ) - ⋅ i k ( r, φ ) ⋅ Pk ( z ) ⋅ n t ( r, σ, z ) – ∑ ---------------- ⋅ i k ( r, φ ) ⋅ P k ( z ) ⋅ n 2 ( r, σ, z ) – ∑ ---------------- ⋅ ik ( r, φ ) ⋅ P k ( z ) ⋅ n 2 ( r, σ, z ) ∑ --------------hv k hv k hv k k k k (4) 1 = --- ⋅ n 2 ( r, σ, z ) τ Integrating Equation (4) over space, 2π ∞ 2 1 --- ⋅ n 2 ( r, φ ) ⋅ π ⋅ b eff = τ ∫ ∫ ik ( r, φ ) ⋅ nt ( r, φ ) ⋅ r ⋅ dr ⋅ dφ σa ( vk ) 0 0 - ⋅ Pk ( z ) ⋅ n t ⋅ ----------------------------------------------------------------------------– ∑ --------------hv k n k t 2π ∞ n σa ( v k ) - ⋅ Pk ( z ) ⋅ n2 . ∑ --------------hv k k=1 2π ∞ ∫ ∫ ik ( r, φ ) ⋅ n2 ( r, φ ) ⋅ r ⋅ dr ⋅ dφ n 0 0 -----------------------------------------------------------------------------– ∑ n2 k=1 where ∫ ∫ ik ( r, φ ) ⋅ n 2 ( r, φ ) ⋅ r ⋅ dr ⋅ dφ σe ( vk ) 0 0 ---------------- ⋅ P ( z ) ⋅ n 2 ⋅ ----------------------------------------------------------------------------hv k n k 2 n i is considered the average density, and is given by: 2π ∞ ∫ ∫ ni ( r, φ ) ⋅ r ⋅ dr ⋅ dφ ni( z ) = and b eff is the equivalent radius of the doped region: ∞ b eff 1 --- ⎛ nt ( r ) ⎞2 - ⋅ r . dr⎟ = ⎜ 2 ∫ ----------⎝ nt( 0 ) ⎠ 0 628 0 0 -----------------------------------------------------2 π ⋅ b eff (5) YB-DOPED FIBER when the ion density population is uniform the effective radius is equal to the doped radius, b . For an effective doped radius A eff = π ⋅ 2 b eff . b eff , the effective cross-sectional area is Then, the overlap integral or confinement factor for the ith level can be defined as: 2π ∞ ∫ ∫ ik ( r, φ ) ⋅ ni ( r, φ ) ⋅ r ⋅ dr ⋅ dφ Γ k, i ( z ) = (6) 0 0 ---------------------------------------------------------------------------- ni If the ytterbium ions are well confined to the center of the optical modes, then and Γ k, 2 are nearly equal and can be replaced with the single constant Γ k . Γ k, 1 Therefore, using the definition of overlap integral, the average population density for level 2 is given by: n σa ( vk ) - ⋅ P k ( z ) ⋅ nt ⋅ Γk ∑ --------------hv k k=1 n 2 ( z ) = --------------------------------------------------------------------------------------------------n σa ( vk ) + σe ( vk ) 1--- ⋅ A + -------------------------------------- ⋅ P k ( z ) ⋅ Γk hv k τ eff ∑ (7) k=1 and the propagation equation becomes: dPk --------- = ( σ e ( v k ) + σa ( v k ) ) ⋅ P k ( z ) ⋅ n 2 ⋅ Γ k – σ a ( v k ) ⋅ P k ( z ) ⋅ n t ⋅ Γ k + P0k ⋅ σ e ( v k ) ⋅ n 2 ⋅ Γ k dz Double-clad fibers 629 (8) YB-DOPED FIBER In case of a double-clad fiber, the pump is launched into the multimode inner clad. Then, the overlapping factor between the pump and the fiber doped area, Γ p , can be calculated, when the pump is spatially homogeneous over the multimode section, by [3]: 2 π ⋅ b eff Γ p = ----------------S clad Where (9) S clad is the inner clad area. To consider a double clad fiber in the simulation, the parameter Double-clad fiber should be True and the pump reference must be specified to define the multimode pump (all signals with wavelength lower than the pump reference will be considered a multimode pump). Otherwise, the user can calculate the overlapping factor and load a file with their values. Background loss and Rayleigh scattering The Background loss and Rayleigh scattering effect can be considered in the ytterbium-fiber model, the equations and parameters used to represent them are similar to the ones shown at the erbium-doped fiber component. For reference, see Erbium-doped fiber component's technical background. 630 YB-DOPED FIBER Cross-section file The cross-section file is specified in an ASCII file with three columns. The first column refers to the wavelength (or frequency) in [m], [nm], [Hz] or [THz] units; the File frequency unit parameter defines the unit of this column. The second column gives the absorption cross-section in [m2] units. The third column gives the emission crosssection file in [m2] units. The unit of the second and third column must be in [m2]. As an example, one possible cross-section file format is: Column A = 2 2 λ [ nm ] , Column B = σ a [ m ] , and Column C = σ e [ m ] . The parameter OptiAmplifier format is used to allow the component load crosssections files originated from the software OptiAmplier. Therefore, if the user wants to load a cross-section under the crs format (format used in the OptAmplifier software), the OptiAmplifier format parameter has to be set TRUE. Background loss and Rayleigh files First, the user can choose the Background loss data type parameter that determines the background loss through the loss at 1310nm (Loss at 1310 nm parameter) or using a wavelength dependent background loss loaded from a file. In the second case, the user has to specify the name of the file containing the losses in the Background loss file name parameter. The format of this file must be similar to the example below: λ [ nm ] α [ dB ⁄ km ] 1460 10 1461 10.5 1462 10.2 1463 10.1 1464 10.3 631 YB-DOPED FIBER The user can include the Rayleigh scattering effect in the simulations through the parameter Include Rayleigh scattering. If the Include Rayleigh scattering parameter is TRUE, then the user has to specify the value of the Rayleigh constant. The Backscattering capture parameter determines if the component will generate the capture fraction using the equation (25) or the user will provide a file with the capture fraction. In this case the user should specify the file name in the Rayleigh capture file name parameter and the file has to be in the format similar to the below: λ [ nm ] C [ dB ] 1460 -20 1461 -21.5 1462 -21 1463 -20.5 1464 -20.48 Overlap factor file In the case of load the overlap factor from a file, the user has to specify the file name in the Overlap factor file name parameter and the file has to in the format as in the example below: λ [ nm ] Γ 1449.91984 0.45 1451.30261 0.44 1452.68537 0.43 1454.06814 0.42 1455.4509 0.41 References: [1] C. Randy Giles, and Emmanuel Desurvire, "Modeling Erbium-Doped Fiber Amplifiers". IEEE Journal of Lightwave Technology, Volume: 9 Issue: 2, Feb. 1991, Page(s): 271 - 283. [2] R. Paschotta, J. Nilsson, A. C. Tropper, and D. C. Hanna, "Ytterbium-Doped Fiber Amplifiers". IEEE Journal of Quantum Electronics, Volume: 33 Issue: 7, Jul. 1997, Page(s): 1049 - 1056. [3] A. Hardy, and H. Oron, "Signal Amplification in Strongly Pumped Fiber Amplifiers". IEEE Journal of Quantum Electronics, Volume: 33 Issue: 3, Mar. 1997, Page(s): 307 - 313. 632 YB-DOPED FIBER DYNAMIC Yb-Doped Fiber Dynamic This component simulates a bidirectional Ytterbium-doped fiber considering the simulation of dynamic effects. The component solves the rate and propagation equations numerically. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Length 5 m [0, 1000000] 0.8 ms [1e-100, 1e100] 3.4 μm [1, 1e100] 3.4 μm [1, 1e100] 1e+025 m-3 Specifies the doped fiber length Excited-state lifetime Fluorescence decay lifetime Core radius Specifies the doped fiber core radius Yb doping radius Specifies the doped radius Yb ion density Specifies the Ytterbium doping in the fiber m-3, ~ppm-wt, ~wt% [1,1e100] 633 YB-DOPED FIBER DYNAMIC Name and description Default value Numerical aperture 0.2 Default unit Units Value range [0.1, 1] Specifies the numerical aperture of the fiber Cross Sections Name and description Default value Units Value range File frequency unit nm [Nm, m, Hz, THz] False [True, False] Determines the frequency unit of the file with the cross sections OptiAmplifier format Determines if the format of the cross-section file is an OptiAmplifier file Cross section file name Ytterbium.dat Specifies the Ytterbium cross section file name Enhanced Name and description Default value Background loss data type Constant Units [Constant, LoadFromFile] Determines if the loss will be calculated from the loss at 1310 nm (constant) or if it will be loaded from a file Loss at 1310 nm 0 Value range dB/Km [0, +INF] Specifies the fiber loss at 1310 nm Background loss file name Loss.dat Specifies the loss file name Include Rayleigh Scattering False [True, False] Determines the inclusion of the Rayleigh scattering effect Rayleigh Constant 150 dB/Km [0, 1000] Specifies the value of the Rayleigh constant Backscattering capture fraction Calculate Determines whether the capture fraction values will be calculated by the component or if it will be loaded from a file Rayleigh capture file name Specifies the capture file name 634 Capture.dat [Calculate, LoadFromFile] YB-DOPED FIBER DYNAMIC Name and description Default value Double-clad fiber False Units Value range [True, False] Specifies if the doped fiber is double-clad Pump reference 1000 nm [600, 1200] 3000 um2 [1, 100000] Name and description Default value Units Value range Relative error 0.0001 [1e-100, 1] 150 [1, 1e8] 100 [1, 1e8] Calculate [Calculate, LoadFromFile] If the fiber is double-clad,then reference wavelength that define the pump has to be specified Cladding area Specifies the inner clad section Numerical Specifies the maximum difference acceptable between two consecutive iterations to finish the iteration process Maximum number of iterations Specifies the maximum number of times for the iteration process Longitudinal steps Specifies the number of longitudinal steps in the fiber Overlap factor data Determines whether the overlap factor values will be calculated by the component or if they will be loaded from a file Overlap factor file name Overlapfactor.dat Specifies the overlap factor file name Reference time 0.5/Bit rate s [1e-100, 1e100] Name and description Default value Units Value range Enabled True Specifies the instant of time used to take the powers in the fiber to solve the steady-state regime Simulation [True, False] Define whether the component is enabled or not 635 YB-DOPED FIBER DYNAMIC Noise Name and description Default value Default unit Units Value range Noise center frequency 299.8 THz Hz, THz, nm [30, 30e5] 60 THz Hz, THz, nm [0, +INF] 300 THz Hz, GHz, THz, nm [1, 1000] -100 dB [-INF, 0] 3 dB [0, +INF] Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins space Specifies the noise bins spacing Noise threshold Minimum value for the adaptation of noise bins Noise dynamic Threshold ratio for the adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Convert noise bins [True, False] Random Numbers Name and description Default value Units Value range Generate random seed True [True, False] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Graphs Name and description Default value Calculate graphs False [True, False] Number of distance steps 20 [1, 1e8] Number of wavelength steps 20 [1, 1e8] Linear scale True [True, False] Minimum value -50 dBm [1e-100, 1e100] Pump reference wavelength 1400 nm [100, 1900] 636 Units Value range YB-DOPED FIBER DYNAMIC Technical Background The Ytterbium-Doped Fiber Dynamic component is based on the solution of the simplified two-level rate and propagation equations. Rate equations are based on energy levels and describe the effects of absorption, stimulated emission, and spontaneous emission on the populations of the lower (n1) and upper (n2) states. For the two-level system with k optical beams, the rate equations are given by [1][2] where h is the Planck constant τ is the excited-state lifetime parameter vk is the frequency Pk is the power of the kth beam. σ a ( v k ) is the absorption cross-section of the kth beam σ e ( v k ) is the emission cross-section of the kth beam nt is the local ytterbium ion density The normalized optical intensity, i k (r,φ) , is defined as i k (r,φ) = ( I k (r, φ,z) ) ⁄ ( P k ( z ) ) where I k (r, φ,z) is the light intensity distribution of the kth beam The propagation equations describe the propagation of the beams through the doped fiber and are given by 637 YB-DOPED FIBER DYNAMIC where each beam propagates in the forward direction ( u k = 1 ) or the backward direction( u k = – 1 ), and P 0k means the spontaneous emission contribution from the local metastable population n 2 . P 0k = m ⋅ h ⋅ v k ⋅ Δv k where m is the normalized number of modes and is normally 2 Δv k is the noise bandwidth With the specified boundary conditions at z = 0 and (2) can be integrated over space and frequency. Figure 1 z = L , the equations (1) and An example of Ytterbium absorption and emission cross sections Double-clad Fibers In case of a double-clad fiber, the pump is launched into the multimode inner clad. Then, the overlapping factor between the pump and the fiber doped area, Γ p , can be calculated when the pump is spatially homogeneous over the multimode section, by [3] 638 YB-DOPED FIBER DYNAMIC where Sclad is the inner clad area To consider a double-clad fiber in the simulation, the parameter Double-clad fiber must be True and the pump reference must be specified to define the multimode pump. All signals with a wavelength lower than the pump reference will be considered a multimode pump. Otherwise, the user can calculate the overlapping factor and load a file with their values. Background loss and Rayleigh Scattering The Background loss and Rayleigh scattering effect can be considered in the Ytterbium-fiber model. The equations and parameters used to represent them are similar to the ones shown in the erbium-doped fiber component. For reference, see the Erbium-doped fiber component's technical background. Cross-section file The cross-section file is specified in an ASCII file with three columns. The first column refers to the wavelength (or frequency) in m, nm, Hz or THz units. The File frequency unit parameter defines the units of this column. The second column gives the absorption cross-section in m2 units. The third column gives the emission cross-section file in m2 units. The unit of the second and third column must be in m2. As an example, one possible cross-section file format is: 639 YB-DOPED FIBER DYNAMIC The parameter OptiAmplifier format is used to allow the component to load crosssections files originated from the software OptiAmplier. Therefore, if the user wants to load a cross-section under the crs format (format used in the OptAmplifier software), the OptiAmplifier format parameter has to be set TRUE. Background loss and Rayleigh files First, the user can choose the Background loss data type parameter. This parameter determines the background loss through the loss at 1310 nm (Loss at 1310 nm parameter) or by using a wavelength dependent background loss loaded from a file. In the second case, the user has to specify the name of the file that contains the losses in the Background loss file name parameter. The format of this file must be similar to the example below. The user can choose to include the Rayleigh scattering effect in the simulations through the parameter Include Rayleigh scattering. If the Include Rayleigh scattering parameter is TRUE, the user has to specify the value of the Rayleigh constant. The Backscattering capture parameter determines if the component will generate the capture fraction using the equation (25) or if the user will provide a file with the capture fraction. In the latter case, the user should specify the file name in the Rayleigh capture file name parameter and the file has to be in the format similar to the example below: Overlap factor file In the case of loading the overlap factor from a file, the user has to specify the file name in the Overlap factor file name parameter and the file has to in the format as shown in the example below: 640 YB-DOPED FIBER DYNAMIC References [1] C. Randy Giles, and Emmanuel Desurvire, "Modeling Erbium-Doped Fiber Amplifiers". IEEE Journal of Lightwave Technology, Volume: 9 Issue: 2, Feb. 1991, Page(s): 271 - 283. [2] R. Paschotta, J. Nilsson, A. C. Tropper, and D. C. Hanna, "Ytterbium-Doped Fiber Amplifiers". IEEE Journal of Quantum Electronics, Volume: 33 Issue: 7, Jul. 1997, Page(s): 1049 - 1056. [3] A. Hardy, and H. Oron, "Signal Amplification in Strongly Pumped Fiber Amplifiers". IEEE Journal of Quantum Electronics, Volume: 33 Issue: 3, Mar. 1997, Page(s): 307 - 313. 641 YB-DOPED FIBER DYNAMIC Notes: 642 TRAVELING WAVE SOA Traveling Wave SOA Performs lumped amplification with traveling wave semiconductor optical amplifiers (SOA). The rateequation approximation has been used in which the electrical field is described by the wave equation and the carrier density by means of the rate equation. Such model is applicable to describe the amplification of CW and optical pulsed signals. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Injection current 0.15 A [0,1] Name and description Default value Units Value range Length 0.0005 m ]0,1e-3] Width 3e-006 m ]0,500e-6] Height 8e-008 m ]0,10e-6] Optical confinement factor 0.15 — ]0,1] Loss 4000 1/m [0,10e-4] Differential gain 2.78e-020 m2 ]0,50e-20] Carrier density at transparency 1.4e+024 m3 ]0,10e-25] Linewidth enhancement factor 5 — [–30,30] Recombination coefficient A 143e+008 1/s ]0,1e-15] Physical 643 TRAVELING WAVE SOA Name and description Default value Units Value range Recombination coefficient B 1e-016 m3/s ]0,1e-10] Recombination coefficient C 3e-041 m6/s [0,1e-30] Initial carrier density 3e+024 m–3 ]0,10e-25] Numerical Name and description Value Units Mode Integration type Runge Kutta 4th order — Normal Relative tolerance 1e-006 — Normal Maximum number of steps 100000 — Normal Interpolation type Polynomial — Normal Order of polynomial 4 — Normal Name and description Default value Units Value range Enabled True — True, False] Simulation Determines whether or not the component is enabled Technical background This module performs lumped amplification with traveling wave semiconductor optical amplifiers (SOA) [AGR, 1993] and [SHI, 1994]. The rate-equation approximation has been used in which the electrical field is described by the wave equation and the carrier density by means of the rate equation [1-4]. Such model is applicable to describe the amplification of CW and optical pulse signals. The pulse widths have to be much larger than the intraband relaxation time that governs the dynamics of the induced polarization. Typically, the intraband relaxation time is 0.1 ps. Therefore, the model can be used for pulse widths larger than 1 ps [3-4]. The basic approximation done in the wave equation for the electrical field in the SOA is a linear dependence between the carrier induced susceptibility and the carrier density [6-8]. In the framework of this approximation the material gain coefficient gm is related to carrier density N(t) by, gm ( t ) = A g [ N ( t ) – N0 ] (1) where N0 is the carrier density at transparency point and Ag is the differential gain coefficient [2]. 644 TRAVELING WAVE SOA The net gain coefficient g is related to the material gain gm by, g ( t ) = Γgm ( t ) – α (2) where α is an effective loss coefficient which includes scattering and absorption losses and Γ is the optical confinement factor defined as a fraction of the mode power within the active layer. It is also assumed that the amplifier supports a single wave-guide mode and it does not change the polarization state during the amplification. Linearly polarized input light is presumed. The group velocity dispersion in the SOA is neglected. The amplified spontaneous emission noise is not taken into account. In the framework of these assumptions, the gain G for a traveling wave SOA for a distance z is: G ( t ,z ) = e [ g ( t )z ] (3) The carrier density rate equation expresses the conservation of carriers inside the active layer. It takes into account the current density and the net rate of carrier generation and recombination averaged over the active layer. The recombination rate consists of spontaneous and stimulated recombinations. The spontaneous recombination rate includes the radiative and nonradiative components. The nonradiative recombination takes into account the Auger recombination, which is generally the dominant nonradiative process in long wavelength lasers. The spontaneous recombination rate can be characterized by a quantity known as the carrier lifetime τ s : N ( t ) = R N ( t ) + R N 2 ( t ) + R N3 ( t ) ---------A B c τs (4) where RA is the non-radiative coefficient due to recombination at defects and traps, RB is the spontaneous radiative recombination coefficient, and RC is the Auger recombination coefficient. Neglecting the carrier diffusion, the amplified spontaneous emission noise and the shot noise the equation for the carrier density N(t) is [3-4]: dN J N I ------- = ------ – ----A g ( N – N 0 ) ----dt qd τ s hf (5) where I is the light intensity, J is the injection current density, q is the electron charge, h is the Planck’s constant, f is the light frequency, t is the time, and d is the active layer thickness. Equation 5 can be rewritten as: (6) 645 TRAVELING WAVE SOA Ip N dN P ( N ,t )L ------- = ------ – ---- – ΓA g ( N ( t ) – N 0 ) -------------------dt Vhf qV τ s where Ip is the pump current (or injection current), V = L w d is the volume of the active region, and L and w are the length and the width of the amplifier respectively. The amplifier power P(N,t), which is the average power over the length of the amplifier, is by: L P ( N ,z )- dz = P ( N ,t ) = ∫ ---------------L 0 L [ g ( t )L ] P in G ( t ,z ) e---------------------– 1= P ---------------------in ∫ L g(t ) 0 (7) The output optical field is: Eout ( t ) = E in ( t )e [ ( 1 + jδ )g ( t )L ] -----------------------------2 (8) where δ is the linewidth enhancement factor. This parameter takes into account the coupling between the gain and refractive index of the amplifying medium. The output power to parameterized signals is: P out = P in e [ g ( t )L ] (9) To include multiple frequency bands, the term P(N,t) / f in Equation 6 should be substituted with: P k ( N ,t ) ∑ ----------------fk k (10) where fk is the center frequency for each frequency band. Basic physical effects described by the model for single wavelength channel are gain saturation, gain-saturation induced self-phase modulation, and gain recovery [3-5]. Gain-saturation induced self-phase modulation is responsible for important changes in the spectrum of amplified pulses: 646 • appearance of multi-peak spectral structure • red shift of the spectrum TRAVELING WAVE SOA • appearance of the positive chirp In addition, the shape and the spectral pulse distortions depend on the shape and the initial frequency pulse modulation. Gain saturation and gain recovery effects for Gaussian, super Gaussian, and chirped Gaussian pulses for an SOA are in OptiSystem Tutorials — Introduction to the basic gain saturation and gain recovery characteristics of the SOA. A strong agreement with [3-4] can be identified in this section. Generally, gain saturation effect is a serious obstacle for an SOA as an inline amplifier. In the case of single-channel transmission, gain saturation effect leads to a pattern effect. Pattern effect is demonstrated for 10 Gb/s average soliton transmission over a 500 km SMF optical link in OptiSystem Tutorials — Basic application of the OSA as an inline amplifier. In the case of multi-channel transmission, gain saturation effect leads to inter-channel crosstalk. Independent of the problems connected with applying an SOA as an inline amplifier, they are used near the 1.3 μm wavelength in SMF. The fundamental reason for this is the possibility of avoiding the large group velocity dispersion of SMF at 1.55 μm [6-11]. This idea following [11] is demonstrated in OptiSystem Tutorials — Basic application of the OSA as an inline amplifier. Some undesirable properties of applying an SOA as an inline amplifier have found other applications. For example, the positive pulse chirp created during the process of amplification can be used for pulse compression if you can propagate the pulse in a dispersive media with a proper sign of the group velocity dispersion. Pulse compression with the help of SMF following [12] is described in OptiSystem Tutorials — Applying the gain saturation properties of the SOA to obtain pulse compression. SOAs have found new applications as wavelength converters, fast switches for wavelength routing in WDM networks, and nonlinear elements for clock recovery and demultiplexing in TDM systems [5, 13-14]. In OptiSystem Tutorials — Application of the SOA as a wavelength converter, SOA wavelength conversion is demonstrated based on four-wave mixing and cross-saturation effects. References [1] M.J. Adams, H.J. Westlake, M.J. O’Mahony, I.D. Henning, “A Comparison of Active and Passive Optical Bistability in Semiconductors”, IEEE Journal of Quantum Electronics, Vol. QE21, N 9, September 1985. [2] M.J. O’Mahoney, “Semiconductor Laser Optical Amplifier for use in Fiber Systems,” Journal of Lightwave Technology, Vol. 6, N 4, April 1988. [3] G.P. Agrawal and N.A. Olsson, “Self-Phase Modulation and Spectral Broadening of optical pulses in semiconductor Laser Amplifiers”, IEEE J. of Quantum Electronics, Vol. QE-25, N 11, pp. 2297-2306, November 1989. [4] N.A. Olsson and G.P. Agrawal, “Spectral shift and distortion due to self-phase modulation of picosecond pulses in 1.5 mm optical amplifiers”, Appl. Phys. Lett. 55, N 1, pp. 13-15, July 1989. 647 TRAVELING WAVE SOA [5] G.P. Agrawal, “Fiber-Optic Communication Systems”, Second edition, John Wiley & Sons, Inc. 1997. [6] J.J. Reid, C.T.H.F. Liendenbaum, L.F. Tiemeijer, A.J. Boot, P.I. Kuindersma, I. Gabitov, and A. Mattheus, in Proceedings of the 20th European Conference on Optical Communication (Instituto Internationale delle Communicaziono, Genova, Italy, 1994). [7] A. Mecozzi, “Optics Letters,” 20, 1616-1618, 1995. [8] S. Wabnitz, “Optics Letters,” 20, 1979-1982, 1995. [9] S.K. Turitsyn, Phys. Rev. E 54, R3125, 1996. [10] I.M. Uzunov, M. Golles, and F. Lederer, “Optics Letters,” 22, 1406-1408, 1997. [11] M. Settembre, F. Matera, V. Hagele, I. Gabitov, A.W. Mattheus, and S. Turitsyn, “Journal of Lightwave Technology,” Vol. 15, pp. 962-967, 1997. [12] G.P. Agrawal and N.A. Olsson, “Optics Letters,” 14, 500-502, 1989. [13] T. Durhuus, B. Mikkelsen, and K.E. Stubkjaer, “Journal of Lightwave Technology,” Vol. 10, pp. 1056-1065, 1992. [14] T. Durhuus, B. Mikkelsen, C. Joergensen, S.L. Danielsen, and K.E. Stubkjaer, “Journal of Lighwave Technology,” Vol. 14, pp. 942-954, 1992. Technical references [AGR, 1993] G.P. Agrawal and N.K. Dutta, “Semiconductor lasers,” Second edition, International Thomson Publishing, Inc., 1993. [BAS, 1992] S.P. Bastien, H. R. D. Sunak, B. Sridhar, V. E. Kalomiris “Temporal, spatial and spectral modeling of erbium doped fiber amplifiers”, SPIE – Physic and Simulations of Optoelectronic Devices, pp. 2-11, 1992 [BUR, 1998] J. Burgmeier, A. Cords, R. März, C. Schäffer, B. Stummer “A black box model of EDFA’s operating in WDM systems”, Journal of LIghtwave Technology, Vol. 16, N. 7, pp. 1271-1275, 1998 [DES, 1994] E. Desurvire, “Erbium-Doped Fiber Amplifiers – Principles and Applications”, John Wiley & Sons, Inc., USA, 1994 [GIL, 1991] C.R. Giles, E. Desurvire, "Modeling erbium-doped fiber amplifiers," Journal of LIghtwave Technology, Vol. 9, N. 2, pp. 271-283, 1991 [KAR, 1998] J. A. Vallés, “Analysis of channel addition/removal response in all-optical gain-controlled cascade of erbium-doped fiber amplifiers”, Journal of Lightwave Technology, Vol. 16, N. 10, pp. 1795-1803, 1998 [OKO, 1990] T. Okoshi, "Exact Noise-Figure Formulas for Optical Amplifiers and Amplifier-Fiber Cascaded Chains," IEEE/OSA Topical Meeting on Optical Amplifiers and their Applications, Monterrey, PDP11, 1990 [SHI, 1994] S. Shimada, H. Ishio, “Optical Amplifiers and their Applications”, John Wiley & Sons, Chichester, 1994. 648 WIDEBAND TRAVELING WAVE SOA Wideband Traveling Wave SOA The component simulates a traveling wave SOA based on a homogeneous buried ridge stripe SOA. Ports Name and description Port type Signal type Input 1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical Parameters Main Name and description Symbol Default value Units Value range Injection current l 0.13 A [0, 10] Input coupling loss 3 dB [0, 100] Output coupling loss η IN ηo 3 dB [0, 100] Input facet reflectivity R1 5e-5 [0, 5e-3] Output facet reflectivity R2 5e-5 [0, 5e-3] Name and description Symbol Default value Units Value range Length L 700e-6 m [1e-8, 1e-2] Physical Active region length Cross-section data False True, False Defines whether the use will enter the dimensions or the active area of the device directly 649 WIDEBAND TRAVELING WAVE SOA Name and description Symbol Default value Units Value range Width w 0.4e-6 m [1e-8, 1e-2] h 0.4e-6 m [1e-8, 1e-2] 1.6e-013 m^2 [1e-16, 0.01] Active region width Height Active region thickness Active Area The device’s active area Optical confinement factor Γ 0.45 Recombination coefficient A A 360000000 1/s [0, 1e15] B 5.6e-016 m^3/s [0, 1e-10] C 3e-041 m^6/s [1e5, 3e8] Group velocity Vg 75000000 m/s [1e5, 3e8] Temperature T 300 K [0, 1e3] Symbol Default value Units Value range [0, 1] Linear recombination coefficient Recombination coefficient B Bimolecular recombination coefficient Recombination coefficient C Auger recombination coefficient Absolute temperature Enhanced Name and description Material gain No approximation Linear, Lorentzian, No approximation Define if the material gain coefficient is calculated based on reference [1], a linear or Lorentzian approximation. Gain constant ao 2.78e-20 m^2 ]0, 100e-20] 2.9e-32 m^4 ]0, 50e-10] 1.4e24 m^-3 ]0, 10e25] 1605 nm [1000, 1800] Differential gain coefficient Gain constant a2 Gain constant characterizing the gainpeak shift Carrier density at transparency nt Linear radiative recombination coefficient Gain peak wavelength Peak wavelength at transparency 650 λt WIDEBAND TRAVELING WAVE SOA Name and description Symbol Default value Units Value range Gain bandwidth Δλ 122.5 nm [1, 800] me 4.1e-032 kg [0, 1e-10] mhh 4.19e-031 kg [0, 1e-10] mhl 5.06e-032 kg [0, 1e-10] Arad 10000000 1/s [0, 1e15] Brad 5e-16 m^-3/s [0, 1e-10] Active refractive index n1 3.22 dn1/dn dnr -1.8e-026 neq 3.22 dneg -1.8e-026 m^-3 [0, 1e50] kg 9e-011 eVm [0, 1] Eg0 0.77725 eV [0, 1e-3] Ko 6200 m^-1 [0, 1e10] The 3 dB bandwidth of the linear gain coefficient me Effective mass of electron in the conduction band mhh Effective mass of a heavy hole in the valence band mhl Effective mass of a light hole in the valence band Arad Linear radiative recombination coefficient Brad Bimolecular radiative recombination coefficient [1, 10] m^-3 [0, 1e50] Differential of active refractive index with respect to carrier density neq0 [1, 10] Equivalent effective refractive index at zero carrier density dneq/dn Differential of equivalent refractive index at zero carrier density Kg Bandgap shrinkage coefficient Eg0 Bandgap energy with no injected carrier Ko Carrier independent absorption loss coefficient 651 WIDEBAND TRAVELING WAVE SOA Name and description Symbol Default value Units Value range K1 K1 7.5e-021 m^2 [0, 1e25] Name and description Default value Units Value range Numerical model Dynamic Dynamic, Static 0.0001 [1e-100, 1] 150 [1, 1e8] 10 [1, 1e8] False [True, False] Carrier dependent absorption loss coefficient Numerical Defines whether the device will use a Dynamic or Static algorithm to process the input signals Relative error Specifies the maximum difference acceptable between two consecutive iterations to finish the iteration process Max. number of iterations Specifies the maximum number of times for the iteration process Longitudinal steps Specifies the number of longitudinal steps in the fiber Resample input signals Specifies if the electrical and optical input signals should be resampled in accordance with Δt = Δz/vg Simulation Name and description Default value Enabled True Units Value range [True, False] Defines whether the component is enabled or not Noise Name and description Default value Default unit Units Value range Noise center frequency 193.4 THz Hz, THz, nm [30, 30e5] 10 THz Hz, THz, nm [0, +INF] 125 THz Hz, GHz, THz, nm [1, 1000] Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins Noise bins space Specifies the noise bins spacing 652 WIDEBAND TRAVELING WAVE SOA Name and description Default value Default unit Units Value range Noise threshold -100 dB [0, +INF] 3 dB [0, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Convert noise bins [True, False] Random Numbers Name and description Default value Units Value range Generate random seed True [True, False] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The component simulates a traveling wave wideband semiconductor optical amplifier model [1]. This SOA model is based on the numerical solution of a set of coupled differential equations that describe the interaction between the carrier density and photon rates. The traveling-wave equations for the signal fields are described by + dEsk ( z ) + --------------------- = ⎛ – j ⋅ β k + 1--- ( Γ ⋅ g m ( v k, n ) – α ( n ) )⎞ ⋅ E sk ( z ) ⎝ ⎠ dz 2 (1) – dEsk ( z ) – 1 ----------------- = ⎛⎝ j ⋅ β k – --- ( Γ ⋅ g m ( v k, n ) – α ( n ) )⎞⎠ ⋅ E sk ( z ) dz 2 (2) 653 WIDEBAND TRAVELING WAVE SOA where E+sk is a complex traveling wave, propagating in the positive z direction E-sk is a complex traveling wave, propagating in the negative z direction z lies along the amplifier axis with its origin at the input face βk is the propagation coefficient α is the material loss coefficient g m (v k,n) is the material gain coefficient Γ is the optical confinement factor The signal amplification also depends on the amount of spontaneously emitted noise from the amplifier. The traveling wave equations for the spontaneous emission are given by + dN j ( z ) + ---------------------- = ( Γ ⋅ g m ( v j, n ) – α ( n ) ) ⋅ N j ( z ) + Rsp ( v j, n ) dz – dN j ( z ) – ------------------ = – ( Γ ⋅ g m ( v k, n ) – α ( n ) ) ⋅ N j ( z ) + Rsp ( v j, n ) dz (3) (4) where N+ j is the spontaneous emission photon rate traveling in the positive z direction N -j is the spontaneous emission photon rate traveling in the negative z direction Rsp is the emission noise coupled into N+j and N-j The carrier density rate equation expresses the conservation of carriers inside the active layer. It takes into account the current density and the net rate of carrier generation and recombination averaged over the active layer. The recombination rate includes the radiative and nonradiative components. The nonradiative components take into account the Auger recombination, which is generally the dominant nonradiative process in long wavelength lasers. 654 WIDEBAND TRAVELING WAVE SOA The carrier density at z obeys the rate equation dn ( z -) = --------------------------I Γ -⋅⎧ – R ( n ( z ) ) – ---------------------⎨ dt q⋅d⋅L⋅W d⋅W ⎩ ⎧ –⎨ ⎩ N k=1 Nm – 1 ∑ g m ( v j, n ( z ) ) ⋅ ( N j j=1 + ∑ gm ( vk, n ( z ) ) ( Nsk + ⎫ – ( z ) + N sk ( z ) ) ⎬ ⎭ ⎫ – ( z ) + Nj ( z ) ) ⎬ ⎭ (5) where I is the injected bias current R is the recombination rate term q is the electronic charge Ns is the number of signals injected in the SOA. N+sk is the photon rate of the wave in that direction N-sk is the photon rate of the wave in that direction Initially, equations 1 to 5 are solved numerically by splitting the amplifier into a number of sections and considering the steady state condition (the numerical algorithm presented in [1] is used). After the step above the time evolution of carrier density rate will depend only on current bias level and the input fluxes in each section of the SOA. The material gain is calculated based on definition chose at the Material gain parameter in accordance with [1] 2 2 ⋅ m e ⋅ m hh c ⎞ g m ( v, n ) = ----------------------------------------------------- ⋅ ⎛⎝ -------------------------------------------------⎠ 3⁄2 2 2 h/ ( 2 ⋅ π ) m ⋅ ( ⋅ m ) e hh 4 ⋅ 2 ⋅ π n1 ⋅ τ ⋅ v Where c is the light speed constant, h is the Planck constant and recombination lifetime. (6) τ is the radiative Linear - The material gain is calculated based on the linear approximation (See Traveling Wave SOA component technical description). 655 WIDEBAND TRAVELING WAVE SOA Lorentzian - The material gain is calculated as having a Lorentzian lineshape [2]: a 0 ⋅ ( n – nt ) g m ( v, n ) = -------------------------------2 ( λ – λN ) 1 + ---------------------2 Δλ Where (7) λ N is the spectral shift given by: λ N = λ t – a 2 ⋅ ( n – nt ) (8) References [1] Michael J. Connelly, "Wideband Semiconductor Optical Amplifier Steady-State Numerical Model". IEEE Journal of Quantum Electonics, vol. 37, no. 3. March 2001. [2] Mourad Menif, Pascal Lemieux, Walid Mathlouthi and Leslie Ann Rusch, " Incoherent-toCoherent Wavelength Conversion Using Semiconductor Optical Amplifier" . IEEE International Conference on Communications (ICC) 2004. 656 REFLECTIVE SOA Reflective SOA The component simulates a reflective semiconductor optical amplifier including the dynamic dependence between electric and optical input signals. Ports Name and description Port type Signal type Electrical Input Input Electrical Electrical Output Output Electrical Input 1 Input Optical Output 1 Output Optical Input 2 Input Optical Output 2 Output Optical Parameters Main Name and description Symbol Default value Units Value range Input coupling loss η IN 3 dB [0, 100] Output coupling loss ηo 3 dB [0, 100] Input facet reflectivity R1 5e-5 [0, 5e-3] Output facet reflectivity R2 5e-5 [0, 5e-3] Name and description Symbol Default value Units Value range Active length L 700e-6 m [1e-8, 1e-2] 700e-6 m [1e-8, 1e-2] Physical Active region length Taper length Taper region length 657 REFLECTIVE SOA Name and description Symbol Cross-section data Default value Units False Value range [True, False] Defines whether the user will enter the cross-section dimensions or the active area of the device Width w 0.4e-6 m [1e-8, 1e-2] h 0.4e-6 m [1e-8, 1e-2] Aeff 1.6e-13 m^2 [1e-18,0.01] Optical confinement factor Γ 0.45 Recombination coefficient A A 360000000 1/s [0, 1e15] B 5.6e-016 m^3/s [0, 1e-10] C 3e-041 m^6/s [1e5, 3e8] Group velocity Vg 75000000 m/s [1e5, 3e8] Temperature T 300 K [0, 1e3] T 2 Symbol Default value Units Value range No approximation kg No approximation, Linear, Lorentzian a0 2.5e-20 m^2 ]0,100e-20] a2 2.9e-32 m^4 ]0,50-10] Active region width Height Active region thickness Active area The cross section area of the active layer [0, 1] Linear recombination coefficient Recombination coefficient B Bimolecular recombination coefficient Recombination coefficient C Auger recombination coefficient Absolute temperature Junction ideality factor [0, 100] Enhanced Name and description Material gain Define if the material gain coefficient is calculated based on reference [1], linear or Lorentzian approximation Gain constant ao Differential gain coefficient Gain constant a2 Gain constant characterizing the gainpeak shift 658 REFLECTIVE SOA Name and description Symbol Default value Units Value range Carrier density at transparency nt 1.4e24 m^-3 ]0, 10e25] εnl 1.2e-22 m^3 ]0, 100e-15] λt 1639 nm [1000,1800] Δλ 122.5 nm [1,800] me 4.1e-032 kg [0, 1e-10] mhh 4.19e-031 kg [0, 1e-10] mhl 5.06e-032 kg [0, 1e-10] Arad 10000000 1/s [0, 1e15] Brad 5e-16 m^3/s [0, 1e-10] Active refractive index n1 3.22 dn1/dn dnr -1.8e-026 neq 3.22 dneg -1.8e-026 m^-3 [0, 1e50] kg 9e-011 eVm [0, 1] Transparent carrier density Nonlinear gain parameter Equivalent effective refractive index at zero carrier density Gain peak wavelength Peak wavelength at transparency Gain bandwidth The 3 dB bandwidth of the linear gain coefficient me Effective mass of electron in the conduction band mhh Effective mass of a heavy hole in the valence band mhl Effective mass of a light hole in the valence band Arad Linear radiative recombination coefficient Brad Bimolecular radiative recombination coefficient [1, 10] m^-3 [0, 1e50] Differential of active refractive index with respect to carrier density neq0 [1, 10] Equivalent effective refractive index at zero carrier density dneq/dn Differential of equivalent refractive index at zero carrier density Kg Bandgap shrinkage coefficient 659 REFLECTIVE SOA Name and description Symbol Default value Units Value range Eg0 Eg0 0.77725 eV [0, 1e-3] Ko 6200 m^-1 [0, 1e10] K1 7.5e-021 m^2 [0, 1e25] Name and description Default value Units Relative error 0.0001 [1e-100, 1] 150 [1, 1e8] 10 [1, 1e8] False [True, False] Bandgap energy with no injected carrier Ko Carrier independent absorption loss coefficient K1 Carrier dependent absorption loss coefficient Numerical Value range Specifies the maximum difference acceptable between two consecutive iterations to finish the iteration process Max. number of iterations Specifies the maximum number of times for the iteration process Longitudinal steps Specifies the number of longitudinal steps in the fiber Resample input signals Specifies if the electrical and optical input signals should be resampled in accordance with Δt = Δz/vg Simulation Name and description Default value Enabled True Units Value range [True, False] Defines whether the component is enabled or not Noise Name and description Default value Default unit Units Value range Noise center frequency 299.8 THz Hz, THz, nm [30, 30e5] 60 THz Hz, THz, nm [0, +INF] Determines the noise center frequency Noise bandwidth Bandwidth to create noise bins 660 REFLECTIVE SOA Name and description Default value Default unit Units Value range Noise bins space 300 THz Hz, GHz, THz, nm [1, 1000] -100 dB [0, +INF] 3 dB [0, +INF] Specifies the noise bins spacing Noise threshold Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Convert noise bins Determines if the generated noise bins are incorporated into the signal Convert noise bins [True, False] Random Numbers Name and description Default value Units Value range Generate random seed True [True, False] 0 [0, 4999] Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical Background The component simulates a reflective semiconductor optical amplifier (RSOA) model with bulk material as the active element [1]. This SOA model is based on the numerical solution of a set of coupled differential equations that describe the interaction between the carrier density and photon rates along the active layer length. The rate and propagation equations solved in this model are similar to the ones described in the Wideband Traveling Wave SOA technical background, however the value of the injection current here is considered as an input signal allowing the modulation of the optical signal by the SOA. This component also considers the possibility of sensing the differences in voltage produced at the bias electrode of the single-section SOA. In this case the voltage variation is defined by the following equation [2]: K B T N bias ( z ) + N ( z ) ln -------------------------------------Vφ = η j ---------e N bias ( z ) (1) 661 REFLECTIVE SOA References [1] Michael J. Connelly, "Wideband Semiconductor Optical Amplifier Steady-State Numerical Model". IEEE Journal of Quantum Electonics, vol. 37, no. 3. March 2001. [2] Thierry Rampone, Hong-Wu Li, and Ammar Sharaiha. "Semiconductor Optical Amplifier Used as an In-Line Detector with the Signal DC-Component Conservation". IEEE Journal of Lightwave Technology, vol. 16, no. 7. July 1998. 662 LIMITING AMPLIFIER Limiting Amplifier This component is an electrical limiting amplifier. The minimum and maximum output signal values are user-defined parameters. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Units Value range Max. output voltage 0.5 Volt ]INF,+INF[ -0.5 Volt ]INF,+INF[ Name and description Default value Units Value range Enabled True — The maximum value of the output signal. Min. output voltage The minimum value of the output signal. Simulation Determines whether or not the component is enabled 663 LIMITING AMPLIFIER Technical background This component measures the input signals and compares the amplitude with the parameters Max. output voltage and Min. output voltage. If the signal value is outside of the range between the min and max values, the signal will be clipped. This component does not affect the noise amplitude, only the signal amplitude. 664 ELECTRICAL AMPLIFIER Electrical Amplifier Electrical amplifier with additive thermal noise. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Units Value range Gain 10 dB [-1e+100, 1e+100] Include noise Yes — — PSD Yes — — –60 dBm W, mW, dBm Name and description Default value Units Value range Enabled True — Determines whether the power is defined as PSD or the average power in time Noise power Value of the PSD or the average power Simulation Determines whether or not the component is enabled 665 ELECTRICAL AMPLIFIER Noise Name and description Default value Default unit Units Value range Include noise Yes — — Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 666 TRANSIMPEDANCE AMPLIFIER Transimpedance Amplifier This component is an electrical transimpedance amplifier with user defined noise figure. It has linear gain and additive thermal noise. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Units Value range Voltage gain 600 Ohm, kOhm, dB [0,+INF[ True — True, false 0.8 * Bit rate Hz, MHz, GHz [0,+INF] 6 dB [0,+INF] 4e-21 A/Hz-1, W/Hz, mW/Hz, dBm/Hz [0,+INF] The linear gain of the amplifier. Include Noise Defines whether the noise will included in the output Noise equivalent bandwidth Frequency range of the noise power Noise figure Amplifier noise figure Input noise density Minimum input noise 667 TRANSIMPEDANCE AMPLIFIER Simulation Name and description Default value Units Enabled True — Value range Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Include noise Yes — — PSD Yes — — –60 dBm W, mW, dBm No — — Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines whether the power is defined as PSD or the average power in time Noise power Value of the PSD or the average power Add noise to signal [-1e+100, 1e+100] Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background This component amplifies the input electrical signal and adds thermal noise to the signal output. The value of the thermal noise is calculated from the input SNR and the user defined parameter Noise figure. Since OptiSystem can have noiseless electrical signals, the parameter Input noise density assures a minimum value for the noise floor at the input signal. 668 AGC AMPLIFIER AGC Amplifier This component is an electrical limiting amplifier with user defined noise figure. It has signal dependent gain and additive thermal noise. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Units Value range Output voltage 0.005 Volt [0,+INF[ False — True, false 0.8 * Bit rate Hz, MHz, GHz [0,+INF] 6 dB [0,+INF] 4e-21 A/Hz-1, W/Hz, mW/Hz, dBm/Hz [0,+INF] The peak value of the output signal. Include Noise Defines whether the noise will included in the output Noise equivalent bandwidth Frequency range of the noise power Noise figure Amplifier noise figure Input noise density Minimum input noise 669 AGC AMPLIFIER Simulation Name and description Default value Units Enabled True — Value range Determines whether or not the component is enabled Noise Name and description Default value Default unit Units Value range Include noise Yes — — PSD Yes — — –60 dBm W, mW, dBm No — — Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines whether the power is defined as PSD or the average power in time Noise power Value of the PSD or the average power Add noise to signal [-1e+100, 1e+100] Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation Technical background This component amplifies/attenuates the input electrical signal and adds thermal noise to the signal output. The output signal will have a peak value defined by the parameter Output voltage. The value of the thermal noise is calculated from the input SNR and the user defined parameter Noise figure. Since OptiSystem can have noiseless electrical signals, the parameter Input noise density assures a minimum value for the noise floor at the input signal. 670 Filters Library This section contains information on the following filters. Optical • Optical IIR filter • Measured Optical filter • Measured Group Delay Optical filter • Rectangle Optical filter • Trapezoidal Optical filter • Gaussian Optical filter • Butterworth Optical filter • Bessel Optical filter • Fabry Perot Optical filter • Acousto Optical filter • Mach-Zehnder Interferometer • Inverted Optical IIR filter • Inverted Rectangle Optical filter • Inverted Trapezoidal Optical filter • Inverted Gaussian Optical filter • Inverted Butterworth Optical filter • Inverted Bessel Optical filter • Gain Flattening Filter • Delay Interferometer • Transmission Filter Bidirectional • Reflective Filter Bidirectional • 3-Port Filter Bidirectional • Periodic Optical Filter 671 FILTERS LIBRARY FBG • Fiber Bragg Grating (FBG) • Uniform Fiber Bragg Grating • Ideal Dispersion Compensation FBG Electrical 672 • IIR filter • Low Pass Rectangle filter • Low Pass Gaussian filter • Low Pass Butterworth filter • Low Pass Bessel filter • Low Pass Chebyshev filter • Low Pass RC filter • Low Pass Raised Cosine filter • Low Pass Cosine Roll Off filter • Low Pass Squared Cosine Roll Off filter • Band Pass IIR filter (Obsolete) • Measured filter • Band Pass Rectangle filter • Band Pass Gaussian filter • Band Pass Butterworth filter • Band Pass Bessel filter • Band Pass Chebyshev filter • Band Pass RC filter • Band Pass Raised Cosine filter • Band Pass Cosine Roll Off filter • Band Pass Squared Cosine Roll Off filter • S Parameters Measured filter OPTICAL IIR FILTER Optical IIR filter Infinite impulse response filter (IIR) for optical signals. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 1000 GHz Hz, GHz, THz, nm [1e-9,+INF[ 0 dB — [0,+INF[ Z domain — — Frequency domain, Poles and zeros, Z domain Filter center frequency Filter sample rate User-defined sample rate independent from the signal sample rate Additional loss Loss applied to the signal after filtering Filter coefficients type Type of numerator and denominator coefficients for the filter Numerator coefficients Name and description Default value Units Value range Numerator coefficients 3 — [1,+INF[ Numerator[0].real 0.64 — ]-INF,+INF[ Numerator[0].imag 0 — ]-INF,+INF[ Number of numerator coefficients 673 OPTICAL IIR FILTER Name and description Default value Units Value range Numerator[1].real 1.28 — ]-INF,+INF[ Numerator[1].imag 0 — ]-INF,+INF[ Numerator[2].real 0.64 — ]-INF,+INF[ Numerator[2].imag 0 — ]-INF,+INF[ Name and description Default value Units Value range Denominator coefficients 3 — [1,+INF[ Denominator[0].real 5.05 — ]-INF,+INF[ Denominator[0].imag 0 — ]-INF,+INF[ Denominator[1].real –4.75 — ]-INF,+INF[ Denominator[1].imag 0 — ]-INF,+INF[ Denominator[2].real 2.26 — ]-INF,+INF[ Denominator[2].imag 0 — ]-INF,+INF[ Denominator coefficients Number of denominator coefficients Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ False — — True, False Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Digital filter Determines whether or not the individual samples filter is digital 674 OPTICAL IIR FILTER Noise Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The infinite impulse response filter is a recursive digital filter. The transfer function can be expressed in the z domain as: N α ∑ an z –n n=0 H ( z ) = ----------------------M ∑b m z –m m=0 where H(z) is the filter transfer function in the Z domain, α is the parameter for Additional loss, N is the parameter number of Numerator coefficients, an are the coefficients for the numerator, M is the parameter number of Denominator coefficients, and bm are the coefficients for the denominator. Also, z = exp ( j2π ( f – f c ) ⁄ f s ) where fc is the filter center frequency defined by the parameter Frequency, fs is the parameter Filter sample rate, and f is the frequency. According to the parameter Filter coefficients type, the filter transfer function can be given in the z (Z domain) or in the frequency domain. In the second case, the filter is determined by the numerator and the denominator polynomial, which can be expressed by their roots (Poles and zeros) or by the polynomial coefficients (in Frequency domain). Note: Individual samples require that the filter coefficients are given in the z domain. 675 OPTICAL IIR FILTER Notes: 676 MEASURED OPTICAL FILTER Measured Optical filter Filter based on measurements. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range User-defined frequency True — — True, False 193.1 THz Hz, THz, nm [0,+INF[ Name and description Default value Units Value range File frequency unit Hz — Hz, GHz, THz, m, nm Power — Power, Power Phase, Real Imag, phase True — ]-INF,+INF[ Determines whether you can define the filter center frequency or use the value from the measurements Frequency User-defined filter center frequency Measurements Determines the frequency unit of the file with the measurements File format Determines the format of the file with the measurements Linear scale Determines whether the measured data is in linear scale or not 677 MEASURED OPTICAL FILTER Name and description Default value Units Value range Filter filename Filter.dat — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Filename with the measured data Numerical Determines the interpolation algorithm for the measured data Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 678 MEASURED OPTICAL FILTER Graphs Name and description X Title Y Title Filter transmission - real part Frequency (Hz) Amplitude (a.u.) Filter transmission - imag part Frequency (Hz) Amplitude (a.u.) Technical background The input file is formatted containing two items per line — frequency and filter measurement. The parameter File frequency unit determines the frequency or wavelength unit of the first item. It can be in Hz, THz, m, or nm. According to the parameter File format, the second item can be one value (Power or Phase) or two values (Power and Phase or Real and Imag): Power (Phase is set to zero, assuming frequency unit is THz) 193.10 0 193.11 0.5 193.12 0.5 193.13 0 ... Power Phase 193.10 0 0 193.11 0.5 3.14 193.12 0.5 3.14 193.13 0 0 ... 679 MEASURED OPTICAL FILTER Real Imag 193.10 0 193.11 –0.5 7.9e-4 193.12 –0.5 7.9e-4 193.13 0 0 ... Phase (Power is set to one) 193.10 0 193.11 3.14 193.12 3.14 193.13 0 ... The parameter User defined frequency determines if you can enter the center frequency. This means that the filter data is shifted from the measured center frequency to the user center frequency that you define in the parameter Frequency. 680 MEASURED GROUP DELAY OPTICAL FILTER Measured Group Delay Optical filter Loads files with the filter amplitude and group delay ripple measurements. This FBG was designed mainly for dispersion compensation. Ports Name and description Port type Signal type Input Input Optical Transmission Output Optical Parameters Main Name and description Default value Default unit Units Value range User-defined frequency True — — True, False 193.1 THz Hz, THz, nm [0,+INF[ Name and description Default value Units Value range File frequency unit m — nm, m ps — s, pss Delay — Power, Power Delay, Delay Determines whether you can define the filter center frequency or use the value from the measurements Frequency User-defined filter center frequency Measurements Determines the frequency unit of the file with the measurements Group delay unit Determines the group delay unit of the file with the measurements File format Determines the format of the file with the measurements 681 MEASURED GROUP DELAY OPTICAL FILTER Name and description Default value Units Value range Linear scale True — True, False GroupDelay.dat — — False — True, False Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Determines whether or not the measured data is in linear scale Filename Filename with the measured data Reload file Defines whether the component should reload the filter data for each run Numerical Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz [1e-9,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 682 MEASURED GROUP DELAY OPTICAL FILTER Graphs Name and description X Title Y Title Filter transmission — Amplitude Wavelength (m) Amplitude (a.u.) Filter transmission — Phase Wavelength (m) Phase (rad) Technical background This model is a filter with measured group delay. The filter transfer function is H(f) = e jφ ( f ) (1) where f is the frequency dependence phase of the filter. The group delay is defined by Equation 1: 1- dφ τ ( f ) = – ---------2π df (2) Writing Equation 2 as a function of wavelength: 2 λ dφ τ ( λ ) = --------- -----2πc dλ (3) where c is the speed of light. You define τ by entering the table with the measurements. Typically, this measurement looks like the graph in Figure 1, where X is the wavelength in nm and Y is the group delay in ps: 683 MEASURED GROUP DELAY OPTICAL FILTER Figure 1 Group delay measurement Calculate the phase from this curve in order to calculate the filter transfer function. Phase calculation The phase is calculated with Equation 3: 1- dλ φ = 2πc ∫ τ ( λ ) ---2 λ (4) File format The input file is formatted with two items per line — the wavelength and the filter measurement. The parameter File frequency unit determines the wavelength unit of the first item, and can be in m or in nm. The parameter Group delay unit determines the group delay unit, and can be in s or in ps. According to the parameter File format, the second item can be one value (Power or Delay) or two values (Power and Delay). 684 MEASURED GROUP DELAY OPTICAL FILTER Example of input file: Power (Delay is set to zero) 1551 0 1551.1 0.5 1551.2 0.5 1551.3 0 ... Power Delay 1551 0 0 1551.1 0.5 –10 1551.2 0.5 –20 1551.3 0 –30 ... Delay (Power is set to one) 1551 0 1551.1 –10 1551.2 –20 1551.3 –30 ... The parameter User defined frequency determines if you can enter the center frequency. This means that the filter data is shifted from the measured center frequency to the user center frequency that you define in the parameter Frequency. 685 MEASURED GROUP DELAY OPTICAL FILTER References [1] Madsen, C. K. and Zhao, J H., Optical Filter Design and Analysis: A Signal Processing Approach. John Wiley & Sons, USA, (1999). 686 RECTANGLE OPTICAL FILTER Rectangle Optical filter Optical filter with a rectangle frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Default unit Units Value range Enabled True — — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 687 RECTANGLE OPTICAL FILTER Name and description Default value Default unit Units Value range Resample False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The filter transfer function is: ⎧ α, ⎫ H(f) = ⎨ ⎬ ⎩ d, ⎭ fc – B ⁄ 2 < f < fc + B ⁄ 2 otherwise where H(f) is the filter transfer function, α is the parameter Insertion loss, d is the parameter Depth, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and f is the frequency. 688 TRAPEZOIDAL OPTICAL FILTER Trapezoidal Optical filter Optical filter with a trapezoidal frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 100 GHz Hz, GHz, THz, nm ]0,+INF[ 3 dB — [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Filter center frequency Zero dB bandwidth Filter bandwidth at 0 dB Bandwidth Filter bandwidth at cutoff magnitude Cutoff magnitude Attenuation at the filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter 689 TRAPEZOIDAL OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The filter transfer function is:where 1–A ------------------------------- ( f – f2 ) ⎧ 10B – B 0dB ⎪ α.10 , ⎪ H(f) = ⎨ α, ⎪ 1–A - f -----------------------------( – f1) ⎪ 10B – B 0dB ⎩ α.10 , f > f2 f1 < fc < f2 f < f1 f 1 = f c – B 0dB ⁄ 2 f 2 = f c + B0dB ⁄ 2 and H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth at the cutoff magnitude, B0dB is the parameter Zero dB bandwidth, and f is the frequency. 690 GAUSSIAN OPTICAL FILTER Gaussian Optical filter Optical filter with a Gaussian frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 691 GAUSSIAN OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The filter transfer function is: 2N H ( f ) = αe ( f – fc ) ⎞ ⎛ 2-----------------------⎠ – 1n 2 ⎝ B where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, N is the parameter Order, and f is the frequency. 692 BUTTERWORTH OPTICAL FILTER Butterworth Optical filter Optical filter with a Butterworth frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 693 BUTTERWORTH OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background Butterworth filters are a class of all-pole filters with maximally flat frequency response. The filter transfer function is: N α(B ⁄ 2 ) H ( f ) = -----------------------------------------N–1 ∏ ( j ( f – fc ) – pk ) k=0 where pk = B --- ⋅ e 2 π 2k + 1 j --- ⎛⎝ 1 + ---------------⎞⎠ 2 N and H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, N is the parameter Order, and f is the frequency. 694 BESSEL OPTICAL FILTER Bessel Optical filter Optical filter with a Bessel frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 695 BESSEL OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 696 BESSEL OPTICAL FILTER Technical background Bessel filters have a transfer function of the form: d0 H ( s ) = α ------------BN ( s ) α is the parameter Insertion loss, N is the parameter Order, and ( 2N )!d 0 = --------------N 2 ⋅ N! is a normalizing constant and BN(s) is an nth-order Bessel polynomial of the form N BN ( s ) = ∑ dk s k k=0 where ( 2N – k )! d k = --------------------------------------N–k 2 ⋅ k! ( N – k )! and 2 ( f – f c ) ⋅ w b⎞ s = j ⎛ -----------------------------⎠ ⎝ B where fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and Wb denotes the normalized 3 dB bandwidth and can be approximated by w b ≈ ( 2N – 1 ) ⋅ ln 2 for N≥ 10 For N<10, a table of values for each Wb is used and the exact value of the bandwidth is obtained. 697 BESSEL OPTICAL FILTER Important: Previous versions older than OptiSystem 7.0 used a different equation to estimate the 3 dB bandwidth. The following table provides the multiplication factor that has to be multiplied by the current bandwidth in order to obtain the same results of versions older than OptiSystem 7.0: 698 Filter order Multiplication factor 1 1.1989 2 0.9476 3 0.9476 4 0.9581 5 0.9791 6 0.9791 7 0.9895 8 0.9895 9 0.9895 10 0.9895 FABRY PEROT OPTICAL FILTER Fabry Perot Optical filter Optical filter with a Fabry Perot frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 500 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Filter center frequency Bandwidth 3 dB filter bandwidth Free spectral range Free spectral range of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter 699 FABRY PEROT OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The filter transfer function is: 1–R H ( f ) = α ---------------------------------(f – f ) 1 – R∗ e c2πJ ---------------B where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and f is the frequency. where 2 2 πB-⎞ – ⎛ 2 + ---------πB-⎞ – 4 2 + ⎛⎝ ---------⎠ ⎝ FSR FSR⎠ R = ---------------------------------------------------------------------------2 where FSR is the parameter Free spectral range. 700 ACOUSTO OPTICAL FILTER Acousto Optical filter Optical filter with an Acousto optical frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Transmission Ouput Optical Reflection Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 100 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Default unit Units Value range Number of channels 4 — — [1,+INF[ 193.1 THz Hz, THz, nm [0,+INF[ 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Channels Number of filter channels Frequency[0] Filter center frequency 0 701 ACOUSTO OPTICAL FILTER Name and description Default value Default unit Units Value range Frequency[1] 193.2 THz Hz, THz, nm [0,+INF[ 193.3 THz Hz, THz, nm [0,+INF[ 193.4 THz Hz, THz, nm [0,+INF[ Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Filter center frequency 1 Frequency[2] Filter center frequency 2 Frequency[3] Filter center frequency 3 Simulation Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 702 ACOUSTO OPTICAL FILTER Technical background The filter transfer function is described using a sum of power transfer functions of the type sin ( k ( f – f c ) ⁄ B ) H n ( f ) = α --------------------------------------( k ( f – f nc ) ⁄ B ) where k=2.78311475, Hn(f) is the filter transfer function for each channel, α is the parameter Insertion loss, fnc is the filter center frequency defined by the parameter Frequency for each channel n, B is the parameter Bandwidth, and f is the frequency. 703 ACOUSTO OPTICAL FILTER Notes: 704 MACH-ZEHNDER INTERFEROMETER Mach-Zehnder Interferometer Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters MainSimulation Name and description Default value Default unit Units Value range Delay 0 s s, ms, ns [1e-9,+INF[ 0.5 — — [0,1] 0 dB — [0,+INF[ True — — True, False Name and description Default value Units Value range Discrete delay True — True, False Time delay of the first path Coupling coefficient Cross coupling coefficients Additional loss Loss applied to the signal at the output Conjugate Defines whether the component uses the complex conjugate definition or not If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value 705 MACH-ZEHNDER INTERFEROMETER Technical background The Mach-Zehnder filter is tunable and consists of two couplers, which are connected by two waveguides. The filter transfer function for such a case is defined by: H ( f ) = H coupler ( f )H τ H coupler ( f ) where H(f) is the filter transfer function and f is the frequency. with: H coupler ( f ) = 1 – α pj α 1–α pj α where α is the parameter Coupling coefficient. If the parameter Conjugate is disabled, p is positive (value = 1), and the coupler will use the definition of [1], otherwise p is negative (value = -1) and the coupler will use the definition of [2]. Hτ ( f ) = e – j2πfτ 0 0 1 where t is the parameter time Delay. References [1] Gerd Keiser, “Optical Fiber Communications,” Third Edition, McGraw-Hill, Higher Education, 2000. [2] Christi K. Madsen and Jian H. Zhao, "Optical Filter Design and Analysis, A Signal Processing Approach", (John Wiley & Sons, New York, 1999). 706 INVERTED OPTICAL IIR FILTER Inverted Optical IIR filter Inverted infinite impulse response filter (IIR) for optical signals. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm [1e-9,+INF[ 0 dB — [0,+INF[ Z domain — — Frequency domain, Poles and zeros, Z domain Filter center frequency Filter sample rate User-defined sample rate independent from the signal sample rate Additional loss Loss applied to the signal after filtering Filter coefficients type Type of numerator and denominator coefficients for the filter 707 INVERTED OPTICAL IIR FILTER Numerator coefficients Name and description Default value Units Value range Numerator coefficients 3 — [1,+INF[ Numerator[0].real 0.64 — ]-INF,+INF[ Numerator[0].imag 0 — ]-INF,+INF[ Numerator[1].real 1.28 — ]-INF,+INF[ Numerator[1].imag 0 — ]-INF,+INF[ Numerator[2].real 0.64 — ]-INF,+INF[ Numerator[2].imag 0 — ]-INF,+INF[ Name and description Default value Units Value range Denominator coefficients 3 — [1,+INF[ Denominator[0].real 5.05 — ]-INF,+INF[ Denominator[0].imag 0 — ]-INF,+INF[ Denominator[1].real –4.75 — ]-INF,+INF[ Denominator[1].imag 0 — ]-INF,+INF[ Denominator[2].real 2.26 — ]-INF,+INF[ Denominator[2].imag 0 — ]-INF,+INF[ Number of numerator coefficients Denominator coefficients Number of denominator coefficients Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate 708 INVERTED OPTICAL IIR FILTER Noise Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The transfer function is of the form: H ( f ) = α 1 – H IIR ( f ) 2 where H(f) is the filter transfer function, α is the parameter Insertion loss, HIIR(f) is the IIR filter transfer function (see Optical IIR filter), and f is the frequency. 709 INVERTED OPTICAL IIR FILTER Notes: 710 INVERTED RECTANGLE OPTICAL FILTER Inverted Rectangle Optical filter Optical filter with an inverted rectangle frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Default unit Units Value range Enabled True — — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 711 INVERTED RECTANGLE OPTICAL FILTER Name and description Default value Default unit Units Value range Resample False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The transfer function is of the form: H ( f ) = α 1 – H Rect ( f ) 2 where H(f) is the filter transfer function, α is the parameter Insertion loss, HRect(f) is the rectangle filter transfer function (see Rectangle Optical filter), and f is the frequency. 712 INVERTED TRAPEZOIDAL OPTICAL FILTER Inverted Trapezoidal Optical filter Optical filter with an inverted trapezoidal frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] Zero dB bandwidth 10 GHz Hz, GHz, THz, nm [1e-9,+INF[ Bandwidth 100 GHz Hz, GHz, THz, nm [1e-9,+INF[ Cutoff magnitude 3 dB — [0,+INF[ Insertion loss 0 dB — [0,+INF[ 100 dB — [0,+INF[ Filter center frequency 3 dB filter bandwidth Insertion loss of the filter Depth Maximum attenuation value for the filter 713 INVERTED TRAPEZOIDAL OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,0[ 3 dB [0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 714 INVERTED GAUSSIAN OPTICAL FILTER Inverted Gaussian Optical filter Optical filter with an inverted gaussian frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 715 INVERTED GAUSSIAN OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,0[ 3 dB [0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The transfer function is: H ( f ) = α 1 – H Gauss ( f ) 2 where H(f) is the filter transfer function, α is the parameter Insertion loss, HGauss(f) is the filter transfer function (see Gaussian Optical filter), and f is the frequency. 716 INVERTED BUTTERWORTH OPTICAL FILTER Inverted Butterworth Optical filter Optical filter with an inverted Butterworth frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 717 INVERTED BUTTERWORTH OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,0[ 3 dB [0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The transfer function is: H ( f ) = α 1 – HB ( f ) 2 where H(f) is the filter transfer function, α is the parameter Insertion loss, HB(f) is the filter transfer function (see Butterworth Optical filter), and f is the frequency. 718 INVERTED BESSEL OPTICAL FILTER Inverted Bessel Optical filter Optical filter with an inverted Bessel frequency transfer function. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1,100] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function 719 INVERTED BESSEL OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,0[ Noise dynamic 3 dB [0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Technical background The transfer function is: H ( f ) = α 1 – HB ( f ) 2 where H(f) is the filter transfer function, α is the parameter Insertion loss, HB(f) is the filter transfer function (see Bessel Optical filter), and f is the frequency. 720 GAIN FLATTENING FILTER Gain Flattening Filter This component is a filter the can be optimized for gain flattening filter or signal equalization applications. It can be used alone or combined with OptiSystem optimization engines. Ports Name and description Port type Signal type Input Input Optical Transmission Ouput Optical Reflection Output Optical Parameters Main Name and description Default value Units Value range Number of channels 4 — — Number of points for the frequency and transmission parameters Channels Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] Frequency for transmission value 0 Frequency[1] Frequency for transmission value 1 Frequency[2] Frequency for transmission value 2 721 GAIN FLATTENING FILTER Name and description Default value Default unit Units Value range Frequency[3] 193.4 THz Hz, THz, nm [30,3e5] 0 dB dB ]-INF,0] 0 dB dB ]-INF,0] 0 dB dB ]-INF,0] 0 dB dB ]-INF,0] Name and description Default value Units Value range Interpolation Cubic — Linear, Cubic Frequency for transmission value 3 Transmission[0] Transmission value for frequency 0 Transmission[1] Transmission value for frequency 1 Transmission[2] Transmission value for frequency 2 Transmission[3] Transmission value for frequency 3 Numerical Determines the interpolation algorithm for the measured data Graphs Name and description Default value Default unit Units Value range Calculate graphs False — — True, False 100 — — [10,100e6] 1500 nm nm [100,2000] 1600 nm nm [100,2000] Define whether to calculate graphs or not Number of points Number of points for the graphs From Wavelength lower limit for the graph To Wavelength upper limit for the graph 722 GAIN FLATTENING FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Name and description X Title Y Title Transmission Wavelength (m) Transmission (dB) Technical background This component allows for easy access to the filter transmission properties. Users can change the number of points by changing the parameter Number of channels. The values for the frequency and transmission points define the filter transfer function. For gain flattening applications for optical amplifiers, the values of the frequency points typically are the same as the values for the input signal channel center frequencies. OptiSystem optimization engines can estimate the values for the transmission in order to minimize the ration between minimum and maximum gain (ripple) between two points in the system. The second output port provides the inverse transfer function of the filter. This component can also generate the graph for the filter transmission using a user defined range and number of points. The graphs can be exported as a file, the user can select between linear or cubic interpolation. 723 GAIN FLATTENING FILTER Notes: 724 DELAY INTERFEROMETER Delay Interferometer The component simulates a delay interferometer with wavelength dependence. Ports Name and description Port type Signal type Input1 Input Optical Output1 Output Optical Output2 Output Optical Parameter Main Name and description Symbol Default unit Units Value range Delay Δt 25e-3 s, ms, ns [0, 1e100] ΔF 700 MHz [0, 1e100] α IL 30 dB [0, 100] α PDL 0.05 dB [0, 100] α EL 0.35 dB [0, 100] λR 1550 Hz, THz, nm [1300, 1800] Time delay applied in one of the interferometer arms PDF Polarization-dependent frequency shift IL Maximum insertion loss PDL Polarization-dependent loss Additional loss Excess loss Reference wavelength Wavelength that will be referenced for the time delay 725 DELAY INTERFEROMETER Technical Background The Delay Interferometer basically considers that difference between the two arms of a fiber optic interferometer is wavelength dependent and polarization sensitive. Fig. 1 shows a general schematic of the interferometer. where the phase delay difference between the arms, ΔΦ , is proportional to the signal wavelength and its simulation is implemented by applying the Jones matrix to the input signal. The Jones matrix is calculated based on the main parameters set by the user. 726 TRANSMISSION FILTER BIDIRECTIONAL Transmission Filter Bidirectional This component is bidirectional filter. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Units Filter type Rectangle [Rectangle, Gaussian, Butterworth, Bessel, Raised cosine, Trapezoidal] 2 [1, 100] 0.5 [0, 1] Defines the filter shape Order Value range Gaussian, Bessel or Butterworth filter order Roll off factor Raised cosine filter roll off factor Zero dB bandwidth 0.01 Hz, THz, nm [100, 2000] 1550 Hz, THz, nm [100, 2000] 0.1 Hz, GHz, THz, nm [0, 200] Defines the trapezoidal filter zero dB bandwidth Center wavelength Defines the filter center wavelength Bandwidth Defines the filter bandwidth 727 TRANSMISSION FILTER BIDIRECTIONAL Name and description Default value Units Value range Insertion loss 0 dB [0, +INF] 100 dB [0, +INF] 65 dB [0, +INF] Component insertion loss at the operating wavelength Max. insertion loss Component insertion loss outside the operating bandwidth Return loss Component return loss at the operating wavelength Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Current lower limit for the graphs To Current upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Defines whether to adapt the noise bins or not Noise threshold Minimum value for adaptation of noise bins 728 -100 dB [-INF, +INF] TRANSMISSION FILTER BIDIRECTIONAL Name and description Default value Noise dynamic Default unit Units Value range 3 dB [-INF +INF] Name and description X Title Y Title Transmission Wavelength (m) Transmission Threshold ratio for adaptation of noise bins Graphs Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 IL ( f )T ( f ) + E In 1 E Out 2 = E In1 IL ( f )T ( f ) + E In 2 (1) where T(f) is the filter transmission and RL is the return loss: T ( f ) = 10 RL = 10 – IL -------20 H( f) – RL ---------20 where IL is defined by the parameter Insertion loss and T(f) has the maximum value defined by the parameter Max. insertion loss. RL is defined by the parameter Return loss. The parameter Filter type defines the calculation equation for H(f). Filter H(f) from component Parameters Rectangle Rectangle Optical Filter Center wavelength, Bandwidth Gaussian Gaussian Optical Filter Center wavelength, Bandwidth, Order Butterworth Band Pass Butterworth Filter Center wavelength, Bandwidth, Order Raised cosine Raised Cosine Butterworth Filter Center wavelength, Bandwidth, Roll off factor Trapezoidal Trapezoidal Optical Filter Center wavelength, Bandwidth, Zero dB bandwidth If the parameter Calculate graphs is enabled, the component will generate graphs with the filter transmission. 729 TRANSMISSION FILTER BIDIRECTIONAL Notes: 730 REFLECTIVE FILTER BIDIRECTIONAL Reflective Filter Bidirectional This component is bidirectional reflective filter. It can be used as a fiber brag-grating filter. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Units Filter type Rectangle [Rectangle, Gaussian, Butterworth, Bessel, Raised cosine, Trapezoidal] 2 [1, 100] 0.5 [0, 1] Defines the filter shape Order Value range Gaussian, Bessel or Butterworth filter order Roll off factor Raised cosine filter roll off factor Zero dB bandwidth 0.01 Hz, THz, nm [100, 2000] 1550 Hz, THz, nm [100, 2000] Defines the trapezoidal filter zero dB bandwidth Center wavelength Defines the filter center wavelength 731 REFLECTIVE FILTER BIDIRECTIONAL Name and description Default value Units Value range Bandwidth 0.1 Hz, GHz, THz, nm [0, 200] 99 %, dB [0, 100] 0.01 %, dB [0, 100] 0 dB [0, +INF] Defines the filter bandwidth Reflection Component reflection at the operating wavelength Min. reflection Component reflection outside the operating bandwidth Insertion loss Component insertion loss at the operating wavelength Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Current lower limit for the graphs To Current upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Defines whether to adapt the noise bins or not 732 Default unit Units Value range [True, False] REFLECTIVE FILTER BIDIRECTIONAL Name and description Default value Noise threshold Default unit Units Value range -100 dB [-INF, +INF] 3 dB [-INF +INF] Name and description X Title Y Title Reflection Wavelength (m) Reflection Transmission Wavelength (m) Transmission Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 IL ⋅ T ( f ) + R ( f )E In 1 E Out 2 = E In1 IL ⋅ T ( f ) + R ( f )E In 2 (1) where T(f) and R(f) are frequency/wavelength transmission and reflection, respectively. IS is the insertion loss: T(f) = R 1 – H(f) R(f) = RH ( f ) IL = 10 2 – IL -------20 where IL is defined by the parameter Insertion loss. R is defined by the parameter Reflection and R(f) has the minimum value defined by the parameter Min. reflection. 733 REFLECTIVE FILTER BIDIRECTIONAL Notes: The parameter Filter type defines the calculation equation for H(f). Filter H(f) from component Parameters Rectangle Rectangle Optical Filter Center wavelength, Bandwidth Gaussian Gaussian Optical Filter Center wavelength, Bandwidth, Order Butterworth Band Pass Butterworth Filter Center wavelength, Bandwidth, Order Raised cosine Raised Cosine Butterworth Filter Center wavelength, Bandwidth, Roll off factor Trapezoidal Trapezoidal Optical Filter Center wavelength, Bandwidth, Zero dB bandwidth If the parameter Calculate graphs is enabled, the component will generate graphs with the filter transmission and reflection. 734 3-PORT FILTER BIDIRECTIONAL 3-Port Filter Bidirectional This component is 3-port bi-directional filter. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Parameters Main Name and description Default value Units Filter type Rectangle [Rectangle, Gaussian, Butterworth, Bessel, Raised cosine, Trapezoidal] 2 [1, 100] 0.5 [0, 1] Defines the filter shape Order Value range Gaussian, Bessel or Butterworth filter order Roll off factor Raised cosine filter roll off factor Zero dB bandwidth 0.01 Hz, THz, nm [100, 2000] 1550 Hz, THz, nm [100, 2000] Defines the trapezoidal filter zero dB bandwidth Center wavelength Defines the filter center wavelength 735 3-PORT FILTER BIDIRECTIONAL Name and description Default value Units Value range Bandwidth 0.1 Hz, GHz, THz, nm [0, 200] 0 dB [0, +INF] 0 dB [0, +INF] 100 dB [0, +INF] 100 dB [0, +INF] 65 dB [0, +INF] Defines the filter bandwidth Insertion loss 1->2 Component insertion loss from port 1 to 2 at the operating wavelength Insertion loss 1->3 Component insertion loss from port 1 to 3 at the operating wavelength Max. insertion loss 1->2 Component insertion loss outside the operating bandwidth from port 1 to 2 Max. insertion loss 1->3 Component insertion loss outside the operating bandwidth from port 1 to 3 Return loss Component return loss at the operating wavelength Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Current lower limit for the graphs To Current upper limit for the graphs Simulation Determines whether or not the component is enabled 736 [True, False] 3-PORT FILTER BIDIRECTIONAL Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF +INF] Name and description X Title Y Title Transmission 1->2 Wavelength (m) Transmission Transmission 1->3 Wavelength (m) Transmission Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 T 12 ( f ) + E In3 T 13 ( f ) + E In 1 RL E Out 2 = E In1 T 12 ( f ) + E In2 RL E Out 3 = E In1 T 13 ( f ) + E In3 RL where T(f) is the filter transmission and RL is the return loss: T 13 ( f ) = 10 T 12 ( f ) = 10 RL = 10 – IL 13 ------------20 – IL 12 -----------20 H(f) 1 – H(f) 2 – RL ---------20 737 3-PORT FILTER BIDIRECTIONAL where IL12 and IL12 are defined by the parameters Insertion loss 1->2 and 1->3. T12(f) and T13(f) have the maximum values defined by the parameters Max. insertion loss 1->2 and 1->3. RL is defined by the parameter Return loss. The parameter Filter type defines the calculation equation for H(f). Filter H(f) from component Parameters Rectangle Rectangle Optical Filter Center wavelength, Bandwidth Gaussian Gaussian Optical Filter Center wavelength, Bandwidth, Order Butterworth Band Pass Butterworth Filter Center wavelength, Bandwidth, Order Raised cosine Raised Cosine Butterworth Filter Center wavelength, Bandwidth, Roll off factor Trapezoidal Trapezoidal Optical Filter Center wavelength, Bandwidth, Zero dB bandwidth If the parameter Calculate graphs is enable the component will generate graphs with the filter transmission 1->2 and 1->3. 738 PERIODIC OPTICAL FILTER Periodic Optical Filter This component is a periodic optical filter with user defined shape and free spectral range. Ports Name and description Port type Signal type Input 1 Input Optical Output 1 Output Optical Parameters Main Name and description Default value Units Value range Frequency 193.1 Hz, THz, nm [30, 300000] 10 Hz, GHz, THz, nm [0, 1e100] 800 Hz, GHz, THz, nm [0, 1e100] 0 dB [0, 1e100] 100 dB [0, 1e100] Filter center frequency Bandwidth 3 dB filter bandwidth Free spectral range Free spectral range of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Filter type Gaussian Rectangle, Gaussian, Bessel 2 [1, 100] Defines the filter shape Filter order Gaussian or Bessel filter order 739 PERIODIC OPTICAL FILTER Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz [1e-9,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Name and description Default value Noise threshold Default unit Units Value range -100 dB [-INF, +INF] 3 dB [-INF +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 740 PERIODIC OPTICAL FILTER Technical Background The central frequency of the internal filter is calculated according to: ( f – fc ) n = --------------FSR (1) (2) f n = f c + n × FSR Where f is the signal frequency, f c is the parameter Frequency and FSR is the free spectral range. n calculated from (1) is an integer value. Using n the component estimates the value of the internal filter according to (2). The internal filter transmission is: T ( f ) = 10 – IL -------20 H( f) IL is the parameter insertion loss. The parameter Filter type defines the calculation equation for H(f). Filter H(f) from component Parameters Rectangle Rectangle Optical filter Frequency, Bandwidth Gaussian Gaussian Optical filter Frequency, Bandwidth, Order Bessel Bessel Optical filter Frequency, Bandwidth, Order 741 PERIODIC OPTICAL FILTER Notes: 742 FIBER BRAGG GRATING (FBG) Fiber Bragg Grating (FBG) Simulates an FBG. Ports Name and description Port type Signal type Input Input Optical Transmission Output Optical Reflection Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] 1.45 — — [1,10] 2 nm — [1e-6,1e3] Optical frequency of the center of the Fiber Bragg Grating reflection spectrum Effective index Modal index of the optical fiber grating Length Length of the optical fiber grating Apodization Name and description Default value Units Value range Apodization function Uniform — Uniform, Gaussian, Tanh, user-defined 0.5 — [0.01,100] Modulates the grating intensity over the grating length. Gauss parameter Apodization is defined by a Gaussian function using the S parameter. See Technical Background for the definition. 743 FIBER BRAGG GRATING (FBG) Name and description Default value Units Value range Tanh parameter 0.5 — [0.01,100] Apodization.dat — — 0.00001 — ]0,1e3] 0 — ]0,1e3] Name and description Default value Units Value range Chirp function None — None, Linear, Quadratic, Square root, Cubic root, userdefined 0.00001 μm [0.01,100] 0.00001 μm [0.01,100] 0.00001 μm [0.01,100] 0.00001 μm [0.01,100] ChirpPeriod.dat — — Apodization is defined by an hyperbolic tangent function using the S parameter. See Technical Background for the definition. Apodization filename You supply a file for the apodization. The ith element of this file is applied as the local apodization for the ith segment of the grating. Modulation AC Index modulation when the apodization is unity. The product of this number with the apodization function determines the local index modulation. Modulation DC Modifies the modal index of the fiber in proportion to the apodization function. Chirp Period that the grating can be changed over the length of the fiber. Linear parameter Period varies in a linear way, as defined in the Technical Background. Quadratic parameter Period varies in a quadratic way, as defined in the Technical Background. Square root parameter Period varies as defined in the Technical Background. Cubic root parameter Period varies as defined in the Technical Background. Chirp filename In the user-defined file, the ith entry is used as the period for the ith segment of the chirped grating. 744 FIBER BRAGG GRATING (FBG) Calculation Name and description Default value Units Value range Number of segments 101 — [1,1e9] 1000 — [100,1e6] The non-uniform grating will be divided into this number of equal length uniform segments to calculate the spectrum Max. number of spectral points Maximum nuber of points for the transmission and reflection complex spectrum Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz [1e-9,+INF[ Name and description Default value Default unit Units Value range Noise threshold –100 dB — ]-INF,0[ 3 dB — [0,+INF[ 1 THz Hz, GHz, THz, nm [0, 1e+100] Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Noise calculation bandwidth Calculation bandwidth — outside of this range, calculation is replaced by the attenuation 745 FIBER BRAGG GRATING (FBG) Technical background The non-uniform (chirped and apodized) grating [1] is divided into Number of Segments uniform gratings. The coupled mode theory is used to calculate the scattering matrix of each uniform segment, and the spectral response of the whole grating is found by connecting the uniform segments using the transfer matrix theory. The apodization functions Gaussian and Hyperbolic tangent are defined with the following parameters: Gaussian ⎧ ⋅ ( z – L ⁄ 2 )- 2 ⎫ A ( z ) = exp ⎨ – ln 2 ⋅ 2-----------------------------⎬ s⋅L ⎩ ⎭ Hyperbolic tangent 2 A ( z ) = tanh ( s ⋅ z ⁄ L ) ⋅ tanh [ s ⋅ ( 1 – z ⁄ L ) ] + 1 – tan h ( s ⁄ 2 ) When the parameter Apodization function is user-defined, you provide a file with the data describing the apodization. The input file is formatted containing two items per line — the length in μm and the apodization value. 0 7.99437714249507e-007 0.2 2.39785072153609e-006 0.4 3.99496320824255e-006 0.6 5.58995679966756e-006 0.8 7.18201727067935e-006 1.0 8.770334716246e-006 1.2 1.03541096905246e-005 . . . 746 FIBER BRAGG GRATING (FBG) The chirp functions depend on a parameter, Δ, which is used as follows: Linear z–L⁄2 Λ ( z ) = Λ 0 – ------------------Δ L Δ « Λ0 2 Λ ( z ) = Λ 0 – ⎛⎝ --z-⎞⎠ + 1--- Δ L 4 Δ « Λ0 Quadratic Square Root Λ( z ) = Λ0 – 1- Δ --z- – -----L 2 Δ « Λ0 1- Δ --z- – -----L 3 2 Δ « Λ0 Cubic Root Λ ( z ) = Λ0 – 3 747 FIBER BRAGG GRATING (FBG) When the parameter Chirp function is user-defined, you provide a file with the data describing the chirp. The input file is formatted containing two items per line — the length in μm and the chirp value in μm. 0 0.53368353843689 0.2 0.53369003534317 0.4 0.533694565296173 0.6 0.533698260784149 0.8 0.533701419830322 1.0 0.533704221248627 1.2 0.533706843852997 . . . References [1] Erdogan, R., “Fiber Grating Spectra”, J. Light. Technol., 15, 1277-1294, (1997). 748 UNIFORM FIBER BRAGG GRATING Uniform Fiber Bragg Grating Simulates a Uniform FBG. Ports Name and description Port type Signal type Input Input Optical Transmission Output Optical Reflection Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30,3e5] 125 GHz Hz, GHz, THz, nm [0,+INF[ 0.99 — — [1e-100, 1] Name and description Default value Default unit Units Value range Enabled True — — True, False Optical frequency of the center of the Fiber Bragg Grating reflection spectrum Bandwidth Width of the reflection stop band of the Fiber Bragg Grating Reflectivity Desired maximum reflectivity of the grating (maximum is at the centre wavelength) Simulation Determines whether or not the component is enabled 749 UNIFORM FIBER BRAGG GRATING Name and description Default value Default unit Units Value range Resample False — — True, False 500 GHz Hz, GHz, THz [1e-9,+INF[ Name and description Default value Default unit Units Value range Noise threshold –100 dB — ]-INF,0[ 3 dB — [0,+INF[ 1 THz Hz, GHz, THz, nm [0, 1e+100] Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Noise calculation bandwidth Calculation bandwidth, outside of this range calculation is replaced by the attenuation Technical background The solution to the coupled mode equations for a uniform grating is used. The unknown parameters in the grating (grating period, grating modulation intensity) are found by employing the information about maximum reflectivity and bandwidth. The result is a module for the calculation of the reflection and transmission spectra [1]. References [1] Agrawal, G.P., Fiber-Optic Communication Systems. John Wiley & Sons, New York, (1997). 750 IDEAL DISPERSION COMPENSATION FBG Ideal Dispersion Compensation FBG Approximation of an ideal chirped FBG designed for dispersion compensation. Ports Name and description Port type Signal type Input Input Optical Transmission Output Optical Reflection Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [0,+INF[ 10 GHz Hz, GHz, THz, nm ]0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 800 ps/nm ps/nm s/m ] -INF, +INF[ Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Dispersion Group delay slope 751 IDEAL DISPERSION COMPENSATION FBG Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 500 GHz Hz, GHz, THz [1e-9,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background This model is a filter with user-defined group delay. The filter transfer function is: H(f) = e jφ ( f ) (1) where f is the frequency dependence phase of the filter. The group delay is defined by [1]: 1 dφ τ ( f ) = – ------ -----2π df (2) Writing Equation 2 as a function of wavelength: 2 dφλ - ----τ ( λ ) = – -------2πc dλ where c is the speed of light. 752 (3) IDEAL DISPERSION COMPENSATION FBG You define τ by entering the center wavelength delay slope D in s/m: ⎧ τ0 ⎪ τ ( λ ) = ⎨ D.λ ⎪ ⎩ τλc + Δλ ⁄ 2 λ c , bandwidth Δ λ , and the group λ ≤ λc – Δλ ⁄ 2 λc – Δλ ⁄ 2 < λ ≤ λ c + Δλ ⁄ 2 λ > λc + Δλ ⁄ 2 This generates the following group delay curve: Figure 1 Group delay Calculate the phase from this curve to calculate the filter transfer function. Phase calculation The phase is calculated from Equation 3 and Equation 4: 1- dλ φ = – 2πc ∫ τ ( λ ) ---2 λ (4) 753 IDEAL DISPERSION COMPENSATION FBG λ ≤ λc – Δλ ⁄ 2 : λ 1- dλ = 2πcτ ⎛ --1- – ---1-⎞ φ = – 2πcτ 0 ∫ ---0⎝ ⎠ 2 λ λ 1 λ λ 1 λ 1 = – ∞, τ 0 = 0 φ = 0 (5) λc – Δλ ⁄ 2 < λ ≤ λc + Δλ ⁄ 2 : λ ( λ – λ1 ) λ φ = 2πcD ∫ ------------------dλ + φ λc – Δ λ ⁄ 2 = 2πcD ln ( λ ) – 2πcD ----1- + φ λc – Δ λ ⁄ 2 2 λ λ λ 1 φ λc – Δλ ⁄ 2 = 2πcD ln ( λ 1 ) – 2πcD ,λ 1 = ( λ c – Δ λ ⁄ 2 ) ( λc – Δλ ⁄ 2 ) - + 2πcD ln ( λ c – Δ λ ⁄ 2 ) – 2πcD φ = 2πcD ln ( λ ) – 2πcD ---------------------------λ (6) λ > λc + Δλ ⁄ 2 : λ 1- dλ + φ ⎛1 1 ⎞ φ = – 2πcτ λc – Δλ ⁄ 2 ∫ ---λ c – Δ λ ⁄ 2 = 2πcτ λ c – Δ λ ⁄ 2 ⎝ --- – -----⎠ + φ λ c – Δ λ ⁄ 2 2 λ λ1 λ λ 1 λ 1 = ( λ c + Δ λ ⁄ 2 ) ,λ 2 = λ ,τ λc – Δλ ⁄ 2 = – D ( Δ λ ) ( λc – Δλ ⁄ 2 ) φ λc – Δ λ ⁄ 2 = 2πcD ln ( λ c + Δ λ ⁄ 2 ) – 2πcD ----------------------------- + 2πcD ln ( λ c – Δ λ ⁄ 2 ) – 2πcD ( λc + Δλ ⁄ 2 ) 1 1 φ = – 2πcDΔ λ = ⎛ --- – ------------------------------⎞ + ⎝ λ ( λ + Δ ⁄ 2 )⎠ c λ ( λc – Δλ ⁄ 2 ) ⎛ 2πcD ln ( λ + Δ ⁄ 2 ) – 2πcD ----------------------------- + 2πcD ln ( λ c – Δ λ ⁄ 2 ) – 2πcD⎞⎠ c λ ⎝ (λ + Δ ⁄ 2) c λ (7) 754 IDEAL DISPERSION COMPENSATION FBG This generates the following typical phase curve (for Figure 2 D = – 0.8s ⁄ m : Cumulative phase References [1] Madsen, C. K. and Zhao, J H., Optical Filter Design and Analysis: A Signal Processing Approach. John Wiley & Sons, New York, (1999). 755 IDEAL DISPERSION COMPENSATION FBG Notes: 756 IIR FILTER IIR filter Infinite impulse response filter (IIR) for electrical signals. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Filter sample rate 10 GHz Hz, GHz [1e-9,+INF[ 0 dB dB [0,+INF[ Z domain — — Frequency domain, Poles and zeros, Z domain Name and description Default value Units Value range Numerator coefficients 3 — [1,+INF[ Numerator[0].real 0.64 — ]-INF,+INF[ Numerator[0].imag 0 — ]-INF,+INF[ Numerator[1].real 1.28 — ]-INF,+INF[ User-defined sample rate independent from the signal sample rate Additional loss Loss applied to the signal after filtering Filter coefficients type Type of numerator and denominator coefficients for the filter Numerator coefficients Number of numerator coefficients 757 IIR FILTER Name and description Default value Units Value range Numerator[1].imag 0 — ]-INF,+INF[ Numerator[2].real 0.64 — ]-INF,+INF[ Numerator[2].imag 0 — ]-INF,+INF[ Name and description Default value Units Value range Denominator coefficients 3 — [1,+INF[ Denominator[0].real 5.05 — ]-INF,+INF[ Denominator[0].imag 0 — ]-INF,+INF[ Denominator[1].real –4.75 — ]-INF,+INF[ Denominator[1].imag 0 — ]-INF,+INF[ Denominator[2].real 2.26 — ]-INF,+INF[ Denominator[2].imag 0 — ]-INF,+INF[ Name and description Default value Units Value range Enabled True — True, False False — True, False Denominator coefficients Number of denominator coefficients Simulation Determines whether or not the component is enabled Digital filter Determines whether or not the individual samples filter is digital 758 IIR FILTER Technical background The infinite impulse response filter is a recursive digital filter. The transfer function can be expressed in the z domain as: N ∑a z –n n n=0 H ( z ) = α ---------------------M ∑b m z –m m=0 where H(z) is the filter transfer function in the Z domain, α is the parameter related to Additional loss, N is the parameter number of Numerator coefficients, an are the coefficients for the numerator, M is the parameter number of Denominator coefficients, and bm are the coefficients for the denominator. Also z = exp ( j2πf ⁄ f s ) where fs is the parameter Filter sample rate, and f is the frequency. According to the parameter Filter coefficients type, the filter transfer function can be given in the z (z domain) or in the frequency domain. In the second case, the filter is determined by the numerator and the denominator polynomial, which can be expressed by their roots (Poles and zeros) or by the polynomial coefficients (in Frequency domain). Note: Individual samples require that the filter coefficients are given in the z domain. 759 IIR FILTER Notes: 760 LOW PASS RECTANGLE FILTER Low Pass Rectangle filter Optical filter with a rectangle frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 761 LOW PASS RECTANGLE FILTER Technical background The filter transfer function is: ⎧ α, H(f) = ⎨ ⎩ d, 0 < f < fc otherwise where H(f) is the filter transfer function,α is the parameter Insertion loss, d is the parameter Depth, fc is the cutoff frequency, and f is the frequency. 762 LOW PASS GAUSSIAN FILTER Low Pass Gaussian filter Optical filter with a Gaussian frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled 763 LOW PASS GAUSSIAN FILTER Technical background The filter transfer function is: H ( f ) = αe ⎛ f 2N⎞ – ln 2 ⎜ --------⎟ ⎝ fc ⎠ where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter cutoff frequency, N is the parameter Order, and f is the frequency. 764 LOW PASS BUTTERWORTH FILTER Low Pass Butterworth filter Optical filter with a Butterworth frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled 765 LOW PASS BUTTERWORTH FILTER Technical background Butterworth filters are a class of all-pole filters with maximally flat frequency response. In this case. the filter transfer function is: N ( fc ) H ( f ) = α -------------------------------N–1 ∏ ( j ( f ) – pk ) k=0 where pk = fc ⋅ e π 2k + 1 j -- ⎛⎝ 1 + --------------⎞⎠ 2 N where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter cutoff frequency, N is the parameter Order, and f is the frequency. 766 LOW PASS BESSEL FILTER Low Pass Bessel filter Filter with a Bessel frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 4 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False False — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled Digital filter Determines whether or not the individual samples filter is digital 767 LOW PASS BESSEL FILTER Technical background Bessel filters have the following transfer function: d0 H ( s ) = α -----------BN ( s ) where α is the parameter Insertion loss, N is the parameter Order, and ( 2N )!d 0 = --------------N 2 ⋅ N! being a normalizing constant and BN(s) an nth-order Bessel polynomial of the form: N BN ( s ) = ∑ dk s k k=0 where ( 2N – k )! d k = ----------------------------------------N–k 2 ⋅ k! ( N – k )! and f⋅w s = j ⎛⎝ -----------b-⎞⎠ f c where fc is the filter cutoff frequency defined by the parameter Frequency and Wb denotes the normalized 3 dB bandwidth and can be approximated by: w b ≈ ( 2N – 1 ) ⋅ ln 2 for N≥ 10 768 LOW PASS BESSEL FILTER For N<10, a table of values for each Wb is used and the exact value of the bandwidth is obtained. Important: Previous versions older than OptiSystem 7.0 used a different equation to estimate the 3 dB bandwidth. The following table provides the multiplication factor that has to be multiplied by the current bandwidth in order to obtain the same results of versions older than OptiSystem 7.0: Filter order Multiplication factor 1 1.1989 2 0.9476 3 0.9476 4 0.9581 5 0.9791 6 0.9791 7 0.9895 8 0.9895 9 0.9895 10 0.9895 769 LOW PASS BESSEL FILTER Notes: 770 LOW PASS CHEBYSHEV FILTER Low Pass Chebyshev filter Filter with a Chebyshev frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Ripple factor Ripple parameters Simulation Determines whether or not the component is enabled 771 LOW PASS CHEBYSHEV FILTER Technical background Chebychev of order N filters have the following transfer function: N–1 ∏ sk k=0 H ( s ) = – α ⋅ ------------------------N–1 ∏ ( s – sk ) k=0 where α is the parameter Insertion loss and N is the parameter Order. Also s = jf and s k = f c ⋅ ( sinh δ ⋅ cos β k + j ⋅ cosh δ ⋅ sin β k ) where fc is the filter cutoff frequency. The parameters: 1- ar sinh ( r –1 ) δ = --N and π(2(k + 1) + N – 1) β k = -----------------------------------------------2N where r = 1 –1 ------------1 – rp where rp is the parameter ripple factor. 772 LOW PASS RC FILTER Low Pass RC filter Filter with an RC frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 773 LOW PASS RC FILTER Technical background RC filter has the following transfer function: 1 H ( f ) = α ⋅ -------------1 + j ---f fc where α is the parameter Insertion loss and fc is the filter cutoff frequency. 774 LOW PASS RAISED COSINE FILTER Low Pass Raised Cosine filter Filter with a raised cosine frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll-off factor Simulation Determines whether or not the component is enabled 775 LOW PASS RAISED COSINE FILTER Technical background Raised cosine filter has the following transfer function: ⎧ α ⎪ ( 1 – rp ) ⎪ 2 π H ( f ) = ⎨ α ⋅ cos -------------Δf - ( f ) – ----------------2r 2 Δf ⎪ p ⎪ 0 ⎩ ( 1 – rp ) f < -----------------Δf 2 ( 1 – rp ) ( 1 + rp ) ------------------Δf ≤ f < ------------------ Δf 2 2 ( 1 + rp ) ------------------- Δf ≤ f 2 where 1 Δf = 2f c ⋅ -------------------------------------------------------------------1 – r p + 4 ⁄ π ⋅ r p ⋅ arc cos 4 2 where α is the parameter Insertion loss, fc is the filter cutoff frequency, and rp is the parameter Roll off factor. 776 LOW PASS COSINE ROLL OFF FILTER Low Pass Cosine Roll Off filter Filter with a cosine roll off frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll off factor Simulation Determines whether or not the component is enabled 777 LOW PASS COSINE ROLL OFF FILTER Technical background Cosine Roll Off Filter has the following transfer function:= ⎧ α ⎪ ⎪ f – f1 H ( f ) = ⎨ 0.5 ⋅ α 2 ⋅ 1 + cos ⎛ ------------------------ ⋅ π⎞⎠ ⎝ r p ⋅ Δf FWHM ⎪ ⎪ 0 ⎩ f < f1 f1 ≤ f < f 2 f2 ≤ f where a is the parameter Insertion loss, fc is the filter cutoff frequency, and rp is the parameter Roll off factor. The parameters f1 and f2 are: f 1 = ( 1 – r p )f c 0 ≤ rp ≤ 1 and f 2 = ( 1 + r p )f c 778 0 ≤ rp ≤ 1 LOW PASS SQUARED COSINE ROLL OFF FILTER Low Pass Squared Cosine Roll Off filter Filter with a square cosine roll off frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Cutoff frequency 0.75 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False 3 dB cutoff frequency of the filter Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll-off factor Simulation Determines whether or not the component is enabled 779 LOW PASS SQUARED COSINE ROLL OFF FILTER Technical background Square cosine roll off filter has the following transfer function: ⎧ α ⎪ ⎪ f –f H ( f ) = ⎨ 0.5 ⋅ α ⋅ 1 + cos ⎛ --------------1- ⋅ π⎞ ⎝ r p ⋅ Δf ⎠ ⎪ ⎪ 0 ⎩ f < f1 f1 ≤ f < f 2 f2 ≤ f where α is the parameter Insertion loss and rp is the roll off factor. The parameter Δ f is related to the filter frequency cutoff by: 2f c Δf = ------------------------------------------------------------------------------2 1 + --- ⋅ arc cos ( 2 – 1 ) – 1 ⋅ r p π where fc is the filter cutoff frequency. 780 BAND PASS IIR FILTER (OBSOLETE) Band Pass IIR filter (Obsolete) Infinite impulse response filter (IIR) for electrical signals. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 10 GHz Hz, GHz [1e-9,+INF[ 0 dB — [0,+INF[ Z domain — — Frequency domain, Poles and zeros, Z domain Filter center frequency Filter sample rate User-defined sample rate independent from the signal sample rate Additional loss Loss applied to the signal after filtering Filter coefficients type Type of numerator and denominator coefficients for the filter 781 BAND PASS IIR FILTER (OBSOLETE) Numerator coefficients Name and description Default value Units Value range Numerator coefficients 3 — [1,+INF[ Numerator[0].real 0.64 — ]-INF,+INF[ Numerator[0].imag 0 — ]-INF,+INF[ Numerator[1].real 1.28 — ]-INF,+INF[ Numerator[1].imag 0 — ]-INF,+INF[ Numerator[2].real 0.64 — ]-INF,+INF[ Numerator[2].imag 0 — ]-INF,+INF[ Name and description Default value Units Value range Denominator coefficients 3 — [1,+INF[ Denominator[0].real 5.05 — ]-INF,+INF[ Denominator[0].imag 0 — ]-INF,+INF[ Denominator[1].real –4.75 — ]-INF,+INF[ Denominator[1].imag 0 — ]-INF,+INF[ Denominator[2].real 2.26 — ]-INF,+INF[ Denominator[2].imag3 0 — ]-INF,+INF[ Name and description Default value Units Value range Enabled True — True, False Number of numerator coefficients Denominator coefficients Number of denominator coefficients Simulation Determines whether or not the component is enabled 782 BAND PASS IIR FILTER (OBSOLETE) Technical background The infinite impulse response filter is a recursive digital filter. The transfer function can be expressed in the z domain as: N ∑ an z –n n=0 H ( z ) = α ----------------------M ∑ bm z –m m=0 where H(z) is the filter transfer function in the Z domain, α is the parameter related to Additional loss, N is the parameter number of Numerator coefficients, an are the coefficients for the numerator, M is the parameter number of Denominator coefficients, and bm are the coefficients for the denominator. Also z = exp ( j2π ( f – f c ) ⁄ f s ) where fc is the filter center frequency defined by the parameter Frequency, fs is the parameter Filter sample rate, and f is the frequency. According to the parameter Filter coefficients type, the filter transfer function can be given in the z (Z domain) or in the frequency domain. In the second case, the filter is determined by the numerator and the denominator polynomial, which can be expressed by their roots (Poles and zeros) or by the polynomial coefficients (Frequency domain). 783 BAND PASS IIR FILTER (OBSOLETE) Notes: 784 MEASURED FILTER Measured filter Filter based on measurements. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range User-defined frequency True — — True, False 0 GHz Hz, MHz, GHz [0,+INF[ Name and description Default value Units Value range File frequency unit Hz — Hz, THz Power — Power, Power Phase, Real Imag, phase True — ]-INF,+INF[ Determines whether you can define the filter center frequency or use the value from the measurements Frequency User-defined filter center frequency Measurements Determines the frequency unit of the file with the measurements File format Determines the format of the file with the measurements Linear scale Determines whether or not the measured data is in linear scale 785 MEASURED FILTER Name and description Default value Units Value range Filename Filter.dat — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Name and description Default value Units Value range Enabled True — True, False Filename with the measured data Numerical Determines the interpolation algorithm for the measured data Simulation Determines whether or not the component is enabled Technical background The input file is formatted containing two items per line, the frequency and filter measurement. The parameter File frequency unit determines the frequency or wavelength unit of the first item; It can be in Hz or THz. According to the parameter File format the second item can be one value (Power or Phase) or two values (Power and Phase or Real and Imag): 786 MEASURED FILTER Power (Phase is set to zero, assuming frequency unit is THz) 193.10 0 193.11 0.5 193.12 0.5 193.13 0 ... Power Phase 193.10 0 0 193.11 0.5 3.14 193.12 0.5 3.14 193.13 0 0 ... Real Imag 193.10 0 193.11 –0.5 7.9e-4 193.12 –0.5 7.9e-4 193.13 0 0 ... 787 MEASURED FILTER Phase (Power is set to one) 193.10 0 193.11 3.14 193.12 3.14 193.13 0 ... The parameter User defined frequency determines if you can enter the center frequency. From the measured data, F c = ( Max + Min ) ⁄ 2 where F c is the center frequency of the loaded file, Max is the maximum frequency of the file, and Min is the minimum frequency of the file. If the option 'User Defined Frequency' is selected, then the center frequency of the loaded file becomes centered at the user defined frequency. 788 BAND PASS RECTANGLE FILTER Band Pass Rectangle filter Optical filter with a rectangle frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 789 BAND PASS RECTANGLE FILTER Technical background The filter transfer function is: f c – B ⁄ 2 < f < fc + B ⁄ 2 otherwise ⎧ α, H( f) = ⎨ ⎩ d, where H(f) is the filter transfer function, α is the parameter Insertion loss, d is the parameter Depth, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and f is the frequency. 790 BAND PASS GAUSSIAN FILTER Band Pass Gaussian filter Optical filter with a Gaussian frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled 791 BAND PASS GAUSSIAN FILTER Technical background The filter transfer function is: H ( f ) = αe ⎛ ( f – f )2N⎞ c – ln 2 ⎜ 2 ----------------------⎟ ⎜ ⎟ B ⎝ ⎠ where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, N is the parameter Order, and f is the frequency. 792 BAND PASS BUTTERWORTH FILTER Band Pass Butterworth filter Optical filter with a Butterworth frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled 793 BAND PASS BUTTERWORTH FILTER Technical background Butterworth filters are a class of all-pole filters with maximally flat frequency response. The filter transfer function is: N (B ⁄ 2) H ( f ) = α -----------------------------------------N–1 ∏ ( j ( f – fc ) – pk ) k=0 where pk = B --- ⋅ e 2 + 1-⎞ jπ --- ⎛ 1 + 2k -------------2⎝ N ⎠ where H(f) is the filter transfer function, α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, N is the parameter Order, and f is the frequency. 794 BAND PASS BESSEL FILTER Band Pass Bessel filter Filter with a Bessel frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 4 — — [1, 100] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Simulation Determines whether or not the component is enabled 795 BAND PASS BESSEL FILTER Technical background Bessel filters have the following transfer function: d0 H ( s ) = α -----------BN ( s ) where α is the parameter Insertion loss, N is the parameter Order, and ( 2N )!d 0 = --------------N 2 ⋅ N! is a normalizing constant and BN(s) is an nth-order Bessel polynomial of the form N BN ( s ) = ∑ dk s k k=0 where ( 2N – k )! d k = --------------------------------------N–k 2 ⋅ k! ( N – k )! and ( f – f c ) ⋅ w b⎞ s = j ⎛⎝ 2 --------------------------⎠ B where fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and Wb denotes the normalized 3 dB bandwidth and can be approximated by: w b ≈ ( 2N – 1 ) ⋅ ln 2 for N≥ 10 For N<10, a table of values for each Wb is used and the exact value of the bandwidth is obtained. 796 BAND PASS BESSEL FILTER Important: Previous versions older than OptiSystem 7.0 used a different equation to estimate the 3 dB bandwidth. The following table provides the multiplication factor that has to be multiplied by the current bandwidth in order to obtain the same results of versions older than OptiSystem 7.0: Filter order Multiplication factor 1 1.1989 2 0.9476 3 0.9476 4 0.9581 5 0.9791 6 0.9791 7 0.9895 8 0.9895 9 0.9895 10 0.9895 797 BAND PASS BESSEL FILTER Notes: 798 BAND PASS CHEBYSHEV FILTER Band Pass Chebyshev filter Filter with a Chebyshev frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 1 — — [1, 100] 0.01 — — [0, 1] Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Order Order of the function Ripple factor Bandpass ripple parameter 799 BAND PASS CHEBYSHEV FILTER Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Technical background Chebychev of order N filters have the following transfer function: N–1 ∏ sk k=0 N–1 H ( s ) = α ⋅ -------------------------- ∏ ( s – sk ) k=0 where α is the parameter Insertion loss and N is the parameter Order. with s = j ( f – fc ) where fc is the filter center frequency defined by the parameter Frequency. Here, Sk are the poles of the filter defined by: sk = B --- ⋅ ( sinh δ ⋅ cos β k + j ⋅ cosh δ ⋅ sin β k ) 2 where B is the parameter Bandwidth. and r = 1 –1 ------------1 – rp where rp is the parameter ripple factor. 1- ar sinh ( r –1 ) δ = --N and 800 ( 2 ( k + 1 ) + N – 1 -) βk = π ----------------------------------------------2N BAND PASS RC FILTER Band Pass RC filter Filter with an RC frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Simulation Determines whether or not the component is enabled 801 BAND PASS RC FILTER Technical background RC filter has the following transfer function: 1 H ( f ) = α ⋅ ------------------------f – fc 1 + j2 ----------B where α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, and B is the parameter Bandwidth. 802 BAND PASS RAISED COSINE FILTER Band Pass Raised Cosine filter Filter with a raised cosine frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll off factor Simulation Determines whether or not the component is enabled 803 BAND PASS RAISED COSINE FILTER Technical background Raised cosine filter has the following transfer function: ⎧ α ⎪ ⎪ 2 π ( – ) ( 1 – rp ) H ( f ) = ⎨ α ⋅ cos ------------- f f c – ------------------Δf 2r p Δf 2 ⎪ ⎪ 0 ⎩ ( 1 – rp ) f – f c < -----------------Δf 2 ( 1 – rp ) ( 1 + rp ) ------------------Δf ≤ f – f c < ------------------ Δf 2 2 ( 1 + rp ) ------------------- Δf ≤ f – f c 2 where 1 Δf = B ⋅ -------------------------------------------------------------------1 – r p + 4 ⁄ π ⋅ r p ⋅ arc cos 4 2 where α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and rp is the parameter Roll off factor. 804 BAND PASS COSINE ROLL OFF FILTER Band Pass Cosine Roll Off filter Filter with a cosine roll off frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll-off factor Simulation Determines whether or not the component is enabled 805 BAND PASS COSINE ROLL OFF FILTER Technical background Cosine Roll Off Filter has the following transfer function: ⎧ α ⎪ ⎪ f – fc – f1 ⎞ H ( f ) = ⎨ 0.5 ⋅ α 2 ⋅ 1 + cos ⎛ -----------------------⎝ r ⋅ Δf FWHM- ⋅ π⎠ ⎪ p ⎪ 0 ⎩ f – fc < f1 f 1 ≤ f – fc < f2 f 2 ≤ f – fc where α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, B is the parameter Bandwidth, and rp is the parameter Roll off factor. The parameters f1 and f2 are: 1–r f 1 = ------------p-B 2 0 ≤ rp ≤ 1 and 1+r f 1 = -------------p- B 2 806 0 ≤ rp ≤ 1 BAND PASS SQUARED COSINE ROLL OFF FILTER Band Pass Squared Cosine Roll Off filter Filter with a square cosine roll off frequency transfer function. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Frequency 10 GHz Hz, MHz, GHz [0,+INF[ 1.5 * bit rate Hz Hz, MHz, GHz [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 0.5 — — [0, 1] Name and description Default value Units Value range Enabled True — True, False Filter center frequency Bandwidth 3 dB filter bandwidth Insertion loss Insertion loss of the filter Depth Maximum attenuation value for the filter Roll off factor Simulation Determines whether or not the component is enabled 807 BAND PASS SQUARED COSINE ROLL OFF FILTER Technical background Square cosine roll off filter has the following transfer function: ⎧ α f – fc < f 1 ⎪ f – f – f ⎪ c 1⎞ H ( f ) = ⎨ 0.5 ⋅ α ⋅ 1 + cos ⎛ ----------------------- ⋅ π f1 ≤ f – fc < f2 ⎝ r ⋅ Δf ⎠ p ⎪ f2 ≤ f – fc ⎪ 0 ⎩ where α is the parameter Insertion loss, fc is the filter center frequency defined by the parameter Frequency, and rp is the roll off factor. The parameter Δ f is related to the filter bandwidth by: B Δf = ------------------------------------------------------------------------------2 1 + --- ⋅ arc cos ( 2 – 1 ) – 1 ⋅ r p π (2) where B is the parameter Bandwidth. 808 S PARAMETERS MEASURED FILTER S Parameters Measured filter Loads files with S Parameter measurements. You can load files directly from measurements by using the Touchstone (.s2p) format. Ports Name and description Port type Signal type Input Input Electrical Transmission Output Electrical Reflection Output Electrical Parameters Main Name and description Default value Default unit Units Value range User-defined frequency True — — True, False 0 GHz Hz, MHz, GHz [0, 1e+100] Name and description Default value Units Value range Filename (.s2p) Device.s2p — — Determines whether you can define the filter center frequency or use the value from the measurements Frequency User-defined filter center frequency Measurements Filename with the measured data 809 S PARAMETERS MEASURED FILTER Numerical Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Name and description Default value Units Value range Enabled True — True, False Determines the interpolation algorithm for the measured data Simulation Determines whether or not the component is enabled Graphs Name and description X Title Y Title Reflection - real part Frequency (Hz) Amplitude (a.u.) Reflection - imag part Frequency (Hz) Amplitude (a.u.) Transmission - real part Frequency (Hz) Amplitude (a.u.) Transmission - imag part Frequency (Hz) Amplitude (a.u.) Technical background The Touchstone Format is a common standard for S Parameter data. The model expects the .s2p file to be in the following general format (lines starting with the comment symbol '!' and blank lines are ignored): # freq_unit param_type data_form term_type term_val f1 s11a s11b s21a s21b s12a s12b s22a s22b f2 s11a s11b s21a s21b s12a s12b s22a s22b . . . fn s11a s11b s21a s21b s12a s12b s22a s22b where: 810 • freq_unit: Specifies the frequency units — can be Hz, kHz, MHz, or GHz. • param_type: Usually set to S to indicate S Parameter file. S PARAMETERS MEASURED FILTER • data_form: Either RI (for real imaginary), MA (for magnitude & angle) or DB (for magnitude in dB scale & angle). Indicates how the component should treat the pair of S Parameter values. • term_type: Termination type (R for real or Z for terminating impedance). Usually R. • term_val: Termination value (if R, then the value in Ohms, else a pair representing the impedance). The header is followed by the data. Each line has nine values — the frequency and the eight values representing four S Parameters. This model loads only the S11 and S21 (direct reflection and transmission). The following example was generated by a network analyzer. The units are in Hz and the data is in real and imaginary values. ! Network Analyzer ! Model 1 ! 16 Dec 1999 15:02:50 !Frequency S11 S21 S12 S22 # HZ S RI R 50 3000 2.17788E-1 0.24215E-1 -5.69091E0 4.64843E-1 3.02257E-2 0.33741E-2 -6.33483E-1 0.40252E-1 30029850 1.72088E-1 -1.57524E-1 -5.98193E0 -1.68359E0 4.33025E-2 1.31721E-2 -4.84573E-1 1.45126E-1 60029700 0.49133E-1 -2.12097E-1 -7.35302E0 -2.20703E0 5.24978E-2 1.82323E-2 -3.78585E-1 1.96167E-1 90029550 -4.32815E-2 -2.02163E-1 -8.36279E0 -2.04736E0 5.92289E-2 1.87740E-2 -2.99804E-1 1.91909E-1 120029400 -9.79766E-2 -1.74827E-1 -8.99023E0 -1.67724E0 6.32743E-2 1.8013E-2 -2.49618E-1 1.72729E-1 . . . The parameter User defined frequency determines if you can enter the center frequency. This means that the filter data is shifted from the measured center frequency to the user center frequency that you define by the parameter Frequency. 811 S PARAMETERS MEASURED FILTER Notes: 812 WDM Multiplexers Library This section contains information on the following WDM Multiplexers. Add and Drop • WDM Add • WDM Drop • WDM Add and Drop Demultiplexers • WDM Demux 1x2 • WDM Demux 1x4 • WDM Demux 1x8 • WDM Demux • WDM Demux ES • Ideal Demux • WDM Interleaver Demux Multiplexers • WDM Mux 2x1 • WDM Mux 4x1 • WDM Mux 8x1 • WDM Mux • WDM Mux ES • Ideal Mux • Nx1 Mux Bidirectional • AWG NxN • AWG NxN Bidirectional AWG 813 WDM MULTIPLEXERS LIBRARY Notes: 814 WDM ADD WDM Add Adds a WDM channel and a WDM signal. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30, 300000] Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 815 WDM ADD Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 816 WDM ADD Technical background The input signals are filtered by an optical filter and are combined in one signal. The first signal is filtered by an inverse filter. The optical filters can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 WDM Add subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 817 WDM ADD Notes: 818 WDM DROP WDM Drop Drops a WDM channel from a WDM signal. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30, 300000] Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 819 WDM DROP Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 820 WDM DROP Technical background The input signal is split into two signals. Each signal is filtered by an optical filter. The first signal is filtered by an inverse filter. The optical filters can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 WDM Drop subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 821 WDM DROP Notes: 822 WDM ADD AND DROP WDM Add and Drop WDM Add and Drop multiplexer. Equivalent to a subsystem based on the WDM Add and WDM Drop components. Ports Name and description Port type Signal type Input Input Optical Output (Drop) Output Optical Input (Add) Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Frequency 193.1 THz Hz, THz, nm [30, 300000] Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 823 WDM ADD AND DROP Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 824 WDM ADD AND DROP Technical background In the drop section, the input signal is divided in two signals. Each signal is filtered by an optical filter. An inverse filter filters the first signal. In the add section, the input signals are filtered by an optical filter and are combined in one signal. An inverse filter filters the first signal. The optical filters can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 WDM Add and drop subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 825 WDM ADD AND DROP Notes: 826 WDM DEMUX 1X2 WDM Demux 1x2 Demultiplexes two WDM signal channels. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 827 WDM DEMUX 1X2 Channels Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 828 WDM DEMUX 1X2 Technical background The input signal is split into two signals that are filtered by an optical filter. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Demultiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 829 WDM DEMUX 1X2 Notes: 830 WDM DEMUX 1X4 WDM Demux 1x4 Demultiplexes four WDM signal channels. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 831 WDM DEMUX 1X4 Channels Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 Ripple[2] Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate 832 WDM DEMUX 1X4 Noise Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 833 WDM DEMUX 1X4 Technical background The input signal is split into four signals that are filtered by an optical filter. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Demultiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 834 WDM DEMUX 1X8 WDM Demux 1x8 Demultiplexes eight WDM signal channels. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter 835 WDM DEMUX 1X8 Name and description Default value Default unit Units Value range Filter type Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] 193.5 THz Hz, THz, nm [30,3e5] 193.6 THz Hz, THz, nm [30,3e5] 193.7 THz Hz, THz, nm [30,3e5] 193.8 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Channels Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Frequency[4] Filter center frequency for channel 4 Frequency[5] Filter center frequency for channel 5 Frequency[6] Filter center frequency for channel 6 Frequency[7] Filter center frequency for channel 7 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 836 WDM DEMUX 1X8 Name and description Default value Units Value range Ripple[2] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Ripple[4] Additional loss of the filter for channel 4 Ripple[5] Additional loss of the filter for channel 5 Ripple[6] Additional loss of the filter for channel 6 Ripple[7] Additional loss of the filter for channel 7 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 837 WDM DEMUX 1X8 Technical background The input signal is split into eight signals that are filtered by an optical filter. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Demultiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 838 WDM DEMUX WDM Demux Demultiplexes a user-defined number of WDM signal channels. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default unit Units Value range Number of output ports 8 — — [2, 1000] Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter 839 WDM DEMUX Name and description Default value Default unit Units Value range Filter type Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] 193.5 THz Hz, THz, nm [30,3e5] 193.6 THz Hz, THz, nm [30,3e5] 193.7 THz Hz, THz, nm [30,3e5] 193.8 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Channels Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Frequency[4] Filter center frequency for channel 4 Frequency[5] Filter center frequency for channel 5 Frequency[6] Filter center frequency for channel 6 Frequency[7] Filter center frequency for channel 7 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 840 WDM DEMUX Name and description Default value Units Value range Ripple[2] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Ripple[4] Additional loss of the filter for channel 4 Ripple[5] Additional loss of the filter for channel 5 Ripple[6] Additional loss of the filter for channel 6 Ripple[7] Additional loss of the filter for channel 7 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 841 WDM DEMUX Technical background The input signal is split into N signals, where N is the number of output ports. The Signals are filtered by an optical filter. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Demultiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 842 WDM DEMUX ES WDM Demux ES Demultiplexes a user-defined number of WDM signal channels. The center frequencies of the internal filters are equally spaced (ES). Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Default value Default unit Units Value range Number of output ports 8 — — [2, 1000] Frequency 193.1 THz, Hz, nm [30,+INF[ 100 GHz, THz, Hz, nm ]-INF,+INF[ Hz, GHz, THz, nm [0,+INF[ Center frequency of the first filter Frequency spacing Frequency spacing between adjacent filters Bandwidth 3 dB filter bandwidth 10 GHz 843 WDM DEMUX ES Name and description Default value Default unit Units Value range Insertion loss 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Simulation Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical Background The WDM Demux ES is equivalent to the conventional WDM Demux component. However, the WDM Demux ES is easier to set up for WDM systems, since it requires only the filter center frequency and the spacing. 844 WDM INTERLEAVER DEMUX WDM Interleaver Demux An Interleaver Demux is a periodic optical filter that separates a combination of dense wavelength-division multiplexed (DWDM) signals. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Units Value range Number of channels 8 Frequency 193.1 THz, Hz, nm [30, +INF] 100 GHz, THz, Hz, nm [-INF, +INF] Hz, GHz, THz, nm [0, +INF] [2, 1000] Center frequency of the first filter Frequency spacing Frequency spacing between adjacent filters Bandwidth 10 GHz 0 dB [0, +INF] 100 dB [0, +INF] 3-dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Bessel [Rectangle, Gaussian, Bessel] 845 WDM INTERLEAVER DEMUX Name and description Default value Filter order 2 Default unit Units Value range [1, 1000] Order of the function when using Gaussian or Bessel filter type Technical Background This component demultiplexes equally spaced channels into two new sets of equally spaced channels. It makes DWDM systems whose intervals of channels are narrower (such as 100 GHz or 50 GHz) de-multiple into the systems whose intervals of channels are much thinner (such as 200 GHz or 100 GHz) [1]. References [1] S. Cao et all, "Interleaver Technology: Comparisons and Applications Requirements", OFC'03 Interleaver Workshop Review Paper, Formal Submission, JND ver 3.0, 062503, revised 091503. 846 IDEAL DEMUX Ideal Demux Demultiplexes a user-defined number of output WDM signal channels. This model is equivalent to an ideal splitter, since there is no power splitting and filtering. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Units Value range Number of output ports 2 — [2, 1000] Insertion loss 0 dB [0,+INF[ Insertion loss of the demux 847 IDEAL DEMUX Technical background The input signal is duplicated and attenuated. The subsystem is illustrated in Figure 1. Figure 1 Subsystem — duplicated and attenuated input signal 848 WDM MUX 2X1 WDM Mux 2x1 Multiplexes two WDM signal channels. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 849 WDM MUX 2X1 Channels Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 850 WDM MUX 2X1 Technical background The two input signals are filtered by an optical filter and are combined in one signal. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Multiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 851 WDM MUX 2X1 Notes: 852 WDM MUX 4X1 WDM Mux 4x1 Multiplexes four WDM signal channels. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type 853 WDM MUX 4X1 Channels Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 Ripple[2] Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate 854 WDM MUX 4X1 Noise Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 855 WDM MUX 4X1 Technical background The four input signals are filtered by an optical filter and are combined in one signal. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Multiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 856 WDM MUX 8X1 WDM Mux 8x1 Multiplexes eight WDM signal channels. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter 857 WDM MUX 8X1 Name and description Default value Default unit Units Value range Filter type Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] 193.5 THz Hz, THz, nm [30,3e5] 193.6 THz Hz, THz, nm [30,3e5] 193.7 THz Hz, THz, nm [30,3e5] 193.8 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Channels Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Frequency[4] Filter center frequency for channel 4 Frequency[5] Filter center frequency for channel 5 Frequency[6] Filter center frequency for channel 6 Frequency[7] Filter center frequency for channel 7 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 858 WDM MUX 8X1 Name and description Default value Units Value range Ripple[2] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Ripple[4] Additional loss of the filter for channel 4 Ripple[5] Additional loss of the filter for channel 5 Ripple[6] Additional loss of the filter for channel 6 Ripple[7] Additional loss of the filter for channel 7 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 859 WDM MUX 8X1 Technical background The eight input signals are filtered by an optical filter and are combined in one signal. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Multiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 860 WDM MUX WDM Mux Multiplexes a user-defined number of input WDM signal channels. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Number of input ports 8 — — [2,1000] Bandwidth 10 GHz Hz, GHz, THz, nm [0,+INF[ 0 dB — [0,+INF[ 100 dB — [0,+INF[ 3 dB filter bandwidth Insertion loss Insertion loss of the demux Depth Maximum attenuation value for the filter 861 WDM MUX Name and description Default value Default unit Units Value range Filter type Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Frequency[0] 193.1 THz Hz, THz, nm [30,3e5] 193.2 THz Hz, THz, nm [30,3e5] 193.3 THz Hz, THz, nm [30,3e5] 193.4 THz Hz, THz, nm [30,3e5] 193.5 THz Hz, THz, nm [30,3e5] 193.6 THz Hz, THz, nm [30,3e5] 193.7 THz Hz, THz, nm [30,3e5] 193.8 THz Hz, THz, nm [30,3e5] Name and description Default value Units Value range Ripple[0] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Channels Filter center frequency for channel 0 Frequency[1] Filter center frequency for channel 1 Frequency[2] Filter center frequency for channel 2 Frequency[3] Filter center frequency for channel 3 Frequency[4] Filter center frequency for channel 4 Frequency[5] Filter center frequency for channel 5 Frequency[6] Filter center frequency for channel 6 Frequency[7] Filter center frequency for channel 7 Ripple Additional loss of the filter for channel 0 Ripple[1] Additional loss of the filter for channel 1 862 WDM MUX Name and description Default value Units Value range Ripple[2] 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ 0 dB ]-INF,+INF[ Additional loss of the filter for channel 2 Ripple[3] Additional loss of the filter for channel 3 Ripple[4] Additional loss of the filter for channel 4 Ripple[5] Additional loss of the filter for channel 5 Ripple[6] Additional loss of the filter for channel 6 Ripple[7] Additional loss of the filter for channel 7 Simulation Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 863 WDM MUX Technical background The input signals are filtered by an optical filter and combined in one signal. The optical filter can be a Rectangle, Gaussian, or Bessel optical filter. The subsystem is illustrated in Figure 1. Figure 1 Multiplexer subsystem Defining crosstalk The level of crosstalk for both MUX and DEMUX components, is defined by bandwidth, ripple, and depth of the filter. These 3 factors will determine how much power, from neighboring channels, will act as crosstalk terms when calculating the performance of a specific channel. The most important parameter is depth, as it will play the most significant role in determining the power levels of the neighboring channels. 864 WDM MUX ES WDM Mux ES This component multiplexes a user-defined number of WDM signal channels. The center frequencies of the internal filters are equally spaced (ES). Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Number of input ports 8 — — [2,1000] Frequency 193.1 — THz, HZ, nm [30,+INF[ 100 — GHz, THz, Hz, nm ]-INF,+INF[ 10 GHz Hz, GHz, THz, nm [0,+INF[ Center frequency of the first filter Frequency spacing Frequency spacing between adjacent filters Bandwidth 3 dB filter bandwidth 865 WDM MUX ES Name and description Default value Default unit Units Value range Insertion loss 0 dB — [0,+INF[ 100 dB — [0,+INF[ Bessel — — Rectangle, Gaussian, Bessel 2 — — [1,1000] Name and description Default value Default unit Units Value range Enabled True — — True, False False — — True, False 128 GHz Hz, GHz, THz ]0,+INF[ Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Insertion loss of the demux Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Simulation Determines whether or not the component is enabled Resample Determines if the filter will down sample the signal bandwidth to the filter sample rate Sample rate New output signal sample rate Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical background The WDM Mux ES is equivalent to the conventional WDM Mux component. However, the WDM Mux ES is easier to set up for WDM systems, since it only requires the filter center frequency and the spacing. 866 IDEAL MUX Ideal Mux Multiplexers a user-defined number of input WDM signal channels. This model is equivalent to an ideal adder, since there is no power splitting and filtering. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Number of input ports 2 — [2,1000] Loss 0 dB [0,+INF] Insertion loss of the demux 867 IDEAL MUX Technical background The input signals are added and attenuated. The subsystem is illustrated in Figure 1. Figure 1 868 Ideal Multiplexer subsystem NX1 MUX BIDIRECTIONAL Nx1 Mux Bidirectional This component is bi-directional multiplexer or demultiplexer. It has a trapezoidal filter shape and arbitrary number of channels. Ports Name and description Port type Signal type Input Input Optical Input 1 Input Optical Input 2 Input Optical Output Output Optical Output 1 Input Optical Output 2 Input Optical Parameters Main Name and description Default value Number of input ports 2 — Value range [2, 1000] Defines the number of output ports for the component Frequency 193.1 Hz, THz, nm [30, 300000] 100 Hz, GHz, THz, nm [-10000, 10000] 0.1 Hz, GHz, THz, nm [0, 200] 0.01 Hz, THz, nm [100, 2000] 0 dB [0, +INF] Defines the first filter center frequency Frequency spacing Defines the spacing between frequency channels Bandwidth Defines the filter bandwidth Zero dB bandwidth Defines the trapezoidal filter zero dB bandwidth Insertion loss Component insertion loss at the operating wavelength 869 NX1 MUX BIDIRECTIONAL Name and description Default value — Value range Max. insertion loss 100 dB [0, +INF] 65 dB [0, +INF] Component insertion loss outside the operating bandwidth Return loss Component return loss at the operating wavelength Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Current lower limit for the graphs To Current upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 870 NX1 MUX BIDIRECTIONAL Graphs Name and description X Title Y Title Transmission Wavelength (m) Transmission Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: N E Out = ∑ EIn Ti ( f ) + EIn RL i j=1 E Out i = E In T i ( f ) + E Ini RL, i = [ 1, N ] where Ti(f) and is filter transmission for the input port i. N is the number of input ports. The filter transmission and return loss are given by T i ( f ) = 10 RL = 10 – IL -------20 H i 10 – RL ---------20 where IL is defined by the parameter Insertion loss and T(f) has the maximum value defined by the parameter Max. insertion loss. RL is defined by the parameter Return loss. The calculation equation for H(f) is the same used in the Trapezoidal Optical Filter component. If the parameter Calculate graphs is enabled, the component will generate a graph with the component transmission. 871 NX1 MUX BIDIRECTIONAL Notes: 872 AWG NXN AWG NxN This component simulates an ideal arrayed waveguide grating (AWG) component based on the use of optical filters to emulate the AWG response. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical ... Input Optical Output 1 Output Optical Output 2 Output Optical ... Output Optical Parameters Main Name and description Default value Size 8 Units Value range [2, 1000] Defines the number of output ports for the component Configuration Mux — Mux, Demux 193.1 Hz, THz, nm [30, 300000] 10 Hz, GHz, THz, nm [0, 200] -100 Hz, GHz, THz, nm [-10000, 10000] Defines whether the component works as a multiplexer or as a demultiplexer Frequency Defines the reference center frequency for the filter in the first port Bandwidth Defines the filter bandwidth Frequency spacing Defines the channel spacing 873 AWG NXN Name and description Default value Units Value range Insertion loss 0 dB [0, +INF] 100 dB [0,+INF[ Bessel — Rectangle, Gaussian, Bessel 2 — [1,1000] component insertion loss Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using Gaussian or Bessel filter type Simulation Name and description Default value Enabled True Default unit Units Value range [True, False] Determines whether or not the component is enabled Noise Name and description Default value Noise threshold Default unit Units Value range -100 dB [-INF, +INF] 3 dB [-INF +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical Background This component is based on the AWG NxN Bidirectional component. Parameter Configuration defines the order of the input and output ports, defining if the component works as a Mux or as a Demux. 874 AWG NXN BIDIRECTIONAL AWG NxN Bidirectional This bidirectional component simulates an ideal arrayed waveguide grating (AWG) component based on the use of optical filters to emulate the AWG response. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical ... Input Optical Output 1 Output Optical Output 2 Output Optical ... Output Optical Parameters Main Name and description Default value Size 8 Units Value range [2, 1000] Defines the number of input/output ports for the component Frequency 193.1 Hz, THz, nm [30, 300000] 10 Hz, GHz, THz, nm [0, 200] -100 Hz, GHz, THz, nm [-10000, 10000] 0 dB [0, +INF] Defines the reference center frequency for the filter in the first port Bandwidth Defines the filter bandwidth Frequency spacing Defines the channel spacing Insertion loss component insertion loss 875 AWG NXN BIDIRECTIONAL Name and description Default value Units Value range Return loss 65 dB [0, +INF] 100 dB [0,+INF[ Gaussian — Rectangle, Gaussian 2 — [1,1000] component return loss Depth Maximum attenuation value for the filter Filter type Internal filter type Filter order Order of the function when using the Gaussian filter type Simulation Name and description Default value Enabled True Default unit Units Value range [True, False] Determines whether or not the component is enabled Noise Name and description Default value Noise threshold Default unit Units Value range -100 dB [-INF, +INF] 3 dB [-INF +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Technical Background The AWG is an optical device based on interferential phenomena, and it has a periodic behavior in the wavelength domain. The input optical signals in each port are routed to a specific output port depending on the signal wavelength and the input port number. Upon the optical signals entering from a given input i and routed to an output port j, the AWG behaves like a passing-band periodical filter, its power transfer function having repeating at a fixed wavelength called free spectral range (FSR). The transfer function from the input i+1 to a given output j has the same shape as the previous transfer function of input i, but is shifted on the wavelength axis by an wavelength interval Δλ , another shift Δλ separates this second transfer function from the transfer function between the next input i+2 and the output j, and so on. The FSR can be defined in this component by: 876 AWG NXN BIDIRECTIONAL (1) FSR = N ⋅ Δλ Where N is the AWG Size parameter and Δλ is the wavelength (frequency) spacing. AWG can be fabricated which are able to act on "dense" comb of wavelengths, routing more contiguous wavelengths of the comb as if they were a single one. An parameter called coarseness C represents the number of contiguous wavelength channels belonging to the wavelength interval, Δλ , routable to the same output port. Considering i as the input port index, j as the output port index, and f as the channel index. We can define the AWG routing function as [1]: j = 1 + (i) i, j ∈ [ 1, M ]andf ∈ [ 1, ∞ ] (2) For example in case 1, we have four channels launched in input port 1 of an 4x4 AWG (see Figure 1). Figure 1 System layout case 1 The routing configuration in this case is: Case 1 - N = 4 ; Coarseness = 1; Signal at input port 1 and frequency 1, then J = 1 + (1 - 1 + (1 - 1)/1) mod 4 = 1; 877 AWG NXN BIDIRECTIONAL Signal at input port 1 and frequency 2, then J = 1 + (1 - 1 + (2 - 1)/1) mod 4 = 2; Signal at input port 2 and frequency 5, then J = 1 + (1 - 1 + (3 - 1)/1) mod 4 = 3; Signal at input port 2 and frequency 4, then J = 1 + (1 - 1 + (4 - 1)/1) mod 4 = 4; The output results can be seen at the figure below: Figure 2 Output signal at output port 1 (black), port 2 (red), port 3 (green), and port 4 (blue). In another example in case 2, we have 2 channels launched in input port 1 and 4 channels launched in input port 4 of a 6x6 AWG (see Figure 3). 878 AWG NXN BIDIRECTIONAL Figure 3 System layout case 2. The routing configuration in this case is: Case 2 - N = 6 ; Coarseness = 2; Signal at input port 1 and frequency 13, then J = 1 + (1 - 1 + (13 - 1)/2) mod 6 = 1; Signal at input port 1 and frequency 14, then J = 1 + (1 - 1 + (14 - 1)/2) mod 6 = 1; Signal at input port 4 and frequency 1, then J = 1 + (4 - 1 + (1 - 1)/2) mod 6 = 4; Signal at input port 4 and frequency 2, then J = 1 + (4 - 1 + (2 - 1)/2) mod 6 = 4; Signal at input port 4 and frequency 3, then J = 1 + (4 - 1 + (3 - 1)/2) mod 6 = 5 Signal at input port 4 and frequency 4, then J = 1 + (4 - 1 + (4 - 1)/2) mod 6 = 5; 879 AWG NXN BIDIRECTIONAL The output results can be seen at the figures below: Figure 4 Output signal at (a) output port 1, (b) port 4, (c)port 5. References [1] Maier, G., Martinelli, M., Pattavina, A., and Salvadori, E.. "Design and cost performance of the multistage WDM-PON access networks". IEEE J. of Lightwave Technology, 18:pp. 125-143. 880 Network Library This section contains information on the following network components. Optical Switches • Dynamic Y Select Nx1 Measured • Dynamic Y Switch 1xN Measured • Dynamic Y Switch 1xN • Dynamic Y Select Nx1 • Dynamic Space Switch Matrix NxM Measured • Dynamic Space Switch Matrix NxM • Optical Switch • Digital Optical Switch • Optical Y Switch • Optical Y Select • Ideal Switch 2x2 • Ideal Y Switch • Ideal Y Select • Ideal Y Switch 1x4 • Ideal Y Select 4x1 • Ideal Y Switch 1x8 • Ideal Y Select 8x1 • Ideal Y Select Nx1 • Ideal Y Switch 1xN • 2x2 Switch Bidirectional 881 NETWORK LIBRARY Frequency Conversion • 882 Ideal Frequency Converter DYNAMIC Y SELECT NX1 MEASURED Dynamic Y Select Nx1 Measured Y select with a user-defined mapping table for different switching events. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output Output Optical Parameters Main Name and description Units Value Default value Default unit Number of input ports 8 — — [2, 1000] Time constant 50 ns s, ms, ns [0,+INF[ 50 ns s, ms, ns [0,+INF[ False — — True, False range Switching time constant Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time 883 DYNAMIC Y SELECT NX1 MEASURED Name and description Mapping table filename Default value Default unit Table.dat — Units Value range — — Filename with the measured data Technical background Static solution The switch model allows for the selection of the number of input ports N. For the input ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude entering the input port number 'i' is Ei, then the electric field complex amplitude at the output port due to Ei is: E Output Input = Ei e j ( n i + jα i ) (1) When all input ports of the switch are used, the output complex amplitude at the output port is: E Output ⎧ Input j ( ni + jαi ) ⎫ ⎬ ∑ ⎨⎩ Ei e ⎭ i=1 N = (2) This sum includes all different wavelength contributions. 884 DYNAMIC Y SELECT NX1 MEASURED Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant τ . The parameter time constant τ is universal and is shared by all transient events. For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (3) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. File format The file format for the data with the map table is: n1,1 α 1, 1 n1,2 α 1, 2 n2,1 α 2, 1 n2,2 α 2, 2 α N, 1 nN,2 α N, 2 . . nN,1 where the first index is the input port (row) and the second index is the table number (1 or 2). Assuming a component with 3 input ports, and transient from port 1 to 3: 0 0 0 10 0 10 0 10 0 10 0 0 885 DYNAMIC Y SELECT NX1 MEASURED Notes: 886 DYNAMIC Y SWITCH 1XN MEASURED Dynamic Y Switch 1xN Measured Y switch with user-defined mapping table for different switching events. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Main Name and description Units Value Default value Default unit Number of output ports 8 — — [2, 1000] Time constant 50 ns s, ms, ns [0,+INF[ 50 ns s, ms, ns [0,+INF[ False — — True, False range Switching time constant Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time 887 DYNAMIC Y SWITCH 1XN MEASURED Name and description Mapping table filename Default value Default unit Table.dat — Units Value range — — Filename with the measured data Technical background Static solution The switch model allows for the selection of the number of output ports N. For the output ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude at the output port number 'i' is Ei, calculated from the electric field complex amplitude at the input port, Ei is: E Output Input = Ei e j ( n i + jα i ) (1) Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant universal and is shared by all transient events. 888 τ . The parameter time constant τ is DYNAMIC Y SWITCH 1XN MEASURED For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (2) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. File format The file format for the data with the map table is: n1,1 α 1, 1 n1,2 α 1, 2 n2,1 α 2, 1 n2,2 α 2, 2 α N, 1 nN,2 α N, 2 . . nN,1 where the first index is the output port (row) and the second index is the table number (1 or 2). Assuming a component with 3 output ports, and transient from port 3 to 1: 0 0 0 10 0 10 0 10 0 10 0 0 889 DYNAMIC Y SWITCH 1XN MEASURED Notes: 890 DYNAMIC Y SWITCH 1XN Dynamic Y Switch 1xN Y switch that allows you to control the different values for attenuation and phase values with transient effects when switching from different input ports. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Unit Value Default value Default unit Number of input ports 2 — — [2, 1000] Port before event 1 — — [1, 1000] 2 — — [1, 1000] 50 ns s, ms, ns [0,+INF[ False — — True, False 50 ns s, ms, ns [0,+INF[ range Port number to use before the event Port after event Port number to use after the event Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time Time constant Switching time constant 891 DYNAMIC Y SWITCH 1XN Table Name and description Default value Units Value range Real coeff. at selected port 1e-006 — ]-INF,+INF[ 1 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ Real coeff. equivalent to the phase at the selected port Imag coeff. at selected port Imag coeff. equivalent to the attenuation at the selected port Real coeff. at other ports Real coeff. equivalent to the phase at other ports Imag coeff. at other ports Imag coeff. equivalent to the attenuation at other ports Technical background Static solution The switch model allows for the selection of the number of input ports N. For the input ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude entering the input port number 'i' is Ei, then the electric field complex amplitude at the output port due to Ei is: E Output Input = Ei e j ( n i + jα i ) (1) 892 DYNAMIC Y SWITCH 1XN When all input ports of the switch are used, the output complex amplitude at the output port is: N E Output = ⎧ ∑ ⎨⎩ Ei Input e j ( n i + jα i ) ⎫ i=1 ⎬ ⎭ (2) This sum includes all different wavelength contributions. Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant τ . The parameter time constant τ is universal and is shared by all transient events. For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (3) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. Mapping table The mapping table is generated based on the values for the selected and unselected ports. You can select the values of the real and imag coefficients for the selected port and for the unselected ports. The models assumes that all unselected ports have the same phase and attenuation. For arbitrary values for these coefficients, use the equivalent measured component. 893 DYNAMIC Y SWITCH 1XN Notes: 894 DYNAMIC Y SELECT NX1 Dynamic Y Select Nx1 Y select that allows you to control the different values for attenuation and phase values with transient effects when switching from different output ports. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Main Name and description Units Value Default value Default unit Number of input ports 2 — — [2, 1000] Port before event 1 — — [1, 1000] 2 — — [1, 1000] 50 ns s, ms, ns [0,+INF[ False — — True, False 50 ns s, ms, ns [0,+INF[ range Port number to use before the event Port after event Port number to use after the event Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time Time constant Switching time constant 895 DYNAMIC Y SELECT NX1 Table Name and description Default value Units Value range Real coeff. at selected port 1e-006 — ]-INF,+INF[ 1 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ Real coeff. equivalent to the phase at the selected port Imag coeff. at selected port Imag coeff. equivalent to the attenuation at the selected port Real coeff. at other ports Real coeff. equivalent to the phase at other ports Imag coeff. at other ports Imag coeff. equivalent to the attenuation at other ports Technical background Static solution The switch model allows for the selection of the number of output ports N. For the input ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude at the output port number 'i' is Ei, calculated from the electric field complex amplitude at the input port, Ei is: E Output Input = Ei e j ( n i + jα i ) (1) 896 DYNAMIC Y SELECT NX1 Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant τ . The parameter time constant τ is universal and is shared by all transient events. For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (2) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. Mapping table The mapping table is generated based on the values for the selected and unselected ports. You can select the values of the real and imag coefficients for the selected port and for the unselected ports. The models assume that all unselected ports have the same phase and attenuation. For arbitrary values for these coefficients, use the equivalent measured component. 897 DYNAMIC Y SELECT NX1 Notes: 898 DYNAMIC SPACE SWITCH MATRIX NXM MEASURED Dynamic Space Switch Matrix NxM Measured Space switch matrix with a user-defined mapping table for different switching events. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical 899 DYNAMIC SPACE SWITCH MATRIX NXM MEASURED Parameters Main Name and description Unit Value Default value Default unit Number of input ports 8 — — [1, 1000] Number of output ports 8 — — [1, 1000] Time constant 50 ns s, ms, ns [0,+INF[ 50 ns s, ms, ns [0,+INF[ False — — True, False Table.dat — — — range Switching time constant Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time Mapping table filename Filename with the measured data 900 DYNAMIC SPACE SWITCH MATRIX NXM MEASURED Technical background Static solution The switch model allows for the selection of the number of input ports N and output ports M. For the input ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude entering the input port number 'i' is Ei, then the electric field complex amplitude at the output port due to Ei is: E Output Input = Ei e j ( n i + jα i ) (1) When all input ports of the switch are used, the output complex amplitude at each output port is: E Output N = ⎧ ∑ ⎨⎩ Ei i=1 Input e j ( n i + jα i ) ⎫ ⎬ ⎭ (2) This sum includes all different wavelength contributions. 901 DYNAMIC SPACE SWITCH MATRIX NXM MEASURED Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant τ . The parameter time constant τ is universal and is shared by all transient events. For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (3) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. File format The file format for the data with the map table is: n1,1 α 1, 1 n1,2 α 1, 2 ... n1,1,M α 1, 1, M n1,2,M α 1, 2, M n2,1 α 2, 1 n2,2 α 2, 2 ... n2,1,M α 2, 1, M n2,2,M α 2, 2, M α N, 1 nN,2 α N, 2 ... nN,1,M α N , 1, M nN,2,M α N , 2, M .. .. nN,1 where the first index is the input port (row), the second index is the table number (1 or 2), and the third index is the output port. This means that there is one row for each input port and 4 columns for each output port. Assuming a component with 3 input and output ports, and transient from port 1 to 3: 0 0 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 10 0 0 902 DYNAMIC SPACE SWITCH MATRIX NXM Dynamic Space Switch Matrix NxM Space switch matrix that allows you to control the different values for attenuation and phase values with transient effects when switching from different input and output ports. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical 903 DYNAMIC SPACE SWITCH MATRIX NXM Parameters Main Name and description Unit Value Default value Default unit Number of input ports 8 — — [2, 1000] Number of output ports 8 — — [2, 1000] Input port before event 1 — — [1, 1000] 1 — — [1, 1000] 2 — — [1, 1000] 2 — — [1, 1000] 50 ns s, ms, ns [0,+INF[ False — — True, False 50 ns s, ms, ns [0,+INF[ range Port number to use before the event Input port after event Port number to use after the event Output port before event Port number to use before the event Output port after event Port number to use after the event Switching event time Time instant when the switching event occurs Repeat events Determines if the events will be repeated for each event time Time constant Switching time constant Table Name and description Default value Units Value range Real coeff. at selected port 1e-006 — ]-INF,+INF[ 1 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ 1e-006 — ]-INF,+INF[ Real coeff. equivalent to the phase at selected port Imag coeff. at selected port Imag coeff. equivalent to the attenuation at selected port Real coeff. at other ports Real coeff. equivalent to the phase at other ports Imag coeff. at other ports Imag coeff. equivalent to the attenuation at other ports 904 DYNAMIC SPACE SWITCH MATRIX NXM Technical background Static solution The switch model allows for the selection of the number of input ports N and output ports M. For the input ports i = 1…N, you can select the complex values of a mapping table: i=1 n1 + j × α1 i=2 n2 + j × α2 i=3 n3 + j × α3 . . . nN + j × αN i=N where j = ( –1 ) If the light electric field complex amplitude entering the input port number 'i' is Ei, then the electric field complex amplitude at the output port due to Ei is: E Output Input = Ei e j ( n i + jα i ) (1) When all input ports of the switch are used, the output complex amplitude at each output port is: E Output N = ⎧ ∑ ⎨⎩ Ei i=1 Input e j ( n i + jα i ) ⎫ ⎬ ⎭ (2) This sum includes all different wavelength contributions. 905 DYNAMIC SPACE SWITCH MATRIX NXM Transients This type of switch is characterized by switching time with a time constant. Mathematically, a switching event is a replacement of one mapping table, T1, with a different one, T2. To a first order approximation, the change from { n i + j × α i } T1 to { n i + j × α i } T2 resembles a charging process of a linear capacitor through a linear resistor. It has an exponential time behavior, with a time constant τ . The parameter time constant τ is universal and is shared by all transient events. For a switching event that takes place at time t0, the real part of a mapping matrix element will change as: n i ( t ) = ni T1 × exp ( – ( t – t 0 ) ⁄ τ ) + n i T2 × { 1 – exp ( – ( t – t 0 ) ⁄ τ ) } (3) t0 is the parameter Switching event time. The parameter Repeat events allows you to generate multiple switching events. For example, changing the map table from 1 to 2 and vice versa. Mapping table The mapping table is generated based on the values for the selected and unselected ports. You can select the values of the real and imag coefficients for the selected port and for the unselected ports. The models assume that all unselected ports have the same phase and attenuation. For arbitrary values for these coefficients, use the equivalent measured component. 906 OPTICAL SWITCH Optical Switch Simulates a non-ideal switch 2x2. Ports Name and description Port type Signal type Input1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Value range Phase shift Zero — Zero, pi Additional loss 0 dB [0, 1e100] Technical background The optical switch routes the optical signals at input port 1 and 2 to the two output ports, according to the parameter phase shift described as follows: • If the phase shift is 0, then the optical signal at input 1 is passed to output 2 and the optical signal at input 2 is passed to output 1 (see Figure 1). 907 OPTICAL SWITCH • If the phase shift is π , then the optical signal at input 2 is passed to output 2 and the optical signal at input 1 is passed to output 1 (Figure 1). Figure 1 Switch behavior The following equations describe the switch behavior: E 1out E 2out = α⋅ m 11 m 12 m 21 m 22 ⋅ E 1in E 2in where E1in and E2in are the input signals at input port 1 and 2 respectively. m 11 = ( 1 – cc ) ⋅ exp ( j ⋅ φ ) – cc (4) m 12 = 1 – cc ⋅ j ⋅ cc ⋅ ( exp ( j ⋅ φ ) + 1 ) (5) m 21 = 1 – cc ⋅ j ⋅ cc ⋅ ( exp ( j ⋅ φ ) + 1 ) (6) m22 = ( 1 – cc ) ⋅ – cc ⋅ exp ( j ⋅ φ ) (7) where the coupling coefficient, cc, is 0.5, additional loss. 908 φ is the phase shift parameter, and α is the DIGITAL OPTICAL SWITCH Digital Optical Switch Simulates a non-ideal switch 2x2 with a control signal. Ports Name and description Port type Signal type Control Input Binary Input1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Value range Additional loss 0 dB [0, 1e100] 909 DIGITAL OPTICAL SWITCH Technical background The digital optical switch routes the optical signals at input port 1 and 2 to the two output ports, according to the control signal described as follows: • If the control signal is 0, then the optical signal at input 1 is passed to output 1 and the optical signal at input 2 is passed to output 2. • If the control signal is 1, then the optical signal at input 2 is passed to output 1 and the optical signal at input 1 is passed to output 2. The working behavior of this component is similar to the optical switch component. When the control signal is 0, internally the phase shift is set at π , and when the control signal is 1, the phase shift is set at 0. 910 OPTICAL Y SWITCH Optical Y Switch Simulates a non-ideal optical switch 1x2. Ports Name and description Port type Signal type Control Input Binary Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Default unit Value range Insertion loss 0 dB [0, 1e100] Crosstalk 1 30 dB [0, 1e100] Crosstalk 2 30 dB [0, 1e100] Phase shift 1 90 deg [-1e50, 1e50] Phase shift 2 90 deg [-1e50, 1e50] 911 OPTICAL Y SWITCH Technical background The digital optical 1x2 switch routes the input signal to one of two output ports, including crosstalk and phase shift between the two input signals. The parameters responsible for crosstalk between the two output signals are crosstalk 1 and crosstalk 2. The phase shift is specified by phase shift 1 and phase shift 2. This model has two modes of operation: • If the control is 0, then the optical signal at input is routed to output 1 (see Figure 1). • If the control is 1, then the optical signal at input is routed to output 2 (see Figure 1). Figure 1 912 Switch behavior OPTICAL Y SELECT Optical Y Select Simulates a non-ideal optical switch 2x1. Ports Name and description Port type Signal type Control Input Binary Input1 Input Optical Input 2 Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Insertion loss 0 dB [0, 1e100] Crosstalk 1 30 dB [0, 1e100] Crosstalk 2 30 dB [0, 1e100] Phase shift 1 90 deg [-1e50, 1e50] Phase shift 2 90 deg [-1e50, 1e50] 913 OPTICAL Y SELECT Technical background The digital optical 2x1 switch selects one of the two input signals and the route to the output port, including crosstalk and phase shift between the two input signals. The parameters responsible for crosstalk between the input signals are crosstalk 1 and crosstalk 2. The phase shift is specified by phase shift 1 and phase shift 2. This model has two modes of operation: • If the control is 0, then the optical signal at input 1 is passed to the output (see Figure 1). • If the control is 1, then the optical signal at input 2 is passed to the output (see Figure 1). Figure 1 914 Switch behavior IDEAL SWITCH 2X2 Ideal Switch 2x2 Simulates an ideal switch 2x2. Ports Name and description Port type Signal type Control Input Binary Input1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 915 IDEAL SWITCH 2X2 Technical background The ideal optical 2x2-switch routes the optical signals at input port 1 and 2 to the two output ports according with the control signal. The ideal 2x2 switch has two modes of operation: • If the control is 0, then the optical signal at input 1 is passed to output 1 and the optical signal at input 2 is passed to output 2 (see Figure 1). • If the control is 1, then the optical signal at input 2 is passed to output 1 and the optical signal at input 1 is passed to output 2 (see Figure 1). Figure 1 916 Switch behavior IDEAL Y SWITCH Ideal Y Switch Simulates an ideal optical 1x2 switch. Ports Name and description Port type Signal type Control Input Binary Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 917 IDEAL Y SWITCH Technical background The ideal optical 1x2 switch routes a signal in the input port to one of two output ports. The ideal 2x1 switch has two modes of operation as follows: • If the control is 0, then the optical signal at input 1 is passed to output 1 (see Figure 1). • If the control is 1, then the optical signal at input 2 is passed to output 2 (see Figure 1). Figure 1 918 Switch behavior IDEAL Y SELECT Ideal Y Select Simulates an ideal optical select switch. Ports Name and description Port type Signal type Control Input Binary Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 919 IDEAL Y SELECT Technical background The ideal Y select switch has two modes of operation: • If the control is 0, then the optical signal at input 1 is passed to the output (see Figure 1). • If the control is 1, then the optical signal at input 2 is passed to the output (see Figure 1). Figure 1 920 Switch behavior IDEAL Y SWITCH 1X4 Ideal Y Switch 1x4 Simulates an ideal optical 1x4 switch. Ports Name and description Port type Signal type Control Input Binary Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 921 IDEAL Y SWITCH 1X4 Technical background The ideal optical 1x4 switch routes a signal in the input port to one of four output ports. The ideal 1x4 switch has four states of operation, as follows: • If the control is 00, then the optical signal at input is passed to output 1 (see Figure 1). • If the control is 01, then the optical signal at input is passed to output 2 (see Figure 1). • If the control is 10, then the optical signal at input is passed to output 3 (see Figure 1). • If the control is 11, then the optical signal at input is passed to output 4 (see Figure 1). Figure 1 922 Two possible working states of the 4x1 switch IDEAL Y SELECT 4X1 Ideal Y Select 4x1 Simulates an ideal optical switch 4x1. Ports Name and description Port type Signal type Control Input Binary Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Output Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 923 IDEAL Y SELECT 4X1 Technical background The ideal Y select 4x1 switch has four states of operation: • If the control is 00, then the optical signal at input 1 is passed to out (see Figure 1). • If the control is 01, then the optical signal at input 2 is passed to out (see Figure 1). • If the control is 10, then the optical signal at input 3 is passed to out (see Figure 1). • If the control is 11, then the optical signal at input 4 is passed to out (see Figure 1). Figure 1 924 Two possible working states of the 4x1 switch IDEAL Y SWITCH 1X8 Ideal Y Switch 1x8 Simulates an ideal optical 1x8 switch. Ports Name and description Port type Signal type Control Input Binary Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Output 5 Output Optical Output 6 Output Optical Output 7 Output Optical Output 8 Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 925 IDEAL Y SWITCH 1X8 Technical background The ideal optical 1x8-switch routes a signal in the input port to one of eight output ports (see Figure 1). Figure 1 One possible working state of the 1x8 switch Table 1 displays the switching states for the eight output ports. Table 1 Switching states — output ports Control Output 1 Output 2 Output 3 Output 4 Output 5 Output 6 Output 7 Output 8 000 X — — — — — — — 001 — X — — — — — — 010 — — X — — — — — 011 — — — X — — — — 100 — — — — X — — — 101 — — — — — X — — 110 — — — — — — X — 111 — — — — — — — X 926 IDEAL Y SELECT 8X1 Ideal Y Select 8x1 Simulates an ideal optical switch 8x1. Ports Name and description Port type Signal type Control Input Binary Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Input 5 Input Optical Input 6 Input Optical Input 7 Input Optical Input 8 Input Optical Output Output Optical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled 927 IDEAL Y SELECT 8X1 Technical background The ideal optical 8x1-switch routes one of the 8 input signals to the output port. Figure 1 One possible working state of the 8x1 switch Table 2 displays the switching states for the eight input ports. Table 2 Switching states — input ports Control Input 1 Input 2 Input 3 Input 4 Input 5 Input 6 Input 7 Input 8 000 X — — — — — — — 001 — X — — — — — — 010 — — X — — — — — 011 — — — X — — — — 100 — — — — X — — — 101 — — — — — X — — 110 — — — — — — X — 111 — — — — — — — X 928 IDEAL Y SELECT NX1 Ideal Y Select Nx1 Simulates an ideal optical switch with a variable number of input ports. Ports Name and description Port type Signal type Control Input Binary Input 1 Input Optical Input 2 Input Optical Output Output Optical Parameters Simulation Name and description Default value Units Value range Number of input ports 2 — [2, 1000] Enabled True — True, False Determines whether or not the component is enabled 929 IDEAL Y SELECT NX1 Technical background The number of input ports for the Nx1 switch is given by the number of input ports parameter. The bit sequence length of control signals must be enough for the correct use of the switch. The minimum number of bits is: n b = log 2 ( N in ) where nb is the number of bits and Nin is the number of input ports. The control signal specifies which input port will have the optical signal routed to the output port. 930 IDEAL Y SWITCH 1XN Ideal Y Switch 1xN Simulates an ideal optical 1xN switch with a variable number of output ports. Ports Name and description Port type Signal type Control Input Binary Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Simulation Name and description Default value Units Value range Number of output ports 2 — [2, 1000] Enabled True — True, False Determines whether or not the component is enabled 931 IDEAL Y SWITCH 1XN Technical background The control signal must be long enough for the correct use of the switch. The minimum number of bits is: n b = log 2 ( N out ) where nb is the number of bits and Nout is the number of output ports. The control signal specifies which output port will have the optical signal routed at the input port. 932 2X2 SWITCH BIDIRECTIONAL 2x2 Switch Bidirectional This component is bi-directional optical 2x2 switch. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Parameters Main Name and description Default value Switch state Bar Default unit Value range [Bar, Cross] Defines whether the component is using bar or cross mode Isolation 0 dB [0, +INF] 55 dB [0, +INF] 65 dB [0, +INF] Component isolation Insertion loss Component insertion loss Return loss Component return loss 933 2X2 SWITCH BIDIRECTIONAL Simulation Name and description Default value Enabled True Default unit Units Value range [True, False] Determines whether or not the component is enabled Technical Background The signal input electrical field for both polarizations for each output port calculation depends on the parameter Switch state: Bar: E Out 1 = E In3 IL + E In 4 IS + E In1 RL E Out 2 = E In4 IL + E In 3 IS + E In2 RL (1) E Out 3 = E In1 IL + E In 2 IS + E In3 RL E Out 4 = E In2 IL + E In 1 IS + E In4 RL Cross: E Out 1 = E In4 IL + E In 3 IS + E In1 RL E Out 2 = E In3 IL + E In 4 IS + E In2 RL (1) E Out 3 = E In2 IL + E In 1 IS + E In3 RL E Out 4 = E In1 IL + E In 2 IS + E In4 RL where IL, IS and RL are the insertion loss, isolation and return losses, respectively. IL = 10 IS = 10 – IL -------20 – IS -------20 RL = 10 934 – RL ---------20 IDEAL FREQUENCY CONVERTER Ideal Frequency Converter Simulates an ideal frequency converter. Ports Name and description Port type Signal type Optical Input Optical Optical Output Optical Parameters Main Name and description Default value Default unit Value range Frequency offset 100 GHz [-1e6, 1e6 ] Shift band True — True, False Name and description Default value Units Value range Enabled True — True, False Simulation Determines whether or not the component is enabled 935 IDEAL FREQUENCY CONVERTER Technical background The ideal frequency converter shifts the optical signal spectrum by the amount (frequency offset). There are two modes of operation: Δf • If the shift band parameter is true, then the center frequency is changed and the complex amplitude of the sampled electrical field remains unchanged (see Figure 1). • If shift band parameter is false, a cyclic shift is performed (see Figure 1). The complex amplitudes are changed according to: E out ( t ) = E in ( t ) ⋅ exp ( 2 ⋅ π ⋅ Δf ⋅ t ) For parameterized and noise bins signals, there is only one mode of operation — shift band true. Figure 1 936 Ideal frequency converter behavior: (a) input signal, (b) output signal – shift band false and (c) output signal – shift band true Passives Library This section contains information on the following passives. Electrical • Electrical Phase Shift • Electrical Signal Time Delay Attenuators • Electrical Attenuator Couplers • 90 Degree Hybrid Coupler • 180 Degree Hybrid Coupler DC Blockers • DC Block Splitters • Splitter 1x2 • Splitter 1xN Combiners • Combiner 2x1 • Combiner Nx1 937 PASSIVES LIBRARY Measured Components • 1 Port S Parameters • 2 Port S Parameters • 3 Port S Parameters • 4 Port S Parameters Optical • Phase Shift • Time Delay Attenuators • Optical Attenuator • Attenuator Bidirectional Connectors • Connector • Connector Bidirectional • Spatial Connector Reflectors • Reflector Bidirectional Taps • Tap Bidirectional Measured Components • Luna Technologies OVA Measurement • Measured Component Multimode 938 • Spatial Aperture • Thin Lens • Vortex Lens PASSIVES LIBRARY Couplers • X Coupler • Pump Coupler Co-Propagating • Pump Coupler Counter-Propagating • Coupler Bidirectional • Pump Coupler Bidirectional Power Splitters • Power Splitter 1x2 • Power Splitter 1x4 • Power Splitter 1x8 • Power Splitter • 1xN Splitter Bidirectional Power Combiners • Power Combiner 2x1 • Power Combiner 4x1 • Power Combiner 8x1 • Power Combiner Polarization • Linear Polarizer • Circular Polarizer • Polarization Attenuator • Polarization Delay • Polarization Phase Shift • Polarization Combiner • Polarization Controller • Polarization Rotator • Polarization Splitter • Time DelayPMD Emulator • Polarization Combiner Bidirectional • Polarization Waveplate 939 PASSIVES LIBRARY Isolators • Isolator • Ideal Isolator • Isolator Bidirectional Circulators 940 • Circulator • Ideal Circulator • Circulator Bidirectional ELECTRICAL PHASE SHIFT Electrical Phase Shift Adds a time phase advance/delay to the optical signal input. The component also allows the user to define a phase slope that is linear with frequency. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Units Value range Phase shift 0 deg, rad ]-INF,+INF[ False — True, False 0 deg/oct, rad/oct ]-INF,+INF[ Sample rate / 2 Hz, MHz, GHz [0, 1e100] Name and description Default value Units Value range Enabled True — True, False Phase shift to apply to the signal Slope Determines whether or not the phase slope is enabled Phase slope Phase slope to apply to the signal Start frequency Phase slope will be applied to frequencies greater than the start frequency value. Simulation Determines whether or not the component is enabled 941 ELECTRICAL PHASE SHIFT Notes: 942 ELECTRICAL SIGNAL TIME DELAY Electrical Signal Time Delay Adds a time delay to the electrical signal input. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Delay 0 s s, ms, ns [0,+INF[ Name and description Default value Units Value range Enabled True — True, False True — True, False Delay to apply to the signal input Simulation Determines whether or not the component is enabled Discrete delay If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value 943 ELECTRICAL SIGNAL TIME DELAY Notes: 944 ELECTRICAL ATTENUATOR Electrical Attenuator Attenuates the electrical signal input. Ports Name and description Port type Signal type Input Input Electrical Output Output Electrical Parameters Main Name and description Default value Default unit Units Value range Attenuation 0 dB dB [0,+INF[ Name and description Default value Units Value range Enabled True — True, False Attenuation to apply to the signal input Simulation Determines whether or not the component is enabled 945 ELECTRICAL ATTENUATOR Notes: 946 90 DEGREE HYBRID COUPLER 90 Degree Hybrid Coupler This component is a 90 degree hybrid coupler for combining electrical signals. It allows the user to define gain and phase balance. Typical applications include mixers, power combiners and modulators. Ports Name and description Port type Signal type Input 1 Input Electrical Input 2 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,1e100] 0 dB [-1e100, 1e100] 0 deg [-1e100, 1e100] Loss applied to the signal after coupling Gain balance The difference in dB between the two output ports of the coupler. Phase balance The additional phase difference between the two output ports of the coupler 947 90 DEGREE HYBRID COUPLER Technical background The s-parameters for the coupler are: S O1 I 1 = [ – 3dB – α + 0.5 × G ] ∠0° (1) S O2 I 1 = [ – 3dB ( – α – 0.5 × G ) ] ∠( – 90° – φ ) (2) Where α is the insertion loss (dB), G is the gain balance (dB) and φ is the phase balance between output ports. 948 180 DEGREE HYBRID COUPLER 180 Degree Hybrid Coupler This component is a 180 degree hybrid coupler for combining electrical signals. It allows the user to define gain and phase balance. Typical applications include mixers, power combiners and modulators. Ports Name and description Port type Signal type Input 1 Input Electrical Input 2 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,1e100] 0 dB [-1e100, 1e100] 0 deg [-1e100, 1e100] Loss applied to the signal after coupling Gain balance The difference in dB between the two output ports of the coupler. Phase balance The additional phase difference between the two output ports of the coupler 949 180 DEGREE HYBRID COUPLER Technical background The s-parameters for the coupler are: S O1 I 1 = [ – 3dB – α + 0.5 × G ] ∠0° S O2 I 1 = [ – 3dB ( – α – 0.5 × G ) ] ∠( – 180° – φ ) Where α is the insertion loss (dB), G is the gain balance (dB) and φ is the phase balance between output ports. 950 (1) (2) DC BLOCK DC Block This component blocks the DC voltage from the electrical input signal. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Parameters Simulation Name and description Default value Units Value range Enabled True — True, False Determines whether or not the component is enabled Technical background This component blocks the DC component from the input signal by removing its mean value. 951 DC BLOCK Notes: 952 SPLITTER 1X2 Splitter 1x2 This component splits evenly the signal input power to two output ports. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,+INF[ Additional loss applied to the signal Technical background The s-parameters for the splitter are: S Oi I1 = [ – 3dB – α ] ∠0° (1) Where α is the parameter insertion loss (dB) and i is the output port index. 953 SPLITTER 1X2 Notes: 954 SPLITTER 1XN Splitter 1xN This component splits evenly the signal input power to N output ports. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Number of output ports 2 — [2, 1000] 0 dB [0,+INF[ The number of output ports of the component Loss Additional loss applied to the signal 955 SPLITTER 1XN Technical background The s-parameters for the splitter are: 1- – α ∠0° S Oi I 1 = 10 log --N (1) Where α is the parameter insertion loss (dB), N is the number of output ports and i is the output port index. 956 COMBINER 2X1 Combiner 2x1 This component combines evenly two input signals into a single output port. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,+INF[ Additional loss applied to the signal 957 COMBINER 2X1 Technical background The s-parameters for the combiner are: S O1 I i = [ – 3dB – α ] ∠0° (1) Where α is the parameter insertion loss (dB), N is the number of input ports and i is the input port index. 958 COMBINER NX1 Combiner Nx1 This component combines evenly N input signals into a single output port. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Number of input ports 2 — [2, 1000] 0 dB [0,+INF[ The number of input ports of the component Loss Additional loss applied to the signal 959 COMBINER NX1 Technical background The s-parameters for the combiner are: 1- – α ∠0° S O1 I i = 10 log --N (1) Where α is the parameter insertion loss (dB), N is the number of input ports and i is the input port index. 960 1 PORT S PARAMETERS 1 Port S Parameters This component loads a Touchstone type file containing 1 port s-parameters data. Ports Name and description Port type Signal type Input 1 Input Electrical Output 1 Output Electrical Parameters Main Name and description Default value Units Value range Filename (.s1p) Device.s1p — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Name and description Default value Units Value range Calculate graphs False — True, False Touchstone type file containing 1 port s-parameters data. Numerical Determines the interpolation algorithm for the data Graphs Define whether to calculate graphs or not 961 1 PORT S PARAMETERS Simulation Name and description Default value Units Value range Enabled True — True, False False — True, False 64 — [1, 100e6] Determines whether or not the component is enabled Digital filter Determines whether or not the component will use a digital filter to process individual samples Digital filter order The numbers of coefficients for the time domain filter estimation Technical background This component loads a file that describes the small signal scattering matrix, or s parameters, of a device. Data structure of the Touchstone file consists of a header part and a data part (Refer to S Parameters Measured filter for a description of the file format). The content of the file is text data, which is ready to be read with a general text editor. 962 2 PORT S PARAMETERS 2 Port S Parameters This component loads a Touchstone type file containing 2 port s-parameters data, including noise figure data. Ports Name and description Port type Signal type Input 1 Input Electrical Input 2 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Parameters Main Name and description Default value Units Value range Filename (.s2p) Device.s2p — — True — True, false 4e-21 A/Hz-1, W/Hz, mW/Hz, dBm/Hz [0,+INF] Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Touchstone type file containing 2 port s-parameters data. Include Noise Defines whether the noise will be included in the output Input noise density Minimum input noise Numerical Determines the interpolation algorithm for the data 963 2 PORT S PARAMETERS Graphs Name and description Default value Units Value range Calculate graphs False — True, False Define whether to calculate graphs or not Simulation Name and description Default value Units Value range Enabled True — True, False False — True, False 64 — [1, 100e6] Determines whether or not the component is enabled Digital filter Determines whether or not the component will use a digital filter to process individual samples Digital filter order The numbers of coefficients for the time domain filter estimation Noise Name and description Default value Default unit Units Value range Add noise to signal False — — True, False Name and description Default value Units Value range Generate random seed True — True, False 0 — [0,4999] Determines whether or not the component will add the signal and noise components Random numbers Determines if the seed is automatically defined and unique Random seed index User-defined seed index for noise generation 964 2 PORT S PARAMETERS Technical background This component loads a file that describes the small signal scattering matrix, or s parameters, of a device. Data structure of the Touchstone file consists of a header part and a data part (Refer to S Parameters Measured filter for a description of the file format). The content of the file is text data, which is ready to be read with a general text editor. This component adds thermal noise to the signal output. The value of the thermal noise is calculated from the input SNR and the minimum noise figure from the parameters provided in the s2p file Since OptiSystem can have noiseless electrical signals, the parameter Input noise density assures a minimum value for the noise floor at the input signal. 965 2 PORT S PARAMETERS Notes: 966 3 PORT S PARAMETERS 3 Port S Parameters This component loads a Touchstone type file containing 3 port s-parameters data. Ports Name and description Port type Signal type Input 1 Input Electrical Input 2 Input Electrical Input 3 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Output 3 Output Electrical Parameters Main Name and description Default value Units Value range Filename (.s3p) Device.s3p — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Touchstone type file containing 3 port s-parameters data. Numerical Determines the interpolation algorithm for the data 967 3 PORT S PARAMETERS Graphs Name and description Default value Units Value range Calculate graphs False — True, False Define whether to calculate graphs or not Simulation Name and description Default value Units Value range Enabled True — True, False False — True, False 64 — [1, 100e6] Determines whether or not the component is enabled Digital filter Determines whether or not the component will use a digital filter to process individual samples Digital filter order The numbers of coefficients for the time domain filter estimation Technical background This component loads a file that describes the small signal scattering matrix, or s parameters, of a device. Data structure of the Touchstone file consists of a header part and a data part (Refer to S Parameters Measured filter for a description of the file format). The content of the file is text data, which is ready to be read with a general text editor. 968 4 PORT S PARAMETERS 4 Port S Parameters This component loads a Touchstone type file containing 4 port s-parameters data. Ports Name and description Port type Signal type Input 1 Input Electrical Input 2 Input Electrical Input 3 Input Electrical Input 4 Input Electrical Output 1 Output Electrical Output 2 Output Electrical Output 3 Output Electrical Output 4 Output Electrical Parameters Main Name and description Default value Units Value range Filename (.s4p) Device.s4p — — Name and description Default value Units Value range Interpolation Linear — Linear, Cubic Touchstone type file containing 4 port s-parameters data. Numerical Determines the interpolation algorithm for the data 969 4 PORT S PARAMETERS Graphs Name and description Default value Units Value range Calculate graphs False — True, False Define whether to calculate graphs or not Simulation Name and description Default value Units Value range Enabled True — True, False False — True, False 64 — [1, 100e6] Determines whether or not the component is enabled Digital filter Determines whether or not the component will use a digital filter to process individual samples Digital filter order The numbers of coefficients for the time domain filter estimation Technical background This component loads a file that describes the small signal scattering matrix, or s parameters, of a device. Data structure of the Touchstone file consists of a header part and a data part (Refer to S Parameters Measured filter for a description of the file format). The content of the file is text data, which is ready to be read with a general text editor. 970 PHASE SHIFT Phase Shift Adds a time phase advance/delay to the optical signal input. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Phase shift 0 deg, rad ]-INF,+INF[ Name and description Default value Units Value range Enabled True — True, False Phase shift to apply to the signal Simulation Determines whether or not the component is enabled 971 PHASE SHIFT Notes: 972 TIME DELAY Time Delay Adds a time delay to the optical signal input. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Units Value range Delay 0 s s, ms, ns [0,+INF[ Name and description Default value Units Value range Enabled True — True, False True — True, False True — True, False Delay to apply to the signal input Simulation Determines whether or not the component is enabled Carrier phase shift Determines whether the carrier phase shift is included in the calculation or not Discrete delay If the parameter Discrete delay is true, the delay is rounded to a multiple of the sampling period, otherwise the time shift property of the Fourier transform is applied using the exact delay value 973 TIME DELAY Notes: 974 OPTICAL ATTENUATOR Optical Attenuator Attenuates the optical signal power. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Default unit Value range Attenuation 0 dB [0,+INF[ Name and description Default value Units Value range Enabled Determines whether or not the component is enabled True — True, False Power attenuation Simulation 975 OPTICAL ATTENUATOR Technical background The signal input electrical field for both polarizations is attenuated as: E OutX ,Y ( t ) = EInX ,Y ( t )10 where α is the power attenuation. 976 –-----α20 (2) ATTENUATOR BIDIRECTIONAL Attenuator Bidirectional This component attenuates the optical signal. It is bidirectional, with wavelength dependent attenuation and return loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Wavelength dependence Independent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] 0 dB [0, +INF] 3 dB [0, +INF] Defines the central wavelength when using wavelength dependent parameters Bandwidth Defines the bandwidth when using wavelength dependent parameters Attenuation Component attenuation at the operating wavelength Max. attenuation Component attenuation outside the operating bandwidth 977 ATTENUATOR BIDIRECTIONAL Name and description Default value Units Value range Return loss 65 dB [0, +INF] 60 dB [0, +INF] Component return loss at the operating wavelength Min. return loss Component return loss outside the operating bandwidth Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Define whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Wavelength lower limit for the graphs To Wavelength upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 978 ATTENUATOR BIDIRECTIONAL Graphs Name and description X Title Y Title Attenuation Wavelength (m) Attenuation Return loss Wavelength (m) Return loss Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 α ( f ) + E In1 RL ( f ) E Out 2 = E In1 α ( f ) + E In2 RL ( f ) (1) where (f) and RL(f) are frequency/wavelength dependent attenuation and return losses respectively: α ( f ) = 10 –α ------20 RL ( f ) = 10 H( f) – RL Min ----------------20 1 – H(f) 2 where a is defined by the parameter Attenuation and α ( f ) has the maximum value defined by the parameter Max. attenuation. RLMin is defined by the parameter Min. return loss, and RL(f) has the maximum value defined by the parameter Return loss. The parameter Wavelength dependence defines the calculation equation for H(f): Wavelength Independent: Wavelength Dependent: 979 ATTENUATOR BIDIRECTIONAL Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of the attenuation and return loss. 980 CONNECTOR Connector This component is an optical connector. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Insertion loss 0 dB [0, +INF] Default unit Units Value range Component insertion loss Simulation Name and description Default value Enabled True [True, False] Determines whether or not the component is enabled Technical Background The signal input electrical field for both polarizations is attenuated as: E Out X, Y = E InX, Y 10 – IL -------20 where IL is the connector Insertion Loss. 981 CONNECTOR Notes: 982 CONNECTOR BIDIRECTIONAL Connector Bidirectional This component is an optical connector. It is bidirectional, with wavelength dependent insertion loss and return loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Wavelength dependence Independent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] 0 dB [0, +INF] 3 dB [0, +INF] Defines the central wavelength when using wavelength dependent parameters Bandwidth Defines the bandwidth when using wavelength dependent parameters Insertion loss Component insertion loss at the operating wavelength Max. insertion loss Component insertion loss outside the operating bandwidth 983 CONNECTOR BIDIRECTIONAL Name and description Default value Units Value range Return loss 65 dB [0, +INF] 60 dB [0, +INF] Component return loss at the operating wavelength Min. return loss Component return loss outside the operating bandwidth Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Wavelength lower limit for the graphs To Wavelength upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 984 CONNECTOR BIDIRECTIONAL Graphs Name and description X Title Y Title Insertion loss Wavelength (m) Insertion loss Return loss Wavelength (m) Return loss Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 IL ( f ) + E In 1 RL ( f ) E Out 2 = E In1 IL ( f ) + E In 2 RL ( f ) (1) where IL(f) and RL(f) are frequency/wavelength dependent insertion and return losses, respectively and are given by: IL ( f ) = 10 – IL -------20 RL ( f ) = 10 H(f) – RL Min ----------------20 1 – H(f) 2 where IL is defined by the parameter Insertion loss and IL(f) has the maximum value defined by the parameter Max. insertion loss. RLMin is defined by the parameter Min. return loss, and RL(f) has the maximum value defined by the parameter Return loss. The parameter Wavelength dependence defines the calculation equation for H(f): Wavelength Independent: Wavelength Dependent: 985 CONNECTOR BIDIRECTIONAL Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of the insertion and return loss. 986 SPATIAL CONNECTOR Spatial Connector This component connects signals with transverse mode profiles. Modes can be translated and rotated, it also propagates the input signals in free-space. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Units Parameters Main Name and description Default value Default unit Value range Insertion loss 0 dB [0, 1e+100] 0 um [0, 1e+100] 0 deg [-1e+100, 1e+100] 0 um [-1e+100, 1e+100] 0 um [-1e+100, 1e+100] 0 deg [-1e+100, 1e+100] Defines the connector insertion loss Distance Defines the free-space distance of propagation Rotation Defines the amount of rotation of the mode profile around the Z-axis X shift Defines the amount of translation of the mode profile in the X-direction Y shift Defines the amount of translation of the mode profile in the Y-direction X tilt Defines the amount of rotation of the mode profile around the X-axis 987 SPATIAL CONNECTOR Name and description Default value Default unit Units Value range Y tilt 0 deg Name and description Default value Default unit Diffraction integral Fast Fourier transform Fast Fourier transform, Direct integration Yes [YES, NO] [-1e+100, 1e+100] Defines the amount of rotation of the mode profile around the Y-axis Numerical Defines the calculation type for the diffraction integral Geometrical loss Units Value range Defines whether the geometrical loss is included in the calculation or not Polarization Name and description Default value Spatial-temporal effect NO Default unit Units Value range [YES, NO] Defines whether the spatial and temporal polarization effects are enabled or not Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NO] Determines whether or not the component is enabled Technical Background The spatial connector allows the user to specify a translational offset and rotation between the two components that should be connected. The parameters X shift and Y shift allow the user to add a transverse offset between the two components. The parameter Distance specifies the free-space propagation distance (the shift in the Zaxis). The free-space propagation is applied using the transfer function of free space in the frequency domain [1][2]. Parameter Diffraction integral defines whether the calculation will use the Fast Fourier Transform or the direct integration of the Rayleigh-Sommerfeld integral [3]. Propagation using the Fast Fourier Transform is limited to tens of microns depending on the size of the spatial mesh, and it is recommended for coupling between devices, such as lasers and fibers. For the same 988 SPATIAL CONNECTOR spatial mesh size, direct integration allows for longer propagation distances; however, it requires more calculation time. Parameter Geometrical loss enables the calculation of the losses if direct integration is selected. The parameter Rotation defines the amount of rotation in the Z-axis, using a twodimensional interpolation technique to rotate the mode profile. The parameters X tilt and Y tilt define the rotation about the X and Y-axis. The tilt in X or Y is applied as a phase delay that is a linear function of the transverse coordinates. The parameter Spatial-temporal effect defines whether the output signal of the connector will store a second signal generated as a result of the coordinate transformation between the two connected components. References [1] J. W. Goodman, Introduction to Fourier Optics, McGraw-Hill, New York, NY 1996. [2] K. Matsushima, H. Schimmel, F.Wyrowski, Fast Calculation Method for Optical Diffraction on Tilted Planes by use of the Angular Spectrum Plane Waves, Optical Society of America, Vol. 20, No. 9, September 2003. [3] N. Delen and B. Hooker, "Free-space beam propagation between arbitrarily oriented planes based on full diffraction theory: a fast Fourier transform approach," J. Opt. Soc. Am. A 15, 857867 (1998) 989 SPATIAL CONNECTOR Notes: 990 REFLECTOR BIDIRECTIONAL Reflector Bidirectional This component is an optical reflector or mirror. It is bidirectional, with wavelength dependent reflection and insertion loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Wavelength dependence Independent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] 99 %, dB [0, 100] 90 %, dB [0, 100] Defines the central wavelength when using wavelength dependent parameters Bandwidth Defines the bandwidth when using wavelength dependent parameters Reflection Component reflection outside the operating bandwidth Min. reflection Component reflection outside the operating wavelength 991 REFLECTOR BIDIRECTIONAL Name and description Default value Units Value range Insertion loss 0 dB [0, +INF] 3 dB [0, +INF] Component insertion loss at the operating wavelength Max. insertion loss Component insertion loss outside the operating bandwidth Graphs Name and description Default value Default Unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graph From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Wavelength lower limit for the graph To Wavelength upper limit for the graph Simulation Name and description Default value Enabled True Units Value range [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins 992 REFLECTOR BIDIRECTIONAL Graphs Name and description X Title Y Title Reflection Wavelength (m) Reflection Transmission Wavelength (m) Transmission Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In2 IL ( f )T ( f ) + E In 1 R ( f ) E Out 2 = E In1 IL ( f )T ( f ) + E In 2 R ( f ) (1) where IS(f), T(f) and R(f) are frequency/wavelength dependent insertion loss, transmission and reflection respectively, and are given by: IL ( f ) = 10 – IL -------20 H(f) T(f) = R 1 – H(f) R(f) = RH ( f ) 2 where IL is defined by the parameter Insertion loss and IL(f) has the maximum value defined by the parameter Max. insertion loss. Where R is defined by the parameter Reflection and R(f) has the minimum value defined by the parameter Min. reflection. The parameter Wavelength dependence defines the calculation equation for H(f) Wavelength Independent: Wavelength Dependent: 993 REFLECTOR BIDIRECTIONAL Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of transmission and reflection. 994 TAP BIDIRECTIONAL Tap Bidirectional This component is a tap. It is bidirectional, with wavelength dependent tap percentage, insertion loss and return loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Parameters Main Name and description Default value Wavelength dependence Dependent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] 5 % [0, 100] Defines the central wavelength when using wavelength dependent parameters Bandwidth Defines the bandwidth when using wavelength dependent parameters Tap percentage Component tap percentage at the operating wavelength 995 TAP BIDIRECTIONAL Name and description Default value Units Value range Min. tap percentage 0 % [0, 100] 0 dB [0, +INF] 3 dB [0, +INF] 65 dB [0, +INF] 60 dB [0, +INF] Component tap percentage outside the operating bandwidth Insertion loss Component insertion loss at the operating wavelength Max. insertion loss Component insertion loss outside the operating bandwidth Return loss Component return loss at the operating wavelength Min. return loss Component return loss outside the operating bandwidth Graphs Name and description Default value Default Unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Defines whether to calculate graphs or not Number of points Number of points for the graph From 1500 nm nm [100, 2000] 1600 nm nm [100, s2000] Wavelength lower limit for the graph To Wavelength upper limit for the graph Simulation Name and description Default value Enabled True Units Value range [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Defines whether to adapt the noise bins or not 996 Default unit Units Value range [True, False] TAP BIDIRECTIONAL Name and description Default value Noise threshold Default unit Units Value range -100 dB [-INF, +INF] 3 dB [-INF, +INF] Name and description X Title Y Title Coupling ratio 1-1 Wavelength (m) Coupling ratio Coupling ratio 1-2 Wavelength (m) Coupling ratio Insertion loss Wavelength (m) Insertion loss Return loss Wavelength (m) Return loss Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = IL ( f ) ( E In2 C 11 ( f ) + EIn3 C 12 ( f ) ) + E In 1 RL ( f ) E Out 2 = IL ( f )EIn1 C 11 ( f ) + E In 2 RL ( f ) E Out 3 = IL ( f )EIn1 C 12 ( f ) + E In 3 RL ( f ) where IL(f) and RL(f) are frequency/wavelength dependent insertion and return losses, respectively. IL ( f ) = 10 –-------IL 20 RL ( f ) = 10 H(f) – RL Min ----------------20 1 – H(f) 2 where IL is defined by the parameter Insertion loss and IL(f) has the maximum value defined by the parameter Max. insertion loss. RLMin is defined by the parameter Min. return loss, and RL(f) has the maximum value defined by the parameter Return loss. 997 TAP BIDIRECTIONAL C11(f) and C12(f) are given by: where r is defined by the parameter Tap percentage and C11(f) and C12(f) have the minimum values defined by the parameter Min. tap percentage. The parameter Wavelength dependence defines the calculation equation for H(f): Wavelength Independent: Wavelength Independent: Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of the coupling ratios, insertion and return loss. 998 LUNA TECHNOLOGIES OVA MEASUREMENT Luna Technologies OVA Measurement This component allows for the loading of measurements of the wavelength dependence of the Jones matrix previously saved by Luna Technologies Optical Vector Analyzer (OVA) software. Ports Name and description Port type Signal type Input Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Filename data.bin — — Start frequency: 195307.401924389 GHz Sample frequency: 0.333433376455307 GHz Start wavelength: 1535 nm End wavelength: 1542 nm File name with the OVA measurements Properties Read-only parameter with the properties of the measurement data File format version: 3 Segment size: 2853 Measurement type: 1 Length of DUT: 6.5 m Number of averages: 0 Pulse Compression parameters = Average dispersion: 0 ps/nm Reference wavelength: 1550 nm Dispersion slope: 0 ps/nm2 Status: 0 Date and time stamp 0/0/0 Device Descriptor NONE 999 LUNA TECHNOLOGIES OVA MEASUREMENT Graphs Name and description Default value Calculate graphs Default Unit Units Value range False — True, False 100 — [10,100e6] Defines whether to calculate graphs or not Number of points Number of points for the graph From 1500 nm nm [100,2000] 1600 nm nm [100,2000] Wavelength lower limit for the graph To Wavelength upper limit for the graph Simulation Name and description Default value Units Value range Enabled True — True, False Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Name and description X Title Y Title Insertion loss Wavelength (m) Insertion loss (dB) Group delay Wavelength (m) Group delay (ps) 1000 LUNA TECHNOLOGIES OVA MEASUREMENT Technical background This component allows for loading measurements of the wavelength dependence of the Jones matrix [1] from a binary file previously saved by the Luna Optical Vector Analyzer [2] user software (versions 3 and 3.2). The Luna OVA is capable of capturing the complete Jones matrix with all the relative phase information. These fundamental elements can then be used in their raw form in OptiSystem for device and system modeling. The Jones matrix describes how the device affects the amplitude, phase and polarization state of the light: J 11 ( ω ) J 12 ( ω ) J(ω) = (1) J 21 ( ω ) J 22 ( ω ) and J kl ( ω ) = m kl ( ω )e iφkl ( ω ) where J kl is a complex number that represents the amplitude ( m ) and phase ( φ ) for each element kl of the matrix. The parameter Filename defines the measurement data. After loading the data the parameter Properties will display the essential information describing the properties of the measurement such as start and sample frequencies, start and end wavelengths, file format version, segment size, measurement type, etc. The user can also verify the filter insertion loss and group delay by enabling the parameter Calculate graphs. If Calculate graphs is enabled, the graphs are available in the Project Browser under the component graphs folder. The insertion loss is calculated in dB according to: 2 2 2 2 ⎛ J 11 + J 12 + J 21 + J 22 ⎞ -⎟ IL = 10 log ⎜ --------------------------------------------------------------------2 ⎝ ⎠ (2) The group delay in seconds is calculated according to: ∠( J 11n + 1 J 11n∗ + J 12n + 1 J 12n∗ + J 21n + 1 J 21n∗ + J 22n + 1 J 22n∗ ) GD = ---------------------------------------------------------------------------------------------------------------------------------------------------Δω where Δω is the optical frequency increment between points. 1001 (3) LUNA TECHNOLOGIES OVA MEASUREMENT References: [1] D. S. Klieger, J. W. Lewis, C.E. Randall, Polarized Light in Optical and Spectroscopy, Academic Press, 1990. [2] http://www.lunatechnologies.com/products/ 1002 MEASURED COMPONENT Measured Component This component allows for loading measurements of the wavelength dependence of the Jones matrix. It provides a transfer function that describes the amplitude, phase, and polarization state of 1xN devices. Ports Name and description Port type Signal type Input Input Optical Output1 Output Optical Output2 Output Optical Parameters Main Name and description Default value Units Value range Filename measurement.txt — — File name with the Jones matrix measurement Graphs Name and description Default value Calculate graphs Default Unit Units Value range False — True, False 100 — [10,100e6] nm [100,2000] Defines whether to calculate graphs or not Number of points Number of points for the graph From 1500 nm Wavelength lower limit for the graph 1003 MEASURED COMPONENT Name and description Default value Default Unit Units Value range To 1600 nm nm [100,2000] Wavelength upper limit for the graph Simulation Name and description Default value Units Value range Enabled True — True, False Name and description Default value Units Value range Noise threshold –100 dB ]-INF,+INF[ 3 dB ]-INF,+INF[ Determines whether or not the component is enabled Noise Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Name and description X Title Y Title Transmission Wavelength (m) Transmission (dB) Group delay Wavelength (m) Group delay (ps) Technical background This component allows for loading measurements of the wavelength dependence of the Jones matrix [1] from a text file. This text file can be generated by measurement equipment such as the Agilent 81910A Photonic All-Parameter Analyzer [2], Fiberwork OSPA (Optical Parameter Analyzer [3]), or directly by the user. The Jones matrix describes how the device affects the amplitude, phase and polarization state of the light: J(ω) = 1004 J 11 ( ω ) J 12 ( ω ) J 21 ( ω ) J 22 ( ω ) (1) MEASURED COMPONENT and J kl ( ω ) = m kl ( ω )e iφkl ( ω ) where J kl is a complex number that represents the amplitude ( m ) and phase ( φ ) for each element kl of the matrix. The 81910A has only one output and one input, so it can only measure one channel at a time. However there is the ability to combine multiple measurements (channels) into one file. The Measured Component can load files with multiple measurement, and for every channel it will generate one port. N measurements will generate N output ports. The first three rows of the file are used for the header or comments. Comments are delimited by the character '%', for example: %Agilent Technologies Photonic Foundation Library 2.60.09 (2)… %Wavelength,Amp(j11),Phase(j11),Amp(j12),Phase(j12),Amp(j21),P hase(j21),Amp(j22),… %Channel_1 Tx, MeasurementChannel_1 Rx, Measurement… Each measurement has 9 columns, the wavelength in meters, the magnitude (amplitude) and phase (radians) of the 4 Jones terms: Wavelength,Amp(J11),Arg(J11),Amp(J12),Arg(J12),Amp(J21),Arg(J21),Amp(J22),Ar g(J22)… For example: 1.541e6,0.0072341,2.9,0.0041225,2.9,0.0052406,2.9,0.0073904,2. 9… 1.542e6,0.0072341,2.9,0.0041225,2.9,0.0052406,2.9,0.0073904,2. 9… Multiple measurements can be combined in the same file, for example, when measuring the transmission and reflection of one component, the file will have 18 columns, 9 values for each measurement (Tx and Rx). The user can also verify the filter insertion loss and group delay by enabling the parameter Calculate graphs. If Calculate graphs is enabled, the graphs are available in the Project Browser under the component graphs folder. 1005 MEASURED COMPONENT The insertion loss is calculated in dB according to: 2 2 2 2 ⎛ J 11 + J 12 + J 21 + J 22 ⎞ IL = 10 log ⎜ ---------------------------------------------------------------------⎟ 2 ⎝ ⎠ (2) The group delay in seconds is calculated according to: ∠( J 11n + 1 J 11n∗ + J 12n + 1 J 12n∗ + J 21n + 1 J 21n∗ + J 22n + 1 J 22n∗ ) GD = ---------------------------------------------------------------------------------------------------------------------------------------------------Δω where (3) Δω is the optical frequency increment between points. References: [1] D. S. Klieger, J. W. Lewis, C.E. Randall, Polarized Light in Optical and Spectroscopy, Academic Press, 1990. [2] http://www.agilent.com/ [3] http://www.fiberwork.com.br/ 1006 SPATIAL APERTURE Spatial Aperture This component applies a circular or square window to the transverse mode profiles. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Main Name and description Default value Aperture type Circular Value range [Circular, Square] Defines the aperture type Width 10 um Name and description Default value Default unit Enabled YES [0, 1e+100] Defines the width of the square aperture or the diameter of the circular aperture Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Technical Background The spatial aperture component truncates the incident optical field. The component also attenuates the time-domain waveform of the signal. The attenuation is the power lost in the aperture. 1007 SPATIAL APERTURE Notes: 1008 THIN LENS Thin Lens This component applies a phase transformation to the transverse mode profiles, affecting the focus of the signal beam. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Units Parameters Main Name and description Default value Default unit Focal length 10 mm Defines the focal length Aperture effects NO Value range [1-e+100, 1e+100] [YES, NO] Defines whether the lens will cause aperture effects or not Lens diameter 5 mm [0, 1e+100] 0 % [0, 100] 100 % [0, 100] Defines the width of the of the circular aperture Lens reflectance Defines the lens reflectance Outer reflectance Defines the reflectance outside of the lens diameter 1009 THIN LENS Simulation Name and description Default value Enabled YES Default unit Units Value range [YES, NO] Determines whether or not the component is enabled Technical Background This component is an optical lens modeled using the thin lens approximation [1]. The applied phase transformation is given by: 2 2 π( x + y ) T ( x, y ) = exp – j ------------------------- (1) λf where f is the focal length. Additionally, aperture effects can be modeled using the parameter Lens diameter and the reflectance inside and outside of the lens. References [1] J. W. Goodman, “Introduction to Fourier Optics”, McGraw-Hill, New York, NY 1996. 1010 VORTEX LENS Vortex Lens This component is a combination of a parabolic lens and a phase vortex. Similar to the thin lens component, it applies a phase transformation to the transverse mode profiles, affecting the focus of the signal beam. Ports Name and description Port type Signal type Supported Modes Input Input Optical Sample signals Output Output Optical Default unit Units Parameters Main Name and description Default value Vortex parameter 2 [1-e+100, 1e+100] 1 [1-e+100, 1e+100] Defines the lens vortex parameter m Refractive index Defines the lens refractive index n Focal length 10 mm Defines the focal length Aperture effects NO Value range [1-e+100, 1e+100] [YES, NO] Defines whether the lens will cause aperture effects or not Lens diameter 5 mm [0, 1e+100] 0 % [0, 100] Defines the width of the of the circular aperture Lens reflectance Defines the lens reflectance 1011 VORTEX LENS Name and description Default value Default unit Outer reflectance 100 % Name and description Default value Default unit Enabled YES Units Value range [0, 100] Defines the reflectance outside of the lens diameter Simulation Units Value range [YES, NO] Determines whether or not the component is enabled Technical Background This component is an optical lens modeled using the thin lens approximation [1]. The applied phase transformation is given by: 2 2 πn ( x + y ) T ( x, y ) = exp – j ---------------------------- + m atan ⎛⎝ x--⎞⎠ 2λf y (1) Where f is the focal length, m is the vortex parameter and n is the refractive index. Additionally, aperture effects can be modeled using the parameter Lens diameter and the reflectance inside and outside of the lens. References [1] E. G. Johnson, J. Stack, C. Koehler, "Light Coupling by a Vortex Lens into Graded Index Fiber", Journal of Lightwave Technology, VOL. 19, NO. 5, May 2001. 1012 X COUPLER X Coupler Cross coupler for combining or splitting optical signals. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Units Value range Coupling coefficient 0.5 — [0,1] 0 dB [0,+INF[ True — True, False Coupling factor from port 1 to port 2 Additional loss Loss applied to the signal after coupling Conjugate Defines whether the component uses the complex conjugate definition or not 1013 X COUPLER Technical background The transmission matrix for the cross: ⎛ E 1OutX ,Y⎞ ⎛ 1–c ⎜ ⎟ = α⎜ ⎝ E 2OutX ,Y⎠ ⎝ pj c pj c⎞ ⎛ E 1InX ,Y⎞ ⎟⎜ ⎟ 1 – c⎠ ⎝ E 2InX ,Y⎠ (1) where p is the signal of the c is coupling coefficient and α is the additional loss. If the parameter Conjugate is disabled, p is positive (value = 1), and the coupler will use the definition of [1], otherwise p is negative (value = -1) and the coupler will use the definition of [2]. References [1] Gerd Keiser, “Optical Fiber Communications,” Third Edition, McGraw-Hill, Higher Education, 2000. [2] Christi K. Madsen and Jian H. Zhao, "Optical Filter Design and Analysis, A Signal Processing Approach", (John Wiley & Sons, New York, 1999). 1014 PUMP COUPLER CO-PROPAGATING Pump Coupler Co-Propagating Equivalent to a pump coupler subsystem where you can control the attenuation of the signal and pump independently. Ports Name and description Port type Signal type Signal Input Input Optical Pump Input Input Optical Output Output Optical Parameters Main Name and description Default value Units Value range Signal attenuation 0 dB [0,+INF[ 0 dB [0,+INF[ Signal power attenuation Pump attenuation Pump power attenuation 1015 PUMP COUPLER CO-PROPAGATING Technical background The input signals are attenuated and combined. The subsystem is illustrated in Figure 1. Figure 1 Pump coupler co-propagating subsystem 1016 PUMP COUPLER COUNTER-PROPAGATING Pump Coupler Counter-Propagating Equivalent to a subsystem where you can control the attenuation of the signal and pump independently. Ports Name and description Port type Signal type Signal Input Input Optical Pump Input Input Optical Pump Output Output Optical Output Output Optical Parameters Main Name and description Default value Units Value range Signal attenuation 0 dB [0,+INF[ 0 dB [0,+INF[ Signal power attenuation Pump attenuation Pump power attenuation 1017 PUMP COUPLER COUNTER-PROPAGATING Technical background The input signals are attenuated independently. The subsystem is illustrated in Figure 1. Figure 1 Pump coupler counter-propagating subsystem 1018 COUPLER BIDIRECTIONAL Coupler Bidirectional This component is a cross-coupler for combining or splitting the optical signal. It is bidirectional, with wavelength dependent coupling, insertion loss and return loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Input 4 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Parameters Main Name and description Default value Wavelength dependence Independent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] Defines the central wavelength when using wavelength dependent parameters Bandwidth Defines the bandwidth when using wavelength dependent parameters 1019 COUPLER BIDIRECTIONAL Name and description Default value Units Value range Coupling ratio 50 % [0, 100] 0 % [0, 100] 0 dB [0, +INF] 3 dB [0, +INF] 65 dB [0, +INF] 60 dB [0, +INF] True — True, False Coupling ratio at the operating wavelength Min. coupling ratio Component coupling ratio at the operating wavelength Insertion loss Component insertion loss at the operating wavelength Max. insertion loss Component insertion loss outside the operating bandwidth Return loss Component return loss at the operating wavelength Min. return loss Component return loss outside the operating bandwidth Conjugate Defines whether the component uses the complex conjugate definition or not Graphs Name and description Default value Default unit Units Value range Calculate graphs False [True, False] 100 [10, 100e6] Define whether to calculate graphs or not Number of points Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Wavelength lower limit for the graphs To Wavelength upper limit for the graphs Simulation Determines whether or not the component is enabled 1020 [True, False] COUPLER BIDIRECTIONAL Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Name and description X Title Y Title Coupling ratio 1-1 Wavelength (m) Coupling ratio Coupling ratio 1-2 Wavelength (m) Coupling ratio Insertion loss Wavelength (m) Insertion loss Return loss Wavelength (m) Return loss Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = IL ( f ) ( E In3 C 11 ( f ) + jE In4 C 12 ( f ) ) + E In1 RL ( f ) E Out 2 = IL ( f ) ( jE In3 C 12 ( f ) + E In4 C 11 ( f ) ) + E In2 RL ( f ) E Out 3 = IL ( f ) ( E In1 C 11 ( f ) + jE In2 C 12 ( f ) ) + E In3 RL ( f ) E Out 4 = IL ( f ) ( jE In1 C 12 ( f ) + E In2 C 11 ( f ) ) + E In4 RL ( f ) where IL(f) and RL(f) are frequency/wavelength dependent insertion and return losses, respectively. IL ( f ) = 10 –-------IL 20 RL ( f ) = 10 H(f) – RL Min ----------------20 1 – H(f) 2 where IL is defined by the parameter Insertion loss and IL(f) has the maximum value defined by the parameter Max. insertion loss. RLMin is defined by the parameter Min. return loss, and RL(f) has the maximum value defined by the parameter Return loss. 1021 COUPLER BIDIRECTIONAL C11(f) and C12(f) are given by: where r is defined by the parameter Coupling ratio and C11(f) and C12(f) have the minimum values defined by the parameter Min. coupling ratio. The parameter Wavelength dependence defines the calculation equation for H(f): Wavelength Independent: Wavelength Dependent: Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of the coupling ratios, insertion and return loss. Refer to the X Coupler component for the description of parameter Conjugate. 1022 PUMP COUPLER BIDIRECTIONAL Pump Coupler Bidirectional This component is a pump-coupler for combining signals and pumps. It is bidirectional, with wavelength dependent isolation, insertion loss and return loss. Ports Name and description Port type Signal type Input 1 Input Optical Input 2 Input Optical Input 3 Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Parameters Signal Input/Output Name and description Default value Signal wavelength dependence Dependent Units [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Signal operating wavelength Value range 1550 Hz, THz, nm [100, 2000] 130 Hz, GHz, THz, nm [0, 200] 0 dB [0, +INF] Defines the central wavelength when using wavelength dependent parameters Signal operating bandwidth Defines the bandwidth when using wavelength dependent parameters Signal insertion loss Component isolation at the operating wavelength 1023 PUMP COUPLER BIDIRECTIONAL Name and description Default value Units Value range Signal return loss 65 dB [0, +INF] 60 dB [0, +INF] 55 dB [0, +INF] Name and description Default value Units Value range Pump wavelength dependence Dependent Component return loss at the operating wavelength Min. signal return loss Component insertion loss outside the operating bandwidth Signal isolation Component isolation at the operating wavelength Pump Input/Output [Independent, Dependent, Cosine] Defines the type of wavelength dependence for component parameters Pump operating wavelength 980 Hz, THz, nm [100, 2000] 50 Hz, GHz, THz, nm [0, 200] 0 dB [0, +INF] 65 dB [0, +INF] 60 dB [0, +INF] 55 dB [0, +INF] Default unit Units Value range Defines the central wavelength when using wavelength dependent parameters Pump operating bandwidth Defines the bandwidth when using wavelength dependent parameters Pump insertion loss Component insertion loss at the operating wavelength Pump return loss Component return loss at the operating wavelength Min. pump return loss Component insertion loss outside the operating bandwidth Pump isolation Component return loss at the operating wavelength Graphs Name and description Default value Calculate graphs False Define whether to calculate graphs or not 1024 [True, False] PUMP COUPLER BIDIRECTIONAL Name and description Default value Number of points 100 Default unit Units Value range [10, 100e6] Number of points for the graphs From 1500 nm nm [100, 2000] 1600 nm nm [100, 2000] Name and description Default value Default unit Units Value range Enabled True Wavelength lower limit for the graphs To Wavelength upper limit for the graphs Simulation [True, False] Determines whether or not the component is enabled Noise Name and description Default value Adaptive noise bins True Default unit Units Value range [True, False] Define whether to adapt the noise bins or not Noise threshold -100 dB [-INF, +INF] 3 dB [-INF, +INF] Minimum value for adaptation of noise bins Noise dynamic Threshold ratio for adaptation of noise bins Graphs Name and description X Title Y Title Pump input/output insertion loss Wavelength (m) Insertion loss Pump input/output return loss Wavelength (m) Return loss Signal input/output insertion loss Wavelength (m) Insertion loss Signal input/output return loss Wavelength (m) Return loss 1025 PUMP COUPLER BIDIRECTIONAL Technical Background The signal input electrical field for both polarizations for each output port is calculated according to: E Out 1 = E In3 IL S ( f ) + E In1 RL S ( f ) E Out 2 = E In3 IL P ( f ) + E In 2 RL P ( f ) E Out 3 = E In1 IL S ( f ) + E In2 IL P ( f ) + E In3 ILs ( f ) + E In3 RL P ( f ) where ILS(f)/ILP(f) and RLS(f)/RLP(f) are frequency/wavelength dependent insertion and return losses for signals and pumps. IL S ( f ) = 10 – ILS ----------20 RL S ( f ) = 10 H(f) – RL S Min -------------------20 1 – H(f) 2 where ILS is defined by the parameter Signal insertion loss and ILS(f) has the maximum value defined by the parameter Signal isolation. RLSMin is defined by the parameter Min. signal return loss, and RLS(f) has the maximum value defined by the parameter Signal return loss. IL P ( f ) = 10 – IL P ----------20 RL P ( f ) = 10 H( f) – RLP Min -------------------20 1 – H(f) 2 where ILP is defined by the parameter Pump insertion loss and ILP(f) has the maximum value defined by the parameter Pump isolation. RLPMin is defined by the parameter Min. pump return loss, and RLP(f) has the maximum value defined by the parameter Pump return loss. The parameter Wavelength dependence defines the calculation equation for H(f): Wavelength Independent: Wavelength Dependent: 1026 PUMP COUPLER BIDIRECTIONAL Cosine Dependent: where If the parameter Calculate graphs is enabled, the component will generate graphs with the wavelength dependence of the insertion and return losses for the signal and pump ranges. 1027 PUMP COUPLER BIDIRECTIONAL Notes: 1028 POWER SPLITTER 1X2 Power Splitter 1x2 Ideal power splitter — splits an optical input signal into two output signals. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,+INF[ Loss applied to the signal after splitting 1029 POWER SPLITTER 1X2 Technical background The signal output for each port is attenuated by: –-----α20 EInX ,Y ( t )10 E OutX ,Y ( t ) = -----------------------------N where α is the power attenuation and N is the number of output ports (N=2). 1030 (1) POWER SPLITTER 1X4 Power Splitter 1x4 Ideal power splitter — splits an optical input signal in four output signals. Ports Name and description Port type Signal type Input Input Optical Output 1 Output Optical Output 2 Output Optical Output 3 Output Optical Output 4 Output Optical Parameters Main Name and description Default value Units Value range Loss 0 dB [0,+INF[ Loss applied to the signal after splitting 1031 POWER SPLITTER 1X4 Technical background The signal output for each port is att