Rangkaian Jembatan Arus Bolakbalik ver1

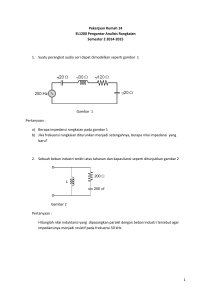
JEMBATAN ARUS BOLAK – BALIK
Nama
NRP
Kelas
Simon Patabang, MT.
:Muhammad Ali Maskur
:1303191002
:1 D3 Teknik Elektro Industri A
Rangkaian Jembatan Arus AC
Bentuk umum dari jembatan arus bolak balik yang
terdiri dari :
• Empat lengan yaitu Z1, Z2, Z3, dan Z4, merupakan
impedansi yang nilainya tidak ditetapkan.
• Sebuah detektor nol yang berfungsi memberi
respons terhadap ketidaksetimbangan arus bolak
balik.
Syarat kesetimbangan pada
jembatan arus bolak balik (sama
seperti jembatan arus searah),
diperoleh jika :
1. Respons detektor adalah nol
2. Mengubah salah satu atau lebih dari lengan
(impedansi) jembatan hingga mendapatkan
respons detektor menjadi nol.
• Persamaan umum untuk kesetimbangan jembatan
dinyatakan dengan notasi kompleks, dimana
besaran-besaran bisa berupa impedansi dan
admitansi.
• Untuk mendapatkan kesetimbangan jembatan, maka
beda potensial dari titik A ke titik C sama dengan nol
( VAC = 0 ), dan kondisi ini akan dicapai bila drop
tegangan dari B ke A sama dengan drop tegangan
dari B ke C ( VBA = VBC ).
• Dalam notasi kompleks didefinisikan sebagai berikut :
E BA  E BC atau I1Z1  I 2 Z 2 …..(1)
Jika arus detektor nol, maka :
E
I1 
Z1  Z 3
E
…..(2) dan I 2 
Z2  Z4
Subsitusikan I1 dan I2 :
I1Z1  I 2 Z 2
Z1
Z2

Z1  Z 3 Z 2  Z 4
Z1Z 2  Z1Z 4  Z1Z 2  Z 2 Z 3
…..(3)
Z1 Z 4  Z 2 Z 3
…..(4)
Bentuk persamaan dengan menggunakan admitansi :
Y1Y4  Y2Y3
…..(5)
Persamaan (5) umumnya digunakan jika komponenkomponen pada lengan jembatan terhubung paralel.
Jika
impedansi
dituliskan
Z | Z | 
dimana:
Z = magnitudo dan
θ = sudut fasa
dalam
bentuk
:
• Persamaan (4) dapat ditulis :
Z1 Z 4  Z 2 Z 3
Z11.Z 4  4  Z 2  2 .Z 3 3
Z1.Z 4 ( 4  1 )  Z 2 .Z 3 ( 3   2 )
…..(6)
• Persyaratan yang harus dipenuhi untuk membuat
jembatan arus bolak balik setimbang, yaitu :
1. Kesetimbangan magnitudo impedansi memenuhi
hubungan : Z1Z 4  Z 2 Z 3
2. Sudut-sudut
fasa
impedansi
memenuhi
hubungan       
1
4
2
3
Contoh :
1. Impedansi-impedansi jembatan arus
bolak balik adalah :
Z1 = 100/80° Ω ( impedansi induktif )
Z2 = 250 Ω ( tahanan murni )
Z3 = 400 /30° Ω ( impedansi induktif )
Z4 = tidak diketahui ( dicari )
Tentukan nilai Z4
Penyelesaian :
Syarat pertama untuk kesetimbangan adalah :
Z 2Z3
Z4 
Z1
Z1 Z 4  Z 2 Z 3
250.400
Z4 
 1000
100
• Syarat kedua untuk kesetimbangan jembatan
adalah :       
1
4
2
3
 4   2   3  1
 4  0  30   80   50 
Jadi nilai Z4 dalam bentuk polar :
Z 4  1000   50 
2. Jika Jembatan arus bolak balik seperti di atas dalam
keadaan setimbang dengan impedansi sebagai berikut :
Z1 terdiri dari R = 450 Ω ; Z2 terdiri dari R = 300 Ω , seri
dengan C = 0,265 μF ; Z4 tidak diketahui ; Z3 terdiri dari R
= 200 Ω seri dengan L = 15,9 mH, jika frekuensi osilator 1
KHz, tentukan impedansi pada lengan CD.
Penyelesaian :
Impedansi lengan-lengan jembatan
dalam bentuk kompleks adalah :
Z1 = R
Z2 = R - j XC
Z3 = R + jXL
Z4 = ?
dinyatakan
Xc = 1/ ωC
Xc = 1/ (2πfC) = 1/(2π.1000. 0,265 10⁻⁶)
Xc = 600 Ω
XL = ωL
XL = 2πfL = 2πf.1000. 15,9 .10⁻³ = 100 Ω
Maka :
Z1 = 450 Ω
Z2 = 300 + j600 Ω
Z3 = 200 + j100 Ω
Z 2Z3
Z4 
Z1
(300  j 600)(200  j100)
Z4 
450
60.000  j30.000  j120.000  60.000)
Z4 
450
120.00  j90.000)
Z4 
 266,6 - j 200 
450
Impedansi Z4 merupakan gabungan sebuah tahanan
resistor 266,6 Ω dan reaktansi kapasitif Xc 200 Ω yang
dihubungkan seri ( Z4 = R - j Xc )
1
1
XC 

C 2fC
1
200 
2 1.000.C

C  0,8F
Jembatan Pembanding Kapasitansi
Jembatan pembanding kapasitansi digunakan untuk
pengukuran kapasitansi yang tidak diketahui, dengan
cara
membandingkannya
terhadap
sebuah
kapasitansi yang diketahui.
• Kedua lengan pembanding
adalah resistif, yaitu : tahanan
variabel R1 dan tahanan R2.
• Lengan standar terdiri dari :
tahanan variabel Rs dihubung
seri dengan kapasitor standar
kualitas tinggi Cs.
• Cx adalah kapasitansi yang
tidak diketahui.
• Rx adalah tahanan bocor
kapasitor.
• Impedansi dinyatakan dalam bentuk bilangan
kompleks, yaitu :
• Subsitusi nilai impedansi ke persamaan (4) :
• Dengan menyamakan bagian-bagian nyata
• Dengan menyamakan bagian-bagian khayal
• Agar memenuhi kedua syarat setimbang dalam
konfigurasinya, jembatan harus mengandung dua elemen
variabel R1 dan Rs.
Jembatan Pembanding Induktansi
• Jembatan pembanding induktansi mirip dengan jembatan
pembanding kapasitansi.
• Induktansi yang tidak diketahui ditentukan dengan
membandingkan terhadap sebuah induktor standar yang
diketahui seperti yang diunjukkan pada diagram gambar.
• Impedansi dalam bentuk bilangan kompleks, yaitu :
• Subsitusi nilai impedansi ke persamaan (4) :
• Dengan menyamakan bagian-bagian nyata :
• Dengan menyamakan bagian-bagian nyata
• Dalam jembatan ini, R2 dipilih sebagai pengontrol
kesetimbangan induktif, dan Rs adalah pengontrol
keseimbangan resistif.
1. Jembatan Maxwell
• Jembatan Maxwell, digunakan untuk mengukur sebuah
induktansi yang tidak diketahui, yang dinyatakan dalam
kapasitansi yang diketahui.
• Pada gambar, ditunjukkan rangkaian jembatan Maxwell,
dimana salah satu lengan pembanding mempunyai
sebuah tahanan yang dihubung paralel dengan sebuah
kapasitansi.
Impedansi ketiga lengan dan admitansi lengan 1,
dinyatakan dalam bentuk bilangan kompleks :
Persamaan umum kesetim
bangan jembatan, menyata
kan :
Subsitusikan harga-harga Z2, Z3, Y1, dan ZX
kedalam persamaan (4)
• Dengan menyamakan bagian-bagian nyata :
• Dengan menyamakan bagian-bagian nyata
• Karena jumlah sudut fasa dari elemen resistif pada
lengan 2 dan 3 sama dengan nol, maka jumlah sudut fasa
pada lengan 1 dan 4 harus sama dengan nol ( syarat
kedua kesetimbangan ).
• Untuk menyetimbangkan jembatan Maxwell,
pertama-tama yang dilakukan adalah mengatur
tahanan R3 untuk kesetimbangan induktif dan
kemudian mengatur R1 untuk kesetimbangan resistif.
2. Jembatan Hay
• Jembatan hay, digunakan untuk mengukur
sebuah induktansi yang tidak diketahui, yang
dinyatakan dalam kapasitansi yang diketahui.
• Pada gambar, ditunjukkan rangkaian jembatan
Hay yang berbeda dari jembatan Maxwell,
dimana tahanan R1 dihubungkan seri dengan
kapasitor C1.
• Impedansi keempat lengan dinyatakan dalam bentuk
bilangan kompleks :
• Subsitusikan harga-harga Z1, Z2, Z3,dan Z4 ke dalam
persamaan kesetimbangan (4)
• Dengan menyamakan sisi real dan khayal maka
diperoleh :
dan
• Pada persamaan ( Rx) dan ( Lx ), dapat dilihat bahwa harga
tahanan dan induktansi yang tidak diketahui ( Rx dan Lx )
mengandung kecepatan sudut ω, yang berarti bahwa frekuensi
harus diketahui secara tepat.
• Syarat kedua kesetimbangan, menyatakan bahwa jumlah
sudut fasa dari lengan-lengan berhadapan harus sama,
jadi jumlah sudut fasa induktif harus sama dengan jumlah
sudut fasa kapasitif, karena sudut-sudut fasa resistif
adalah nol.
• Pada gambar berikut, ditunjukkan diagram vektor bahwa :
• tangen sudut fasa induktif adalah :
• tangen sudut fasa kapasitif adalah :
• Jika kedua sudut fasa tersebut sama, maka besar
tangennya juga sama, jadi :
• Subsitusikan harga pada persamaan di tas ke dalam
persamaan Lx), maka bentuk Lx menjadi :
Untuk nilai Q lebih besar dari 10 ( Q > 10 ), maka suku
(1/Q)² menjadi lebih kecil dar 1/100, sehingga dapat
diabaikan, oleh karena itu persamaan berubah menjadi
bentuk yang sama ( diturunkan ) pada jembatan Maxwell,
yaitu :
3. Jembatan Schering
• Jembatan arus bolak balik yang paling penting dan
digunakan secara luas untuk pengukuran kapasitor, dan
mengukur sifat-sifat isolasi, yaitu pada sudut-sudut fasa
yang mendekati 90°.
• Jembatan ini memberikan beberapa keuntungan nyata
dibandingkan dengan jembatan pembanding kapasitansi.
• Pada lengan 1 terdiri dari tahanan R1 diparalel dengan
sebuah kapasitor variabel dan lengan standar hanya
terdiri dari sebuah kapasitor ( umumnya kapasitor
standar merupakan kapasitor mika yang bermutu tinggi
untuk pengukuran yang umum dan kapasitor udara untuk
pengukuran isolasi ).
• Sebuah kapasitor mika bermutu tinggi mempunyai
kerugian yang sangat rendah ( tidak mempunyai tahanan
bocor), oleh karena itu mempunyai sudut fasa mendekati
90°.
• Impedansi keempat lengan dinyatakan dalam bentuk
bilangan kompleks :
Persamaan umum kesetimbangan jembatan :
• Dengan menyamakan bagian nyata dan bagian khayal,
diperoleh
• Faktor daya untuk besaran yang tidak diketahui adalah
tg θ = Rx/Zx.
• Untuk sudut-sudut fasa yang mendekati 90°, reaktansi
hampir sama dengan impedansi maka faktor daya
didefinisikan :
dimana :
Xx adalah reaktansi kapasitip yg tidak diketahui
Kondisi Tidak Seimbang
• Jika salah satu persyaratan kesetimbangan tidak
dipenuhi, maka sebuah jembatan arus bolak balik sama
sekali tidak dapat disetimbangkan.
• Gambar berikut menggambarkan keadaan ini, dimana Z1
merupakan elemen induktif, Z2 adalah sebuah kapasitif
murni, Z3 adalah sebuah tahanan variabel.
Tahanan R3 diperlukan untuk
menghasilkan kesetimbangan
jembatan, yang ditentukan
dengan menggunakan syarat
kesetimbangan pertama yaitu :
• Syarat kesetimbangan kedua ( sudut-sudut fasa ), yaitu :
Jadi :
yang berarti persyaratan kedua tidak dipenuhi,
sehingga kesetimbangan jembatan tidak dapat
dicapai.
Cara menyetimbangkan sebuah jembatan dimana
pengaturan kecil pada satu atau lebih lengan-lengan
jembatan akan menghasilkan suatu kondisi, dimana
kesetimbangan dapat dicapai.
Contoh :
Rangkaian jembatan seperti pada
gambar, tentukan apakah jembatan
tersebut setimbang sempurna atau
tidak. Jika tidak, tunjukkan dua cara
agar jembatan agar jembatan dapat
menjadi setimbang, dan tentukan
nilai-nilai numerik untuk setiap komponen tambahan.
Anggap bahwa lengan jembatan 4 tidak diketahui dan
tidak dapat diubah.
Penyelesaian :
• Pemeriksaan rangkaian menunjukkan bahwa syarat
pertama kesetimbangan ( kebe-saran ), dengan mudah
dapat dipenuhi, dengan sedikit memperbesar R3.
• Syarat kesetimbangan kedua menetapkan :
jadi, kesetimbangan tidak mungkin dicapai dengan
konfigurasi rangkaian jembatan pada gambar di atas,
karena θ1 + θ4 sedikit negatip, dan θ2 + θ3 = 0°.
• Kesetimbangan jembatan dapat kembali dicapai, dengan
mengubah rangkaian sedemikian rupa, sehingga
persyaratan sudut fasa dipenuhi.
• Ada dua cara untuk melakukan hal tersebut, yaitu :
1. Mengubah Z1
2. Mengubah sudut fasa lengan 2 dan lengan 3
Cara Pertama : Mengubah Z1
• Mengubah Z1, sehingga sudut fasanya berkurang
menjadi lebih kecil dari 90° ( sama dengan θ4 ) , yaitu
dengan menghubungkan sebuah tahanan yang
dihubungkan paralel dengan kapasitor.
• Tahanan R1 dapat ditentukan
dengan menggunakan admitansi
pada lengan satu, maka syarat
kesetimbangan pertama menetapkan :
• Dua bilangan kompleks dikatakan sama, jika bagian riel
dan bagian khayalnya sama, maka :
Perlu diperhatikan bahwa dengan penambahan R1, syarat
kesetimbangan pertama terganggu (Z1 bertambah),
sehingga tahanan variabel R3 harus diatur untuk
mengimbangi pengaruh ini.
Cara kedua : Mengubah sudut fasa lengan 2 dan 3
• Mengubah sudut fasa lengan 2 dan lengan 3, yaitu dengan
menambah sebuah kapasitor yang dihubung seri dengan R3,
seperti ditunjukkan pada gambar berikut :
Dengan menggunakan syarat kesetimbangan pertama,
diperoleh :
dimana :
Subsitusikan harga-harga Z1, Z2, Z3, dan Z4 ke dalam
ketimbangan diperoleh :
Besarnya Z3 telah bertambah, sehingga syarat kesetimbangan
pertama berubah, oleh karena itu suatu pengaturan kecil pada
R3 perlu dilakukan kembali untuk memulihkan kesetimbangan.
Sekian