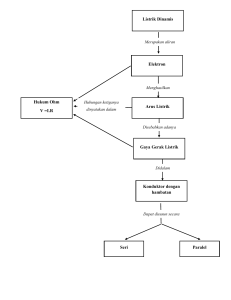
5.1 Elektron Bebas Klasik Kapasitas panas pada suhu tinggi atau suhu ruang menurut Dulong-Petit, Einstein maupun oleh Debye besarnya adalah Cv = 3R. pendapat yang digunakan untuk mendapatkan persamaan tersebut adalah bahwa getaran kisi dalam suatu kristal memiliki energi termal tertentu. Paket getaran energinya dari getaran kisi yang terkuantisasi disebut fonon. Tetapi nilai kapasitas panas atau Cv yang dijabarkan oleh Dulong-Petit, Einstein dan Debye ini belum memasukkan nilai energi termalnya yang tersimpan dalam gerak termal elektron bebas. Jadi, yang dimaksud adalah Cv ini hanya memperhitungkan kehadiran fonon saja sehingga kapasitas panas logam yang hanya memperhitungkan kehadiran elektron dan fonon dapat ditulis sebgai Cv = Cv_fonon + Cv_elektron Cv yang berasal dari kontribusi fonon pada suhu tinggi ini adalah Cv_fonon = 3R. Sedangkan Cv yang berasal dari kontribusi elektron dapat diuraikan dari energi rata-rata elektron pada suhu T dengan jumlah elektron valensi yang disumbangkan oleh satu atom pada kristal yang dilambangkan oleh Zv dengan persamaan berikut. E Zv 3 3 N A k B T Z v RT 2 2 C v _ elektron dE 3 Zv R dT 2 Sehingga Cv yang berasal dari kontribusi fonon dan elektron adalah C v C v _ fonon C v _ elektron 3R 3 3 RZ v 3 Z v R 2 2 Dari nilai penjabarandiatas menunjukkan bahwa kapasitas panas pada suatu kristal yang memiliki elektron bebas (logam) 50% lebih tinggi dari kristal yang tidak memilki elektronbebas (isolator). Pada kenyataannya, pada suhu tinggi atau suhu ruang, kapasitas panas suatu logam tidaklah berharga 1½ kali dari nilai kapasitas panas bahan isolator tetapi hampir sama berharga dengan 3R. Hal ini menunjukkan bahwa kajian kapasitas panas klasik tersebut belum tepat menggambarkan kontribusi dari eleketron bebas terhadap kapasitas panas pada suatu logam. 5.2 Elektron Terkuantisasi Pada fenomena fisika terkhusus konsep kapasitas panas yang dikaitkan dengan keberadaan elektron bebas dalam kristal, ternyata konsep fisika kuantum sangat diperlukan untuk menjelaskan secara jelas. ada dua konsep kuantum pada pembahasan elektron bebas suatu kristal atau zat padat yaitu konsep kuantisasi energi eleketron dan konsep larangan pauli yang dapat membedakan satu jenis elektron dengan elektron lainnya berdasarkan bilangan kuantum yang melekat pada setiap elektron. Elektron bebas secara kuantum memiliki sifat dualistic sebagai benda dan gelombang dapat bebas bergerak dalam seluruh volume kristal sebagai gelombang deBroglie. Syarat batas Born-von Karmann yang harus dipenuhi adalah: e ikx L e ik y L e ikz L 1 L disini adalah rusuk kristal dan kx, ky, kz adalah vektor vektor propagasi gelombang pada arah x, y, dan z. Masing-masing vektor propagasi tersebut dapat dijabarkan sbb: 2 En k x2 k y2 k z2 2 m0 m0 adalah massa elektron bebas Jumlah keadaan eleketron persatuan volume dengan energi antara E dan E E adalah : 3 1 2m0 2 2 g ( E )E E E 2 2 2 1 Jadi rapat keadaan elektron adalah 3 1 2m0 2 2 g (E) E 2 2 2 1 Konsep rapat elektron ini adalah salah satu konsep penting ketika akan merumuskan kapasitas panas yang berasal dari kontribusi elektron bebas. Larangan Pauli Larangan Paulimenyatakan bahwa tidak ada dua atau lebih elektron dalam satu sistem memilki ennergi dan bilangan kuantum yang tepat sama. Larangan Pauli dapat di jabarkan oleh Fermi Dirac sbb: f (E) 1 E EF 1 exp k BT Statistik Fermi Dirac memunculkan konsep energi Fermi yang merupakan jumlah energi yang dimiliki suatu kristal pada keadaan 0 K. Pada T = 0 K, f(E) = 1, sedangkan pada T selain 0 nilai dapat ditunjukkan dari persamaan diatas. Jumlah elektron per satuan volume pada T = 0 dapat dituliskan sbb: 3 1 2 m0 E F 0 2 n 3 2 2 Energi total yang dimiliki elektron pada T = 0 dapat dituliskan sbb: Ek E g ( E ) f ( E )dE 0 Karena 3 1 2m0 2 2 g ( E )dE E dE 2 2 2 1 Maka 3 3 1 5 1 2m0 2 2 1 2m 0 2 2 g ( E )dE E dE EF 0 2 2 2 5 2 2 3 1 2m E 2 3 Dengan mensubtitusikan nilai n 2 0 2 F 0 maka akan diperoleh E nE F 0 5 3 Dari persamaan tersebut dapat terlihat bahan elektron dengan harga energi sekitar EF dapat berperan pada analisis CV_elektron. Dalam analisis selnjutnya perlu tinjauan lebih detail tentang fungsi Fermi-Dirac tentang energi. Hal ini disebabkan dalam bahasan energi kinetik elektron bebas fungsi Fermi-Dirac terdapat dalam persamaaan energi kinetik yang sbb: Ee Ek 1 f E g ( E )E F E dE 0 f E g ( E )E F E dE Ek k dEe dF dF g ( E )E F E dE g ( E )E F E dE dT dT dT 0 Ek E Cv_elektron dF Cv_elektron g ( E )E E F dE dT 0 Pada suhu rendah k BT 1 EF m E EF k BT dF E E F e 2 E EF dT k BT k T 1 e B 2 Dengan mmemisalkan x = E EF maka persamaan kapasitas panas hasil kontribusi k BT elektron bebas dapat disederhanakan menjadi Cv_elektron g ( E )k B2T e x 2e x x 1 2 dx 2 3 g ( E )k B2T 2 k B2 2E F T Sehingga Cv= Cv_fonon + Cv_elektron = BT3 + AT, dengan A dan B adalah konstanta yang diperoleh dari perumusan Cv_elektron dan Cv_fonon. 5.3 Perilaku Elektron Bebas dalam Logam walaupun pada model elektron bebas klasik tidak dapat merumuskan dengan benar. konsep kapasitas panas, tetapi model ini berhasil menjelaskan pengaruh keberadaan elektron bebas terhadap sifat listrik sperti nilai tahanan jenis listrik (konduktifitas termal) dari bahan yang memiliki elektron bebas didalam kristal pembentuknya. elektron bebas bergerak sepanjang bahan memiliki panjang L dan luas penampang A akan memunculkan konsep arus listrik (I). pada bahan yang mengalir arus listrik akan timbul medan listrik (E). arus listrik yang mengalir dalam suatu panampang memunculkan nilai 𝐼 kerapatan (𝐽 = 𝐴). hukum ohm menyatakan hubungan antara kerapatan arus listrik dengan medan listrik sbb: 𝐽 = 𝜎. 𝐸 𝜎 adalah besaran yang menunjukkan konduktivitas dari bahan. besar konduktifitas adalah berbanding terbalik dengan nilai hambatan (resistivitas) : 1 𝜎 𝜌. nilai hambatan suatu bahan ditentukan oleh geometri dari bahan itu sendiri. resistivitas merupakan besaran pembanding antara nilai resistansi dengan faktor geometri dari 𝐿 suatu bahan (𝑅 = 𝜌 𝐴) resistivitas listrik pada pembahasan sebelumnya mengatakan bahwa resistivitas listrik berbanding terbalik dengan nilai konduktivitsnya. hambatan yang memunculkan nilai resistivitas dapat disebabkan oleh dua faktor yaitu adanya vibrasi kisi yang menyebabkan tumbukan anatara elektron bebas dengan fonon dan adanya ketidak murnian (impuritas). maka nilai resistivitas dapat dituliskan sebagai penjumlahan antara kedua komponen tersebut 𝜌 = 𝜌𝑓 + 𝜌𝑖 pada suhu rendah (T<<) nilai resistivitas hanya bergantung pada nilai umpuritas batas.