SOAL FISIKA LES

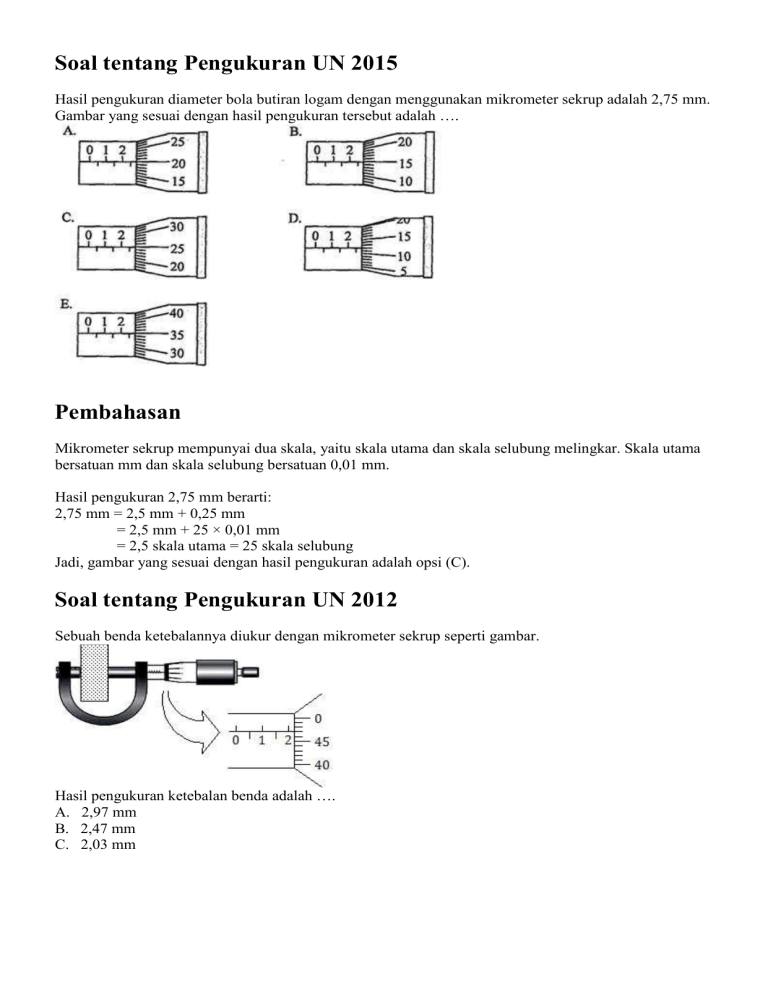
Soal tentang Pengukuran UN 2015
Hasil pengukuran diameter bola butiran logam dengan menggunakan mikrometer sekrup adalah 2,75 mm.
Gambar yang sesuai dengan hasil pengukuran tersebut adalah ….
Pembahasan
Mikrometer sekrup mempunyai dua skala, yaitu skala utama dan skala selubung melingkar. Skala utama
bersatuan mm dan skala selubung bersatuan 0,01 mm.
Hasil pengukuran 2,75 mm berarti:
2,75 mm = 2,5 mm + 0,25 mm
= 2,5 mm + 25 × 0,01 mm
= 2,5 skala utama = 25 skala selubung
Jadi, gambar yang sesuai dengan hasil pengukuran adalah opsi (C).
Soal tentang Pengukuran UN 2012
Sebuah benda ketebalannya diukur dengan mikrometer sekrup seperti gambar.
Hasil pengukuran ketebalan benda adalah ….
A. 2,97 mm
B. 2,47 mm
C. 2,03 mm
D. 1,97 mm
E. 1,47 mm
Pembahasan
Hasil pengukuran mikrometer sekrup tersebut adalah sebagai berikut:
skala utama = 2 mm
skala selubung = 47 × 0,01 mm = 0,47 mm
hasil pengukuran = skala utama + skala selubung
= 2 mm + 0,47 mm
= 2,47 mm
Jadi, hasil pengukuran ketebalan benda tersebut adalah 2,47 mm (B).
Soal tentang Pengukuran UN 2013
Gambar berikut ini menunjukkan hasil pembacaan skala pengukuran diameter bola kecil dengan
menggunakan mikrometer sekrup.
Hasil pengukurannya adalah ….
A. 6,93 mm
B. 6,94 mm
C. 6,95 mm
D. 6,86 mm
E. 6,97 mm
Pembahasan
Hasil pengukuran dengan mikrometer sekrup tersebut adalah sebagai berikut:
skala utama = 6,5 mm
skala selubung = 44 × 0,01 mm = 0,44 mm
hasil pengukuran = skala utama + skala selubung
= 6,5 mm + 0,44 mm
= 6,94 mm
Jadi, hasil pengukuran diameter bola kecil tersebut adalah (B).
Soal tentang Pengukuran UN 2009
Sebuah balok diukur ketebalannya dengan jangka sorong. Skala yang ditunjukkan dari hasil pengukuran
tampak pada gambar.
Besarnya hasil pengukuran adalah ….
A. 3,19 cm
B. 3,14 cm
C. 3,10 cm
D. 3,04 cm
E. 3,00 cm
Pembahasan
Jangka sorong terdiri dari dua skala, yaitu skala utama dan skala nonius (tambahan). Skala utama berada
di atas dengan satuan cm. Sedangkan skala nonius berada di bawah dengan satuan 0,01 cm.
Pada gambar di atas, angka 0 pada skala nonius berada di antara 3,1 dan 3,2 skala utama, berarti skala
utamanya adalah 3,1 cm. Garis pada skala nonius yang berimpit dengan garis pada skala utama adalah
garis ke-9 sehingga pembacaan skala noniusnya 9 × 0,01 cm = 0,09 cm.
Hasil pengukuran = skala utama + skala nonius
= 3,1 cm + 0,09 cm
= 3,19 cm
Jadi, hasil pengukuran ketebalan balok tersebut adalah 3,19 cm (A).
Soal tentang Pengukuran UN 2014
Perhatikan hasil timbangan dengan neraca Ohaus tiga lengan berikut!
Massa benda yang ditimbang adalah ….
A. 546,6 gram
B. 464,5 gram
C. 456,5 gram
D. 364,5 gram
E. 346,5 gram
Pembahasan
Neraca Ohaus terdiri dari tiga lengan. Lengan pertama berskala ratusan gram, lengan kedua berskala
puluhan gram, dan lengan ketiga berskala satuan gram. Pembacaannya adalah sebagai berikut:
lengan 1 : 400 gram
lengan 2 : 50 gram
lengan 3 : 6,5 gram
————————— +
total
: 456,5 gram
Jadi, hasil penimbangan massa benda tersebut adalah 456,5 gram (C).
Simak juga, Pembahasan Soal UN: Vektor Resultan.
SOAL FISIKA TENTANG GERAK
SOAL NO 1
Irfan menembakkan peluru dengan kecepatan awal 120 m/s membentuk sudut elevasi 30° terhadap permukaan
tanah. Jika g = 10 m/s2, peluru mencapai titik tertinggi setelah ….
a. 4 s
b. 5 s
c. 6 s
e. 7 s
d. 8 s
Jawaban : C
Pembahasan :
Vo = 120 m/s
θ = 30°
Waktu untuk mencapai titik tertinggi = tp
Jadi waktu yang diperlukan untuk mencapai puncak atau titik tertinggi adalah 6 sekon.
SOAL NO 2
Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum yang dicapai
peluru adalah ....
a. 30 m
b. 45 m
c. 50 m
d. 90 m
e. 100 m
Jawaban : B
Pembahasan :
Vo = 60 m/s
θ = 30°
Ketinggian maksimum = hmax
Jadi ketinggian maksimum yang dicapai peluru adalah 45 m.
SOAL NO 3
Seorang pemain sepakbola menendang bola dengan sudut elevasi 60°. Jika bola bergerak dengan kecepatan awal
30 m/s, maka jarak pemain yang menerima umpan kiper tersebut mendekati ....
a. 60 m
b. 65 m
c. 70 m
d. 75 m
e. 78 m
Jawaban : E
Pembahasan :
Vo = 30 m/s
θ = 60°
Arak horizontal maksimum = Xmax
Jadi jarak pemain yang menerima umpan kiper adalah 78 m.
SOAL NO 4
Sebuah benda dijatuhkan dari pesawat terbang yang melaju horisontal dengan kelajuan 360 km/jam pada
ketinggian 4500 m. Benda akan jatuh pada jarak horisontal sejauh (g = 10 m/s2) ....
A. 1.000 m
B. 2.000 m
C. 2.400 m
D. 3.000 m
E. 4.000 m
Jawaban : D
Pembahasan :
Vo = 360 km/jam = 100 m/s
h = 4500 m
X = ................?
“INGAT : Gerak setengah parabola, Gerak vertikal ke bawah = Gerak jatuh bebas dan Gerak horizontal = Geral
Lurus Beraturan”.
Jadi benda tersebut atuh pada jarak 3000 m dari jarak horizontal pesawat.
SOAL NO 5
Apabila besar sudut antara arah horizontal dan arah tembak suatu peluru adalah 53°, perbandingan antara jarak
tembak dalam arah mendatar dengan tinggi maksimum peluru adalah .... (sin 53° = 4/5 )
a. 2 : 3
b. 3 : 2
c. 3 : 1
d. 1 : 3
e. 2 : 1
Jawaban : C
Pembahasan :
Jadi perbandingan jangkauan maksimum dan ketinggian maksimum adalah 3 : 1
SOAL NO 6
Seorang pengemudi mobil offroad hendak melewati sebuah rintangan berupa parit sepanjang 7,5 m dengan
perbedaan ketinggian sebesar 1,8 m. Maka kecepatan mobil minimum agar mobil tidak masuk ke dalam parit
adalah .....
a. 7,5 m/s
b. 10 m/s
c. 12,5 m/s
d. 15 m/s
e. 20 m/s
Jawaban : C
Pembahasan
Jadi kecepatan minimum mobil agar tidak masuk ke dalam parit adalah 12,5 m/s
Soal tentang Gerak Parabola UNAS 2004
Sebuah peluru meriam ditembakkan dengan kecepatan awal 60 m/s dan sudut elevasi 53°. Bila g = 10
m/s2 maka posisi peluru pada detik ke-1 adalah ….
A. x = 36 m, y = 64 m
B. x = 64 m, y = 43 m
C. x = 36 m, y = 43 m
D. x = 32 m, y = 32 m
E. x = 43 m, y = 36 m
Pembahasan
Data-data yang diketahui pada soal:
vo = 60 m/s
g = 10 m/s2
t =1s
α = 53°
Sudut α = 53° merupakan sudut segitiga siku-siku yang bisa digambarkan sebagai berikut:
Gerak horizontal pada gerak parabola merupakan gerak lurus beraturan (GLB), sehingga:
x = vo cos α . t
= 60 . cos 53° . 1
= 60 . 3/5 . 1
= 36
Sedangkan gerak vertikal pada gerak parabola merupakan gerak lurus berubah beraturan (GLBB),
sehingga:
y = vo sin α − ½gt2
= 60 . sin 53° − ½ . 10 . 12
= 60 . 4/5 − 5
= 48 − 5
= 43
Jadi, posisi peluru pada detik ke-1 adalah x = 36 m, y = 43 m (C).
Soal tentang Gerak Parabola UN 2015
Sebuah bola ditendang dengan lintasan seperti pada gambar di bawah ini.
Tinggi maksimum bola adalah …. (g = 10 m/s2)
A. 10 m
B. 10√2 m
C. 20 m
D. 20√2 m
E. 40 m
Penyelesaian
Data-data yang diketahui pada soal:
g = 10 m/s2
vo = 20√2 m/s
vo2 = 800 m2/s2
α = 45°
sin α = ½√2
sin2 α = (½√2)2
=½
Tinggi maksimum bola dirumuskan sebagai:
= 20
Jadi, tinggi maksimum bola tersebut adalah 20 m (C).
Soal tentang Gerak Parabola UNAS 2005
Sebuah benda dilempar dengan kecepatan awal vo dan sudut elevasi 60°. Ketika benda mencapai tinggi
maksimum, jarak mendatar yang ditempuhnya 10√3 meter. Kecepatan awal benda tersebut adalah ... m/s.
A. 10√3
B. 20
C. 40
D. 20√3
E. 40√3
Jawab
Data-data yang diketahui pada soal:
x = 10√3 m
α = 60°
sin 2α = sin 120°
= sin (180 − 60)°
= sin 60°
= ½√3
Jarak mendatar ketika benda mencapai tinggi maksimum sama dengan setengah jarak tempuh maksimum.
x = ½ xm
vo2 = 400
vo = 20
Jadi, kecepatan awal benda tersebut adalah 20 m/s (B).
Soal tentang Gerak Parabola UNAS 2003
Sebuah peluru ditembakkan dengan kecepatan 40 m/s. Jika sudut elevasinya 60° dan percepatan
gravitasinya 10 m/s2 maka peluru mencapai titik tertinggi setelah ….
A. 1 sekon
B. √3 sekon
C. ½√3 sekon
D. 3 sekon
E. 2√3 sekon
Pembahasan
Data-data pada soal:
vo = 40 m/s
g = 10 m/s2
α = 60°
sin α = ½√3
Waktu yang diperlukan untuk mencapai tinggi maksimum dirumuskan:
= 2√3
Jadi, peluru tersebut mencapai titik tertinggi setelah 2√3 sekon (E).
Soal tentang Gerak Parabola UNAS 2008
Sebuah peluru dengan massa 20 gram ditembakkan pada sudut elevasi 60° dan kecepatan 40 m/s seperti
pada gambar.
Jika gesekan dengan udara diabaikan maka energi kinetik peluru pada titik tertinggi adalah ….
A. 0 joule
B. 4 joule
C. 8√2 joule
D. 12 joule
E. 24 joule
Penyelesaian
Data-data yang diketahui pada soal:
m = 20 gram = 0,02 kg
vo = 40 m/s
α = 60°
cos α = ½
Di titik tertinggi, kecepatan gerak peluru ke arah vertikal sama dengan nol (vy = 0) sehingga yang
berperan hanya kecepatan ke arah horizontal (vx).
vx = vo cos α
= 40 . cos 60° m/s
= 40 . ½ m/s
= 20 m/s
Energi kinetik di titik tertinggi adalah
Ek = ½mvx2
= ½ . 0,02. 202
=4
Jadi, energi kinetik peluru di titik tertinggi adalah 4 joule (B).
Pembahasan soal gerak vertikal ke bawah
Dibawah ini merupakan pembahasan soal-soal fisika tentang gerak vertikal kebawah. Gerak vertikal
kebawah adalah salah satu contoh gerak lurus berubah beraturan dipercepat. Jadi bahasan ini merupakan
materi pelajaran kelas X SMA semester ganjil. Oke langsung saja bisa disimak pembahasannya dibawah
ini.
Nomor 1
Bola dilempar vertikal kebawah dari sebuah bangunan bertingkat dengan kelajuan awal 10 m/s dan tiba
ditanah setelah 2 sekon. Kelajuan bola ketika menyentuh tanah adalah...
a. 10 m/s
b. 20 m/s
c. 30 m/s
d. 40 m/s
e. 50 m/s
Pembahasan:
Diketahui:
v0 = 10 m/s
t = 2 sekong = 10 m/s2
Ditanya: v = ...
Jawab: gunakan rumus 1.v = v0 + g . t = 10 m/s + 10 m/s2 . 2 s = 10 m/s + 20 m/s = 30 m/s
Jawaban: b
Nomot 2
Batu dilempar ke dalam sumur dengan kelajuan awal 5 m/s dan menyentuh permukaan air setelah 2
sekon. Kedalaman sumur adalah...
a. 10 m
b. 20 m
c. 30 m
d. 40 m
e. 50 m
Pembahasan:
Diketahui:
v0= 5 m/s
t=2s
g = 10 m/s2
Ditanya: h = ?
Jawab: (gunakan rumus 2)
h = v0 . t + ½ . g . t2
h = 5 m/s . 2 s + ½ . 10 m/s2 . (2s)2 = 10 m + 5 m/s2 . 4 s2 = 10 m + 20 m h = 30 m
Jawaban: c
Nomor 3
Bola A berada pada ketinggian 60 m vertikal diatas bola B. Pada saat yang bersamaan bola A dilepas
sedangkan bola B dilemparkan vertikal ke atas dengan kecepatan 20 m/s. Bola A dan bola B bertemu
pada saat:
1) Laju keduanya sama
2) Bola B turun
3) Dua sekon setelah bola A dilepas
4) 15 meter di atas posisi B mula-mula
Pernyataan yang benar adalah...
a. 1, 2, dan 3
b. 1 dan 3
c. 1, 2, 3, dan 4
d. 2 dan 4
e. 4 saja
Pembahasan
Waktu kedua bola bertemu:
s1 + s2 = 60 m
v0 . t1 – ½ . g . t12 + ½ . g . t22 = 260 m
20 m/s . t1 – ½ . 10 m/s2 . t12 + ½ . 10 m/s2 t12 = 60 m
20 m/s . t1 = 60 m
t1 = 3 s
Kecepatan bola A:
vA = g . t = 10 m/s2 . 3 s = 30 m/s
Kecepatan bola B
vB = v0 – g . t = 20 m/s – 10 m/s2 . 3 s = - 10 m/s (Bola B turun)
Ketinggian kedua bola ketika bertumbukan:
h = v0 . t – ½ . g . t2 = 20 m/s . 3 s – ½ . 10 m/s2 . (3 s)2 = 60 m – 45 m
h = 15 m
SOAL NO 1
Seseorang berdiri di pinggir jalan, sebuah mobil bergerak menjauhi orang tadi dengan kecepatan 20
m/s sambil membunyikan klakson yang berfrekuensi 400 Hz. Jika cepat rambat bunyi di udara pada
saat itu 380 m/s. maka frekuensi klakson yang didengar oleh orang tadi adalah ....
A. 340 Hz
B. 360 Hz
C. 380 Hz
D. 400 Hz
E. 420 Hz
Jawaban : C
Pembahasan :
Vs = 20 m/s menjauh (bertanda + )
fs = 400 Hz
Vp = 0 (diam)
V = 380 m/s
Maka fp adalah
Jadi frekuensi yang didengar oleh orang yang berdiri adalah 380 Hz
SOAL NO 2
Kereta bergerak A dengan kelajuan 72 km/jam dan kereta B dengan kelajuan 90 km/jam bergerak
saling mendekati. Masinis kereta A membunyikan peluit dengan frekuensi 660 Hz. Jika kecepatan
rambat bunyi di udara 350 m/s, maka frekuensi yang didengar masinis B dari peluit A adalah …
A. 800 Hz
B. 750 Hz
C. 600 Hz
D. 540 Hz
E. 400 Hz
Jawaban : B
Pembahasan :
Kereta A = sumber bunyi, Kereta B = pendengar
Vs = VA = 72 km/jam = 20 m/s mendekati pendengar ( + )
Vp = VB = 90 km/jam = 25 m/s mendekati sumber bunyi ( – )
fs = fA = 660 Hz
V = 350 m/s
VB = Vp yaitu :
Jadi frekuensi bunyi yang didengar oleh Masinis kereta B adalah 750 Hz
SOAL NO 3
Sebuah truk bergerak dengan kecepatan 25 m/s dibelakang sepeda motor. Pada saat truk
mengeluarkan bunyi klakson dengan frekuensi 945 Hz, pengemudi sepeda motor membaca pada
spidometer angka 20 m/s. Apabila kecepatan bunyi di udara 340 m/s, maka pengemudi sepeda
motor akan mendengar klakson dengan frekuensi .....
a. 750 Hz
b. 840 Hz
c. 945 Hz
d. 960 Hz
e. 1020 Hz
Jawaban : D
Pembahasan :
Sumber bunyi = truk, pendengar = motor
Vs = 25 m/s mendekati pendengar ( – )
Vp = 20 m/s menjauhi sumber ( – )
fs = 945 Hz
V = 340 m/s
Maka frekuensi yang didengar oleh pendengar motor
SOAL NO 4
Suatu sumber bunyi dengan frekuensi 720 Hz berlawanan arah dan menjauhi pendengar yang
bergerak dengan kelajuan 25 m/s, ternyata frekuensi bunyi yang didengar oleh pendengar adalah
630 Hz. Jika kelajuan perambatan bunyi di udara adalah 340 m/s, maka kecepatan sumber bunyi
adalah ....
A. 30 m/s
B. 25 m/s
C. 24 m/s
D. 20 m/s
E. 15 m/s
Jawaban : D
Pembahasan :
Dari soal di atas dapat diketahui bahwa sumber bunyi dan pendengar saling menjauh
fs = 720 Hz
fp = 630 Hz
Vp = 25 m/s menjauh ( – )
V = 340 m/s
Vs menjauh ( + )
Maka kecepatan sumber bunyi adalah
Jadi sumber buni bergerak dengan kelajuan 20 m/s
SOAL NO 5
Seorang pilot pesawat terbang bergerak mendekati bandara. Apabila pilot tersebut mendengar
bunyi sirine yang dipancarkan oleh menara pengawas dengan frekuensi 2000 Hz, dan cepat rambat
gelombang bunyi di udara 340 m/s, frekuensi sumber bunyi (sirine) 1700 Hz. Maka kelajuan
pesawat tersebut adalah .....
a. 20 m/s
b. 40 m/s
c. 60 m/s
d. 80 m/s
e. 100 m/s
Jawaban : C
Pembahasan :
fp = 2000 Hz
fs = 1700 Hz
V = 340 m/s
Vs = 0 (diam)
Vp mendekat ( + )
Maka kelajuan pendengar (pesawat) adalah
SOAL NO 6
Seorang pendengar berdiri di samping sumber bunyi yang frekuensinya 684 Hz. Sebuah sumber
bunyi lain dengan frekuensi 676 Hz bergerak mendekati pendengar itu dengan kecepatan 2 m/s.
Bila kecepatan merambat bunyi di udara 340 m/s, maka frekuensi layangan yang didengar oleh
pendengar itu adalah …
A. 2 Hz
B. 3 Hz
C. 4 Hz
D. 5 Hz
E. 6 Hz
Jawaban : C
Pembahasan :
f1 = 684 Hz
Vp = 0 (diam)
fs = 676 Hz
Vs = 2 m/s mendekat (–)
Maka bunyi yang didengar oleh pengamat dari sumber 2
Maka frekuensi layangan yang didengar pengamat adalah f = | f 1 – f2 | = | 684 – 680 | = 4 Hz
Pembahasan soal efek Doppler
Nomor 1
Dini berada di dalam kereta api A yang berhenti. Sebuah kereta api lain (B) bergerak mendekati A dengan
kecepatan 2 m.s−1 sambil membunyikan peluit dengan frekuensi 676 Hz. Bila cepat rambat bunyi di udara 340
m.s−1,maka frekuensi peluit kereta api B yang didengar Dini adalah....
A. 680 Hz
B. 676 Hz
C. 660 Hz
D. 656 Hz
E. 640 Hz
Pembahasan:
Diketahui:
vp = 0 (kereta berhenti)
vs = 2 m/s
fs = 676 Hz
v = 340 m/s
Ditanya: fp = ...
Jawab:
Nomor 2
Mobil pemadam kebakaran sedang bergerak dengan laju 20 m.s−1 sambil membunyikan sirine pada frekuensi 400
Hz (cepat rambat bunyi 300 m.s−1). Jika mobil pemadam kebakaran bergerak menjauhi seseorang yang sedang
berdiri di tepi jalan, maka orang tersebut akan mendengar frekuensi sirine pada frekuensi....
A. 375 Hz
B. 575 Hz
C. 600 Hz
D. 620 Hz
E. 725 Hz
Pembahasan:
Diketahui:
vs = 20 m/s
fs = 400 Hz
vp = 0 (pendengar diam)
v = 300 m/s
Ditanya: fp = ...
Jawab:
Nomor 3
Sebuah sumber bunyi bergerak dengan frekuensi 640 Hz bergerak mendekati seorang pengamat dengan
kecepatan 20 m/s. Jika cepat rambat bunyi di udara sebesar 340 m/s dan pengamat bergerak menjauhi searah
sumber bunyi dengan kecepatan 10 m/s, maka frekuensi bunyi yang di dengar oleh pengamat adalah...
A. 600 Hz
B. 660 Hz
C. 900 Hz
D. 980 Hz
E. 1.300 Hz
Pembahasan:
Diketahui:
vs = 20 m/s
fs = 640 Hz
vp = 10 m/s
v = 340 m/s
Ditanya: fp = ...
Jawab:
Nomor 4
Suatu kereta api bergerak dengan kecepatan 36 km/jam. Ketika akan melewati sebuah jembatan, kereta ini
membunyikan peluit dengan frekuensi 4950 Hz. Jika kecepatan perambatan bunyi 340 m/s maka frekuensi yang
terdengar oleh pendengar yang berada dijembatan adalah....
A. 5360 Hz
B. 5100 Hz
C. 4609 Hz
D. 4808 Hz
E. 4476 Hz
Pembahasan
Diketahui:
vs = 36 km/jam = 10 m/s
fs = 4950 Hz
v = 340 m/s
vp = 0
Ditanya: fp
Jawab:
fp = (v + vp) / (v - vs) fs
fp = (340 + 0) / (340 - 10) 4950 Hz
fp = 5100 Hz
CONTOH SOAL ELASTISITAS DAN PEMBAHASAN
Nomor 1 (UN 2012)
Untuk meregangkan sebuah pegas sejauh 5 cm diperlukan gaya sebesar 20 N. Energi potensial pegas ketika
meregang sejauh 10 cm adalah...
A. 2 joule
B. 4 joule
C. 20 joule
D. 50 joule
E. 100 joule
Pembahasan
Hitung terlebih dahulu konstanta pegas
k = F / x = 20 N / 0,05 m = 400 N/m
Menghitung energi potensial pegas
Ep = 1/2 k . x2
Ep = 1/2 . 400 N/m . 0,01 m = 2 joule
Jawaban: A
Nomor 2 (UN 2013)
Perhatikan grafik hubungan antara gaya (F) terhadap pertambahan panjang (x) berikut!
Manakah yang mempunyai konstanta terbesar?
Pembahasan:
A. k = B. k = F/x = 50 / 0,1 = 500 N/m
C. k = F/x = 5 / 0,1 = 50 N/m
D. k = F/x = 500 / 0,1 = 5000 N/m
E. k = F/x = 500 / 10 = 50 N/m
Yang terbesar adalah D = 5000 N/m
Nomor 3 (2010)
Karet yang panjangnya L digantungkan beban sedemikian rupa sehingga diperoleh data sebagai berikut:
Beban (W)
Pertambahan Panjang (ΔL)
2N
0,50 cm
3N
0,75 cm
4N
1,0 cm
Berdasarkan tabel tersebut dapat disimpulkan besar konstanta karet adalah...
A. 250 N/m
B. 360 N/m
C. 400 N/m
D. 450 N/m
E. 480 N/m
Pembahasan:
k = F/x = 2 N / 0,005 m = 400 N/m
Jawaban: C
Nomor 4
Pegas yang panjangnya L digantungkan beban sedemikian sehingga diperoleh data sebagai berikut:
Berdasarkan tabel tersebut, dapat disimpulkan besar konstanta pegas adalah...
A. 250 N/m
B. 360 N/m
C. 400 N/m
D. 450 N/m
E. 480 N/m
Pembahasan
Untuk menghitung konstanta pegas.
k = F / x = 4 N / 1,0 cm = 4 N / 0,01 m = 400 N/m
Jawaban: C
Nomor 5
Grafik hubungan antara gaya (F) terhadap penambahan panjang (Δx) suatu pegas ditunjukkan gambar dibawah.
Konstanta pegas yang digunakan adalah...
A. 1000 N/m
B. 900 N/m
C. 800 N/m
D. 700 N/m
E. 600 N/m
Pembahasan
Menghitung konstanta pegas dari grafik
k = F / x = 50 N / 0,05 m = 1000 N/m
Jawaban: A
Nomor 6
Grafik (F-x) menunjukkan hubungan antara gaya dengan pertambahan panjang pegas.
Besar energi potensial pegas berdasarkan grafik di atas adalah...
A. 20 joule
B. 16 joule
C. 3,2 joule
D. 1,6 joule
E. 1,2 joule
Pembahasan
Menghitung energi potensial pegas dari grafik:
Ep = 1/2 . F . x = 1/2 . 40 N . 0,08 m = 1,6 joule
Jawaban:
D
Nomor
7
Grafik dibawah menunjukkan hubungan antara gaya (F) dengan pertambahan panjang (Δx) sebuah pegas.
Energi
A.
B.
C.
D.
E.
potensial
pegas
pada
saat
mengalami
11,2
5,6
1,12
0,56
0,112
pertambahan
panjang
14
cm
Pembahasan
Menghitung energi potensial pegas dari grafik.
Ep = 1/2 . F . x = 1/2 . 8 N . 0,14 m = 0,56 joule
Jawaban: D
Nomor 8
Tiga pegas identik dengan konstanta 600 N/m disusun seperti gambar.
Jika susunan pegas diberi beban dengan berat w = 6 N, maka pertambahan panjang masing-masing pegas
adalah...
Pembahasan
adalah...
joule
joule
joule
joule
joule
Terlebih dahulu hitung konstanta gabungan:
Ktot = 600 / 3 = 200 N/m
Menghitung pertambahan panjang pegas.
x = F / Ktot = 6 N / 200 N/m = 0,03 m = 3 cm
Jadi pertambahan panjang masing-masing pegas = 1 cm (sebab 1 cm + 1 cm + 1cm = 3cm).
Jawaban: C
Nomor 9
Tiga pegas identik disusun seperti gambar dibawah.
Beban seberat 15 N digantung di ujung bawah pegas menyebabkan sistem pegas bertambah panjang 5 cm.
Konstanta masing-masing pegas adalah...
A. 15 N/m
B. 20 N/m
C. 45 N/m
D. 300 N/m
E. 900 N/m
Pembahasan
Menghitung Konstantan gabungan pegas.
Ktot = F / x = 15 N / 0,05 m = 300 N/m.
Menghitung
K = 3 . 300 N/m = 900 N/m
Jawaban: E
konstanta
masing-masing
pegas.
Nomor 10
Empat buah pegas masing-masing dengan konstanta c disusun secara paralel. Konstanta pegas dari susunan ini
menjadi...
A. 1/4 c
B. 1/2 c
C. 1 c
D. 2 c
E. 4 c
Pembahasan
Konstanta gabungan pegas susunan paralel
Ktot = c + c + c + c = 4c
Jawaban: E
Nomor 11
Empat pegas identik masing-masing memiliki konstanta 300 N/m disusun seperti gambar!
Konstanta gabungan keempat pegas adalah...
A. 150 N/m
B. 225 N/m
C. 300 N/m
D. 900 N/m
E. 1200 N/m
Pembahasan
Hitung terlebih dahulu tiga pegas yang disusun paralel (Kp)
Kp = 300 N/m + 300 N/m + 300 N/m = 900 N/m
Hitung
konstanta
gabungan
Ktot = 900 / 4 = 225 N/m
Jawaban: B
Nomor 12
Tiga buah pegas yang identik A, B, dan C dirangkai seperti gambar.
Jika ujung bebas C digantungi beban w = 1,2 N maka sistem mengalami pertambahan panjang 0,6 cm. Konstanta
masing-masing pegas adalah...
A. 200 N/m
B. 240 N/m
C. 300 N/m
D. 360 N/m
E. 600 N/m
Pembahasan
Hitung terlebih dahulu konstanta total
Ktot = F/x = 1,2 N / 0,006 m = 200 N/m
Menghitung
konstanta
masing-masing
pegas.
Ktot = (2/3) K = (2/3) . 200 N/m = 400/3 N/m
Jawaban: -
Nomor 13
Empat buah pegas identik masing-masing mempunyai konstanta 1600 N/m disusun seperti gambar.
Berat beban w yang digantung menyebabkan sistem pegas mengalami pertambahan panjang 5 cm. Berat beban w
adalah...
A. 60 N
B. 120 N
C. 300 N
D. 450 N
E. 600 N
Pembahasan
Hitung terlebih dahulu Konstanta gabungan pegas.
Ktot = (3/4) K = 3/4 . 1.600 N = 1200 N/m
Menghitung w = F.
F = Ktot . x = 1.200 N/m . 0,05 m = 60 N
Jawaban: A
Nomor 1 (UN 2012)
Agar gaya normal yang bekerja pada balok sebesar 20 N, maka besar dan arah gaya luar yang bekerja
pada balok adalah....
A. 50 N ke bawahB. 30 N ke atas
C. 30 N ke bawah
D. 20 N ke atas
E. 20 N ke bawah
Pembahasan:
ƩF = 0
N-w+F=0
20 N - 50 N + F = 0
- 30 N + F = 0
F = 30 N (karena positif berarti arah ke atas)
Jawaban: B
Nomor 2 (UN 2012)
Dua balok masing-masing bermassa 2 kg dihubungkan dengan tali dan katrol seperti gambar.
Bidang permukaan dan katrol licin. Jika balok B ditarik mendatar dengan gaya 40 N, percepatan balok
adalah...(g = 10 m/s2)A. 5 m/s2
B. 7,5 m/s2
C. 10 m/s2
D. 12,5 m/s2
E. 15 m/s2
Pembahasan:
Gunakan rumus:
Jawaban: A
Nomor 3 (UN 2013)
Sebuah balok dengan massa 20 kg diletakkan pada bidang miring kasar, ditarik dengan gaya sebesar F
dan percepatannya 3 m/s2.
Jika koefisien gesekan ɥ = 1/3 dan g = 10 m/s2, besar gaya F tersebut adalah...(sin 53 = 0,8)A. 260 N
B. 220 N
C. 160 N
D. 80 N
E. 60 N
Pembahasan:
Dari hukum II Newton:
F - w sin 53 - fg = m . a
F - 20 kg . 10 m/s2 . 0,8 - 1/3 . w cos 53 = 20 kg . 3 m/s2
F - 160 N - 1/3 . 20 kg . 10 m/s2 . 0,6 = 60 N
F - 160 N - 40 N = 60 N
F - 200 N = 60 N
F = 260 N
Jawaban: A
Nomor 4
Berikut adalah gambar yang menunjukkan lima buah benda yang diberikan gaya berbeda-beda.
Percepatan benda yang paling besar ditunjukkan oleh gambar nomor...
A. (1)
B. (2)
C. (3)
D. (4)
E. (5)
Pembahasan
Untuk menentukan percepatan benda yang paling besar gunakan hukum II Newton
A. a = F/m = 120 N / 20 N = 6 m/s2
B. a = F/m = 100 N / 10 kg = 10 m/s2
C. a = F/m = 150 N / 50 kg = 3 m/s2
D. a = F /m = 240 N / 80 kg = 3 m/s2
E. a = F/m = 200 N / 100 kg = 2 m/s2
Jawaban: B
Nomor 5
Sebuah benda bermassa 1 kg mula-mula bergerak mendatar dengan kecepatan 10 m/s. Kemudian diberi
gaya konstan 2 N selama 10 s searah dengan arah gerak benda. Besar kecepatan benda setelah 10 s
adalah...
A. 15 m/s
B. 20 m/s
C. 25 m/s
D. 30 m/s
E. 35 m/s
Pembahasan
Terlebih dahulu hitung percepatan dengan menggunakan hukum II Newton
a = F / m = 2 N / 1 kg = 2 m/s2
Menghitung kecepatan dengan menggunakan persamaan glbb
v = v0 + a . t = 10 m/s + 2 m/s2 . 10 s = 10 m/s + 20 m/s = 30 m/s
Jawaban: D
Nomor 6
Dua buah balok dihubungkan dengan seutas tali ringan di tarik secara horizontal dengan gaya F = 60 N.
Massa benda m1 = 20 kg dan m2 = 10 kg. Jika g = 10 m/s2 dan koefisien gesekan kinetis antara balok dan
permukaan lantai 0,1, maka besar percepatan kedua balok adalah...
A. 1 m/s2
B. 2 m/s2
C. 3 m/s2
D. 4 m/s2
E. 5 m/s2
Pembahasan
Menghitung percepatan 2 benda yang terletak pada bidang miring:
Jawaban: A
Nomor 7
Jika permukaan meja licin dan massa katrol diabaikan, maka sistem benda akan bergerak dengan
percepatan sebesar...
A. 5 m/s2
B. 10 m/s2
C. 16 m/s2
D. 25 m/s2
E. 40 m/s2
Pembahasan
Untuk menentukan percepatan kedua benda gunakan hukum II Newton seperti nomor 3
Jawaban: B
Nomor 8
Perhatikan gambar berikut!
Balok A mempunyai massa 2 kg dan balok B 1 kg. Balok B mula-mula diam dan kemudian bergerak ke
bawah. Bila g = 10 m/s2 maka tegangan tali yang menghubungkan kedua benda adalah...
A. 20,0 N
B. 10,0 N
C. 6,7 N
D. 3,3 N
E. 1,7 N
Pembahasan
Terlebih dahulu hitung percepatan kedua benda
Menghitung tegangan tali
T = W B - mB . a
T = 10 N - 1 kg . 10/3 m/s2 = 6,7 N
Jawaban: C
Nomor 9
Perhatikan gambar!
Benda A bermassa 8 kg terletak pada bidang datar dan dihubungkan dengan benda B bermassa 2 kg
melalui katrol. Benda B turun dengan kecepatan tidak tetap. Besar tegangan tali jika percepatan g = 10
m/s2 adalah...
A. 32 N
B. 20 N
C. 16 N
D. 10 N
E. 8 N
Pembahasan
Terlebih dahulu hitung percepatan kedua benda
Menghitung tegangan tali
T = W B - mB . a
T = 20 N - 2 kg . 2 m/s2 = 16 N
Jawaban: C
Nomor 10
Dua benda A dan B masing-masing bermassa 2 kg dan 6 kg diikat dengan tali melalui sebuah katrol yang
licin seperti gambar.
Mula-mula benda B ditahan kemudian dilepaskan. Jika g = 10 m/s2 maka tegangan tali yang
menghubungkan kedua benda adalah...
A. 5 N
B. 6 N
C. 10 N
D. 30 N
E. 60 N
Pembahasan
Hitung terlebih dahulu percepatan kedua benda
Menghitung tegangan tali
T = wB - mB . a = 60 N - 6 kg . 5 m/s2 = 30 N
Jawaban: D
Nomor 11
Sebuah balok ditahan dipuncak bidang miring.
Ketika dilepas balok meluncur tanpa gesekan sepanajang bidang miring. Kecepatan balok ketika
mencapai dasar bidang miring adalah..
A. 6 m/s
B. 8 m/s
C. 10 m/s
D. 12 m/s
E. 16 m/s
Pembahasan
Hitung terlebih dahulu percepatan
a = g sin 30o = 10 m/s2 . 1/2 = 5 m/s
Menghitung kecepatan menggunakan persamaan glbb
Jawaban: C
Nomor 12
Perhatikan gambar!
Sebuah balok kayu berada pada bidang miring kasar ditarik dengan gaya F = 200 N. Jika massa balok 18
kg dan percepatan 3 m/s2 maka gaya gesekan yang dialami balok terhadap bidang miring adalah...
A. 180 N
B. 126 N
C. 90 N
D. 56 N
E. 54 N
Pembahasan
Untuk benda pada bidang mirin berlaku persamaan
F - w sin 30o - fg = m . a
200 N - 180 N . 1/2 - fg = 18 kg . 3 m/s2
110 N - fg = 54 N
fg = 56 N
Jawaban: D
Nomor 13
Sewaktu berada didalam lift yang diam, berat sandi adalah 500 N. Sewaktu lift dipercepat keatas tegangan
tali menjadi 750 N. Jika g = 10 m/s2 maka percepatan lift adalah...
A. 5,0 m/s2
B. 7,5 m/s2
C. 10,5 m/s2
D. 12,5 m/s2
E. 15,0 m/s2
Pembahasan
Untuk lift yang bergerak ke atas berlakuT - w = m . a
750 N - 500 N = 50 kg . a
250 N = 50 kg . a
a = 250 N / 50 kg = 5 m/s2
Jawaban: A
Sebuah gelombang berjalan di permukaan air memenuhi persamaan y = 0,03 sin 2π (60 t − 2x), y dan x
dalam meter dan t dalam sekon. Cepat rambat gelombang tersebut adalah....
A. 15 m.s−1
B. 20 m.s−1
C. 30 m.s−1
D. 45 m.s−1
E. 60 m.s−1
(Soal Gelombang - UN Fisika 2011)
Pembahasan
Dengan cara yang sama nomor sebelumnya:
Soal pembahasan tentang gelombang yang lain silahkan dibuka berikut ini.
Soal No. 11
Pada tali yang panjangnya 2 m dan ujungnya terikat pada tiang ditimbulkan gelombang stasioner. Jika
terbentuk 5 gelombang penuh, maka letak perut yang ke tiga dihitung dari ujung terikat adalah...
A. 0,10 meter
B. 0,30 meter
C. 0,50 meter
D. 0,60 meter
E. 1,00 meter
(Soal Gelombang Stasioner Ujung Tetap - Ebtanas 1992)
Pembahasan
Terlihat, dalam 2 meter (200 cm) ada 5 gelombang. Jadi untuk 1 gelombangnya, panjangnya adalah
λ = 200 cm/5 = 40 cm.
Perut ketiga, jika dihitung dari ujung ikatnya berjarak 1 gelombang lebih 1/4, atau 5/4 gelombang. Jadi
jaraknya adalah:
x = 5/4 × λ
x = 5/4 × 40 cm = 50 cm = 0,5 meter.
Soal No. 12
Seutas tali digetarkan pada salah satu ujungnya sehingga menghasilkan gelombang seperti gambar.
Jika ujung tali digetarkan selama 0,5 s maka panjang gelombang dan cepat rambat gelombang berturutturut adalah….(Sampel UN 013)
A. 25 cm dan 100 cm/s
B. 25 cm dan 50 cm/s
C. 50 cm dan 25 cm/s
D. 50 cm dan 100 cm/s
E. 125 cm dan 25 cm/s
Pembahasan
Untuk dua buah gelombang = 50 cm
Jadi satu gelombangnya λ = 50 cm / 2 = 25 cm
Cepat rambat:
50 cm / 0,5 s = 100 cm/s