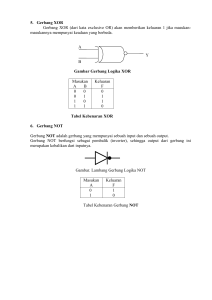
GERBANG LOGIKA DAN ALJABAR BOOLEAN Gerbang logika adalah rangkaian digital yang dapat dinyatakan dengan dua keadaan (tegangan/logika tinggi atau tegangan/logika rendah). Gerbang logika merupakan rangkaian dengan satu atau lebih sinyal masukan, tetapi hanya menghasilkan satu sinyal keluaran. Keluaran akan berlogika tinggi (1) atau berlogika rendah (0) tergantung pada sinyal masukan digital yang diberikan. Rangkaian digital di dalam computer digital dan system digital lainnya dirancang dengan menggunakan disiplin matematika, yaitu Aljabar Boole. Nama tersebut diambil dari nama penemunya yaitu George Boole. 1. Gerbang Logika Dasar Gerbang logika dasar ada tiga, yaitu : gerbang NOT (Inverter), gerbang AND, dan gerbang OR. a. Gerbang NOT (Inverter) Gerbang NOT adalah gerbang logika dasar yang mempunyai satu sinyal masukan dan satu sinyal keluaran, dimana keluarannya selalu berlawanan dengan masukannya. Apabila sinyal masukan berlogika 1, maka keluarannya akan berlogika 0, begitu sebaliknya. Jadi, gerbang NOT berfungsi sebagai inverter (pembalik) inputnya. Simbol gerbang NOT diperlihatkan pada Gambar 3.1. Untuk menggambarkan level output dari masing-masing kombinasi input dapat dibuat dengan menggunakan tabel kebenaran. Tabel 3.1 menunjukkan table kebenaran inverter. Persamaan logika atau fungsi aljabar boole untuk gerbang NOT adalah : Y= Operasi Inverter secara simbolis direpresentasikan dengan menggunakan garis diatas. Timing Diagram acap kali dibutuhkan untuk memudahkan dalam menganalisa kinerja suatu system. Gambar 3.2 berikut menggambarkan timing digram gerbang NOT. Dalam prakteknya, gerbang NOT disediakan dalam bentuk IC digital, dan salah satu jenisnya adalah IC TTL (Transistor-transistor Logic). Seri IC TTL untuk gerbang OR 2 input adalah 7404. IC 7404 menyediakan 6 buah gerbang NOT. Gambar IC dan susunan pin IC 7404 ditunjukkan pada gambar berikut. b. Gerbang AND Gerbang AND mempunyai dua atau lebih sinyal masukan tetapi hanya satu sinyal keluaran. Semua masukan harus dalam keadaan tinggi untukmendapatkan keluaran yang tinggi. Gambar 3.3 memperlihatkan simbol gerbang AND 2 input. Tabel kebenaran gerbang AND untuk kombinasi 2 masukan A dan B diperlihatkan pada Tabel 3.2. Persamaan logika atau fungsi aljabar untuk gerbang AND 2 input adalah : Y=A.B Operasi AND secara simbolis direpresentasikan dengan menggunakan operator titik (dot), dan boleh juga disederhanakan tanpa menggunakan titik (dot). Gambar 3.5 berikut menggambarkan timing digram gerbang AND 2 input. Dalam praktek, gerbang AND jenis TTL mempunyai nomor seri 7408. Gambar susunan pin IC 7408 seperti ditunjukkan pada gambar 3.6 berikut : c. Gerbang OR Gerbang OR mempunyai dua atau lebih sinyal masukan tetapi hanya satu sinyal keluaran. Jika salah satu atau semua sinyal masukannya tinggi, maka sinyal keluarannya akan menjadi tinggi. Simbol gerbang OR 2 input diperlihatkan pada Gambar 3.7. Tabel kebenaran gerbang OR untuk kombinasi 2 masukan A dan B diperlihatkan pada Tabel 3.3. Persamaan logika atau fungsi aljabar untuk gerbang OR 2 input adalah : Y=A+B Operasi OR secara simbolis direpresentasikan dengan menggunakan operator tambah (“+“). Gambar 3.8 berikut menggambarkan timing diagram gerbang OR 2 input. Dalam praktek, IC TTL untuk gerbang OR 2 input adalah 7432. Gambar susunan pin IC 7432 ditunjukkan pada gambar 3.9 berikut : 2. Gerbang Logika Lain 1. Gerbang NAND Gerbang NAND mempunyai dua atau lebih sinyal masukan tetapi hanya satu sinyal keluaran. Struktur logika gerbang NAND yang terdiri dari sebuah gerbang AND dan sebuah inverter yang dirangkai secara seri. Gerbang NAND merupakan kebalikan dari gerbang AND, dimana keluarannya akan rendah apabila semua masukannya berlogika tinggi. Simbol gerbang NAND 2 input diperlihatkan pada Gambar 3.10. Tabel kebenaran gerbang NAND untuk kombinasi 2 masukan A dan B diperlihatkan pada Tabel 3.4. Persamaan logika atau fungsi aljabar untuk gerbang NAND 2 input adalah : Y= Timing diagram gerbang NAND 2 input dapat dilihat pada Gambar 3.11 berikut : Dalam praktek, gerbang NAND disediakan dalam bentuk IC. Untuk jenis TTL, gerbang NAND serinya antara lain 7400 (NAND 2 input) dan 7410 (NAND 3 input). Berikut adalah susunan pin IC 7400. b. Gerbang NOR Gerbang NOR mempunyai dua atau lebih sinyal masukan tetapi hanya satusinyal keluaran. Struktur logika gerbang NAND yang terdiri dari sebuah gerbang OR dan sebuah inverter yang dirangkai secara seri. Gerbang NOR merupakan kebalikan dari gerbang OR. Untuk memperoleh keluaran yang tinggi dari gerbang NOR, semua masukan harus berada dalam keada an rendah. Dengan kata lain, gerbang NOR hanya mengenal kata masukan yang semua bitnya sama dengan nol. Simbol gerbang NOR 2 input diperlihatkan pada Gambar 3.13. Tabel kebenaran gerbang NOR untuk kombinasi 2 masukan A dan B diperlihatkan pada Tabel 3.5. Persamaan logika atau fungsi aljabar untuk gerbang NOR 2 input adalah : Y= Timing diagram gerbang NOR 2 input dapat dilihat pada Gambar 3.14 berikut : c. Gerbang EX-OR Gerbang EX-OR mempunyai dua atau lebih sinyal masukan tetapi hanya satu sinyal keluaran. Keluaran gerbang EX-OR akan menjadi tinggi bila salah satu masukannya berlogika tinggi (1). Dengan kata lain, keluaran 1 hanya terjadi bila masukannya berbeda. Hal ini dapat dilihat pada tabel 3.6 berikut : Berdasarkan tabel kebenaran di atas dapat dituliskan persamaan aljabarnya yaitu : Y= B+A Simbol logika untuk gerbang EX-OR 2 input adalah : Timing diagram gerbang EX-OR 2 input dapat dilihat pada Gambar 3.17 berikut : Dalam praktek, IC TTL untuk gerbang EX-OR mempunyai nomor seri 7486. Gambar berikut menggambarkan sususan pin IC 7486 : d. Gerbang EX-NOR Gerbang EX-NOR ekivalen dengan EX-OR yang diikuti oleh sebuah inverter, seperti yang ditunjukkan pada gambar berikut : Persamaan fungsi aljabarnya adalah : Y= + AB Keluaran gerbang EX-NOR akan tinggi bila semua masukannya sama, sehingga gerbang EX-NOR ini merupakan gerbang yang ideal untuk digunakan sebagai pembanding bit atau kata, dimana masukan dikenali oleh gerbang bila kedua bit masukannya identik. Contoh rangkaian pembanding kata : Rangkaian di atas adalah rangkaian pembanding kata (word comparator), yang mengenali 2 kata identik. Gerbang EX-NOR yang paling kiri membandingkan A3 dan B3, jika keduanya sama maka Y3 = 1, begitu juga untuk ketiga gerbang lainnya. Bila kata A dan B identik, maka seluruh gerbang EXNOR mempunyai keluaran tinggi dan keluaran akhir dari gerbang AND berupa sinyal EQUAL akan berlogika tinggi. Bila kata A dan B berbeda, maka sinyal EQUAL berlogika rendah.\ Gambar 3.21 memperlihatkan timing diagram gerbang EX-NOR 2 input. 3. Deskripsi Rangkaian Logika ke Persamaan Logika Rangkaian logika dapat dideskripsikan ke dalam bentuk persamaan logika atau ekspresi aljabar boole. Untuk memudahkan dalam mendeskripsikan atau membuat persamaan logika, tulislah terlebih dahulu persamaan logika pada setiap output gerbang penyusun rangkaian tersebut. Selanjutnya, penulisan persamaan logika terhadap gerbang terakhir, akan menghasilkan persamaan logika dari rangkaian tersebut. Contoh 3.1 Buatlah persamaan logika untuk rangkaian logika berikut ini : Jadi, persamaan logika dari rangkaian tersebut : Y= +B Contoh 3.2 Buatlah persamaan logika untuk rangkaian logika berikut ini : Sehingga : Y = A(B + C) 4. Membuat Tabel Kebenaran Suatu Rangkaian Logika Untuk membuat tabel kebenaran dari suatu rangkaian logika dapat dilakukan dengan 2 cara, yaitu : • Cara 1 : Menulis keluaran dari semua gerbang yang merupakan komponenpenyusun rangkaian logika untuk seluruh kombinasi input • Cara 2 : Mengevaluasi keluaran dari persamaan logika Membuat tabel kebenaran dengan cara 2 relatif lebih mudah dan cepat dilakukan dibandingkan dengan cara 1. Contoh 3.3 dan 3.4 diselesaikan dengan menggunakan cara 1, sedangkan contoh 3.5 diselesaikan dengan menggunakan cara 2. Contoh 3.3 Buatlah tabel kebenaran untuk gambar rangkaian yang ada pada contoh 3.1 ! Jawab : Persamaan logika untuk gambar rangkaian pada contoh 3.1 : Y = +B Tabel kebenaran untuk persamaan di atas : Contoh 3.4 Buatlah tabel kebenaran untuk gambar rangkaian yang ada pada contoh 3.2 ! Jawab : Persamaan logika untuk gambar rangkaian pada contoh 3.2 : Y = A(B+C) Tabel kebenaran untuk persamaan di atas : Contoh 3.5 Buatlah tabel kebenaran untuk gambar rangkaian berikut : Jawab : Persamaan logika dari rangkaian tersebut : Y = AB + CD Arti persamaan di atas : Y akan berlogika 1, jika AB = 1 atau CD = 1 AB = 1, jika A = 1 dan B = 1 CD = 1, jika C = 1 dan D = 1 Maka Y = 1 jika : A = 1 dan B = 1 atau C = 1 dan D = 1 Selain itu Y = 0 Sehingga bisa dibuat tabel kebenaran sebagai berikut : Dari contoh di atas, bisa dibayangkan repotnya jika kita membuat table kebenaran dengan cara mencari keluaran dari semua gerbang untuk seluruh kombinasi input. Jika input ada 3, maka kita akan mencari keluaran untuk 8 kombinasi input. Jika input ada 4, maka akan ada 16 kombinasi input. Jadi, untuk n input akan menghasilkan 2n kombinasi input. 5. Implementasi Rangkaian Logika Kemampuan mengimplementasikan rangkaian berdasarkan persamaan logika adalah sangat penting, karena setiap rancangan rangkaian logika akan menghasilkan persamaan logika, dan agar dapat dimanfaatkan dalam bentuk nyata maka persamaan tersebut perlu diimplementasikan atau direalisasikan. Contoh 3.6 Implementasikan persamaan logika Y = C + BC + A ke dalam bentuk rangkaian logika. Jawab : • Berdasarkan persamaan tersebut terlihat bahwa terdapat 3 suku persamaan yaitu C , BC dan A Ketiga suku tersebut dioperasikan dengan operator “tambah”, sehingga diperlukan gerbang 1 buah gerbang OR 3 input. • Selanjutnya, terlihat bahwa suku-suku persamaan merupakan operasi AND dari variable-variabel input, untuk suku-1 dan suku-2 memerlukan 2 buah gerbang AND 3 input, dan suku-3 memerlukan 1 buah gerbang AND 2 input. • Terdapat pula 4 buah operasi NOT, sehingga diperlukan 4 buah gerbang NOT Jadi rangkaian logikanya adalah :