fluks listrik

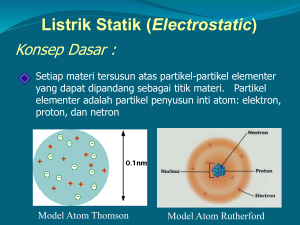
LISTRIK STATIS
A.
1.
INTERAKSI ELEKTROSTATIK
Muatan Listrik
elektron (bermuatan negatif)
lintasan elektron
inti atom
+
netron (tidak bermuatan)
+ +
ptoton (bermuatan positif)
-
-
atom

Atom terdiri dari inti atom bermuatan positif, dan
elektron-elektron bermuatan negatif bergerak
mengelilingi inti.
 Inti atom terdiri dari ptoton bermuatan positif dan
netron tidak bermuatan.
 Ada 2 jenis muatan listrik :
1. Muatan negatif, yaitu muatan yang
sejenis dengan muatan elektron.
2. Muatan positif, yaitu muatan yang tidak
sejenis dengan muatan elektron.
 Sifat muatan :
“ Muatan-muatan yang sejenis tolak menolak
dan muatan-muatan yang tidak sejenis tarik
menarik “
 Elektroskop ialah alat untuk mengetahui ada
atau tidak adanya muatan listrik.
 Cara memberi muatan listrik.
1. Dengan cara menggosok
2. Dengan cara menyentuhkan dengan benda
yang bermuatan
3. Dengan cara induksi
2.Gaya Coulomb.
 Gaya interaksi (gaya tarik/tolak) antara
dua buah muatan disebut gaya Coulomb
(gaya elektrostatis)
 Besar gaya Coulomb antara 2 muatan :
* berbanding lurus dengan kedua
muatan itu masing-masing.
* berbanding terbalik dengan kuadrat
jarak antara kedua muatan itu.
F
F
q
-
q’
r
+
q
q’
r
F
F
r
 F~q
 F~q’
 F~1/r2
+
q+
F
- q’
F
qq '
F~ 2
r
 Dirumuskan
:
qq'
F k 2
r
F = gaya coulomb ( N )
 q,q’ = muatan listrik ( Coulomb = C )
 r = jarak antara kedua muatan ( m )
 k = konstanta pembanding
= 1/4пεo = 9.109 Nm2C-2
 εo = permitivitas ruang hampa
= 8,85.10-12 CN-1m-2
 Permitivitas medium selain udara
disimbulkan ε, dan besar ε> εo
 Perbandingan ε/εo disebut konstanta
dielektrik (K) atau permitivitas relatif (εr )

 Grafik
gaya coulomb :
F
F
r2
 Jumlah
q1 +
dua gaya coulomb yg segaris:
F1 q’ F2
-
r1
r
r2
+ q2
F
= l F1 – F2 l

Bila kedua gaya coulomb saling membentuk
sudut :
q
q
'
1
- q2
F k
1
F
θ
F1
+
q’
F2
r2
r1
+
q1
2
2
r
q2 q '
F2  k 2
r2
F  F  F  2 F1 F2 cos 
2
1
2
1
B. MEDAN LISTRIK
1. Kuat medan listrik
 Medan listrik adalah daerah yang masih
terasa adanya pengaruh listrik.
 Pada muatan listrik yang diletakkan di
dalam medan listrik timbul gaya listrik.
 Ukuran medan listrik dinyatakan dengan
kuat medan listrik.
 Kuat medan listrik di suatu titik adalah
gaya listrik yang dialami oleh satu satuan
muatan positip di titik itu.

Muatan q menimbulkan medan listrik di
sekitarnya, perhatikan kuat medan listrik
di titik P
E
r
+
q
E
P
r
q
P

Kuat medan listrik di titik P ditumuskan :
q
Ek 2
r


Arah kuat medan listrik searah dengan
gaya yang dialami oleh satu satuan
muatan positip di titik itu.
Jika di titik P ada muatan q’, maka kuat
medan listrik tersebut adalah :



qq'
k 2
q
F
r
Ek 2 

r
q'
q'
Dapat dikatakan : kuat medan listrik di
suatu titik adalah gaya listrik per satuan
muatan positip di titik itu.
Bagaimana kuat medan listrik di suatu
titik yang dipengaruhi oleh dua medan
listrik ?
 Perhatikan
gambar berikut ini
E1
B
r1
q1 +
θ
E2
E
r2
E1
r1
A E2 r2
q2
Resultan kuat medan listrik di A :
E = l E1 + E2 l
 Resultan kuat medan listrik di B :

E  E  E  2 E1 E2 cos 
2
1
2
2
Medan listrik yang telah kita pelajari
adalah medan konserfatif
 Medan konserfatif adalah medan yang
arah kuat medannya di setiap titik selalu
menuju atau meninggalkan suatu titik
pusat.

Dua muatan q1 = 12 μC dan q2 = -28,45
μC berjarak 10 cm satu sama lain. Titik A
terletak di tengah-tengah kedua muatan
tersebut sedangkan titik B terletak pada
jarak 6 cm dari q1 dan 8 cm dari q2.
Hitunglah :
a. kuat medan listrik di titik A.
b. kuat medan listrik di titik B.
c. gaya coulomb yang dialami oleh
muatan 2 μC, bila muatan tersebut
diletakkan di titik A
d. gaya coulomb yang dialami oleh
muatan 2 μC, bila muatan tersebut
diletakkan di titik B
2. Hukum Gauss.
• Medan listrik dinyatakan dengan garis-
garis gaya (garis medan) listrik.
• Garis gaya (garis medan) listrik adalah
garis khayal yang merupakan kedudukan
titik-titik, dan kuat medan di setiap titik
pada garis tersebut selalu berimpit dengan
garis singgung di titik itu.
E
E
E
E
• Gambar garis medan
+
+
+
+



Bila jumlah garis-garis gaya listrik
semakin rapat menggambarkan bahwa
kuat medan listriknya semakin kuat.
Jumlah garis gaya listrik yang menembus
luasan secara tegak lurus disebut fluks
listrik.
Jumlah garis gaya listrik yang menembus
luasan secara tegak lurus tiap satu satuan
luas disebut kuat medan listrik.

E
An
atau ditulis
  An E
A

θ
A
Bila arah medan membentuk sudut θ
terhadap normal bidang, maka ditulis :
Φ = fluks listrik
Φ = AE cos θ
A = luas
E = kuat medan listrik
θ = sudut antara medan listrik dan
normal bidang.

Menurut Hukum gauss :
“Jumlah garis medan (fluks listrik)
yang melalui permukaan tertutup
berbanding lurus terhadap muatan
yang diselimuti permukaan tersebut”
  AE cos  
q
o

Perhatikan gambar berikut ini.
C
+++
Permukaan
Permukaan
Permukaan
Permukaan
A
B
++
+
+ +
++
D
A : masuk 4, keluar 4, jumlah 0
B : masuk 2, keluar 9, jumlah +7
C : masuk 2, keluar 0, jumlah -2
D : masuk 2, keluar 1, jumlah -1

Contoh penerapan hukum Gauss
1. Medan listrik antara dua keping konduktor
sejajar yang bermuatan

++
++
++
++
++
+
-- -- --
Tiap keping bermuatan sama,
yaitu q dan –q.
 Luas tiap keping = A
 Rapat muatan tiap keping
σ = q/A
 Menurut Hukum Gauss :
Φ = EAcosθ = q/εo maka :

E = σ/εo.
2. Medan listrik akibat bola konduktor bermuatan
H
R
I

Muatan tersebar merata
di permukaan bola
 Untuk r<R (luasan I) :
E = q/ εo A cos 0o = 0
 Untuk r≥R (luasan H) :
E = q/ εo A cos 0o
= q/ Aεo = q/4пr2 εo
= (1/4пεo )(q/ r2 )
E = k q/r2

Grafik E - r
O R
E
E= 0
E = k q/r2
r
C.ENERGI POTENSIAL DAN POTENSIAL
LISTRIK
1. Energi potensial listeik.
F
q’
A + F’cosθ
F’θ
r
A
q
rB
B

Muatan q’ berada di
dalam medan listrik
yang ditimbulkan
oleh muatan q, dan
dipindahkan dari
titik A yang
berjarak rA ke titik
B yang berjarak rB
terhadap q.
F
q’
A + F’cosθ
F’θ
r
A
q
rB
B
Untuk mengimbangi
gaya coulomb F
diperlukan gaya
F’=-F =-kqq’/r2.
 Untuk memindahkan
muatan dari A ke B
diperlukan usaha :

rB
rB
rA
rA
WAB   F ' cos ds   F ' ds cos 
ds cos  dr
rB
qq '
WAB    k 2 dr
r
rA
rB
1
WAB  kqq' 
r  rA
1 1
WAB  kqq'   
 rB rA 
WAB
qq'
qq'
k
k
rB
rA
Karena WAB = EpB – EpA,
maka :
qq '
Ep A  k
rA
qq '
EpB  k
rB
secara umum ditulis :
qq '
Ep  k
r

Bila muatan q’ dipindah dari titik A jauh
takterhingga ke titik B, maka :
WAB

 1 1
qq'
 kqq'     k
rB
 rB ~ 
Dapat dikatakan bahwa :“Energi potensial
listrik di suatu titik adalah usaha yang
diperlukan untuk memindahkan muatan
q’ dari jauh tak terhingga ke titik itu.”
2. Potensial listrik.

Potensial listrik ialah energi potensial
listrik per satu satuan muatan
qq'
k
Ep
q
r
V

k
q'
q'
r
q'
V k
r
V = potensial listrik ( volt = V)
 Karena energi potensial listrik besaran
skalar maka potensial listrik juga besaran
skalar.

• Potensial listrik akibat
beberapa muatan
-q3
3.Hubungan energi
potensial dan
potensial listrik.
r3
+
r1
P r2
+
+q2
WAB
qq'
qq'
k
k
rB
rA
WAB
 q
q
 q'  k  k 
rA 
 rB
+q1
• Potensial listrik di titik P
V  V1  V2  V3
 q1 q2 q3 
V  k  
 
r3 
 r1 r2
• Secara umum ditulis :
q
V  k
r
WAB  q' VB  VA 
4. Hukum kekekalan energi mekanik.

Karena medan listrik merupakan medan
konserfatif, maka berlaku hukum
kekekalan energi mekanik.
Ep1 + Ek1 = Ep2 + Ek2
atau
qV1 + ½ mv12 = qv2 + ½ mv22

Usaha yang dilakukan untuk
memindahkan muatan q’ adalah
W = q(V1 – V2) = ½ mv22 – ½ mv12
3.Energi potensial dan potensial listrik pada
keping konduktor.
F

q’ F’
+θ
A

+
+
+
+
+
+
+
+
+
B+

Muatan q’ mendapat
gaya F = q’E.
Untuk memindahkan
muatan q’ dari A ke B
harus diimbangi
dengan gaya :
F’ = -F = -q’E.
d
Usaha untuk memindahkan muatan q’ dari
A ke B adalah : WAB = -F’ cos θ SAB.



WAB = -q’E cos θ SAB
WAB = -q’E SAB Cos θ
WAB = -q’Ed



WAB = EpB - EpA
WAB = -q’Ed
EpB – EpA =-q’Ed
4.Hubungan potensial dengan kuat medan
listrik.
V AB
E
 WAB = -q’Ed = q’VAB
d
B
d
q’ +  E = kuat medan listrik ( NC-1 )
++
+  VAB = beda potensial listrik (volt)
+
+  d = jarak antara kedua keping ( m )
+
+
A
VAB
• Dua titik berjarak r di antara dua keping,
•
dan r < d memiliki beda potensial :
V = Er = σr/εo
Bola konduktor bermuatan
B
A
R
B
R
A
O
• Untuk memindahkan muatan q dari O ke A
•
diperlukan usaha : WOA = qER = q(VO – VA)
Karena E = 0, maka VO - VA = 0 atau VO = VA
• Dapat disimpulkan :
* Untuk r < R,
V = kq/R
* Untuk r > R,
V = kq/r
• Grafik V - r
O R
V
V = k q/r
r
E
E= 0
E = k q/r2
r