Judul - Binus Repository

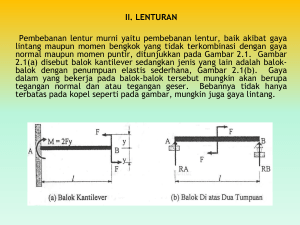
Matakuliah
Tahun
Versi
: R0262/Mekanika Teknik
: September 2005
: 1/1
Pertemuan 22
Tegangan Lentur dan Puntir pada
Balok
1
Learning Outcomes
Pada akhir pertemuan ini, diharapkan mahasiswa
akan mampu :
• menghitung tegangan lentur, aksial dan puntir
pada balok berdasarkan hukum hook
2
Outline Materi
• Pengertian tegangan pada balok struktur
• Jenis tegangan
• Tegangan gabungan
3
Tegangan Lentur dan Puntir pada
Balok Struktur
•
Tegangan ialah suatu satuan yang timbul dari
kekuatan bahan konstruksi yang merupakan
kemampuan dari balok konstruksi terhadap
gaya - gaya luar yang bekerja padanya.
•
Besarnya tegangan sangat dipengaruhi oleh
jenis bahan konstruksi, gaya luar yang
diterjemahkan ke gaya dalam, bentuk serta
besaran dari penampang bahan konstruksi
tersebut.
4
• Jenis Tegangan :
– Tegangan lentur (akibat momen)
– Tegangan axial / normal (akibat gaya axial)
– Tegangan geser (akibat gaya lintang)
– Tegangan puntir (akibat gaya eksentris)
5
• Tegangan lentur et 
– Yaitu tegangan yang ditimbulkan oleh balok
akibat beban/gaya yang bekerja diatas balok
tersebut.
Simbol tegangan = 
% t/m
A
B
6
– Balok dibebani beban terbagi rata % t/m,
maka balok tersebut akan melentur seperti
gambar diatas.
– Serat atas tertekan dan serat bawah tertarik
– Rumus
M. Y
τ
Ι
kg
cm2
7
M = Momen yang bekerja pada garis berat
(momen gaya dalam)
Y = Jarak tegangan dari garis berat
penampang (cm)
I = Momen Inersia penampang (cm4)
– Garis netral pada tegangan lentur yaitu garis
yang memotong penampang dimana
tegangan lentur pada titik potong tersebut = 0
8
Contoh tegangan lentur pada suatu balok :
q = 2 t/m'
20 cm
P = 1t
30 cm
  6m
Mencari tegangan lentur maximum  M max
9
Penyelesaian : VA  VB  1 Q  6 ton ()
2
1
Mmax  VA . X  q . x . x
2
dMx
0
dx
V A  qx  0
6  2x  0
x
3
1
Momen max  VA.3  .2.3 2
2
9tm
10
20 cm
τa
X
30
(10,15)
Garis
netral
b
Y
11
Titik berat benda (10,15)
Jarak titik berat ke sumbu atas Ya = 15 cm
Jarak titik berat ke sumbu bawah Yb = 15 cm
1
Ιx 
bh3
12
1
3

 20  30
12
 45000 cm 4
12
M.Ya
 lentur (atas) 
x
9  10 5  15
kg


300
2
3
cm
45  10
M.Yb
 lentur (bawah) 
Ιx
5
9  10  15
kg


300
2
3
cm
45  10
13
• Tegangan axial
– Yaitu tegangan yang ditimbulkan akibat beban
axial yang bekerja pada penampang balok
– Beban axial (P) dapat tekan atau tarik
P = gaya pada penampang balok
A = luas penampang balok (b x h)
14
P
b
HA
A
h

Tegangan axial pada balok
B
 ak  
P
A
kg
cm 2
15
P
HA
A

B
P kg
Tegangan axial pada balok  ak  
cm
A
2
16
Contoh tegangan aksial pada balok :
A=bxh
= 20 x 30 = 60 cm2
P
σ
A
 ak
P kg

2
cm
A
103 kg

2
cm
600
 1,67 kg
cm2
17
• Tegangan gabungan
– Yaitu gabungan dari Tegangan lentur +
tegangan axial
– Rumus
P Μ.Υ
σ 
A
Ι
18
 =  gabungan
P = gaya axial
A = luas penampang
M = momen lentur
Y = jarak sumbu ke serat atas / bawah
penampang
 = momen Inersia penampang
19
Dari contoh tersebut dapat dianalis sbb :
τa
τax  1,67 kg
-
30 cm
cm
a  τax
-
-
=
+
20 cm b  300 kg
τ ax
+
b  τax
cm2
20
• Tegangan geser ()
– Yaitu tegangan yang timbul akibat beban /
gaya lintang yang bekerja pada gelegar balok
dan terdistribusi sepanjang penam-pang
balok
– Rumus
LS kg
σ
2
cm
bΙ
L = gaya lintang (V)
S = statis momen
B = lebar penampang balok
 = momen inersia
21
Dari contoh sebelumnya dapat dianalisa tegang
geser yang terjadi sbb:
20 cm
τ1
30 cm
τ2
τ3
22
L  gaya lintang maksimum
b  15 cm
 VA
 6 ton  6000 kg
S  Statis Momen
1 3
Ix  bh
2
 45000 cm 4
1
1
b h h
2
4
 2250 cm3
23
LS
 
b.
6 10 3 x 225 x 10

15 x 45 x 1 0 3
 20 kg
cm 2
 1  0 karena S1  0
 3  0 karena S3  0
24
• Tegangan puntir ()
– Yaitu tegangan yang terjadi akibat gaya
peksentris sehingga menimbulkan Momen
terhadap sumbu x dan sumbu y, pada
penampang suatu balok.
– Rumus
P My . Xo Mx . Yo
σ dititik 0   

A
Ιy
Ιx
25
P
X
Mx
Ye
E
P
e
y
E
D
e
x
Y
My
C
Xe
B
luas A cm2
X
26
Gaya P terletak antara sumbu X dan Y
P dipindahkan kemtitik pusat sumbu X dan Y
Timbul momen Mx = P.ey dan My = P . ex
27
– Maka tegangan yang terjadi sbb :
P My . Xb Mx . Yb
Tegangan di B  σ B   

A
Ιy
Ιx
P My . Xc Mx . Yc
Tegangan di C  σ C   

A
Ιy
Ιx
P My . Xd Mx . Yd
Tegangan di D  σ D   

A
Ιy
Ιx
P My . Xe Mx . Ye
Tegangan di E  σ E   

A
Ιy
Ιx
28