Koreksi-Koreksi pada Pengolahan Data Geofisika

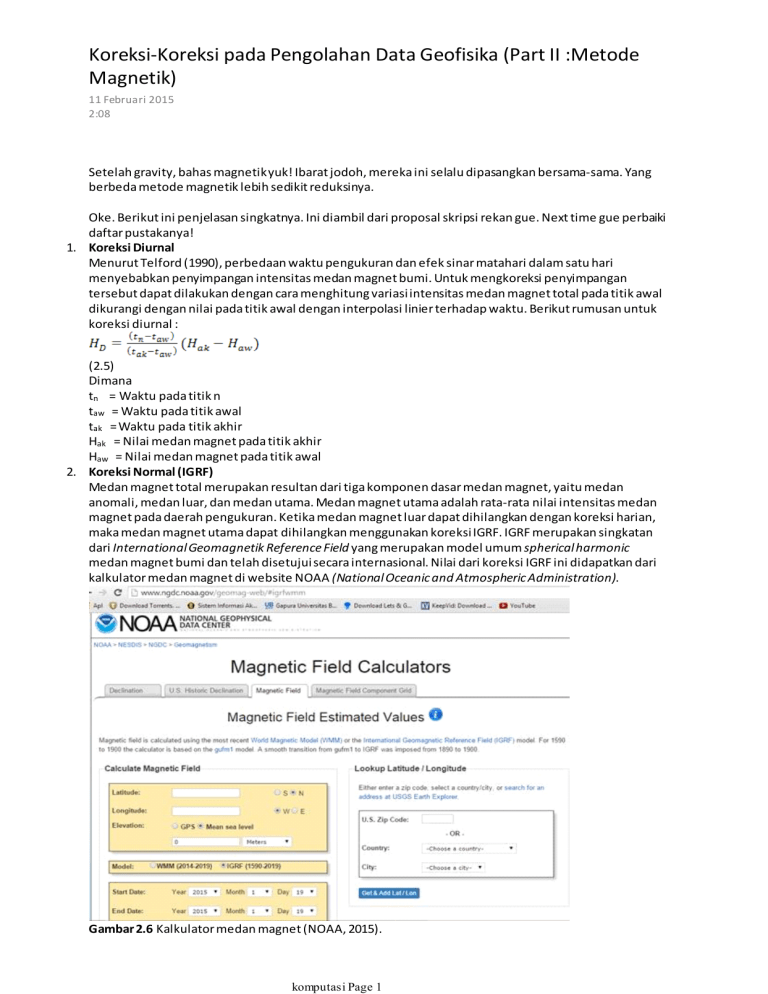
Koreksi-Koreksi pada Pengolahan Data Geofisika (Part II :Metode
Magnetik)
11 Februari 2015
2:08
Setelah gravity, bahas magnetik yuk! Ibarat jodoh, mereka ini selalu dipasangkan bersama-sama. Yang
berbeda metode magnetik lebih sedikit reduksinya.
Oke. Berikut ini penjelasan singkatnya. Ini diambil dari proposal skripsi rekan gue. Next time gue perbaiki
daftar pustakanya!
1. Koreksi Diurnal
Menurut Telford (1990), perbedaan waktu pengukuran dan efek sinar matahari dalam satu hari
menyebabkan penyimpangan intensitas medan magnet bumi. Untuk mengkoreksi penyimpangan
tersebut dapat dilakukan dengan cara menghitung variasi intensitas medan magnet total pada titik awal
dikurangi dengan nilai pada titik awal dengan interpolasi linier terhadap waktu. Berikut rumusan untuk
koreksi diurnal :
(2.5)
Dimana
tn = Waktu pada titik n
taw = Waktu pada titik awal
tak = Waktu pada titik akhir
Hak = Nilai medan magnet pada titik akhir
Haw = Nilai medan magnet pada titik awal
2. Koreksi Normal (IGRF)
Medan magnet total merupakan resultan dari tiga komponen dasar medan magnet, yaitu medan
anomali, medan luar, dan medan utama. Medan magnet utama adalah rata-rata nilai intensitas medan
magnet pada daerah pengukuran. Ketika medan magnet luar dapat dihilangkan dengan koreksi harian,
maka medan magnet utama dapat dihilangkan menggunakan koreksi IGRF. IGRF merupakan singkatan
dari International Geomagnetik Reference Field yang merupakan model umum spherical harmonic
medan magnet bumi dan telah disetujui secara internasional. Nilai dari koreksi IGRF ini didapatkan dari
kalkulator medan magnet di website NOAA (National Oceanic and Atmospheric Administration).
Gambar 2.6 Kalkulator medan magnet (NOAA, 2015).
Setelah didapatkan nilai dari koreksi IGRF, nilai anomali medan magnet dapat dihitung menggunakan
komputasi Page 1
Gambar 2.6 Kalkulator medan magnet (NOAA, 2015).
Setelah didapatkan nilai dari koreksi IGRF, nilai anomali medan magnet dapat dihitung menggunakan
perumusan berikut:
(2.6)
Dimana:
ΔH = Anomali medan magnet total
Hn = Medan magnet terukur
HD = Koreksi harian
HIGRF = Koreksi IGRF
3. Reduksi Bidang Datar
Data yang diperoleh dari pengukuran memiliki elevasi yang tidak teratur mengikuti topografi lokasi
pengambilan data menyebabkan terpengaruhnya permukaan yang termagnetisasi oleh medan magnet
bumi. Untuk memperkecil pengaruh dari topografi, dilakukan perataan kontur anomali medan magnetik
total ke dalam bidang datar. Bidang datar dalam hal ini merupakan topografi rata-rata di lokasi
pengambilan data. Menurut Blakely (1995), harga medan potensial titik (x,y) pada permukaan baru,
dikarenakan kontinuasi medan potensial U(x,y,zo) yang terukur pada level suface(permukaan rata
dengan zo = konstan) di uneven surface (permukaan tidak rata), dapat dirumuskan:
(2.7)
Konvergensi pada persamaan (2.7), secara empiris paling cepat jika zo diletakan pada pertengahan z(x,y).
Solusi persamaan tersebut dapat diperoleh menggunakan kawasan Fourier untuk turunan vertikal
medan terukur. Perumusan transformasi Fourier untuk turunan vertikal ke n medan potensial adalah :
(2.8)
Untuk transformasi dari uneven surface (permukaan tidak rata) ke level surface (permukaan rata), dapat
dirumuskan dengan pengaturan kembali persamaan (2.7) sehingga menjadi :
(2.9)
Gambar 2.7 Penggambaran permukaan tidak rata (Blakely,1995).
4. Kontinuasi ke Atas
Menurut Satiawan (2009), kontinuasi ke atas merupakan metode yang digunakan sebagai filter untuk
menghilangkan noise dari benda-benda dekat permukaan dan juga mengurangi efek dari anomali
dangkal. Metode ini menjadikan data seolah-olah diukur pada permukaan yang lebih atas dari suatu
level permukaan.
Menurut Blakely (1995), teorema Green merupakan konsep dasar dari kontinuasi ke atas. Untuk medan
potensial yang diukur pada level permukaan, kontinuasi yang paling sederhana adalah derivasi klasik
yang dijelaskan oleh Henderson (1970). Diasumsikan bahwa sumbu z pada koordinat Cartesian
mengarah ke bawah, medan potensial diukur pada permukaan datar dimana z = zo dan pada titik tunggal
P(x,y,zo-Δz) diatas permukaan datar dimana Δz>0. Pada gambar 2.8, permukaan S dengan radius α terdiri
atas dua tingkat yaitu permulaan datar dan hemisphere, sedangkan sumber berada pada z>zo. Ketika
, didapatkan persamaan sebagai berikut :
(2.10)
dimana
, dan Δz > 0.
komputasi Page 2
, dan Δz > 0.
Gambar 2.8 (a) Dalam batas S, dari perilaku R dapat diketahui fungsi harmonik tiap titiknya dalam
wilayah R. (b) Pada z=zo, terdapat medan potensial dan diharapkan berada pada titik P(x,y,zo-Δz) dimana
Δz > 0. Bidang horizontal dan setengah bola merupakan permukaan dari S dengan jari-jari α. Titik P
diproyeksikan terhadap bidang horizontal sehingga menghasilkan cerminan berupa P’ (Blakely, 1995).
(a) (b)
Gambar 2.9 (a) Kompilasi aeromagnetik Nevada Utara-Tengah dari Kucks dan Hildenbrand. (b) Anomali
magnetik total yang telah di kontinuasi ke atas sejauh 5 km (Blakely,1995).
5. Transformasi Pseudogravitasi
Transformasi pseudogravitasi baik digunakan untuk interpretasi anomali magnetik dikarenakan
transformasi tersebut merupakan analogi dari data gravitasi untuk benda magnet dengan massa jenis
komputasi Page 3
transformasi tersebut merupakan analogi dari data gravitasi untuk benda magnet dengan massa jenis
yang sebanding. Kesebandingan yang terjadi dalam transformasi ini bernilai 100kg/m3 per A/m, sehingga
1 A/m ≈ 102 gamma dan 1 gamma ≈ 1 kg/m3. Menurut Blakely (1995), benda termagnetisasi dan rapat
massa uniform yang menyebabkan potensial magnetik V dan potensial gravitasi U dapat direlasikan
menggunakan persamaan poison sebagai berikut (dengan asumsi M dan ρ adalah konstan) :
Dimana
ρ = Densitas
M = Intensitas magnetisasi
= Arah magnetisasi
= Komponen medan gravitasi saat arah magnetisasi
Hasil dari transformasi pseudogravitasi ini dapat digambarkan sebagaimana berikut :
Gambar 2.10Anomali magnetik dan setelah dilakukan transformasi pseudogravitasi (Blakely,1995).
Untuk mempermudah pengerjaan transformasi pseudogravitasi, dapat digunakan deret Fourier untuk
persamaan (2.11) dengan asumsi pada tiap titik, rasio
adalah konstan. Berikut transformasi Fourier dari persamaan (2.11) :
(2.12)
Untuk mendapatkan persamaan yang menghubungkan anomali medan magnet total dengan komponen
medan gravitasi, diperlukan kombinasi oleh persamaan (2.12) dengan persamaan berikut :
, (2.13)
sehingga menghasilkan persamaan
(2.14)
Anomali gravitasi pada komponen vertikal didapatkan dengan membagi kedua sisi dengan
. Dengan menyatakan anomali pseudogravitasi sebagai
, maka dapat diperoleh :
, (2.15)
dimana:
komputasi Page 4
(2.16)
Fungsi
merupakan filter untuk mentransformasi anomali medan magnet total pada permukaan horizontal ke
anomali pseudogravitasi (Blakely,1995).
(a) (b)
Gambar 2.11 (a) Kompilasi aeromagnetik Nevada Utara-Tengah dari Kucks dan Hildenbrand. (b) Anomali
pseudografitasi hasil transformasi dari gambar (a) (Blakely,1995).
6. Gradien Horizontal
Gradien Horizontal digunakan pada pengukuran gravitasi yang berfungsi untuk melokalisasi perubahan
densitas yang secara tiba-tiba kearah lateraldengan cara mengkarakterisasi anomali gravitasi
(Cordell,1979).Metode ini dapat dilakukan juga pada metode magnetik dengan mengubahnya terlebih
dahulu ke dalam anomali pseudogravitasi, dimana gradien horizontal yang curam menunjukkan bahwa
dalam magnetisasi terdapat perubahan lateral secara tiba-tiba (Cordell dan Grauch, 1985).
Menurut Blakely (1995), perumusan magnitude dari gradien horizontal anomali gravitasi adalah :
(2.17)
Gradien horizntal cenderung memiliki titik puncak di sekitar tepi sumber gravitasi (atau pseudogravitasi)
seperti yang ditunjukkan pada gambar 2.12.
komputasi Page 5
seperti yang ditunjukkan pada gambar 2.12.
Gambar 2.12 Anomali magnetik, anomali pseudogravitasi, dan gradien horizontal dengan sumber
batangan (Lesmana,2007).
Gambar 2.13 (a) Anomali total pada gambar 9(a) yang telah di transformasi pseudogravitasi dan gradien
horizontal. (b) Titik menunjukkan grafik maksimum dari gradiem horizontal yang secara otomatis
diketahui menggunakan metode Blakely dan Simpson (Blakely,1995).
Pasted from <file:///I:\PersiapanIUGC\Draft%20Proposal%20Tugas%20Akhir%20Andre.docx>
komputasi Page 6