BAB IV METODE ANALISIS RANGKAIAN 4.1 Analisis Arus Cabang

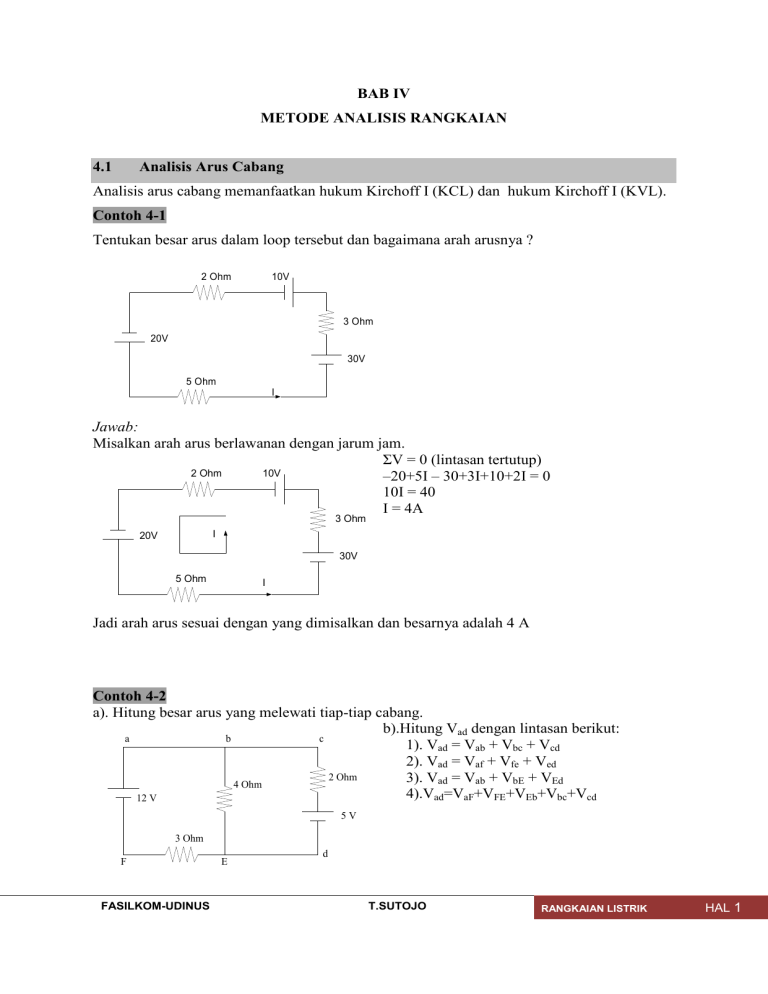
BAB IV
METODE ANALISIS RANGKAIAN
4.1
Analisis Arus Cabang
Analisis arus cabang memanfaatkan hukum Kirchoff I (KCL) dan hukum Kirchoff I (KVL).
Contoh 4-1
Tentukan besar arus dalam loop tersebut dan bagaimana arah arusnya ?
2 Ohm
10V
3 Ohm
20V
30V
5 Ohm
I
Jawab:
Misalkan arah arus berlawanan dengan jarum jam.
ΣV = 0 (lintasan tertutup)
2 Ohm
10V
–20+5I – 30+3I+10+2I = 0
10I = 40
I = 4A
3 Ohm
I
20V
30V
5 Ohm
I
Jadi arah arus sesuai dengan yang dimisalkan dan besarnya adalah 4 A
Contoh 4-2
a). Hitung besar arus yang melewati tiap-tiap cabang.
b).Hitung Vad dengan lintasan berikut:
a
b
c
1). Vad = Vab + Vbc + Vcd
2). Vad = Vaf + Vfe + Ved
2 Ohm
3). Vad = Vab + VbE + VEd
4 Ohm
4).Vad=VaF+VFE+VEb+Vbc+Vcd
12 V
5V
3 Ohm
F
FASILKOM-UDINUS
E
d
T.SUTOJO
RANGKAIAN LISTRIK
HAL 1
Jawab:
I
a
b
I2
c
I1
12 V
4 Ohm
1
2
Pilih titik cabang sembarang (misalnya Titik b)
kemudian tentukan arus yang Masuk dan arus
yang keluar titik cabang tersebut.
2 Ohm Tentukan arah putaran loop misalnya seperti
gambar disamping.
5V
3 Ohm
F
E
d
a). titik cabang B : I = I1 + I2.......(1)
Loop 1 : ΣV = 0
–12 + 4I1 + 3I = 0
–12 + 4I1 + 3 (I1 + I2) = 0
7I1 + 3I2 = 12.....................(2)
Loop 2 : ΣV = 0
–5 – 2I2 + 4I1 = 0
4I1 – 2I2 = 5 .........................(3)
Berdasarkan persamaan (1) dan nilai I1 dan I2 diperoleh :
I = I1 + I2  I = 1,5 + 0,5  I = 2 A
Pers (2) dan (3) diselesaikan diperoleh : I1 = 1,5 A dan I2 = 0,5 A
b). Untuk menentukan besar tegangan antara dua titik, lihat kembali tentang :”perjanjian
tanda beda potensial antara 2 titik.”
1). Vad = Vab + Vbc + Vcd
= 0 + 0 +2 (0,5) +5
= 6 Volt
2). Vad = Vaf + Vfe + Ved
= 12 + 3 (–2) + 0
= 6 Volt
3). Vad = Vab + Vbe + Ved
= 12 + 4 (1,5) + 0
= 6 Volt
4). Vad = Vaf + Vfe + Veb + Vbc + Vcd
= 12 + 3 (–2) + 4 ( –1,5) + 0 + 2 (0,5) + 5
= 6 Volt
Kesimpulan :
Besar tegangan antara dua titik sembarang tidak bergantung pada lintasan yang dipilih, jadi
untuk lintasan mana saja besar tegangan antara dua titik harus sama.
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 2
Contoh 4-3
1 Ohm
a
1 Ohm
b
a). Tentukan arus pada tiap-tiap cabang.
b). Hitung Vx
c). Hitung daya yang diserap tahanan 4Ω.
d). Hitung Va, Vb, Vc, Vd, Ve, Ve, bila Vf = 0
(ground)
c
(+)
2V
Vx =?
4 Ohm
2V
(-)
1 Ohm
4V
F
d
E
1 Ohm
Jawab:
a
I
1 Ohm
I1 1 Ohm
b
c
I2
2V
4 Ohm
1
2
1 Ohm
2V
4V
F
E
d
a). titik cabang b.
I = I1 + I2 ........(1)
Loop 1
I + 4I2 + I – 2 + 4 = 0
4I1 + 2I = –2
4I2 + 2 (I1+I2) = –2
2I1 + 6I2 = –2.........(2)
1 Ohm
Loop 2
4I2 – I1 – I1 + 4 – 2 = 0
–2I1 + 4I2 = –2..........(3)
Pers (2) dan (3) diselesaikan diperoleh :
I1 = 0,2Amp
I2 = 0,4Amp
Dan dari pers (1)
I = I1 +I2
= 0,2 – 0,4
= –0,2A
b). Vx = 4I2
= 4(–0,4)
= –1,6 Volt
c). Daya pada tahanan 4 Ω
P = I22 . R4Ω
= (-0,4)2 .4
= 0,64 Watt
d). Vaf = 2
FASILKOM-UDINUS
Vbf = – I.1+2
T.SUTOJO
RANGKAIAN LISTRIK
HAL 3
Va – Vf = 2
Va – 0 = 2
Va = 2 Volt
Vb – Vf = – (–0,2).1+2
Vb – 0 = 0,2+2
Vb = 2,2 Volt
Vcd = –2
Vcd – Vc = –2
Vd – 2 = –2
Vd = 0 Volt
Vef = 1 . I
Ve – Vf = 1 . (-0.2)
Ve – 0 = –0,2
Ve = –0,2 Volt
Contoh 4-4
Hitung besar arus i menggunakan análisis arus cabang pada rangkaian berikut.
Jawab:
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 4
Dari sini diperoleh nilai i = i1 = 1 A
4.2
Analisis Mesh (Arus Loop)
Metode analisis arus cabang sebaiknya digunakan untuk menyelesaikan rangkaian yang
mempunyai satu atau dua loop saja. Tetapi bila rangkaian yang diselesaikan mempunyai lebih
dari dua loop, pemakain analisis arus cabang mulai mengalami kesulitan, karena jumlah
persamaan yang terjadi banyak sekali, sebagai contoh bila dalam rangkaian ada 3 loop maka
jumlah persamaan yang ada sejumlah 7 buah. Karena itu digunakan cara lain untuk
menyelesaikannya. Berikut adalah metode yang digunakan untuk menyelesaikan rangkaian
yang mempunyai dua loop atau lebih.
Contoh 4-5
Tentukan besar arus yang lewat tiap-tiap cabang pada rangkaian berikut :
a
b
12
V
2
4
5V
3
F
FASILKOM-UDINUS
c
e
d
T.SUTOJO
RANGKAIAN LISTRIK
HAL 5
Jawab:
Tentukan arah arus pada tiap-tiap Loop. Misalnya seperti pada gambar berikut.
a
b
I1
12
V
c
I2
2
4
3
5V
F
d
e
Perhatikan cabang be yang dilalui arus I1, dan I2 dengan arah berlawanan.
* persamaan Loop I1
–12 + 3 I1 + 4(I1 – I2) = 0
7 I1 – 4 I2 = 12 ........................(1)
* persamaan Loop I2
5 + 2 I2 + 4 (I2 - I1) = 0
- 4 I1 + 6 I2 = –5 ......................(2)
Dari pers (1) dan pers (2) diperoleh I1 = 2A dan I2 = ½ A.
Arus yang lewat cabang be dicari dengan cara berikut :
b
Ibe
Ibe = I1 – I2 = 2 – ½ = 1,5 Amp.
I1
I2
e
Contoh 4-6
42 V
A
Tentukan besar arus yang lewat
tiap-tiap cabang!
B
3
3
4
E
6
D
6V
6
F
C
G
FASILKOM-UDINUS
4
H
T.SUTOJO
RANGKAIAN LISTRIK
HAL 6
Jawab:
42 V
A
B
Perhatikan cabang yang dilalui dua buah
arus, yaitu cabang :
DE : dilalui arus I1 dan I2
DC : dilalui arus I1 dan I3
DG : dilalui arus I2 dan I3
3
I1
3
6
4
D
E
C
I2
I3
6V
6
F
4
G
H
Loop I1
(3+3) I1 + 6 (I1 + I3) + 4 (I1 – I2) – 42 = 0
16 I1 – 4I2 + 6 I3 = 42 .............. ...................(1)
Loop I2
6I2 + 4 (I2 – I1) + 6 = 0
– 4I1 + 10I2 = –6 .............. ..........................(2)
Loop I3
4I3 + 6 (I3 + – I1) + 6 = 0
6I1 + 10I3 = –6 ................ ...........................(3)
diperoleh tiga persamaan yang akan diselesaikan dengan metode Determinan.
16 I1 – 4I2 + 6 I3 = 42 ................ ..............(1)
– 4I1 + 10I2 + 0.I3 = –6 ............ ..................(2)
6I1 + 0. I2 + 10I3 = –6 ............ ..................(3)
Determinan
16
4
6
I2
4 6
10 0
0 10
16
4
6
42 6
6 0
6 10
1080
1080
I1
42
6
6
4 6
10 0
0 10
I3
16
4
6
4
10
0
42
6
6
I2 =
I3
4320
3240
Menghitung I1 ; I2 ; I3
I1 =
I1
FASILKOM-UDINUS
I2 =
I2
T.SUTOJO
RANGKAIAN LISTRIK
HAL 7
=
4320
1080
=
= 4 A.
1080
1080
=
= 1 A.
3240
1080
= – 3 A.
Menghitung Arus pada cabang-cabang yang dilalui oleh dua arus :
Cabang DE :
Cabang DC:
I1
IDE
E
I2
IDE = I1 – I2
Cabang DG :
D
I1
D
D
IDC
C
I2
IDg
I3
I3
IDC = –I1 – I3
IDg = I2 – gI3
=4–1
= –4 + 3
=1–3
=3A
= –1 A
= –2 A
Contoh 4-7
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis mesh .
Jawab:
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 8
Pada contoh diatas, semua rangkaian hanya menggunakan pencatu berupa sumber
tegangan. bila pada rangkaian terdapat sumber arus, maka sumber arus yang ada
dijadikan supermesh, yaitu pemilihan lintasan diupayakan menghindari sumber arus,
karena pada sumber arus tidak diketahui besar tegangan terminalnya.
Contoh 4-8
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis mesh .
Jawab:
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 9
Contoh 4-9
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis mesh .
Jawab:
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 10
Dari sini diperoleh i = i3 = 2A
4.3
Analisis Node ( Simpul)
Sebelumnya perlu diketahui apa yang dimaksud dengan node. Node adalah titik pertemuan
dari dua atau lebih elemen rangkaian. Analisis node menggunakan Hukum Kirchoff I (KCL),
dimana jumlah aljabar arus yang masuk node sama dengan jumlah aljabar arus yang keluar
node. Sedangkan tegangan dipakai sebagai parameter yang belum diketahui. Analisis node
lebih mudah dikerjakan bila semua sumber pencatunya adalah sumber arus.
Langkah-langkah untuk mengerjakan analisis node, yaitu :
1. Tentukan node-node yang terdapat pada rangkaian
2. Pilih node referensi yaitu node yang dipakai sebagai potensial nol. Node ini dipilih
dari node yang mempunyai cabang paling banyak yang terhubung dengan node
tersebut.
3. Tentukan node voltage, yaitu tegangan antara node non referensi dan node referensi.
4. Anggap tegangan node yang sedang ditinjau lebih tinggi daripada tegangan node
manapun, sehingga arah arus keluar dari node tersebut positif.
5. Jika dalam rangkaian terdapat N node, maka jumlah node voltage adalah (N-1),
sehingga analisis ini menghasilkan (N-1) persamaan.
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 11
Contoh 4-10
Hitung besar arus i pada gambar berikut dengan menggunakan analisis node.
Jawab:
- Tentukan node-node yang ada pada rangkaian
- Tentukan node referensinya
- Tentukan node voltage
Berdasarkan Gambar diatas, jumlah N = 3.
Maka jumlah persamaan ada : 3 – 1 = 2
Lihat node V1 (KCL):
i1
i2
i1
i2
7
4
3
V1 V3 V1 V2
3
4
8
V1 0 V1 V2
3
4
8
3V1 V2
24.........(1)
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 12
Lihat node V2 (KCL):
i1
i2
7
V2 V1 V2 V3
7
8
12
V2 V1 V2 0
7
8
12
3V1 5V2 168.........(2)
Berdasarkan persamaan (1) dan (2) diperoleh, V1 = 4 volt dan V2 = 36 volt.
i
V1 V3
4
4 0
4
1A
Contoh 4-11
Tentukan nilai tegangan v pada rangkaian berikut dengan menggunakan analisis node.
Jawab :
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 13
Lihat node Va (KCL):
Va
0 Va Vb
9
8
16
3Va Vb 144.........(1)
Lihat node Vb (KCL):
Vb 0 Vb Va
3
12
16
3Va 7Vb 144.........(2)
Berdasarkan persamaan (1) dan (2) diperoleh, Va = 64 volt dan Vb = 48 volt.
Berdasarkan gambar rangkaian diatas, v = Va = 64 volt
Contoh 4-12
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis node.
Jawab :
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 14
Lihat node Va (KCL):
Va 0 Va Vb
12 6i
10
40
Va 0 Va Vb
V
12 6 a
10
40
10
19Va Vb 480.................(1)
Lihat node Vb (KCL):
Vb 0 Vb Va
6i 2
20
40
Vb Vb Va
V
6 a 2
20
40
10
23Va 3Vb 80.................(2)
Berdasarkan persamaan (1) dan (2) diperoleh, Va = 40 volt
i
Va
10
40
10
4A
Pada contoh diatas, semua rangkaian hanya menggunakan pencatu berupa sumber arus.
bila pada rangkaian terdapat sumber tegangan, maka sumber tegangan yang ada
dijadikan supernode, yaitu sumber tegangan dianggap sebagai satu node.
Contoh 4-13
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis node.
Jawab :
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 15
Perhatikan bahwa sumber tegangan 20V dianggap sebagai super node (satu node)
Lihat node V (KCL):
V 0 V 20
1
10
10
V 15volt
20 V 20 15
i
10
10
0,5 A
Contoh 4-14
Tentukan besar arus v pada rangkaian berikut dengan menggunakan analisis node.
Jawab :
Lihat node Va (KCL):
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 16
Va 0 Va 16
12
8
Va 24volt
v Va 16
3
24 16 8volt
Contoh 4-15
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis node.
Jawab :
Lihat node Va (KCL):
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 17
Contoh 4-16
Tentukan besar arus vx pada rangkaian berikut dengan menggunakan analisis node.
Jawab:
Lihat node 1 (KCL):
v1 v1 v1 v 2 v x
2 1
8
4
dim ana v x v 2
0
v1 v1 v1 v 2 v 2
0
2 1
8
4
13v1 v 2 0........................(1)
Lihat node 2 (KCL):
vx
v2
14
8
4
4
v 2 v1 v 2
v
14 2
8
4
4
v1 v 2 112...........(2)
v2
v1
Berdasarkan persamaan (1) dan (2) diperoleh, v1 = −8 volt , dan v2 = 104 volt
Sehingga, vx = v2 = 104 volt
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 18
SOAL-SOAL LATIHAN
1.
Hitung besar arus i pada rangkaian berikut dengan menggunakan analisis arus cabang.
2.
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis node.
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 19
3.
Tentukan besar tegangan v pada rangkaian berikut dengan menggunakan analisis
node.
4.
Tentukan besar arus i pada rangkaian berikut dengan menggunakan super node
5.
Tentukan besar tegangan v pada rangkaian berikut dengan menggunakan super node
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 20
6.
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis mesh
7.
Tentukan besar tegangan v pada rangkaian berikut dengan menggunakan analisis
mesh
8.
Tentukan besar arus i pada rangkaian berikut dengan menggunakan analisis
supermesh
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 21
9.
Tentukan besar tegangan v pada rangkaian berikut dengan menggunakan analisis
supermesh
10.
Tentukan besar arus i pada rangkaian berikut
FASILKOM-UDINUS
T.SUTOJO
RANGKAIAN LISTRIK
HAL 22