Latihan 1

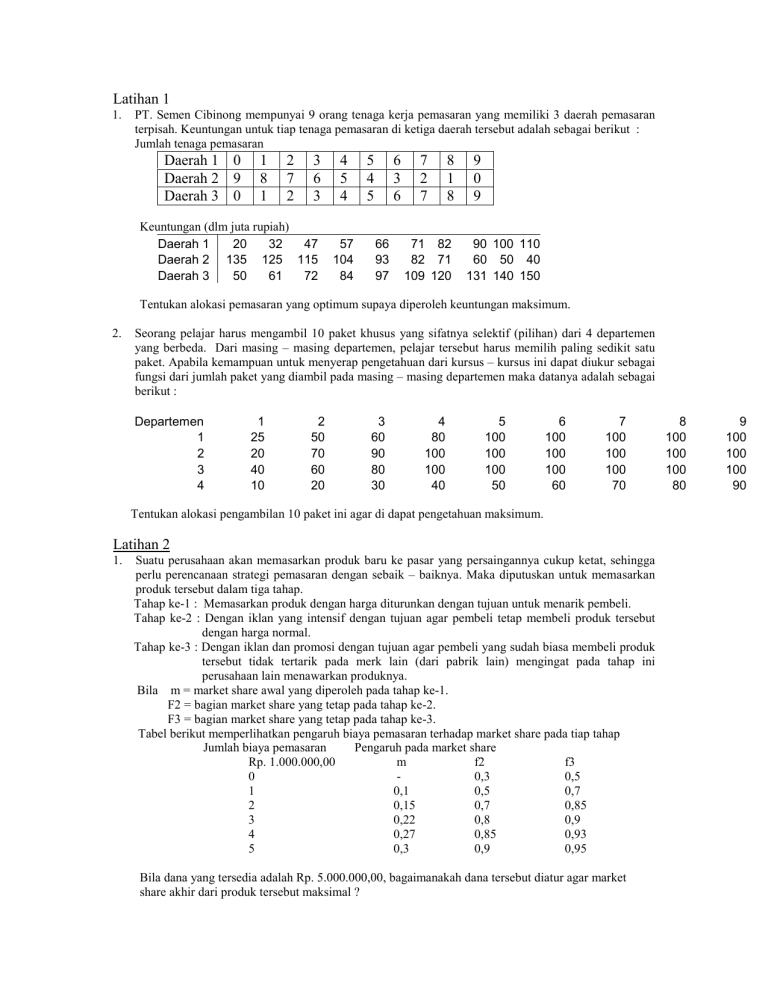
Latihan 1
1.
PT. Semen Cibinong mempunyai 9 orang tenaga kerja pemasaran yang memiliki 3 daerah pemasaran
terpisah. Keuntungan untuk tiap tenaga pemasaran di ketiga daerah tersebut adalah sebagai berikut :
Jumlah tenaga pemasaran
Daerah 1 0
Daerah 2 9
Daerah 3 0
1
8
1
2
7
2
3
6
3
Keuntungan (dlm juta rupiah)
Daerah 1
20
32
47
Daerah 2 135 125 115
Daerah 3
50
61
72
4
5
4
57
104
84
5
4
5
6
3
6
66
93
97
7
2
7
8
1
8
71 82
82 71
109 120
9
0
9
90 100 110
60 50 40
131 140 150
Tentukan alokasi pemasaran yang optimum supaya diperoleh keuntungan maksimum.
2.
Seorang pelajar harus mengambil 10 paket khusus yang sifatnya selektif (pilihan) dari 4 departemen
yang berbeda. Dari masing – masing departemen, pelajar tersebut harus memilih paling sedikit satu
paket. Apabila kemampuan untuk menyerap pengetahuan dari kursus – kursus ini dapat diukur sebagai
fungsi dari jumlah paket yang diambil pada masing – masing departemen maka datanya adalah sebagai
berikut :
Departemen
1
2
3
4
1
25
20
40
10
2
50
70
60
20
3
60
90
80
30
4
80
100
100
40
5
100
100
100
50
6
100
100
100
60
7
100
100
100
70
Tentukan alokasi pengambilan 10 paket ini agar di dapat pengetahuan maksimum.
Latihan 2
1.
Suatu perusahaan akan memasarkan produk baru ke pasar yang persaingannya cukup ketat, sehingga
perlu perencanaan strategi pemasaran dengan sebaik – baiknya. Maka diputuskan untuk memasarkan
produk tersebut dalam tiga tahap.
Tahap ke-1 : Memasarkan produk dengan harga diturunkan dengan tujuan untuk menarik pembeli.
Tahap ke-2 : Dengan iklan yang intensif dengan tujuan agar pembeli tetap membeli produk tersebut
dengan harga normal.
Tahap ke-3 : Dengan iklan dan promosi dengan tujuan agar pembeli yang sudah biasa membeli produk
tersebut tidak tertarik pada merk lain (dari pabrik lain) mengingat pada tahap ini
perusahaan lain menawarkan produknya.
Bila m = market share awal yang diperoleh pada tahap ke-1.
F2 = bagian market share yang tetap pada tahap ke-2.
F3 = bagian market share yang tetap pada tahap ke-3.
Tabel berikut memperlihatkan pengaruh biaya pemasaran terhadap market share pada tiap tahap
Jumlah biaya pemasaran
Pengaruh pada market share
Rp. 1.000.000,00
m
f2
f3
0
0,3
0,5
1
0,1
0,5
0,7
2
0,15
0,7
0,85
3
0,22
0,8
0,9
4
0,27
0,85
0,93
5
0,3
0,9
0,95
Bila dana yang tersedia adalah Rp. 5.000.000,00, bagaimanakah dana tersebut diatur agar market
share akhir dari produk tersebut maksimal ?
8
100
100
100
80
9
100
100
100
90
Latihan 3
1.
Selesaikanlah masalah Linier Programming berikut dengan Dinamik Programming
Max : Z = 8X1 + 7X2
Kendala :
2X1 + X2 ≤ 8
5X1 + 2X2 ≤ 15
a. X1 dan X2 non negatif integer.
b. X1 dan X2 non negatif real.
2.
Selesaikan masalah non linier berikut dengan Dinamik Programming :
Max : Z = 7X12 + 6X1 +5X22
Kendala :
X1 + 2X1 ≤ 10
X1 - 3X2 ≤ 9
X1, X2 ≥ 0
Gunakan programma dinamik maju.
3. Seseorang akan menginvestasikan uang sebesar Rp. 10 juta selama 3 tahun. Ada dua alternatif investasi
yang bisa dipilih yaitu A dan B.
Alternatif A : Bila diinvestasikan Rp. 10 juta pada awal tahun, maka pada akhir tahun mungkin akan
rugi Rp. 10 juta atau untung Rp. 10 juta.
Alternatif B : Bila diinvestasikan Rp. 10 juta pada awal tahun, maka pada akhir tahun mungkin jumlah
uangnya tetap atau mendapat untung Rp. 10 juta.
Probabilitas kejadian ini adalah :
Alternatif Jumlah uang pada akhir tahun Probabilitas
A
0 juta
0.4
20 juta
0.6
B
10 juta
0.9
20 juta
0.1
Tiap tahun hanya boleh 1 kali investasi masing – masing Rp.10 juta. Bagaimanakah kebijakan investasi
yang baik agar dalam 3 tahun di dapat jumlah uang maksimal !
Latihan 4
1. Untuk setiap matriks pembayaran berikut, tentukan strategi optimal untuk tiap pemain. Setelah
dilakukan aturan dominansi.
a.
Pemain 2
1
2
3
1
-3
1
1
2
1
2
0
Pemain 1
3
2
1
-2
b.
Pemain 2
1
1
2
0
1
2
3
2
2
-3
3
3
0
-2
--1
Pemain 1
c.
Pemain 2
1
-3
1
1
1
2
3
2
1
2
0
3
2
1
-2
4
1
2
3
Pemain 1
2. Tentukan titik sadel dari permainan yang memiliki matriks pembayaran sebagai berikut :
a. Pemain 2
1
2
3
1
1
-2
3
2
-1
-0
1
3
1
3
2
2
-3
-2
-1
3
-2
-1
2
Pemain 1
b.
Pemain 2
1
2
3
1
3
-4
1
4
-4
1
0
Pemain 1
3. Dua buah tim renang kota bebek dan kota angsa akan mengadakan pertandingan. Tiap tim punya
perenang andalan (Donald untuk kota Bebek dan Gus untuk kota Angsa) yang dapat berenang dengan
sangat baik untuk 100 yard gaya kupu – kupu, gaya punggung dan gaya dada. Tetapi terdapat peraturan
yang melarang menurunkan mereka dalam pertandingan untuk lebih dari 2 gaya. Karena itu pelatih
perlu mengatur strategi untuk menggunakan mereka secara maksimum. Pada tiap gaya, tiap tim akan
turun dengan 3 perenang. Diberikan tabel waktu terbaik yang dicapai oleh para perenang ini pada
pertandingan yang lalu sebagai berikut :
Kota Bebek
Gaya
1
2
Donald
Kupu – kupu
1:01.6
59.1
57.5
Punggung
1:06.8 1:05.6
1:03.3
Dada
1:13.9 1:12.5
1:04.7
Kota Angsa
Gus
1
57.5
1:03.2
1:02.6
1:04.9
1:06.1
1:15.3
2
59.8
1:04.1
1:11.8
Jika Donald/Gus tidak diturunkan pada gaya tertentu, maka penggantinya (perenang 3) memiliki waktu
tempuh yang lebih lambat dari perenang 1 dan 2 di atas.
Juara I mendapat poin 5
Juara II mendapat poin 3
Juara III mendapat poin 1
Tidak juara mendapat poin 0
Tentukan matriks permainannya !!!!!
Latihan 5
1. Untuk tiap matriks pembayaran berikut jelaskan dengan metode grafik/simplex dan tentukkan nilai
optimumnya :
a.
1
2
3
1
4
3
1
2
0
1
2
b.
1
2
3
4
1
1
0
3
-3
2
-1
4
-2
6
3
3
1
5
-2
2. Terdapat sebuah permainan yang dimainkan oleh dua orang. Tiap – tiap pemain mula – mula punya 3
koin :
1 berwarna merah
1 berwarna putih
1 berwarna biru
Tiap koin hanya dapat digunakan 1 kali.
Permainan dimulai dengan : Tiap pemain meletakkan 1 koin di atas meja. Kedua pemain ini lalu
membuka koinnya dan menentukan pembayaran untuk pemenang. Jika kedua pemain menaruh koin
dengan warna sama maka permainan dianggap imbang, lainnya mengikuti tabel sebagai berikut :
Koin yang menang
Merah > putih
Putih > biru
Biru > merah
Kedua warna sama
Pembayaran
50
40
30
0
Selanjutnya tiap pemain memilih lagi 1 dari 2 koinnya yang tersisa dan mengulangi prosedur permainan
hingga koin terakhir dimainkan.
Formulasikan masalah ini dalam permainan berjumlah 2 orang dengan total nilai permainan nol.
Latihan 6
1. Dua orang mahasiswa, kontrak rumah di Siwalankerto dan hendak membagi pekerjaan rumah yang
terdiri dari ke pasar, memasak, mencuci dan menyetrika secara efisien, sehingga waktu yang
dibutuhkan minimum. Efisiensi dari pekerjaab mereka masing – masing adalah :
Jam / minggu
Ke pasarmemasak
mencuci menyetrika
A
4.5
7.8
3.6
2.9
B
4.9
7.2
4.3
3.1
Buatlah model BIP dari masalah ini.
2. Formulasikan masalah ini ke dalam MIP
Min Z = f1(X1) + f2(X2)
Kendala :
1. salah satu dari X1 ≥ 3 atau X2 ≥ 3.
2. sekurang-kurangnya salah satu dari kendala – kendala ini terpenuhi :
2X1 + X2 ≥ 7
X 1 + X2 ≥ 5
X1 + 2X2 ≥ 7
3. X1 – X2  = 0 atau 3 atau 6.
4. X1 ≥ 0, X2 ≥ 0
Dimana f1(X1) =  7 + 5X1 jika X1 > 0
0
jika X1 = 0
f2(X2) =  5 + 6X2 jika X2 > 0
0
jika X2 = 0
3. Sebuah kotamadya dengan 6 kecamatan bermaksud mendirikan pusat pemadam kebakaran (PPK) untuk
melindungi masyarakatnya.
Walikota yang bersangkutan menghendaki agar jumlah PPK yang dibangun adalah seminimum
mungkin, tetapi sedikitnya harus ada 1 PPK dalam jarak tempuh 15 menit dari satu kecamatan ke
kecamatan lainnya. Data waktu tempuh (dalam menit ).
Ke
1
2
3
4
5
6
10
0
25
35
20
10
20
25
0
15
30
20
30
35
15
0
15
25
30
20
30
15
0
14
20
10
20
25
14
0
Dari
1
2
3
4
5
6
0
10
10
30
30
20
4. (Pilihan)
Buatlah program AMPL untuk masalah TSP berikut
B
6
3
D
5
3
A
F
4
C
Petunjuk :
1.
2.
2
3
E
Buat order set : set vertex ordered;
Buat pairwise set : set edge within vertex cross vertex;