Alat-alat Optik (1) Mata – Lup

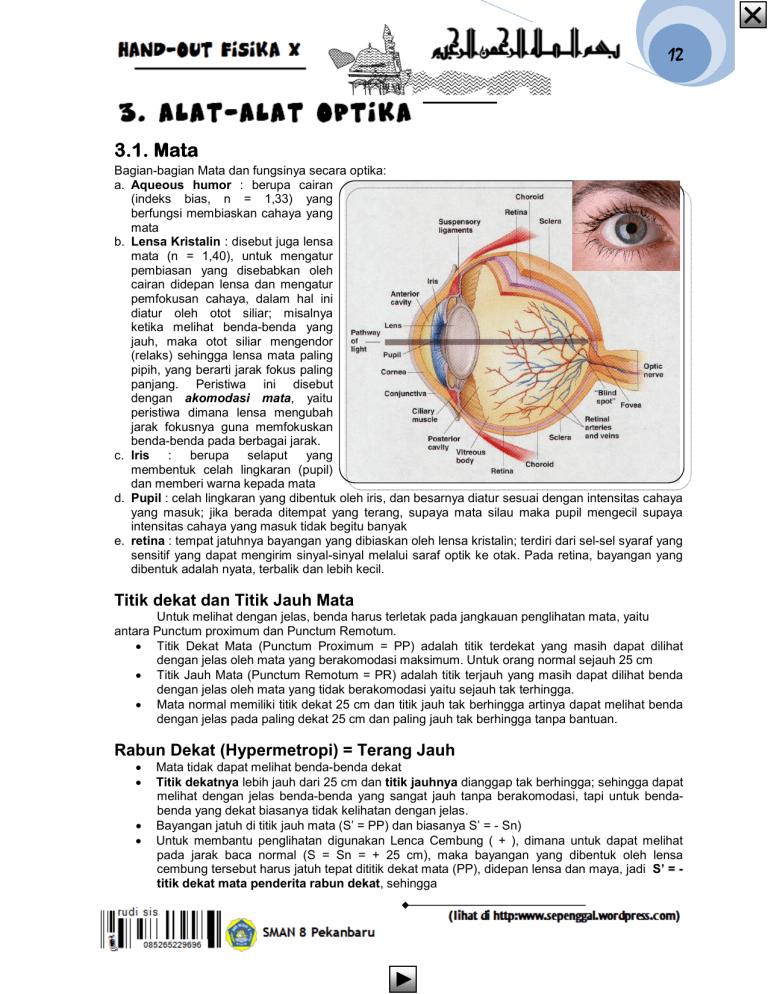
12
3.1. Mata
Bagian-bagian Mata dan fungsinya secara optika:
a. Aqueous humor : berupa cairan
(indeks bias, n = 1,33) yang
berfungsi membiaskan cahaya yang
mata
b. Lensa Kristalin : disebut juga lensa
mata (n = 1,40), untuk mengatur
pembiasan yang disebabkan oleh
cairan didepan lensa dan mengatur
pemfokusan cahaya, dalam hal ini
diatur oleh otot siliar; misalnya
ketika melihat benda-benda yang
jauh, maka otot siliar mengendor
(relaks) sehingga lensa mata paling
pipih, yang berarti jarak fokus paling
panjang. Peristiwa ini disebut
dengan akomodasi mata, yaitu
peristiwa dimana lensa mengubah
jarak fokusnya guna memfokuskan
benda-benda pada berbagai jarak.
c. Iris : berupa selaput yang
membentuk celah lingkaran (pupil)
dan memberi warna kepada mata
d. Pupil : celah lingkaran yang dibentuk oleh iris, dan besarnya diatur sesuai dengan intensitas cahaya
yang masuk; jika berada ditempat yang terang, supaya mata silau maka pupil mengecil supaya
intensitas cahaya yang masuk tidak begitu banyak
e. retina : tempat jatuhnya bayangan yang dibiaskan oleh lensa kristalin; terdiri dari sel-sel syaraf yang
sensitif yang dapat mengirim sinyal-sinyal melalui saraf optik ke otak. Pada retina, bayangan yang
dibentuk adalah nyata, terbalik dan lebih kecil.
Titik dekat dan Titik Jauh Mata
Untuk melihat dengan jelas, benda harus terletak pada jangkauan penglihatan mata, yaitu
antara Punctum proximum dan Punctum Remotum.
• Titik Dekat Mata (Punctum Proximum = PP) adalah titik terdekat yang masih dapat dilihat
dengan jelas oleh mata yang berakomodasi maksimum. Untuk orang normal sejauh 25 cm
• Titik Jauh Mata (Punctum Remotum = PR) adalah titik terjauh yang masih dapat dilihat benda
dengan jelas oleh mata yang tidak berakomodasi yaitu sejauh tak terhingga.
• Mata normal memiliki titik dekat 25 cm dan titik jauh tak berhingga artinya dapat melihat benda
dengan jelas pada paling dekat 25 cm dan paling jauh tak berhingga tanpa bantuan.
Rabun Dekat (Hypermetropi) = Terang Jauh
•
•
•
•
Mata tidak dapat melihat benda-benda dekat
Titik dekatnya lebih jauh dari 25 cm dan titik jauhnya dianggap tak berhingga; sehingga dapat
melihat dengan jelas benda-benda yang sangat jauh tanpa berakomodasi, tapi untuk bendabenda yang dekat biasanya tidak kelihatan dengan jelas.
Bayangan jatuh di titik jauh mata (S’ = PP) dan biasanya S’ = - Sn)
Untuk membantu penglihatan digunakan Lenca Cembung ( + ), dimana untuk dapat melihat
pada jarak baca normal (S = Sn = + 25 cm), maka bayangan yang dibentuk oleh lensa
cembung tersebut harus jatuh tepat dititik dekat mata (PP), didepan lensa dan maya, jadi S’ = titik dekat mata penderita rabun dekat, sehingga
u
13
Lensa
cembung
Benda
dekat
Benda
dekat
Sn
PP = S’
Rabun Jauh (Myopi) = Terang Dekat
•
•
•
•
•
Mata tidak dapat melihat benda-benda jauh
Titik dekat mata (PP) lebih dekat tak hingga, dan bayangan jatuh di depan retina
Untuk membantu penglihatan digunakan kacamata negatif
Untuk membantu penglihatan digunakan Lensa cekung ( - ), dimana agar mata dapat melihat
dengan normal benda yang jauh (S = ~), maka bayangan yang dibentuk oleh lensa cekung
tersebut harus jatuh dititik jauh mata (S’ = - PR) , didepan lensa dan maya
Atau kekuatan kacamata yang harus digunakan adalah
F=-
1
100
dimana PM = −
PR
PM
(3.1)
Lensa
cekung
Sinar
sejajar
dari
benda
jauh
PR = S’
S=~
u
14
Mata Tua (Presbiopi)
Cacat mata karena berkurang daya akomodasi karena lanjut usia. Titik dekat lebih besar dari
25 cm dan titik jauh pada jarak tertentu. Sehingga penderita presbiopi tidak dapat melihat benda
dengan jelas dan juga tidak dapat membaca pada jarak baca normal. Dapat ditolong dengan kaca mata
bifokal (lensa rangkap)
Mata Astigmatisma
Cacat mata yang tidak dapat melihat garis vertikal dan horizontal bersama-sama, ditolong
dengan kaca mata silindris. Penyebabnya adalah karena kornea mata yang tidak berbentuk sferik,
artinya salah satu bidang lebih melengkung dibanding bidang lain, sehingga biasanya sinar-sinar pada
bidang vertikal difokuskan lebih pendek daripada sinar-sinar pada bidang horisontal.
Sekedar Games
Apakah dua garis horisontal tersebut sejajar?
u
Manakah yang lebih tua? Kiri atau kanan?
15
39. Seorang pelajar memakai kacamata berukuran – ¾ dioptri untuk sebelah kanan dan – ¼ dioptri
untuk sebelah kiri. Jika pelajar tersebut tidak menggunakan kacamata, berapa jarak terjauh yang
dapat terlihat dengan jelas oleh kedua matanya?
40. Pada saat membaca, jarak terdekat yang dapat dilihat seorang kakek rabun dekat adalah 40 cm.
Hitunglah kekuatan lensa kacamat yang diperlukan!
41. Seseorang yang berpenglihatan jauh dapat membaca dengan jelas tanpa kacamata pada jarak
tidak kurang dari 75 cm. Ia menggunakan kacamata yang memiliki kuat lensa 2,5 dioptri. Berapa
titik dekat setelah ia memakai kacamata?
42. Seseorang memakai kacamata – ½ dioptri agar ia dapat melihat benda yang sangat jauh dengan
jelas. Jika ia melepas kacamatanya, berapakah jarak paling jauh yang masih dapat dilihatnya
dengan jelas?
43. Seorang bermata miopi titik jauhnya 4 m, melihat bintang tak berakomodasi. Hitung berapa
kekuatan kacamata yang diperlukan
44. Seseorang yang berpenglihatan dekat tidak dapat melihat dengan jelas benda yang berjarak lebih
dari 60 cm diukur dari mata. Berapa kuat lensa kacamata yang memungkinkan ia dapat melihat
dengan jelas
45. Seseorang yang berpenglihatan jauh tidak dapat melihat dengan jelas benda yang berjarak lebih
dekat dari 75 cm diukur dari mata. Berapa kuat lensa kacamata yang diperlukan agar ia dapat
membaca dengan jelas pada jarak 25 cm
46. Seorang tua bermata presbiopi yang memiliki titik dekat 40 cm dan membaca buku dengan
memakai kacamata dengan jarak baca 25 cm, ternyata orang itu berakomodasi maksimum. Hitung
kekuatan kacamata yang diperlukan
47. Berdasarkan pemeriksaan, seseorang dianjurkan menukar lensa kacamatanya dari 0,80 dioptri
menjadi 1,25 dioptri. Berapa jauhkah pergeseran titik dekat mata orang tersebut?
48. Seseorang yang menggunakan kacamata 3 dioptri dapat melihat dengan jelas pada jarak 25 cm
didepan matanya. Jika ia ingin melihat benda dengan jelas tanpa kacamata, hitunglah jarak paling
dekat benda ke matanya!
3.2. Lup
Digunakan untuk memperbesar sudut pandang. Untuk mendapatkan perbesaran maksimum
benda diletakkan diruang I (antara titik pusat optik dengan fokus f) sehingga bayangan di ruang IV
didepan lensa, maya dan tegak
Perbesaran Sudut (anguler)
Perbesaran Sudut (M) yaitu perbandingan antara sudut penglihatan dengan lup (β) dan tanpa
lup (α)
M=
β
Sn
=
α
S
(3.2)
Ukuran anguler berperan dalam hal memberi kesan seberapa besar benda yang dilihat mata.
Sebagai contoh: perhatikan sebuah mobil yang bergerak mendekati kita; ketika masih jauh mobil
tersebut kelihatan kecil, tetapi semakin dekat dengan kita, maka mobil tersebut kelihatan menjadi besar.
Padahal ukuran mobil yang kita lihat sebenarnya adalah tetap.
u
16
Sebagai contoh perhatikan diagram benda berikut:
A
B
C
α1 α2
0
0
α3
0
0
OA, OB dan OC adalah benda yang sama tingginya,
namun karena berbeda jaraknya, maka sudut
penglihatannya menjadi berbeda, OA yang paling jauh
memiliki sudut penglihatan yang kecil dibandingkan OB
dan OC, (α1 < α2 < α3), dan bayangan yang dibentuk
diretina, OC yang paling dekat terlihat lebih tinggi,
Jadi OC1 > OB1 > OA1
A1
B1
C1
Mata berakomodasi pada jarak x
Untuk mata berakomodasi pada jarak x, artinya bayangan yang dibentuk oleh lensa jatuh pada
jarak x di depan mata (S’ = - x), sehingga perbesaran lup adalah
M=
Sn
Sn
+
f
x
Contoh 3.3
(3.3)
Petunj
etunjuk:
uk:
Seorang tukang jam menggunakan
lup yang berkekuatan 8 dioptri,
dimanakah letak
benda dan
perbesaran anguler yang diperoleh
jika mata tukang jam tersebut
berakomodasi pada jarak 50 cm.
Hitung terlebih dahulu fokus lensa
Didapat fokus lensa = 12,5 cm (jawaban)
Mata berakomodasi pada jarak 50 cm, maka x = 50 cm,
jarak bayangan S’ = - x = - 50 cm.
Dengan menggunakan persamaan lensa tipis, maka
diperoleh letak benda, S = 10 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3.3):
Sn
Sn
25
25
+
M=
+
M=
12,5
50
f
x
M = 2,5 (jawaban)
Mata Berakomodasi Maksimum
Untuk mata berakomodasi maksimum, bayangan yang dihasilkan lup harus terletak dititik dekat
mata. Sehingga bayangannya, S’ = - Sn, sehingga persamaan (3.) menghasilkan perbesaran Lup yaitu:
M=
Sn
+1
f
u
(3.4)
17
Mata Tak Berakomodasi
Untuk mata tidak berakomodasi (supaya mata tidak cepat lelah), maka benda (S) diletakkan
pada titik fokus lensa (lup), sehingga bayangan akan diperbesar dan jatuh di jauh tak berhingga (S1 = ~,
S = f)
Sn
Perbesaran Lup adalah
M=
(3.5)
f
Mata berakomodasi pada jarak x dan Lup tidak menempel pada mata
Untuk mata berakomodasi pada jarak x, dan mata mempunyai jarak d
perbesaran yang dihasilkan adalah
M=
Sn
Sn d Sn
+
f
x
fx
Contoh 3.4
dari lup, maka
(3.6)
Petunj
etunjuk:
uk:
Seorang tukang jam menggunakan
lup yang berkekuatan 8 dioptri,
dimanakah letak
benda dan
perbesaran anguler yang diperoleh
jika mata tukang jam tersebut
a. berakomodasi maksimum
b. tidak berakomodasi
(titik jauh dekat pengamat 25 cm)
Contoh 3.5
3.5
Hitung terlebih dahulu fokus lensa
Didapat fokus lensa = 12,5 cm (jawaban)
a. Mata berakomodasi maksimum,
maka S’ = - Sn = - 25 cm
Dengan menggunakan persamaan lensa tipis, maka
diperoleh letak benda, S = 25/3 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3.4):
Sn
25
+1M=
+1
M=
12,5
f
M = 3 (jawaban)
b. Mata tidak berakomodasi
Titik jauh pengamat ada di tak berhingga, maka benda
terletak didepan lensa dan di titik fokus, maka
S = f = 12,5 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3.5)
Sn
25
M=
M=
12,5
f
M = 2 (jawaban)
Petunj
etunjuk:
uk:
Sebuah lup berkekuatan 20 dioptri,
dimanakah letak
benda dan
perbesaran anguler yang diperoleh
jika pengamat yang menggunakan
lup tersebut tidak berakomodasi,
dan mempunyai titik dekat 30 cm
dan titik jauhnya 2 meter.
Hitung terlebih dahulu fokus lensa
Didapat fokus lensa = 5,0 cm (jawaban)
Karena titik jauh pengamat 2,00 m bukan di titik jauh tak
hingga, maka bayangan lensa harus terletak di depan lensa
pada jarak titik jauh pengamat, jadi S’ = - 200 cm.
Dengan menggunakan persamaan lensa tipis, maka
diperoleh letak benda, S = 200/41 cm (jawaban)
Perbesaran lup dapat menggunakan persamaan (3.2)
M=
Sn
30
M=
S
200/41
M = 6,15 (jawaban)
u
18
Latihan 6.
49. Seorang bermata normal memakai lup yang kekuatannya 20 dioptri. Hitung perbesaran
sudutnya jika:
a. mata berakomodasi maksimum
b. mata tak berakomodasi
50. Seseorang bermata normal mengamati benda dengan sebuah lup yang kuatnya 18 dioptri.
Berapakah perbesaran sudutnya jika:
a. mata berakomodasi maksimum
b. mata tidak berakomodasi
c. mata berakomodasi pada jarak 80 cm
d. mata berakomodasi pada jarak 80 cm tetapi mata menjauh sebesar 2 cm
51. Seseorang menggunakan lup yang kekuatannya 4 dioptri. Sebuah benda yang tingginya 2
cm diamati oleh orang tersebut. Berapakah tinggi bayangan yang dilihat jika
a. benda terletak pada jarak 24 cm
b. benda terletak pada jarak 25 cm
52. Sebuah benda diletakkan didepan lensa cembung sejauh 5,00 cm dan terbentuk bayangan
nyata pada jarak 20,0 cm dari lensa. Jika lensa digunakan sebagai lup, tentukanlah
perbesaran anguler lup, untuk
a. Mata berakomodasi pada jarak 40 cm
b. Mata tidak berakomodasi
53. Seseorang memiliki titik dekat 27 cm, melihat bayangan sebuah benda dengan lup
diperbesar 10 kali saat ia melihatnya dengan berakomodasi sekuat-sekuatnya.
a. Tentukan fokus lup dan kekuatanya
b. Kemana benda harus digeser dan berapa jauhnya, agar perbesaran sudutnya menjadi
9
9
kali
14
54. Dua orang eR dan Sis memiliki kacamata masing-masing. Er memiliki titik dekat 150 cm
dan Sis memiliki titik dekat 100 cm. Hitunglah jarak paling dekat yang dapat dilihat dengan
jelas oleh:
a. eR ketika memakai kacamata Sis
b. Sis ketika memakai kacamata eR
55. Orang yang memiliki titik dekat 15 cm ingin melihat sebuah benda kecil dengan lup 25
dioptri. Lup tersebut diletakkan 2 cm didepan mata. Jika ia
u