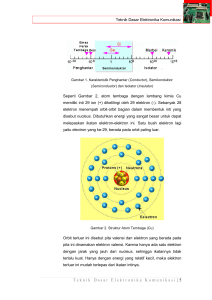
2. Gejala Transport dalam Semikonduktor

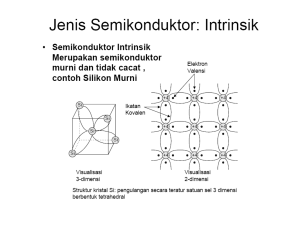
MIKROELEKTRONIKA
Gejala Transport dalam
Semikonduktor
D3 – Teknik Komputer
Universitas Gunadarma
MOBILITAS & KONDUKTIVITAS
Gambaran gas elektron dari logam
• Bagian yang gelap menyatakan
bagian yang mempunyai muatan
total positif, berasal dari inti atom
dan elektron bagian dalam yang
terikat kuat.
• Titik hitam menggambarkan
elektron luar atau elektron valensi
dari atom.
• Bayangkan suatu logam dapat
dibayangkan sebagai suatu ruang
yang mengandung kisi-kisi ion
berat, yang periodik dalam tiga
dimensi, yang saling mengikat
dengan kuat dan diantaranya diisi
oleh kawanan elektron yang
bergerak kian kemari.
• TEORI GAS ELEKTRON DARI LOGAM
– Elektron terus menerus bergerak yang arahnya
selalu berubah-ubah setelah mengalami tumbukan
dengan ion yang berat (yang hampir selalu diam).
– Jarak rata-rata antara dua tumbukan disebut jarak
bebas rata-rata.
– Gerak elektron yang acak mengakibatkan pada
suatu saat elektron yang bergerak melalui suatu
satuan luas dalam logam dalam dua arah yang
berlawanan rata-rata sama banyaknya. Oleh karena
itu arus rata-ratanya sama dengan nol.
• Kecepatan Hanyut V
– Arahnya berlawanan dengan arah medan
listrik.
– Kecepatan dalam waktu t antara dua
tumbukan adalah at, dimana a = q / m
adalah percepatan.
– Kecepatan V berbanding lurus dengan .
V = 
 (m kuadrat per detik) disebut mobilitas dari
elektron.
Rapat Arus
– Arus dalam ampere :
– Rapat arus :
I
J
A
Nq Nqv
I

T
L
Nqv
J
LA
– J dalam ampere meter kuadrat dan A adalah luas penampang
dari konduktor dalam meter kuadrat
– LA adalah volume yang mengandung N elektron, sehingga :
N
n
LA
J  nqv  v
– n adalah rapat elektron (dalam elektron per meter kubik)
–   nq adalah rapat muatan dalam coulomb meter kubik
dan v dalam meter per detik.
Konduktivitas
  nq
 adalah kondutivitas dari logam dalam (ohm meter)-1
ELEKTRON & HOLE DALAM
SEMIKONDUKTOR INTRINSIK
• Konduktivitas berbanding lurus dengan
konsentrasi n dari elektron bebas.
• Konduktor yang baik n = 10-28 elektron/meter
kubik
• Isolator n = 107
• Semikonduktor harga n diantara konduktor dan
isolator
• Ikatan Kovalen
Ikatan kovalen
Elektron valensi
 Atom Germanium mempunyai
32 elektron .
 Setiap atom menyumbangkan 4
elektron.
 Merupakan atom tentravalen.
 Mempunyai muatan listrik + 4 dalam
satuan muatan listrik elektron.
 Setiap elektron valensi dari
germanium dimiliki bersama dengan
sebuah dari empat atom germanium
yang bertetangga dekat.
Struktur kristal Ge dilukiskan secara
simbolik dalam dua dimensi
 Mempunyai konduktivitas yang
rendah
• Hole
 Pada temperatur sangat rendah
kristal berperilaku sebagai isolator.
 Pada temperatur kamar, beberapa
dari ikatan kovalen akan patah
oleh energi panas yang diberikan
kepada kristal dan konduksi
dimungkinkan.
 Energi Eg yang diperlukan untuk
mematahkan ikatan kovalen :
 Germanium : 0.72 eV
 Silikon : 1.1 eV
 Ikatan kovalen yang tidak lengkap
disebut lubang.
Kristal Germanium dengan satu
ikatan kovalen yang patah
• Dalam semikonduktor intrinsik (murni)
banyaknya lubang sama dengan banyaknya
elektron bebas.
• Konsentrasi (rapat) lubang p harus sama
dengan konsentrasi (rapat) elektron n,
sehingga :
n = p = ni
ni disebut konsentrasi atau rapat intrinsik
TAKMURNIAN
DONOR DAN AKSEPTOR
• Apabila kita tambahkan pada silikon atau germanium murni (intrinsik)
atom-atom yang bervalensi tiga atau lima maka terbentuk
semikonduktor yang takmurni, yang ekstrinsik.
• Donor-donor
– Apabila atom tak murnian mempunyai lima elektron valensi, maka atom
takmurnian akan menggeser beberapa atom germanium dari kisi-kisi
kristal.
– Empat dari lima elektron valensi akan mengisi ikatan kovalen dan yang
kelima akan terlepas dan dapat digunakan sebagai pembawa arus.
– Energi yang diperlukan untuk melepas elektron adalah :
• Ge = 0.1 eV
• Si = 0.05 eV
Contoh : antimurnian (Sb), Fosfor dan Arsenikum
– Takmurnian ini memberikan kelebihan elektron sebagai pembawa muatan
negatif, dikenal sebagai donor atau tipe-n.
• Akseptor
– Apabila suatu takmurnian trivalen ditambahkan pada semikonduktor
intrinsik hanya tiga ikatan kovalen yang diisi.
– Kekosongan yang terjada pada ikatan keempat membentuk lubang.
– Takmurnian serupa menyediakan pembawa positif oleh karen takmurnian
tersebut menciptakan lubang dan dapat menerima elektron, dikenal
sebagai akseptor atau tipe-p.
• Hukum Aksi-Massa
– Penambahan takmurnian tipe-n, mengurangi banyaknya lubang.
– Penambahan takmurnian tipe-p, menurunkan rapat elektron bebas.
 “Perkalian dari rapat muatan negatif yang bebas dan muatan yang positif,
merupakan suatu tetapan dan tidak bergantung pada banyaknya donor dan
akseptor”
np = ni2
• Dalam semikonduktor tipe-n, elektron2 disebut pembawa mayoritas
sedangkan lubang adalah pembawa minoritas.
• Dalam semikonduktro tipe-p, lubang merupakan pembawa mayoritas
dan elektron pembawa minoritas.
RAPAT MUATAN DALAM
SEMIKONDUKTOR
• Rapat muatan positif = ND + p
• Rapat muatan negatif = NA + n
• Pada semikonduktor netral, besarnya muatan positif sama dengan
besar muatan negatif :
ND + p = NA + n
• Pada semikonduktor tipe n, banyaknya elektron lebih besar dari
banyaknya lubang (n >> p) sehingga :
n n = ND
• Rapat Lubang pn dalam semikonduktor tipe-n adalah :
ni 2
pn = ---------ND
• Untuk semikonduktor tipe-p adalah :
ni 2
np = ---------NA
SIFAT ELEKTRIK
• Sifat Listrik dari Logam dan Semikonduktor :
– Logam :
• Bersifat unipolar, menghantar arus hanya dengan
muatan-muatan (elektron-elektron) yang menpunyai
satu tanda saja.
– Semikonduktor :
• Bersifat bipolar, mengandung pembawa-pembawa
arus dengan muatan yang berlawanan.
PENENTUAN KONSENTRASI PEMBAWA
• Dari teori tentang Hukum Aksi-Massa maka didapat :
“Bahwa dengan memberi takmurnian pada
semikonduktor intrinsik tidak hanya menaikkan
konduktivitas, tapi dapat juga digunakan utk
menghasilkan semikonduktor dengna pembawa listrik,
sebagian terbedar lubang atau sebagian terbesar
elektron “
• Dalam semikonduktor tipe-n, elektron-elektron disebut
pembawa mayoritas dan lubang adalah pembawa minoritas.
• Dalam semikonduktor tipe-p, lubang merupakan pembawa
mayoritas dan elektron pembawa minoritas.
PERSAMAAN ALIRAN ARUS &
PERSAMAAN POISSON
• Persamaan Aliran arus :
I
J 
A
J dalam ampere meter kuadrat,
A adalah luas penampang dari konduktor dalam meter kuadrat
• Persamaan Poisson :
d2 V

--------- = - ----dx2

 adalah permitivitas.