SOAL - JAWAB OSN Fisika 2014

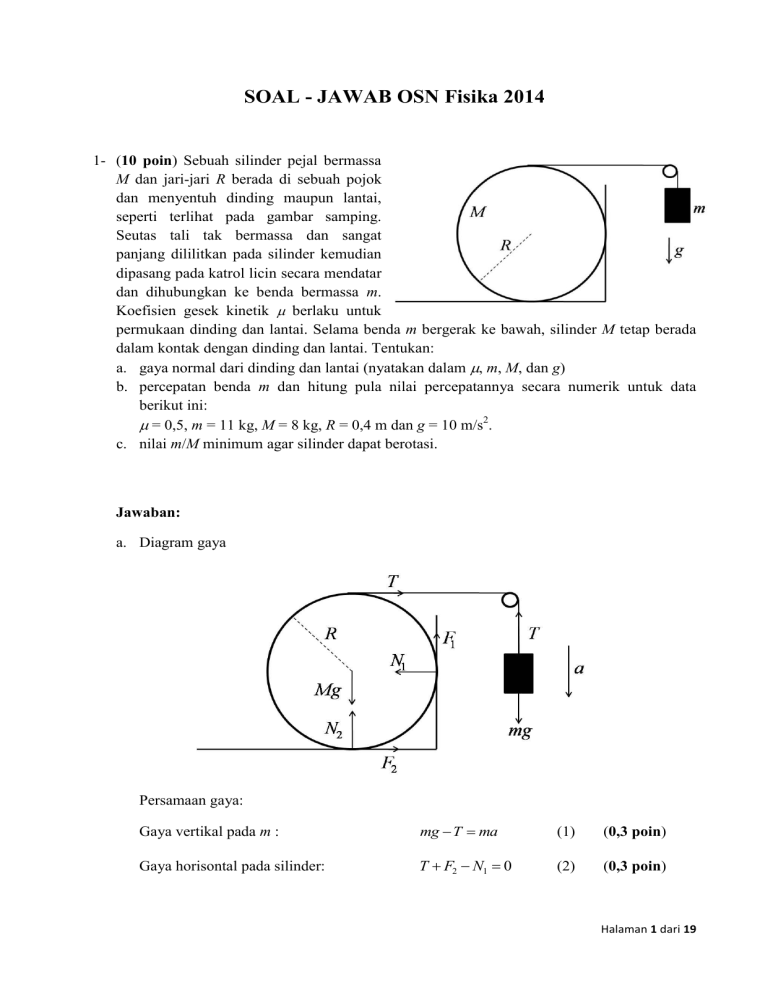
SOAL - JAWAB OSN Fisika 2014
1- (10 poin) Sebuah silinder pejal bermassa
M dan jari-jari R berada di sebuah pojok
dan menyentuh dinding maupun lantai,
seperti terlihat pada gambar samping.
Seutas tali tak bermassa dan sangat
panjang dililitkan pada silinder kemudian
dipasang pada katrol licin secara mendatar
dan dihubungkan ke benda bermassa m.
Koefisien gesek kinetik  berlaku untuk
permukaan dinding dan lantai. Selama benda m bergerak ke bawah, silinder M tetap berada
dalam kontak dengan dinding dan lantai. Tentukan:
a. gaya normal dari dinding dan lantai (nyatakan dalam , m, M, dan g)
b. percepatan benda m dan hitung pula nilai percepatannya secara numerik untuk data
berikut ini:
 = 0,5, m = 11 kg, M = 8 kg, R = 0,4 m dan g = 10 m/s2.
c. nilai m/M minimum agar silinder dapat berotasi.
Jawaban:
a. Diagram gaya
Persamaan gaya:
Gaya vertikal pada m :
mg  T  ma
(1)
(0,3 poin)
Gaya horisontal pada silinder:
T  F2  N1  0
(2)
(0,3 poin)
Halaman 1 dari 19
Gaya vertikal pada silinder:
Mg  F1  N2  0
(3)
(0,3 poin)
Gaya gesek pada dinding:
F1   N1
(4)
(0,3 poin)
Gaya gesek pada lantai
F2   N 2
(5)
(0,3 poin)
(6)
(0,3 poin)
Hubungan antara percepatan dengan percepatan sudut
a R
(7)
(0,3 poin)
Momen inersia silinder pejal terhadap sumbunya
I  12 MR 2
(8)
(0,3 poin)
Persamaan torka:
TR  F1R  F2 R  I
Delapan persamaan di atas juga mengandung delapan besaran yang belum diketahui,
yaitu T, F1, F2, N1, N2, I, a,  sehingga dengan metode substitusi, seluruh besaran
tersebut dapat diketahui.
Persamaan (1) dapat dituliskan sebagai
T  m( g  a)
(9)
Substitusi persamaan (9), (4), (5), (7) dan (8) ke persamaan (2), (3) dan (6) menghasilkan
berturut-turut
m( g  a)   N2  N1  0
(10)
Mg   N1  N2  0
(11)
(m( g  a)   N1   N2 ) R  12 MR2 (a / R)
(1 poin)
(12)
Dari persamaan (10) dan (11), nilai N1 dan N 2 dapat diperoleh sebagai
 Mg  m( g  a)
 2 1
Mg   m( g  a)
N2 
 2 1
N1 
(13)
(14)
Masukan harga a dari pers (15) didapatkan:

4m  M  m
N1  
2
2
 2m 2     1  M   1


Mg

(1,3 poin)

M  2m  3m
N 2  
2
2
 2m 2     1  M   1

 Mg

(1,3 poin)







Halaman 2 dari 19
b. Dengan memasukkan persamaan (13) dan (14) ke dalam persamaan (12), akhirnya
percepatan m dapat ditentukan sebagai
a
m(2 2    1)  M (  2   )
g
m(2 2    1)  12 M (  2  1)
(15)
Dengan memasukkan nilai-nilai besaran di atas,
a = 3,125 m/s2
(1 poin)
(1 poin)
Nilai a di atas tidak bergantung pada R.
c. Agar silinder di atas berotasi, maka benda m harus bergerak ke bawah,  a  0.
Sehingga a minimum 
a=0
(0,5 poin)




m 2 2    1  M  2    0
2  
m

 
2
 M  min 2    1
atau
(1,5 poin)
Halaman 3 dari 19
2- (13 poin) Perhatikan gambar di bawah ini. Sebuah bola billiard berjari-jari R diletakkan
pada posisi (a, b) dari ujung kiri atas meja (lubang A). Panjang dan lebar bagian dalam meja
berturut-turut adalah P dan L. Seorang siswa ingin memasukkan bola tersebut ke dalam
lubang C dengan memukulnya oleh gaya sesaat F pada sudut  terhadap sisi AB. Waktu
kontak pemukul dengan bola adalah t0 dan asumsikan seluruh impuls yang diberikan
pemukul dikonversi menjadi momentum bola. Siswa tersebut berencana untuk memantulkan
bola tersebut dua kali yaitu dipantulkan oleh sisi AB dan sisi BD, sampai akhirnya masuk ke
lubang. Lubang pada meja dibuat sedemikian sehingga titik tengah lubang tersebut berada
tepat pada ujung-ujung bagian dalam meja. Dan ketika bola masuk lubang, pusat massa bola
dianggap berada pada pusat lubang.
A
B
C
D
Tentukanlah:
a. tan  agar bola tepat masuk di lubang C (nyatakan dalam b, P, R, dan a).
b. S1 yaitu jarak yang ditempuh bola sebelum menumbuk dinding AB.
c. S 2 yaitu jarak yang ditempuh bola setelah menumbuk dinding AB dan sebelum
menumbuk dinding BD.
d. S3 yaitu jarak yang ditempuh bola setelah menumbuk dinding BD dan sebelum
memasuki lubang.
e. Jika tumbukan antara bola dan dinding adalah lenting sebagian dengan koefisien restitusi
e, tentukan kecepatan bola sesaat sebelum masuk ke dalam lubang (nyatakan dalam
F , t0 , e, m, k , R, S1 , S2 , dan S3.
(Asumsikan energi yang hilang akibat rotasi adalah kmRd dimana k adalah konstanta
penghambat rotasi, m adalah massa bola, R adalah jari-jari bola, dan d adalah jarak
yang ditempuh bola.)
Halaman 4 dari 19
Jawab:
A
B
C
D
(0,5 poin)
a. Misalkan tumbukan antara bola dengan dinding terjadi dengan koefisien restitusi e ,
maka kita dapatkan
1
tan   tan 
(0,5 poin)
e
1
tan   tan 
(0,5 poin)
e
sehingga kita punya
(0,5 poin)
tan  tan 
Menggunakan trigonometri dan geometri, kita dapatkan:
y
b
y
tan   
 1
(0,5 poin)
R L  R ex1
a  x  x1  L  R
y1  y  P  R
dimana variabel yang tidak diketahui adalah x, y, x1 , y1 dan  . Dengan eliminasi dan
substitusi, kita dapatkan:
tan  
eb  P  R
L  R 1  e  ea
(0,5 poin)
Halaman 5 dari 19
dan
x
L  R 1  e  ea
e
x1 
PR
b
L  R P  R  b  a( P  R)
( P  R)  eb
P  R  eb
a
(1  e) 
LR
dan
y
dan
y1  e
( L  R)( P  R  b)  a( P  R)
(1  e)( L  R)  ea
(0,5 poin)
b. Sehingga:
S1  b csc
 L  R 1  e   ea 
 b 1 

eb  P  R


c. S 2
2
L  R P  R  b  a( P  R)

( P  R)  eb
(1,5 poin)


eb  P  R

1   e
 L  R 1  e   ea 
2
(1,5 poin)
S 3  L  R sec 
d.


eb  P  R

 ( L  R) 1  
 L  R 1  e   ea 
2
(1,5 poin)
e. Kemudian, dengan menggunakan kekekalan energi
1 2 1 2
mv0  mv1  Eloss
2
2
1
 mv12  kmrd
2
(1 poin)
v02  v12  2krS1
(1 poin)
v1  v02  2kRS1
(1 poin)
mv0  Ft 0

v0 
Ft 0
m
(0,5 poin)
kita dapatkan
Halaman 6 dari 19
v1 
F 2 t 02
 2kRS1
m2
(0,5 poin)
Kecepatan setelah tumbukan untuk dinding atas adalah ev1 . Dengan menggunakan
kekekalan energi untuk jalur S 2 dan S3 , kita dapatkan:
vakhir  e 4
F 2 t 02
 2kR e 4 S1  e 2 S 2  S 3
2
m


(1 poin)
3- (15 poin) Dua buah partikel A dan B dapat bergerak tanpa gesekan di sepanjang sumbu y dan
partikel C dapat bergerak tanpa gesekan di sepanjang sumbu x. Partikel B dan C terhubung
melalui suatu batang tegar yang tak bermassa dengan panjang L , sedangkan partikel A dan
C terhubung melalui suatu batang tegar tak bermassa dengan panjang L 3 . Terdapat suatu
engsel licin yang menghubungkan kedua ujung batang tersebut di C (lihat gambar).
Diketahui massa ketiga partikel, mA  mB  mC  m dan pada saat awal, 1 (0)   6 rad ,
1 (0)  2 (0)  0 rad s , dimana 1  d1 dt dan 2  d2 dt
y
g
A
1
L 3
B
2
L
C
O
x
Tentukan:
a. posisi masing-masing partikel (nyatakan dalam sudut 1 dan  2 ) dan tentukan hubungan
antara sudut 1 dan  2
b. energi total dari sistem dinyatakan dalam sudut  2 dan 2
Halaman 7 dari 19
c. kecepatan dan percepatan dari masing-masing partikel ketika partikel B sampai di titik O
untuk yang pertama kali
Jawab:
y
A
1
L 3
yA
B
L
2
yB
C
O
x
xC
a. Dari gambar terlihat bahwa
y A  L 3 cos1
yB  L cos 2
(1)
(3 poin)
(2)
(1 poin)
(3)
(1,5 poin)
(4)
(0,5 poin)
(5)
(1,5 poin)
xC  L 3 sin 1  L sin  2
sehingga kita dapatkan hubungan antara sudut 1 dan  2 adalah
3 sin 1  sin 2
b. Energi potensial sistem adalah
EP  mgy A  mgyB
 mgL
 mgL


3 cos1  cos  2

3  sin 2  2  cos 2

Energi kinetik sistem adalah,
1
EK  m  v yA2  v yB 2  vxC 2 
2
Dengan menggunakan persamaan (1), kita dapatkan
v yA  1 L 3 sin 1
v yB  2 L sin  2
vxC  2 L cos 2
Halaman 8 dari 19
Dan dari persamaan (2) , kita dapatkan
1 
cos 2
3  sin 2  2
2
(6)
(0,5 poin)
(7)
(1 poin)
(8)
(1 poin)
Substitusi persamaan (5) dan (6) ke persamaan (4), kita dapatkan
1
EK  mL2  312 sin 2 1  2 2 sin 2  2  2 2 cos 2  2 
2
 sin 2  2 cos 2  2

1
 mL22 2 
 1
2
2
 3  sin  2

 3  sin 4  2 
1
 mL22 2 

2
2
 3  sin  2 
Jadi energi total untuk sistem adalah
E  EK  EP
 3  sin 4  2 
1
 mL22 2 
  mgL
2
2
 3  sin  2 

3  sin 2  2  cos  2

c. Karena sistem konservatif, maka energi total sistem kekal. Pada saat awal, energi kinetik
sistem nol, sehingga energi pada saat keadaan awal adalah
(0,5 poin)
Eawal  2mgL
dan saat partikel B sampai di titik O, 2   2 rad ,
1
Eakhir  mL22 2  2mgL
2
(0,5 poin)
Dengan menggunakan kekekalan energi, didapatkan
2 

2g
2 2
L

(9)
(0,5 poin)
(10)
(1,5 poin)
Substitusi ke persamaan (5) dan (6), kita dapatkan
v yA  0

v yB   2 gL 2  2

vxC  0
Halaman 9 dari 19
y
TAC
A
1
L 3
mg
TBC
C
L
B
TCB
O
x
TCA
mg
Hukum II Newton untuk partikel saat B di titik O adalah
TAC cos1  mg  ma yA
mg  ma yB
(11)
(0,5 poin)
TCB  TCA sin 1  maxC
sehingga kita dapatkan
a yB   g
Dari persamaan (5) dan (6), kita punya
a yA  2   


2
 2 sin 2 2  22 2 cos 2 2  2 sin 2 2 2 

2
2
2 3  sin  2 

L
a yB  2    L 2 2 cos 2   2 sin  2 
(12) (0,9 poin)
axC  2   L  2 2 sin  2   2 cos 2 
dengan  2  d2 dt . Karena ketika partikel B berada di titik O, 2   2 rad , maka
2  
dan

g
L

a yA  2 g 2  1

a xC  2 g 2  2

(13)
(0,2 poin)
(14)
(0,4 poin)
Halaman 10 dari 19
4- (20 poin) Sebuah kapasitor keping sejajar mempunyai luas penampang A dan terpisah sejauh
d, serta tinggi a. Ruang diantara kapasitor berisi udara dengan permitivitas anggap sama
dengan ruang hampa yaitu 0. Kapasitor kemudian dihubungkan dengan sebuah baterai yang
memiliki tegangan V0. Kemudian baterai diputus, muatan pada kapasitor dipertahankan tetap
sebesar Q0, kemudian sebuah lembaran dielektrik padat dengan luas yang sama, A, dan tebal
l (dimana l < d) serta konstanta dielektrik K1 disisipkan tepat di tengah kapasitor. Hitung:
(a) muatan induksi pada dielektrik!
(b) medan listrik pada ruang diantara dielektrik dan plat!
(c) medan listrik pada dielektrik!
(d) beda potensial kapasitor setelah dielektrik dimasukkan!
(e) Tentukan kapasitas kapasitor setelah dielektrik dimasukkan!
Dielektrik padat kemudian ditarik dan kapasitor selanjutnya dihubungkan kembali dengan
baterai semula dengan tegangan V0. Kapasitor ini kemudian dicelupkan kedalam cairan
dielektrik dengan konstanta dielektrik K2 dan massa jenis .
(f) Tentukan ketinggian cairan yang naik diantara kedua plat sejajar!
Kapasitor diangkat dari cairan, baterai kemudian dilepas dan kemudian pada plat sejajar
diberi muatan sebesar Q0.
(g) Hitung kembali ketinggian cairan yang naik diantara kedua plat sejajar pada kondisi
terakhir!
Ketentuan:
Semua jawaban akhir harus dalam V0 atau Q0 dan ukuran geometri serta konstanta dielektrik
yang sesuai.
Jawab:
(a). Kapasitas kapasitor pada kondisi vacuum:
Besar muatan pada kapasitor:
C
0 A
(1 poin)
d
Q0 = CV =
0 A
d
V0
(1 poin)
Muatan induksi pada dielektrik:
Qind = Qo ( 1 -
1
)
K
(2 poin)
Halaman 11 dari 19
(b). Medan listrik pada ruang diantara dielektrik dan plat:
Medan listrik tidak berubah yaitu:
E0 
Q0 V0

0 A d
(2 poin)
(c). Carilah medan listrik pada dielektrik!
Ed  E0 / K1 
Q0
K1 0 A
(2 poin)
(d). Tentukan beda potensial setelah dielektrik dimasukkan!
V   E  dl  E0 (d  l )  Ed l  E0 (d  l )  E0l / K1
V  E0 (d  l  l / K1 ) 
Q0
(d  l  l / K1 )
0 A
(2 poin)
(e). Kapasitas setelah dielektrik dimasukkan!
C
Q0
0 A
Q


Q0
V
(d  l  l / K1 ) (d  l  l / K1 )
0 A
(2 poin)
(h)
a
x
Adanya muatan pada kapasitor akan menarik cairan ke atas sampai terjadi keseimbangan
antara gaya listrik dan gaya gravitasi. Misal hal ini terjadi pada ketinggian x.
Ambil lebar kapasitor adalah b = A/a.
Kapasitas kapasitor menjadi:
C
 0b
d
[ K 2 x  (a  x)] 
 0b
d
[( K 2  1) x  a]
Halaman 12 dari 19
Gaya listrik:
Fe  
d ( 1 CV 2 )
b
dW
 2
 0 ( K 2  1)V 2
dx
dx
2d
Pada kondisi setimbang, gaya listrik ini sama dengan gaya berat dielektrik, maka:
 0b
2d
 0b
2d
 0b
2d
( K 2  1)V 2  mg
( K 2  1)V 2   (Vol cair) g
( K 2  1)V 2  bdhg
h
Sehingga ketinggian cairan menjadi:
0
2 gd
2
( K 2  1)V 2
(4 poin)
(i). Apabila muatan dipertahankan sebesar Q0,
Gaya listrik:
Fe  
d ( 1 CV 2 ) Q02  dC 
dW
 2



dx
dx
2C 2  dx 
Q02 ( K 2  1)d
Fe 
2b[( K 2  1) x  a]2  0
Pada keadaan keseimbangan:
h
Q02 ( K 2  1)
2  gb2 [( K 2  1) x  a]2  0
Persamaan pangkat tiga ini dapat diselesaikan dengan menggunakan pendekatan h = x
bernilai rendah:
h
h

K 2  1h  a2
K 2  1
2

dengan

h  2aK 2  1h  a
2
2

Q02 K 2  1
2 gb 2 0

2aK 2  1h  a 2
2aK 2  1h 2  a 2 h    0
Ambil hasil akar h yang positif:
Halaman 13 dari 19
Q02 K 2  1
 a  a  8a
2 gb 2 0
2
h
2
 a 2  a 4  8a K 2  1
4aK 2  1
h
atau
4
4aK 2  1
(4 poin)
5- (22 poin) Sebuah lintasan memiliki 2 buah loop lingkaran beradius R yg terpaut jarak
tertentu (seperti pada gambar dibawah). Loop setengah lingkaran yg kiri permukaannya licin,
sedangkan sisa lintasan yaitu lintasan lurus dan loop seperdelapan lingkaran yang kanan
permukaannya kasar dengan besar koefisien gesek statis dan kinetis yg sama, . Pada
lintasan ini, akan dilakukan 2 kali percobaan.
Percobaan pertama, sebuah benda X bermassa m, berjari-jari r, memiliki momen inersia βmr²
dilepaskan dari keadaan diam pada puncak lintasan di sebelah kanan.
(a) Tentukan syarat μ (koefisien gesek) lintasan tersebut agar benda memiliki energi kinetik
maksimum pada saat melewati titik A!
Mulai saat ini dan seterusnya (hingga percobaan kedua), gunakan koefisien gesek minimum
yang didapat di (a) untuk lintasan kasar.
(b) Benda X akan menggelinding hingga melewati titik B. Hitung kecepatan benda X di titik
B!
(c) Benda X akan menaiki loop kiri hingga titik tertinggi. Berapakah s, panjang lintasan
(diukur dari B ke arah kiri mengikuti bentuk lintasan) yg ditempuh benda?
(d) Benda tersebut akan bergerak kembali ke titik B, dan kemudian bergulir sepanjang
lintasan BA. Tentukan nilai L, (di sepanjang lintasan BA) sehingga benda X dapat
mencapai titik A dalam kondisi yg sudah tidak slip!
Mulai saat ini dan seterusnya (hingga percobaan kedua), asumsikan benda X adalah silinder
berongga, sehingga β adalah suatu nilai numeris, dan gunakan nilai numeris tersebut untuk
soal-soal di bawah ini.
Halaman 14 dari 19
(e) Jelaskan keadaan gerak benda X secara kualitatif jika :
1) Panjang BA < L
2) Panjang BA > L
Percobaan kedua dilakukan. Di sini, diperkenalkan sebuah benda titik Y bermassa m juga,
namun tidak memiliki momen inersia.
Lintasan masih memiliki kekasaran sesuai dgn hasil (a).
INGAT, masukkan nilai numeris β!
Pada percobaan kedua, hal yang sama dilakukan seperti percobaan pertama. Namun, disaat
benda X berada pada titik B (berarah gerak ke kanan), benda Y di lontarkan dari titik A
(berarah gerak ke kiri) dengan kecepatan v (besarnya mengikuti hasil (b)).
(f) Tentukan d, letak tumbukan benda X dan Y(diukur dari titik A ke arah ke kanan)!
(g) Tentukan pula τ, waktu bertumbukan mereka (diukur dari saat benda X di B dan benda Y
di A)!
(h) Tumbukan terjadi secara sentral dan elastik. Tentukan kecepatan benda-benda tersebut
sesaat setelah tumbukan!
(i) Analisis gerakan kedua benda setelah tumbukan dan jawablah setiap pertanyaan berikut
ini dengan bukti-bukti kuantitatif :
1) Apakah benda X dapat mencapai kondisi tidak slip sebelum sampai di titik B?
2) Apakah benda Y berhenti bergerak sebelum menaiki loop kanan?
3) Akankah kedua benda tersebut bertumbukan untuk kedua kali-nya? Jika ya, tentukan
kecepatan masing2 benda sesaat setelah tumbukan kedua!
(j) Jelaskan konfigurasi (kecepatan dan posisi) paling akhir benda X dan Y!
Catatan: Jawaban dari soal2 diatas hanya boleh dinyatakan dalam R, m, r, dan g.
Khusus (a)-(d), jawaban boleh juga dinyatakan dalam β.
Jawaban:
(a) Agar benda memiliki energi kinetik maksimum, gaya gesek tidak boleh melakukan kerja.
Kemungkinan 1: Licin
μ = 0 (Tidak memenuhi, karena lintasan seharusnya kasar)
(0,2 poin)
Kemungkinan 2: Tidak slip
Hukum Newton II :
Translasi :
mg sin θ – f = m.a ........(1)
N = mg cos θ
.........(2)
(0,2 poin)
(0,2 poin)
Halaman 15 dari 19
f.r = I.α = βmr².α ........(3)
Rotasi :
a = αr.......(4)
dari konsep tidak slip :
Dari Persamaan (1), (3), dan (4) :
Kita tahu
(0,2 poin)
f=
(0,2 poin)
mg sin θ
f ≤ μ.N
mg sin θ ≤ μ.mg cos θ
Maka, menggunakan pers (2) :
μ≥
tan θ
(0,2 poin)
(0,2 poin)
θ terbesar pada saat kondisi awal : θ = 45o
μ≥
Maka....
.........(*)
(ANSWER)
(0,4 poin)
(b) Karena energi kekal, maka :
mgh = ½ mv2 + ½ Iω2
..........(5)
(0,5 poin)
Dari geometri, didapat h = (R - r) (1- cos(45o) )
= ½ (R – r) (2 -
) .........(6)
(0,5 poin)
.......(7)
(0,5 poin)
v = ωr
Konsep tidak slip :
Dari (5), (6), dan (7), serta memasukkan nilai I, didapat:
v=
..... (**)
(ANSWER)
(0,5 poin)
(c) Karena lintasan di sebelah kiri titik B licin, maka kecepatan sudut benda X tetap konstan
selama menaiki lintasan.
(0,3 poin)
Hukum Kekekalan Energi:
½ mv2 + ½ I2 = mgh’ + ½ I2 ....(8)
Dari geometri didapat :
s = θ’.R
.........(9)
(0,4 poin)
dan
(0,3 poin)
h’ = (R-r)(1- cos θ’)
θ’ = arc cos (1- h’/(R-r)) ........(10)
(0,5 poin)
Dari persamaan (8), (9), (10), dan (**), didapat :
s = R arc cos (
)
(ANSWER)
(0,5 poin)
Halaman 16 dari 19
(d) Hukum kekekalan momentum sudut pd titik kontak bola dengan lantai :
mvr - βmr²ω = (1+β) mv’.r
........(11)
(0,4 poin)
Persamaan (11) juga bisa didapat dengan menggunakan impuls linear dan impuls sudut
pada bola.
v’ =
v=
......(12)
v’2 = v2 + 2(a)L ......(13)
Kinematik:
(0,4 poin)
(0,4 poin)
Dari hukum Newton, dengan mudah didapat :
a = - μg
.......(14)
(0,2 poin)
Dari (12), (13), dan (14), serta memasukan (*), didapat :
L=
........ (***)
β=1
(e) Silinder berongga :
(ANSWER)
.....(15)
(0,6 poin)
(0,5 poin)
Substitusi (15) ke (12) dan (****)
v’ = 0 dan L = v2/g
Didapat :
(0,5 poin)
1) Jika lintasan terlalu pendek : Benda X masih slip saat menaiki loop kanan
(ANSWER)
(0,5 poin)
2) Jika lintasan terlalu panjang : Benda X akan berhenti pd jarak L sehingga tidak
dapat mencapai titik A
(ANSWER)
(0,5 poin)
(f) Benda X dan Benda Y mendapat gaya linear yg sama, sehingga mereka memiliki gerak
translasi yg persis sama
Lx = Ly = v.t - ½. μg.t2
(0,5 poin)
Sehingga
d = L/2 = v2/2g
(0,5 poin)
Subs (**)
d=
(ANSWER)
(1 poin)
Halaman 17 dari 19
(g) karena pers (15),
μ=½
(0,2 poin)
Lx + Ly = L
(0,2 poin)
2vτ - ½ gτ2 = L = v2/g
Sehingga:
½ gτ2 - 2vτ + v2/g = 0
(0,2 poin)
τ = (v/g)(2 ±
(0,2 poin)
)
Perhatikan bahwa waktu yg dibutuhkan benda utk berhenti total (tanpa adanya benda Y):
tstop = 2L/v = 2v/g
(0,2 poin)
Karena nilai τ < tstop, maka haruslah diambil solusi negatif :
τ = (v/g)(2 -
)=
(ANSWER)
(0,2 poin)
(0,3 poin)
(h) Sekarang, kita gunakan perjanjian tanda (+) untuk v ke kanan dan (-) untuk v ke kiri
(+) untuk  ke clockwise dan (-) untuk  counter-clockwise.
Misal :
Notasi i menunjukkan sesaat sebelum tumbukan dan x, y adalah benda X dan benda Y
Maka
vix = v – a. τ =
v=+
........(16)
Karena motion translasi x dan y sama, maka viy = -vix = -
(0,3 poin)
(0,3 poin)
Dan karena β = 1, kecepatan sudut juga memiliki perumusan yg persis sama, hanya
berbeda faktor r.
(0,2 poin)
Maka
ωix = -
(0,3 poin)
Karena massa nya sama, maka, tumbukan sentral dan elastik menyebabkan kedua benda
bertukar kecepatan translasi
(0,3 poin)
Maka
ωx = ωix = -
(ANSWER)
vx = viy = -
(ANSWER)
(0,7 poin)
vy = vix = +
(ANSWER)
(0,7 poin)
(0,7 poin)
Halaman 18 dari 19
(i) 1) Tidak slip :
vx’ = ωx’.r (Perhatikan bahwa + dan – penting di sini!)
Karena tepat saat setelah tumbukan, nilai vx = ωx.r, maka benda X langsung bergulir
tanpa slip tanpa proses gesekan.
Jawaban : Ya
(ANSWER)
(1 poin)
2) Karena benda Y melanjutkan gerak lurusnya (hanya arah yg berbalik), maka benda Y
akan berhenti bergerak tepat di titik A.
(vy)2 = 2(μg)l
Bukti :
l=
=d
Jawaban : Ya
(ANSWER)
(1 poin)
3) Benda X akan mengalami gerakan yg sama dengan gerakan awalnya. Namun, saat ini
energi benda X lebih kecil. Sehingga, benda X akan berhenti pada jarak yg lebih kecil
dari L.
Karena
(16)...... vx =
v
dan
(***)....... Lstop ~ v2
(0,5 poin)
Maka L’ = L/2 (di tengah, tempat tumbukan)
dan saat benda X sampai di titik ini pd kondisi diamnya, benda Y telah meninggalkan
titik ini dan akan berhenti di titik A dan tumbukan kedua tidak akan pernah terjadi.
Jawaban : Tidak
(j) Benda X diam tepat di tengah2 lintasan
Benda Y diam tepat di titik A
(ANSWER)
(1 poin)
(ANSWER)
(0,8 poin)
(ANSWER)
(0,7 poin)
Halaman 19 dari 19