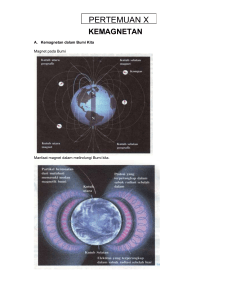
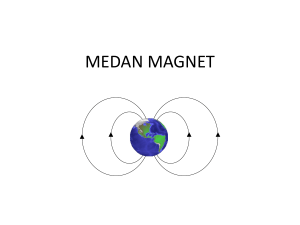
Medan Magnet

MAGNETOSTATIK
Umiatin, M.Si
Jurusan Fisika UNJ
Medan Magnet




Magnet pertamakali ditemukan dalam bentuk
batuan (magnetite / Fe3O4)
Hadir selalu dlm dua kutub, Utara dan Selatan
Hubungan antara magnet dgn listrik mulai
ditemukan melalui percobaan Oersted (jarum
kompas menyimpang disekitar kawat berarus)
Sementara hubungan antara listrik dgn magnet
ditemukan oleh Faraday dan Joseph Henry
Medan Magnet dan Gaya Magnet


Medan magnet bisa dihasilkan
bahan magnet permanen dan
oleh elektron yg bergerak.
Medan magnet B ditunjukkan
arahnya oleh arah jarum kompas
dan arahnya digambarkan dgn
garis-garis medan magnet (keluar
dari kutub utara masuk di kutub
selatan)

Medan magnet bisa dinyatakan dalam gaya
magnet. Muatan yg bergerak di dalam medan
magnet akan mengalami gaya magnet :




Gaya magnet FB sebanding dgn muatan dan kecepatan
partikel
arah gaya FB bergantung arah kecepatan partikel dan
arah medan magnet B
Arah gaya tegak lurus terhadap kecepatan dan arah
medan magnet
Besar gaya sebanding dengan harga sin , dimana 
adalah sudut antara arah kecepatan dan medan magnet
FB = q V x B
Satuan Medan Magnet : Tesla (T)

1 T = 1 N/ (c m/s) = 1 N/ (A.m)

1 T = 104 Gauss
Arah Gaya Magnet
Contoh 1

Sebuah elektron dalam tabung televisi
bergerak pada sumbu x dgn kecepatan 8 x
106 m/s. Pada tabung tersebut bekerja
medan magnet dgn arah 60o terhadap sb x
dan terletak pada bidang xy sebesar 0.25 T.
Berapa besar dan kemana arah gaya magnet
yg dialami elektron tsb?
Gaya Magnet pada kawat berarus
Medan magnet keluar bidang => titik
 Medan magnet masuk bidang => kros tanda
silang)
 Segmen kawat L, gaya pada satu muatan :
F B = q Vd x B
total didalam kawat n A L :
F B = q Vd x B n A L
Karena I = n q Vd A
FB = I L x B
L = vektor

misal, segmen ds sembarang arah :
dFB = I ds x B
Total gaya sepanjang kawat :
FB = I ab ds x B
Momen pada loop berarus didalam
medan magnet
Misal loop persegi :
 pada kawat 1 dan 3 F= 0
 Pada 2 dan 4 :
 F = I aB dgn arah keluar
dan masuk
 Kedua gaya membentuk
momen :
 max= F2 b/2 + F4 b/2

=IaBb

= I ab B

=IAB
 Dimana A = luas Loop







Bila arah B membentuk sudut terhadap
A:
 = F2 b/2 sin  + F4 b/2 sin 
= I a B b/2 sin  + I a B b/2 sin 
= I ab B sin 
= I A B sin 
=IAxB
Selanjutnya besaran IA didefinisikan
sebagai momen magnetik 
=IA
Contoh



Sebuah koil berukuran 5 x 10 cm terdiri dari
25 lilitan. Koil tsb dialiri arus 0.5 A dan
Berada pd medan magnet uniform sebesar
0.3 T. Tentukan :
Besar momen magnetiknya
Besar torka yg dihasilkan
Gerak partikel bermuatan didalam
medan magnet







Sebuah partikel positif bermuatan q
bergerak dalam medan magnet
homogen B :
Partikel bergerak melingkar :
Gaya magnetik = gaya centripetal
FB = mv2/r
q v B = m v2/r
r = mv /(q B)
= v/r = qB/m
m/q = B r/v
 = frekuenci anguler
T = 2r/v = 2m/(qB)
contoh

Sebuah elektron ditembakan pada medan
magnet homogen. Dari keadaan diam
elektron dipercepat dgn bedapotensial 350
kV. Bila elektron membentuk lingkaran dgn
jari-jari 10 cm,Tentukan besar medan
magnet! Tentukan juga frekuensi angularnya!
Partikel bergerak di dlm medan
magnet dan listrik




Partikel akan mengalami gaya magnet keatas : q V
xB
Partikel akan mengalami gaya listrik kebawah : q
E,
Jika setimbang :
q v x B = q E => v = E/B
Efek Hall

Pada konduktor yg
dialiri arus listrik yg
berada pada medan
magnet akan terjadi
defleksi (polarisasi)
pembawa muatan
sehingga muncul
medan Hall
Gaya magnet akan seimbang dgn gaya listrik yg
dihasilkan :
 q v d B = q EH
 Jika jarak separasi d :
 VH= EH d
 q vd B = q VH/d
VH = vd B d

Karena I = n q vd A
=> vd= I/nqA
VH = I B d/ (nqA)
karena A = t d
= I B / (nq t)
= RH IB/t
RH konstanta Hall RH = 1/ nq
Medan Magnet
(lanjutan)
Hukum Biot -Savart

Biot dan savart menyelidiki besar medan db disekitar
kawat berarus ds :





Vektor db tegak lurus terhadap ds dan r
Besar db berbanding terbalik dengan r2
Besar db sebanding dgn arus dn panjang ds
Besar db sebanding dengan sin ,sudut antara ds dan r
Secara matematis hukum Biot-Savart:
Db = o I ds x r
4 r2
o = permeabilitas ruang hampa
= 4 x 10-7 T m/A

Untuk keseluruhan panjang kawat :

Ada kemiripan dgn medan listrik tetapi ada perbedaannya:


Arah medan
Penyebabnya (muatan terisolasi)
Contoh :

Tentukan besar medan magnet dititik P oleh
kawat lurus berarus I yang berjarak a dari
kawat sepanjang L!


Menentukan arah
medan magnet
disekitar kawat ;
Aturan tangan kanan :
Contoh 2

Sebuah loop berjari-jari R dialiri arus konstan
sebesar I, tentukan medan magnet dititik P
yang berjarak x dari sumbu pusat loop
Gaya magnetik antar dua kawat
konduktor
Kawat 1 mengalami gaya oleh
karena medan magnet kawat 2 :
F1 = I1 L B2

Pada kawat dua menghasilkan
medan B2 :
 B2 = o I2
2a
Sehingga :
F1 = I1 L o I2
2a
 Pada kawat 2 akan muncul gaya
yg sama besar tetapi berlawanan
arah
 Arus searah tarik menarik,
berlawanan tolak menolak

F= o I1 I2
L 2a
Hukum Ampere
Oersted menunjukkan
arah medan magnet
disekitar kawat berarus
 Arah medan magnet
memutari kawat
 Bila ds adalah lintasan
dalam lingkaran dan
dihitung B. ds maka :
 B . ds = B  ds = B 2a
= oI 2a
2a
 B . ds = oI

<=
Hukum Ampere

Integral garis dari B.ds pada suatu lintasan
tertutup adalah sama dengan oI, dimana I
adalah total arus yang dilingkupi oleh lintasan
tersebut
Medan magnetik pada toroid dan
solenoid

Toroida

B di Solenoid :




Lemah diluar
Kuat didalam
Solenoid ideal
ditengahnya uniform
Menyerupai magnet
batang

Loop ampere
memberikan :





Lintasan 2,3,4 nol
Lintasan1 ada nilainya
B.ds = oI N
B L = oI N
B = oI N/L
Flux magnetik
Mirip dgn flux listrik :
B= B. dA
Untuk B uniform dan A datar :
B= B A cos 

Satuan flux magnetik T.m2 atau weber (wb)
Contoh

Hitung fluks magnetik pada
sebuah loop persegi
berukuran ax b yang
ditempatkan sejauh c dari
kawat panjang berarus I
Hukum Gauss

Total fluks magentik dari
suatu permukaan tertutup
adalah nol

KOnsekuensi dari tidak
adanya monopole

Tentukan medan
Magnet di titik P