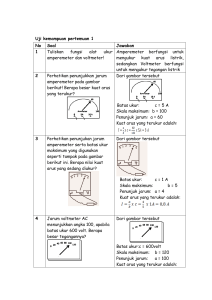
Fungsi Pemaksa Tangga Satuan Pada

Oleh : Danny Kurnianto; Risa Farrid Christianti
Sekolah Tinggi Teknologi Telematika Telkom
Purwokerto
Pendahuluan
 Setelah kita mempelajari tanggapan alamiah dari
suatu rangkaian RL atau RC, yaitu tanggapan saat
sumber (tegangan atau arus) ditiadakan secara tibatiba, maka pada pertemuan kali ini kita akan belajar
mengenai tanggapan pemaksa dari rangkaian RL atau
RC.
 Tanggapan pemaksa terjadi ketika sumber (tegangan
atau arus) diterapkan secara tiba-tiba pada rangkaian
RL atau RC.
1. Fungsi Pemaksa Tangga Satuan
 Definisi : fungsi pemaksa tangga satuan adalah sebuah
fungsi yang sama dengan nol bila semua harga
argumennya lebih kecil dari nol dan sama dengan satu
bila harga argumennya lebih besar dari nol (positif).
 Jika (t-t0) adalah argumen, dan u adalah fungsi tangga
satuan , maka u(t-t0) = 0 untuk semua t yang lebih
kecil dari t0 dan sama u(t-t0) = 1 untuk semua t yang
lebih besar dari to.
 Definisi matematis untuk menggambarkan fungsi
tangga satuan di atas adalah :
 0 t t 0
 (t  t0 )  
 1 t t0 ………………………..(1)
Grafik fungsi tangga satuan u(t-t0) seperti yang
ditunjukkan pada Gambar 1.
u(t-t0)
1
0
to
t
 Jika waktu diskontinuitas (perpindahan keadaan)
terjadi saat to = 0 , maka fungsi tangga satuan menjadi
u(t-0) atau yg lebih sederhana lagi menjadi u(t).
 Hal ini ditunjukkan oleh definisi matematisnya :

u (t )  
 1 t 0
0 t 0
…………….(2)
Grafik fungsi tangga satuan u(t) ditunjukan pada
Gambar 2.
u(t)
1
t
0
Gambar 2. Fungsi tangga satuan u(t)
 Fungsi tangga satuan itu sendiri tidak berdimensi, jika
ingin dinyatakan sebagai sebuah tegangan, maka perlu
mengalikan u(t-t0) dengan suatu tegangan konstan
(V). Jadi v(t) = Vu(t-t0).
Gambar 3. Rangkaian ekivalen dari Vu(t-t0)
 Jika ada suatu fungsi tangga satuan sebagai berikut :
u(t-t0)-u(t-t1), maka dapat didefinisikan secara
matematis sebagai berikut :
0

u (t )  1
0

t  t0
t0  t  t1
t  t1
……………..(3)
u(t)
1
t
t0
t1
 Contoh 1
Berapa nilai dari fungsi tangga satuan berikut ini
pada t = 1,5 s.
a.) 2u(t-2) + u(t+1) + u(t-1)
b.) [u(t-1) – u(1-t)] u(t+1)
2. Untuk rangkaian pada gambar dibawah ini, carilah
nilai v1 pada t :
a.) -5 s
b.) -1 s
c.) 1 s
1.
 Jawab:
Dengan t = 1,5 s, maka fungsi tangga satuan
a.) 2u(1,5-2) + u(1,5+1) + u(1,5-1)
2.0 + 1 + 1 = 2
b.) [u(1,5-1) – u(1-1,5)] .u(1,5+1)
[1 – 0]. 1 = 1
2. Nilai v1, pada
a.) t = -5 s, hasilnya adl nilai v1 = 50 V
b.) t = -1 s, hasilnya adl nilai v1 = 90 V
c.) t = 1 s , hasilnya adl nilai v1 = 34 V
1.
2. Tanggapan Lengkap Rangkaian
RL dan RC
 Tanggapan lengkap suatu rangkaian RL dan RC adalah
penjumlahan tanggapan alamiah dan tangapan
paksaan rangkaian.
 Perhatikan rangakain RL sederhana dibawah ini:
Gambar 5
 Mula-mula kita nyatakan arus ini sebagai jumlah arus
alami dan arus paksaan.
i(t) = in + if
 Tanggapan alamiah dianalisis ketika rangkaian tanpa
sumber (sumber dihubung singkat atau saat t < 0),
maka didapatkan
in  Ae

Rt
L
 Tanggapan paksaan tergantung pd sifat fungsi
pemaksa itu sendiri. Tanggapan paksaan haruslah
positif untuk semua harga waktu yang positif (t> 0).
 Sehingga arus paksaan if adalah:
V
if 
R
 Jadi tanggapan total arus adalah :
Rt

V
L
i (t )  Ae

R
 Untuk mencari nilai A, maka dipakai syarat awal, yaitu
nilai arus saat segera setelah t = 0 yaitu i(0) = 0.
V
0  A
R
 Sehingga
V
A
R
 Maka tangapan totalnya menjadi
V V  RtL
i(t )   e
R R
 Grafik tanggapan arus total
Gambar 6. grafik tanggapan arus total
 Sekarang kita perhatikan rangkaian dibawah ini
Gambar 7.
 Pada gambar 7 diatas terdapat sumber tegangan dc ,
sumber tegangan tangga satuan . Kita tentukan nilai
i(t) untuk semua harga waktu.
 Kita dapat melihat rangkaian disebelah kiri induktor
dengan rangkaian thevenin, sehingga tahanan
thevenin nya adalah rangkaian pararel R = 2 Ohm dan
R = 6 Ohm yaitu Rth = 1,5 Ohm.
 Rangkaian tersbeut mengandung hanya satu elemen
penyimpan energi, yaitu induktor sehingga respon
alamiahnya adalah sebuah eksponensial negatif.
in  Ae
 Rt
L
 Ae

1, 5t
3
 Ae
t

2
……….. t > 0
 Respon arus paksaan if haruslah arus yang dihasilkan
sebuah tegangan konstan sebesar 100 Volt, induktor
berlaku seperti hubungan pendek sehingga rangkaian
menjadi
Jadi tanggapan arus
paksaannya adl
100
if 
 50
2
 Jadi tanggapan total arusnya adalah
i(t )  i f  in
i(t )  50  Ae 0,5t
t >0
 Untuk menghitung A, kita harus mendapatkan harga
awal arus induktor sebelum t = 0, yaitu rangkaian
menjadi
 i(t) = 50 : 2 = 25 ampere
t < 0
 Dari harga i(0) = 25 ampere, kita dapat mencari nilai
A yaitu
25  50  Ae 0
25 = 50 + A
A = -25
 Maka arus total menjadi :
i(t )  50  25e 0,5t
t > 0
Grafik tanggapan lengkap untuk semua waktu t seperti
diperlihatkan pada Gambar dibawah ini.
Tanggapan alamiah bertugas menghubungkan
tanggapan untuk t < 0 dengan tanggapan paksaan yg
konstan
Gambar 8. Grafik tanggapan lengkap semua t
 Tanggapan untuk Rangkaian RC
Perhatikan rangkaian RC pada gambar 9 di bawah ini.
Gambar 9. Rangkaian RC
 Tanggapan lengkap rangkaian RC adl sebagai
penjumlahan tanggapan alami dan paksaan.
 Pada t < 0, kontak penghubung berada pada posisi (a)
dalam waktu yg lama sehingga tanggapan alami telah
menurun menjadi amplitudo yg dapat diabaikan, dan
sekarang tinggal tanggapan paksaan dari sumber 120
V.
 Tegangan vc(t) pada t < 0 diakibatkan oleh sumber 120
V konstan sehingga tdk ada arus yg mengalir pada
kapasitor.
 Sehingga vc(0) adalah pembagi tegangan pada tahana
50 Ohm terhadap sumber 120 V.
50
vc(0) 
.120  100
50  10
Karena tegangan kapasitor tdk dapat berubah seketika,
maka tegangan ini berlaku juga pada t = 0+ dan t = 0-.
Kontak penghubung sekarang dilemparkan ke b, dan
tanggapan lengkap adalah :
vc  vc f  vcn
Tanggapan alamiah didapat dengan mengganti sumber 50 v
dg sebuah hubungan pendek untuk menghitung tahanan
ekivalen.
1
Re q 
 24
1
1
1


50 200 60
vcn  Ae

t
Re q .C
 Ae

t
1, 2
Untuk menghitung tanggapan paksaan bila kontak
Penghubung berada pada posisi b, kita tunggu sampai
tegangan dan arus telah berhenti berubah, jadi perlakukanlah kapasitor sebagai rangkaian terbuka.
Maka sekali lagi kita menggunakan pembagi tegangan.
(50)(200) /(50  200)
vcf 
50  20
60  (50)(200) /(50  200)
 Sehingga tanggapan total vc adalah :
vc  20  Ae

t
1, 2
 Untuk mendapatkan nilai A, kita gunakan syarat awal
yaitu vc saat sebelum t = 0. Sehingga :
100 = 20 + A
A = 80.
sehingga tanggapan total vc menjadi :
vc  20  80e

t
1, 2
t>0
 Grafik tanggapan total vc seperti pada gambar di
bawah ini