2.2. Momen Lentur dan Distribusi Tegangan Geser

II. LENTURAN
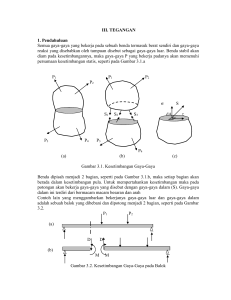
Pembebanan lentur murni yaitu pembebanan lentur, baik akibat gaya
lintang maupun momen bengkok yang tidak terkombinasi dengan gaya
normal maupun momen puntir, ditunjukkan pada Gambar 2.1. Gambar
2.1(a) disebut balok kantilever sedangkan jenis yang lain adalah balokbalok dengan penumpuan elastis sederhana, Gambar 2.1(b). Gaya
dalam yang bekerja pada balok-balok tersebut mungkin akan berupa
tegangan normal dan atau tegangan geser. Bebannya tidak hanya
terbatas pada kopel seperti pada gambar, mungkin juga gaya lintang.
Gambar 2.1. Pembebanan Lentur
Pendekatan yang dilakukan untuk pemecahan masalah ini digunakan
teori balok menurut makanika klasik. Cara ini dikenal dengan
pemecahan pendekatan karena persoalannya dideskripsikan secara pasti
namun kemudian digunakan asumsi-asumsi. Pendekatan lain adalah
penyelesaian menurut teori elastisitas yang dikenal dengan
penyelesaian eksak, karena pada pendekatan ini persoalannya
disederhanakan namun tidak dilakukan asumsi-asumsi.
Untuk
kepentingan praktis penyelesaian pendekatan cukup akurat apabila
balok tersebut cukup panjang, lh, dan relatif jauh, lebih dari h, dari
titik tumpuan atau titik beban terpusat. Untuk balok-balok yang
pendek dan di sekitar titik tumpuan dan titik beban terpusat,
penyelesaian eksak akan memberikan hasil yang lebih akurat. Hal ini
sesuai dengan prinsip Saint Venant, yang pertama kali dikemukakan
oleh seorang insinyur Perancis, Barre de Saint Venant, pada tahun
1855.
2.1. Momen Lentur dan Distribusi Tegangan Normal
Gambar 2.2(a) di bawah menunjukkan sebuah balok sebelum
mendapatkan pembebanan. Gambar 2.2(b) setelah mengalami
perubahan bentuk. Diambil elemen CD sembarang dari balok AB, lalu
diperbesar seperti ditunjukkan pada Gambar 2.2(c).
Gambar 2.2. Pembebanan Lentur
Terlihat bahwa sepanjang bagian
12DC mengalami perpendekan
sehingga titik yang tadinya di 1 berpindah ke 1’, sedangkan
sepanjang bagian CD34 mengalami perpanjangan yang ditandai dengan
berpindahnya titik 4 ke 4’. Dengan demikian dapat diketahui bahwa
serat-serat sepanjang bagian 12DC mengalami pembebanan tekan,
sedangkan sepanjang bagian DC34 mengalami pembebanan tarik.
Sumbu netral terletak sepanjang titik berat penampang lintang
sepanjang batang.
Untuk elemen CD yang sangat pendek, maka dapat dipandang sebagai
busur lingkaran sebesar q radial dengan jari-jari r, sehingga:
q=
atau
CD C' D'
C' D'
y
C' D'
y
=
Þ
= 1- Þ
-1 = r
r-y
CD
r
CD
r
C' D'-CD panjang setelah pembebanan - panjang semula
y
=
=CD
r
panjang semula
Sehingga
y
e xx = r
(2.1)
Dengan perkataan lain, besar regangan pada suatu serat berbanding
lurus dengan jarak serat tersebut dari sumbu netral.
Selanjutnya, menurut hukum Hooke, besarnya regangan satu dimensi
adalah
y
s xx
=
=
e xx
E
r
Sehingga
y
=
E
s xx
(2.2)
r
dengan:
sxx = tegangan yang terjadi (N/mm2, MPa)
E = modulus Young, modulus elastisit (N/mm2, MPa)
y = jarak serat dari sumbu netral (mm)
r = jari-jari lengkungan (mm)
Karena untuk suatu bengkokan tertentu pada bahan tertentu, E dan r
adalah konstan, maka jelaslah bahwa tegangan pada suatu serat
tertentu merupakan fungsi linier jarak serat tersebut terhadap sumbu
netral. Distribusi tegangan normal sepanjang sumbu y ditunjukkan
pada Gambar 2.2(d).
Sebagian penampang lintang balok diambil elemen sembarang dA yang
berjarak y dari sumbu netral, Gambar 2.2(e). Besar elemen gaya yang
bekerja pada luasan tersebut adalah
dF = sxx . dA
(2.3)
Karena jaraknya terhadap sumbu netral, maka elemen gaya tersebut
menimbulkan elemen momen terhadap sumbu netral sebesar
yö
æ
d M b = y. dF = y. s x . dA = yç - E ÷ dA
è
rø
Sehingga
Karena
maka
E 2
=
Mb
 y .dA
r
(2.4)
 y2 . dA = I
(2.5)
EI
Mb =
r
(2.6)
dengan:Mb = momen bengkok (N.mm)
I = momen lembam linier atau inersia linier (mm4)
r = jari-jari bengkokan (mm)
Dari persamaan (2.6) didapat r =
EI
Mb
, yang kemudian dimasukkan ke
persamaan (2.2) sehingga didapat
s xx = -
Mb . y
I
2.2. Momen Lentur dan Distribusi Tegangan Geser
(2.7)
Gambar 2.3. Elemen Balok yang Mengalami Lenturan
Gaya normal yang bekerja pada elemen yang diarsir pada sisi kiri adalah
F n1 = s xx.dA =  - MI b
.y
dA
(2.8a)
Sedangkan gaya normal pada sisi kanan elemen untuk luasan dan posisi
yang sama akan diperoleh
+d
.y
(2.8b)
b
b
Fn2 =  (σxx + d σxx ). dA = s xx.dA = 
(M
M)
I
dA
Sedangkan gaya geser pada bidang horisontal yang menyebabkan
keseimbangan pada elemen-elemennya adalah
Ft = -t b dx
(2.8c)
Jumlah gaya yang bekerja pada arah mendatar sama dengan nol,
sehingga
(
M b + d M b). y
Mb . y
dA + 
dA - t. b. dx = 0
å Fh = 0 ®  I
I
d Mb . y
t. b. dx = 
dA
I
1 d Mb
t=
. ydA
.

I. b dx
dM b
= Fv
dx
 y. dA = Q
(2.9)
(2.10)
(2.11)
Dengan substitusi persamaan-persamaan (2.8) dan (2.9)
pada persamaan (2.8) akan didapat besarnya tegangan
geser pada serat C’D’ dalam paskal (Pa)
Fv . Q
=
t xy
I. b
(2.12)
dengan:
Fv = jumlah gaya-gaya vertikal yang bekerja pada
elemen
dx (N)
Q = inersia bidang di luar serat dari arah sumbu
netral
terhadap sumbu netral (mm3)
I = inersia penampang lintang balok (mm4)
b = tebal balok (mm)
Untuk penampang lintang berbentuk segi empat dengan
tebal b (mm) dan tinggi h (mm) besar Q adalah
2
h
Q=
2
- 4 y1
8
Q =  y.dA =
2
h
dz =
b/2

-b / 2
-b / 2
- 4 y1
2
z
8
b/2
-b / 2
h
=
2
- 4 y1 æ b b ö
ç + ÷
8
è2 2ø
b/2
æ h/2
ö
1
ç y.dy ÷dz =
y
(
dy
.
dz
)
=

/ 2 ç y ÷ -b/ 2 2
b
è 1
ø
y1
b/2 h/2

2
h/2
b/2
y
2
dz
y1
(
- 4 y )b
h
Q=
2
2
1
8
(2.13)
Dengan substitusi persamaan (2.12) pada persamaan (2.11) akan
didapat besar tegangan geser dalam paskal (Pa) yang bekerja bidang
C’D’D”C” yang berjarak y1 dari sumbu netral, adalah
(
2
Fv . h - 4 y1
2
)
(2.14)
dengan
t xy =
8. I
Fv = jumlah gaya-gaya vertikal yang bekerja pada elemen dx (N)
h = tinggi penampang lintang balok (mm)
y1 = jarak serat dari sumbu netral (mm)
I = inersia penampang lintang (mm4)
Perhatikan persamaan tersebut di atas.
Untuk suatu
penampang lintang tertentu pada panjang balok, besarnya
gaya-gaya vertikal yang bekerja padanya adalah konstan.
Dengan demikian, distribusi tegangan geser pada serat
tertentu pada penampang lintang sepanjang sumbu
vertikalnya, sumbu y, merupakan fungsi parabolik jarak
serat tersebut terhadap sumbu netral yang dinyatakan oleh
2
Fv . hbesarnya tegangan geser3maksimum
y12. Sedangkan
terjadi
Fv
t xy- max =
t xy - max =
pada harga 8æçy11 =
0
yaitu
3,
ö
2 bh
. b. h ÷
è 12
(2.15a)
ø
Þ
2.3. Persoalan-persoalan Khusus
Sedangkan
tegangan geser minimum terjadi bila y = h/2 ,
Kekhususan dalam hal ini adalah konstruksi titik tumpuan 1dan jenis
yaitu
beban. Balok kantilever seperti Gambar 2.1a dan balok di atas dua
tumpuan elastis sederhana seperti Gambar
2.1b
txy-max
= 0merupakan persoalan
yang sering
dijumpai. Sedangkan beban dapat berupa beban terpusat
(2.15b)
atau beban titik, beban merata baik yang konstan maupun yang
variabel, dan momen bengkok.
a. Balok Kantilever
Gambar 2.4 di bawah menunjukkan sebuah balok kantilever dengan
berbagai macam beban.
Gambar 2.4. Balok Kantilever dengan Berbagai Macam Beban
Gaya-gaya F2 dan F3 disamping memberikan beban normal secara
langsung, juga menimbulkan kopel sebesar F2 r2 + F3 r3 yang akan
membengkokkan balok AB. Dengan adanya beberapa beban tersebut,
maka besarnya momen lentur pada sepanjang balok AB dapat dibagi
menjadi lima daerah, yakni daerah AC, CD, DE, EF dan FB.
(2.16a)
0 £ x £ a Þ Mx = F1 .x
a £ x £ b Þ Mx = F1.x - q (x - a){ (x - a)} = F1.x - q ( x-a)
2
2
1
1
2
b £ x £ c Þ Mx = F1 .x - q ( x-a) + F2 r 2 + F3 r 3
2
1
2
1
2
1
(c - a)} + F2 r 2 + F3 r 3 - F4 (x - d )
2
(2.16b)
(2.16c)
c £ x £ d Þ Mx = F1.x - q (c - a){(x - a) - (c - a)} + F2 r 2 + F3 r 3
(2.16d)
d £ x £ l Þ Mx = F1.x - q (c - a){(x - a) -
(2.16.e)
Turunan pertama persamaan-persamaan (2.15a) sampai dengan
(2.15e) di atas berturut-turut adalah
0£ x£ a Þ
a£x£b Þ
b£x£c Þ
c£ x£ d Þ
d£x£l Þ
dM x
= F1
dx
dM x
= F1 - q ( x - a )
dx
dM x
= F1 - q ( x - a )
dx
dM x
= F1 - q ( c - a )
dx
dM x
= F1 - q ( c - a ) - F4
dx
(2.17a)
(2.17b)
(2.17c)
(2.17d)
(2.17.e)
Selanjutnya perhatikan persamaan (2.7)
dan (2.13).
Ternyata bahwa distrubusi tegangan normal menurut
persamaan (2.7) dipengaruhi oleh torsi akibat beban F2
dan F3. Sedangkan distribusi tegangan geser menurut
persamaan (2.13) tidak tergantung pada adanya kopel
akibat gaya F2 dan F3 tersebut.
b. Balok Di atas Dua Tumpuan Elastis Sederhana
Dengan memendang reaksi titik tumpuan sebagai gaya aksi dan bagian
tengah balok dengan sudut lenturan sama dengan nol sebagai tumpuan
jepit, bagian balok yang akan dicari distribusi gaya normal dan gaya
gesernya dari balok di atas dua tumpuan elastis sederhana dapat
diperlakukan sebagai balok kantilever, karena perilakunya yang sama
dalam pembebanan. Jadi perhitungan momen adalah sama dengan yang
telah dilakukan terhadap balok kantilever di atas.
2.4. Pembebanan Kombinasi Normal dan Lentur
Dalam hal ini suatu batang dismaping menderita beban tarik atau tekan
langsung, juga menderita beban lentur.
Pada Gambar 2.5a ditunjukkan bahwa batang ABCD mendapat beban F1
dan F2 yang tidak sama besarnya pada arah sumbu x. Gaya-gaya F1
dan F2 disebut gaya normal. Penampang lintang batang ABCD
ditunjukkan pada Gambar 2.5b.
Gambar 2.5. Pembebanan Kombinasi
Akibat selisih besar F1 dan F2 maka batang ABCD akan menderita
tegangan normal langsung yang besarnya
(2.17)
å Fv
s xx-1 =
dengan:
sA
xx-1 = tegangan normal langsung (MPa)
SFx = jumlah gaya-gaya horisontal, searah sumbu x (N)
A = luas penampang lintang balok (mm2)
Grafik
distribusi
tegangan
normal
Gambar
2.5c
menunjukkan distribusi tegangan normal langsung pada
setiap serat pada penampang lintangnya.
Karena gaya-gaya F1 dan F2 bekerja berlawanan arah dan
adanya jarak terhadap sumbu netral, maka akan timbul
kopel sebesar
Mb = Mx = F1 . a + F2 . b
(2.18)
Akibat momen lentur tersebut, serat pada sisi AB akan
menerima tarikan, sedangkan pada sisi CD akan menrima
tekananMatau
desakan. Menurut persamaan (2.7) besarnya
b . y1
s xx - AB =pada serat AB dan CD berturut-turut adalah(2.19a)
beban
I
s xx - CD =
M b . y2
I
(2.19b)
Distribusi tegangan yang diberikan oleh persamaan-persamaan (2.19a)
dan (2.19b) digambarkan dalam grafik pada Gambar 2.5d.
Untuk menghitung tegangan total yang terjadi pada setiap serat pada
suatu penampang lintangnya dapat dilakukan dengan menjumlahkan
grafik tegangan Gambar 2.5c dan Gambar 2.5d. Hasil ini ditunjukkan
pada Gambar 2.5e.
Dalam perencanaan suatu konstruksi, diambil tegangan total maksimum
terbesar yang terjadi antara serat-serat terluarnya.
Contoh Soal: Sebuah kuda-kuda rumah dibuat dengan rangka kaku bentuk simetri.
Panjang bentangannya 5,6 m dan tingginya 2,1 m. Gaya bekerja pada bubungan
atap sebesar 1 kN. Penampang lintang berbentuk empat persegi panjang dengan
tebal 8 cm dan tinggi 12 cm. Hitunglah tegangan maksimum yang terjadi.
Penyelesaian:
F = 1 kN = 1000 N smax = ?
Konstruksi simetri, sehingga RA = RB = R/2 = 500 N.
Dengan dalil Phytagoras, didapat panjang AC = 3,5 m.
RAh = RA cos a = 500 (2,1/3,5) = 300 N.
Mb maksimum terjadi di C yang besarnya Mb = RA . 2,8 = 1400 N.m = 140000 N.cm.
Akibat beban normal, terjadi tegangan normal langsung sebesar
sxx-1 = RAh / A = 300 / (12 . 8) = 3,125 N / cm2
Akibat lenturan, terjadi tegangan normal tak langsung sebesar
sxx-2 = Mb.y / I dengan y = h / 2 = 6 cm.
I = (1 / 12) b h3 = (1 / 12) . 8 . 123 = 1152 cm4.
sehingga
sxx-2 = 140000 . 6 / 1152 = 729 N/cm2.
Dengan demikian, tegangan maksimum berupa tegangan desak pada serat bagian atas
yang besarnya
sxx-max = sxx-1 + sxx-2 = 732,125 N/cm2.
2.5. Pusat Geser
Pusat geser, S pada Gambar 2.6 pada halaman depan,
adalah titik yang dilewati garis kerja resultan gaya-gaya
geser dalam. Agat tidak terjadi puntiran maka resultan
gaya-gaya luar juga juga harus dilewatkan titik tersebut.
Untuk baja profil pada umumnya b dan h jauh lebih
besar dari t1 maupun t2 sehingga distribusi tegangan
geser pada bagian hirosontal (flange) dan pada bagian
vertikal (web) dari penampang lintangnya seperti yang
ditunjukkan pada Gambar 2.6(b). Pada bagian horisontal,
tegangan geser maksimumnya akan terjadi pada
b. h
F .dengan
pertemuannya
bagian vertikal, yang besarnya
t1 =
I
adalah
(2.20a)
Gambar 2.7. Lenturan Murni Pada Profil Kanal
dengan
t1 = tegangan geser maksimum pada penampang bagian
horisontal
(MPa)
Fv = jumlah gaya-gaya vertikal yang bekerja pada
penampang
tersebut (mm2)
b = lebar penampang lintang (mm)
h = setengah tinggi penampang lintang (mm)
I = inersia penampang lintang (mm4)
Tegangan tersebut akan memberikan total gaya dalam pada bagian
horisontal bagian atas F1 seperti ditunjukkan pada Gambar 2.6(c),
yang besarnya
2
1
F . b . h. t1
F1 = t1 . b. t1 =
2
2. I
(2.20b)
dengan t1 adalah tebal penampang lintang bagian horisontal (mm).
Dalam keadaan seimbang, jumlah gaya-gaya horisontal harus sama
dengan nol, maka pada bagian horisontal bawah akan timbul gaya
horisontal F3 yang sama besar dengan F1 namun dengan arah yang
berlawanan, sehingga secara matematis
F1 = -F3
(2.20c)
Pada ujung-ujung bagian vertikal akan dibangkitkan tegangan geser
sebesar
F . b.h .t1
t2 =
I. t 2
(2.21a)
dengan t2 adalah tebal penampang lintang bagian vertikal
(mm). Tegangan tersebut sepanjang sumbu y berdistribusi
secara parabolik sepert ditunjukkan pada Gambar 2.6(b).
Total gaya akibat tegangan tersebut pada luasan
penampang lintang bagian vertikalnya adalah F2 seperti
pada Gambar 2.6(c) yang besarnya dapat dicari dengan
0 Þ F2 = F
å F v =keseimbangan
prinsip
gaya-gaya vertikal
= 0 Þ - F. e + F1 .2h = 0
å M A (2.21b)
F1 .2h mensyaratkan
Keseimbangan
atau
e =rotasi
F
2
(2.22)
2
b h t1
e=
I
Substitusi persamaan
(2.20b) pada persamaan (2.22) akan
Sedangkan besarnya I = 1 . t 2 .( 2h) 3 + 2. 1 b t13 + 2b t1 . h 2 , namun karena t1
12
12
didapat
(2.23)
{
}
1
jauh lebih kecil dari b maupun h maka harga 12 b t13 sangat kecil dan
dapat diabaikan terhadap harga I secara keseluruhan, sehingga
I=
2
. t 2 . h 3 + 2 b t1 . h 2
3
(2.24)
Substitusi persamaan (2.24) pada persamaan (2.23) akan diperoleh
2
2
2 b h t1
e=
3 h. t 2 + 3b. t1
(2.25)
2.6. Arus Geser
Arus geser pada lenturan dapat didefinisikan sebagai hasil perkalian
antara tegangan geser, t, dengan tebal dinding pada balok
berpenampang ‘profil’, t, yang mendapatkan pembebanan lentur. Jadi,
besarnya arus geser dalam N/mm pada prifil adalah adalah
q =t.t
(2.26)
dengan t adalah tegangan geser (Pa, N/mm2)
t adalah tebal dinding (m, mm).
Gambar 2.8. Arus Geser
Besarnya arus geser dapat dicari dengan penerapan prinsip
keseimbangan gaya-gaya pada arah horisontal pada Gambar 2.8b.
S Fh = 0 Þ – H – F + H’ = 0
atau
F = H’ - H
(2.27)
F = q dx
(2.28a)
(2.28b)
H =  s xx. dA = 
Mb .y
. dA
I
H =  (s xx + d s xx). dA = 
(2.28c)
( M b + d M b).y .dA
I
Dengan substitusi persamaan-persamaan (2.28a), (2.28b)
dan (2.28c) pada persamaan (2.27) akan diperoleh
q . dx = 
( M b + d M b) - M b .y.dA = 1
I
atau
q=
1 dM b
 y.dA
I dx
dengan dMb = Fv
dx
pada penampang
I
 dM b . ydA
(2.29)
adalah jumlah gaya-gaya vertikal
tersebut (N)
 y . dA = Q adalah momen bidang di luar serat itu
terhadap sumbu netral (m3)
Dengan demikian, besarnya arus geser di titik A adalah
q = t.t =
Fv . Q
I
(2.30)
Gambar 2.9. Distribusi Arus Geser pada Berbagai Bentuk
Penampang
Contoh Soal: Balok pipa berpenampang segi empat dengan
ukuran
seperti pada Gambar 2.10(a) menerima beban
geser sebesar 10
kN. Tentukan distribusi arus geser pada
penampang tersebut !
Gambar 2.10. Profil Pipa Segi Empat dengan Beban Lentur
(Ukuran dalam milimeter)
Penyelesaian:
Karena terdapat dua sumbu simetri, maka sumbu netral akan
melewati perpotongan kedua sumbu simetri tersebut. Jadi hanya arus
geser di titik- titik B, C dan D saja yang perlu dicari, sedangkan
distribusinya linier pada bagian horisontal dan parabolik pada bagian
yang vertikal.
I = (1/12)(60.803 - 40.603) = 1 840 000 mm4
Di titik B:
AB = 0 sehingga QB Þ
qB =
Fv QB
=0
I
Di titik C:
QC = y AC = 35 (50 x 10) = 17 500 mm3
qC =
Fv QB 10.000x17500
=
= 99,11
I
1840000
(N/mm)
Di titik D:
QD = S ( y AD ) = 20 (40 x 10) + 35 (40 x 10) + 20 (40 x 10) = 30 000 (mm3)
qD =
Fv QD 10.000x30000
=
= 163
I
1840000
(N/mm)