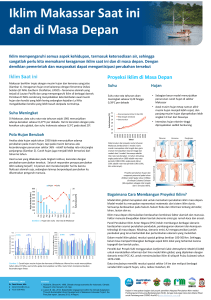
Tabel 1.1 Hasil estimasi parameter regresi kuantil

PENGUJIAN HIPOTESIS PADA REGRESI
KUANTIL
Nurwahida Astari, Amran, Andi Kresna Jaya
Departemen Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin
E-mail: nurwahida.astari95yahoo.co.id
Abstrak
Umumnya, pengujian hipotesis pada analisis regresi didasarkan pada asumsi error
berdistribusi normal dengan 𝜇 = 0 dan variansi 𝜎 2 . Namun, asumsi error berdistribusi
normal tidak dipenuhi pada kelompok data dengan bentuk distribusi tidak simetris. Salah
satu metode analisis untuk data yang berdistribusi tidak simetris adalah regresi kuantil.
Pengujian hipotesis pada regresi kuantil menjadi suatu masalah penting yang perlu diatasi.
Tugas akhir ini membahas tentang pengujian hipotesis pada regresi kuantil menggunakan
uji Wald. Estimasi parameter menggunakan metode interior point dengan algoritma
Frisch-Newton. Ditunjukkan bahwa distribusi asimtotik estimator berdistribusi normal
(0, 𝑊0 ). Dari distribusi asimtotik tersebut diperoleh fungsi sparsity. Rumusan fungsi
sparsity digunakan untuk mengkonstruksi statistik uji Wald yang berdistribusi chi-square
dengan derajat bebas 𝑛. Aplikasi pengujian hipotesis pada regresi kuantil menggunakan
kuantil atas menunjukkan bahwa Sea Surface Temperature (SST) Niño 3.4 memberikan
pengaruh yang signifikan terhadap curah hujan di Kota Makassar pada kuantil 0.75, 0.80,
0.85, 0.90, dan 0.95.
Kata Kunci:
Regresi Kuantil, Interior Point, Asimtotik Distribusi Normal, Fungsi
Sparsity, Uji Wald, Curah Hujan, SST Niño 3.4.
Pendahuluan
Analisis regresi dalam ilmu statistika merupakan salah satu metode statistik
yang digunakan untuk melihat apakah ada hubungan yakni sebab dan akibat antara
dua atau lebih variabel. Variabel dibagi menjadi dua jenis yaitu variabel terikat dan
variable bebas. Analisis regresi memerlukan suatu metode untuk estimasi parameter
yang memenuhi sifat Best Liniear Unbiased Estimator (BLUE). Salah satu metode
estimasi yang sering digunakan adalah Ordinary Least Square (OLS). Analisis
regresi menggunakan metode OLS berdasarkan pada fungsi mean. Perkembangan
metode estimasi parameter model dengan data berdistribusi tidak simetris dimulai
dengan metode Least Absolute Deviation (LAD) dan dikenal sebagai regresi kuantil
median. Nilai estimasi parameter dengan menggunakan metode LAD dapat
diperoleh dengan meminimumkan jumlah nilai mutlak dari error. Selain regresi
kuantil median dikenal juga regresi kuantil.
Regresi kuantil adalah salah satu metode regresi dengan memisahkan atau
membagi data menjadi kuantil-kuantil tertentu dimana diduga terdapat perbedaan
nilai estimasi. Regresi kuantil pertama kali diperkenalkan oleh Koenker dan Basset
(1978). Rahmawati dkk (2011) meneliti regresi kuantil mengenai studi kasus pada
data suhu harian. Navianti (2014) membahas mengenai regresi kuantil untuk
pemodelan tingkat pengangguran terbuka di Indonesia. Rahmawati dkk (2011)
hanya berfokus pada estimasi parameter regresi kuantil dan Navianti (2014)
berfokus pada selang kepercayaan pada regresi kuantil.
Regresi kuantil sangat berguna untuk data dengan distribusi tidak simetris,
dalam bidang meteorologi dapat diterapkan pada data curah hujan, temperatur, dan
perubahan iklim. Data curah hujan merupakan data musiman, sehingga pada waktu
tertentu (Desember, Januari, Februari) terjadi hujan lebat. Kejadian Hujan lebat
dapat dimodelkan dengan menggunakan analisis regresi kuantil bagian atas,
khususnya untuk nilai ekstrem. Kombinasi dari setiap nilai kuantil dapat
menjelaskan pola keseluruhan data sehingga bermanfaat untuk menganalisa bagian
tertentu dari sebaran bersyarat.
Pengujian hipotesis merupakan hal yang penting dalam tahapan analisis
regresi. Pengujian hipotesis pada analisis regresi didasarkan pada asumsi error
berdistribusi normal dengan 𝜇 = 0 dan variansi 𝜎 2 dengan data yang berdistribusi
simetris. Asumsi error tersebut umumnya tidak dipenuhi pada data kuantil atas
yang berdistribusi tidak simetris. Berdasarkan asumsi tersebut penulis tertarik untuk
membahas “Pengujian Hipotesis pada Regresi Kuantil”.
Regresi Kuantil
Misalnya 𝑌 merupakan suatu variabel acak dengan suatu fungsi distribusi
𝐹𝑌 dan 𝜏 merupakan konstanta dimana 0 < 𝜏 < 1. Kuantil ke- 𝜏 dari 𝐹𝑌 ,
dinotasikan sebagai 𝑞𝑌 (𝜏) merupakan solusi untuk 𝐹𝑌 (𝑞) = 𝜏, adalah sebagai
berikut:
𝑞𝑦 (𝜏) ≔ 𝐹𝑦−1 (𝜏) = inf{𝑦 ∶ 𝐹𝑌 (𝑦) ≥ 𝜏}.
Seperti halnya dengan suatu metode OLS yang digunakan sebagai meminimumkan
jumlah kuadrat error (sisaan) untuk menentukan suatu nilai parameter 𝛽, maka
dalam analisis regresi kuantil, kuantil ke- 𝜏 dari 𝐹𝑌 dapat diperoleh dengan
meminimumkan suatu fungsi berikut ini terhadap 𝑞:
|𝑦 − 𝑞|𝑑𝐹𝑌 (𝑦) + (1 − 𝜏) ∫
𝜏∫
𝑦>𝑞
= 𝜏∫
|𝑦 − 𝑞|𝑑𝐹𝑌 (𝑦)
𝑦<𝑞
(𝑦 − 𝑞)𝑑𝐹𝑌 (𝑦) − (1 − 𝜏) ∫
𝑦>𝑞
(𝑦 − 𝑞)𝑑𝐹𝑌 (𝑦).
(1)
𝑦<𝑞
Dengan meminimumkan fungsi persamaan (1), dapat diperoleh persamaan berikut
ini:
0 = −𝜏 ∫
𝑑𝐹𝑌 (𝑦) + (1 − 𝜏) ∫
𝑦>𝑞
𝑑𝐹𝑌 (𝑦)
𝑦<𝑞
0 = −𝜏[1 − 𝐹𝑌 (𝑞)] + (1 − 𝜏)𝐹𝑌 (𝑞)
0 = −𝜏 + 𝐹𝑌 (𝑞)
sehingga diperoleh:
𝜏 = 𝐹𝑌 (𝑞),
sehingga persamaan (2) merupakan kuantil ke- 𝜏 adalah solusi dari 𝐹𝑌 .
(2)
Misalkan 𝑌 sebagai suatu fungsi dari 𝑋 yang telah diketahui, yang memiliki
peluang yaitu 𝐹𝑌|𝑋 (𝑦), maka kuantil ke- 𝜏 dari fungsi tersebut dapat dituliskan
−1
(𝜏). 𝑄𝑌|𝑋 (𝜏) ini merupakan suatu fungsi dari 𝑋 dan dapat
sebagai 𝑄𝑌|𝑋 (𝜏) ≔ 𝐹𝑌|𝑋
diselesaikan dengan persamaan berikut ini:
min [𝜏 ∫ |𝑦 − 𝑞|𝑑𝐹𝑦 (𝑦) + (1 − 𝜏) ∫ |𝑦 − 𝑞|𝑑𝐹𝑦 (𝑦)].
𝑞
𝑦>𝑞
(3)
𝑦<𝑞
Jika 𝑄𝑌|𝑋 (𝜏) adalah fungsi linier 𝑿𝜷, dengan vektor parameter 𝛽 yang tidak
diketahui, sehingga persamaan (3) menjadi:
|𝑦 − 𝑋𝛽|𝑑𝐹𝑌 (𝑦) + (1 − 𝜏) ∫
min [𝜏 ∫
𝛽
𝑦>𝑋𝛽
|𝑦 − 𝑋𝛽|𝑑𝐹𝑌 (𝑦)] .
(4)
𝑦<𝑋𝛽
Solusi dari persamaan (4) ini dinotasikan sebagai 𝛽0 dan kuantil 𝑌 (sebagai fungsi
dari 𝑋) ke- 𝜏 adalah 𝑄𝑌|𝑋 (𝜏) = 𝑋𝛽0 (Kuan, 2007).
𝑄𝑌|𝑋 (𝜏) = 𝑥𝑡 𝛽 adalah kuantil ke-𝜏 (0 < 𝜏 < 1) yang nilai 𝑦 tergantung
terhadap 𝑥𝑡 . Suatu nilai estimasi terhadap 𝛽 dari regresi kuantil ke-𝜏 diperoleh
dengan meminimumkan jumlah nilai mutlak dari error dengan pembobot 𝜏 untuk
error positif dan pembobot (1 − 𝜏) untuk error negatif adalah:
𝛽̂ (𝜏) = arg min {𝜏 ∑ |𝑦𝑡 − 𝑥𝑡 𝛽| + (1 − 𝜏) ∑ |𝑦𝑡 − 𝑥𝑡 𝛽|}
𝛽
𝑡:𝑦𝑡 ≥𝑥𝑡
(5)
𝑡:𝑦𝑡 <𝑥𝑡
atau
𝛽̂ (𝜏) = arg min ∑
𝛽
𝑛
𝜌𝜏 (𝑢𝑖 )
𝑖=1
(6)
untuk:
𝜏𝑢𝑖
𝜌𝜏 (𝑢𝑖 ) = {
(𝜏 − 1)𝑢𝑖
jika 𝑢𝑖 ≥ 0
jika 𝑢𝑖 < 0
Solusi dari persamaan (5) atau (6) tidak dapat diperoleh secara analitik,
melainkan dikerjakan secara numerik, seperti metode simplex, metode interior
point, atau metode smoothing.
Pengujian Hipotesis
Analisis regresi kuantil diterapkan pada sampel yang berukuran besar, maka
parameter regresi kuantil menggunakan uji Wald. Asumsi hipotesis linier adalah
𝑹𝛽𝜏 = 𝒓, dimana 𝑹 adalah matriks dengan full row rank berukuran 𝑞 × 𝑘, dan 𝒓
adalah vektor berukuran 𝑞 × 1 pada nilai hipotesis.
Rumusan hipotesis yang digunakan dalam penelitian ini adalah sebagai berikut:
𝐻0 : 𝛽 = 0
𝐻1 : 𝛽 ≠ 0
A. Inferensi Asimtotik pada Regresi Kuantil
Dalam regresi kuantil terdapat fungsi kuantil bersyarat ke-𝜏 yang
mempertimbangkan estimasi 𝛽(𝜏), sehingga diperoleh solusi pada persamaan (6)
atau dinyatakan pada persamaan (7):
𝛽̂ (𝜏) = arg min ∑
𝛽
𝑛
𝜌𝜏 (𝑌𝑖 − 𝑋𝑖 𝛽).
(7)
𝑖=1
Beberapa kondisi yang digunakan Newey dan McFadden (1994) terhadap
teorema asimtotik normal sebagai berikut:
𝑛
1
−1
(8)
∑ 𝑋𝑖 {1[𝑌𝑖 ≤ 𝑋𝛽(𝜏)] − 𝜏} + 𝑂𝑝 (1)
√𝑛[𝛽̂ (𝜏) − 𝛽(𝜏)] = 𝑀0
√𝑛 𝑖=1
Berdasarkan persamaan (8) 𝑀0 adalah Hessian terhadap limit fungsi loss, dan
1
𝑛
𝑑
∑ 𝑋𝑖 {1[𝑌𝑖 ≤ 𝑋𝛽(𝜏)] − 𝜏} → 𝒩(0, 𝑉0 )
√𝑛 𝑖=1
dengan:
𝑉0 = 𝐸({1[𝑌𝑖 ≤ 𝑋𝛽(𝜏)] − 𝜏}2 𝑋𝑖 𝑋𝑖′ ) = 𝜏(1 − 𝜏)𝐸(𝑋 ′ 𝑋𝑖 ).
Perhatikan bahwa asumsi linier pada kuantil bersyarat adalah dinyatakan dalam
persamaan (9) dan (10):
𝑑
(9)
√𝑛[𝛽̂ (𝜏) − 𝛽(𝜏)] → 𝒩(0, 𝑊0 )
dimana:
𝜏(1 − 𝜏)
[𝐸(𝑋𝑖′ 𝑋𝑖 )]−1 .
𝑊0 =
(10)
2
−1
𝑓(𝐹 (𝜏))
B. Menentukan Nilai Statistik Uji
̂𝝉
Uji Wald digunakan pada regresi kuantil untuk mengecek apakah 𝑹𝜷
signifikan terhadap hipotesis nilai 𝒓. Asumsi bahwa estimasi konsisten lemah untuk
−1 (𝜏)). Sehingga dari persamaan (7) diperoleh
𝑓(𝐹 −1 (𝜏)) dinotasikan dengan 𝑓(𝐹̂
hipotesis nol seperti berikut ini:
𝐴
𝜏(1 − 𝜏)
̂
[𝐸(𝑋𝑖′ 𝑋𝑖 )]−1 )
√𝑛[𝛽 (𝜏) − 𝛽(𝜏)] ~ 𝒩 (0,
2
−1
𝑓(𝐹 (𝜏))
−1 (𝜏))
𝑓(𝐹
> 0 memiliki kepadatan positif dimana 𝐹 −1 (𝜏) = 𝑄(𝜏), dengan
parameter skala
𝜏(1−𝜏)
𝑓(𝐹−1 (𝜏))
2
menjadi fungsi 𝑠(𝜏) =
1
𝑓(𝐹 −1 (𝜏))
2
yang disebut sebagai
fungsi sparsity. Parzen (1979) menyatakan bahawa fungsi sparsity adalah fungsi
kepadatan kuantil. Nilai 𝑓(𝐹 −1 (𝜏)) tidak diketahui dan harus diestimasi. Estimasi
telah diusulkan Siddiqui (1960) dalam buku Davino dkk (2014) menyatakan bahwa:
1
𝑠(𝜏) =
−1
𝑓(𝐹 (𝜏))
(11)
−1 (𝜏
𝐹
+ ℎ) − 𝐹 −1 (𝜏 − ℎ)
=
2ℎ
Bandwidth ℎ dari fungsi 𝐹 harus didefinisikan. Koenker dan Machado (1999)
menyarankan menggunakan bandwidth:
ℎ=
1
1 2 1.5𝜙 4 (Φ −1 (𝜏)) 3
𝑛 −3 𝓏 3 [
]
(2Φ−1 (𝜏)2 + 1)
(12)
Berdasarkan teorema Slutsky dan sifat distribusi normal, mengalikan 𝑹 pada
distribusi maka diperoleh:
𝐴
̂
̂
(𝜏)
𝑹√𝑛[𝛽
− 𝛽(𝜏)] = √𝑛(𝑹𝛽(𝜏) − 𝑟) ~ 𝒩(0, 𝑹𝑾𝟎 𝑹′ ).
Dengan hukum bilangan besar lemah, 𝑀𝑛 = 𝑛−1 ∑𝑛𝑖=1 𝒙′𝒊 𝒙𝒊 konsisten terhadap
𝐸(𝑋𝑖′ 𝑋𝑖 ). Estimasi konsisten lemah untuk 𝑊0 adalah:
𝜏(1 − 𝜏)
̂0 =
[𝑀𝑛 ]−1
𝑊
2
−1
𝑓(𝐹 (𝜏))
atau:
̂0 =
𝑊
𝜏(1 − 𝜏)
𝑓(𝐹 −1 (𝜏))
𝑛
2 [𝑛
−1
−1
∑ 𝒙′𝒊 𝒙𝒊 ]
𝑖=1
(13)
sehingga:
1
𝐴
−
2
̂
̂
Γ𝜏 √𝑛(𝑹𝛽(𝜏) − 𝑟) ~ 𝒩(0, 𝑰𝑞 )
1
̂ 𝟎 𝑹′ .
dimana Γ̂ −2 = 𝑹𝑾
1
̂ 𝝉 − 𝒓) merupakan vektor berdistribusi normal. Hasil kali dalam
Γ̂ −2 (𝑹𝜷
antara vektor tersebut sehingga diperoleh statistik uji Wald berikut ini:
𝐴
1
̂ 𝝉 − 𝒓)′ Γ̂ −2 (𝑹𝜷
̂ 𝝉 − 𝒓) ~ 𝜒 2 (𝑛)
(14)
𝒲𝑛 (𝜏) = 𝑛(𝑹𝜷
C. Kriteria Penerimaan dan Penolakan 𝐻0
Jika nilai 𝒲𝑛 (𝜏) ≥ nilai tabel chi-square maka 𝐻0 ditolak
Jika nilai 𝒲𝑛 (𝜏) < nilai tabel chi-square maka 𝐻0 tidak ditolak
Aplikasi Pengujian Hipotesis Pada Regresi Kuantil
Data yang digunakan berupa data curah hujan bulanan dan Sea Surface
Temperature (SST) Niño 3.4. Data curah hujan diperoleh dari BMKG Maros yaitu
data curah hujan Stasiun Meteorologi Hasanuddin Makassar periode Januari 1983September 2015. Data SST Niño 3.4 diperoleh dari internet
http://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino34/. Program komputer
yang digunakan untuk mendukung proses penelitian ini adalah program RStudio.
Berdasarkan fungsi kuantil 𝜏 ∈ [0.1] dapat didekati dalam bentuk fungsi
distribusi empiris. Grafik fungsi distribusi empiris adalah sebagai berikut:
Gambar (a) Fungsi Distribusi Empiris
𝐹𝑦 (𝑌)
Gambar (b) Fungsi Distribusi
Empiris 𝑄𝑌 (𝜏)
Berdasarkan gambar (b) dapat disimpulkan bahwa 𝑄𝑌 (0.75) = 405, yang
berarti pada data curah hujan nilai kuantil 0.75 berada disekitaran 405, kuantil 0.80
berada disekitaran 493, kuantil 0.85 berada disekitaran 552, kuantil 0.90 berada
disekitaran 687, dan kuantil 0.95 berada disekitaran 863.
Tabel 1.1 Hasil estimasi parameter regresi kuantil
Kuantil
0.75
0.80
0.85
0.90
0.95
Sumber: hasil olah data
Intercept (𝛽0 )
403.8846
481.7586
533.6131
643.8378
824.8028
Kemiringan (𝛽1 )
−113.4615
−117.2414
−98.0926
−121.6216
−64.6789
Nilai estimasi parameter 𝛽0 berbanding lurus dengan kuantil dalam hal ini
semakin besar kuantil yang dipilih, maka nilai estimasi parameter 𝛽0 meningkat.
Persamaan regresi untuk kuantil 75%, 80%, 85%, 90%, dan 95% adalah sebagai
berikut:
𝑌75% = 403.8846 − 113.4615𝑋
𝑌80% = 481.7586 − 117.2414𝑋
𝑌85% = 533.6131 − 98.0926𝑋
𝑌90% = 643.8378 − 121.6216𝑋
𝑌95% = 824.8028 − 64.6789𝑋
Selang kepercayaan estimasi parameter 𝛽0 dan 𝛽1 menggunakan 𝛼 = 0.05 untuk
kelima kuantil atas adalah sebagai berikut:
Tabel 1. 2 Selang kepercayaan terhadap estimasi parameter
Kuantil
𝛽0
75%
354.8393 − 451.5338
80%
430.1285 − 522.6401
85%
512.1712 − 610.0504
90%
609.2118 − 739.2684
95%
772.1026 − 917.2122
Sumber: hasil olah data
𝛽1
−144.9374 − (−55.1881)
−145.5004 − (−77.0079)
−151.6838 − (−76.6799)
−146.3982 − (−68.4706)
−175.0718 − 7.7018
Gambar (c) Plot estimasi parameter regresi kuanti pada kuantil atas
Nilai bandwidth berdasarkan pada persamaan (12) adalah:
Tabel 1. 3 Nilai bandwidth berdasarkan data menggunakan program RStudio.
Kuantil
0.75
ℎ
0.0919
Sumber: hasil olah data
0.80
0.0781
0.85
0.0633
0.90
0.0472
0.95
0.0290
Nilai fungsi sparsity berdasarkan persamaan (4.10) pada kuantil 0.75, 0.80, 0.85,
0.90, dan 0.95 adalah sebagai berikut:
Kuantil 0.75 adalah 7.4715 × 10−4
Kuantil 0.80 adalah 5.6522 × 10−4
Kuantil 0.85 adalah 4.6520 × 10−4
Kuantil 0.90 adalah 3.2218 × 10−4
Kuantil 0.95 adalah 2.1887 × 10−4
̂0 pada kuantil
Berdasarkan persamaan (13) nilai estimasi konsisten lemah untuk 𝑊
0.75, 0.80, 0.85, 0.90, dan 0.95 adalah sebagai berikut:
330005.1055
Kuantil 0.75 adalah [
13200.2042
13200.2042
]
435606.7392
492064.9827
Kuantil 0.80 adalah [
19682.5993
19682.5993
]
649525.7771
578849.1751
Kuantil 0.85 adalah [
23153.9670
23153.9670
]
764080.9112
851878.6127
Kuantil 0.90 adalah [
34075.1445
34075.1445
]
1124479.7688
974214.0531
Kuantil 0.95 adalah [
38968.5621
38968.5621
]
1285962.5501
Menentukan nilai statistik uji pada regresi kuantil menggunakan uji Wald
berdasarkan persamaan (14) maka nilai uji Wald pada kuantil 0.75, 0.80, 0.85, 0.90,
0.95 adalah sebagai berikut:
𝒲99 (0.75) = 5.7647 × 1012
𝒲79 (0.80) = 9.5518 × 1012
𝒲59 (0.85) = 1.0015 × 1013
𝒲39 (0.90) = 1.4213 × 1013
𝒲20 (0.95) = 1.3280 × 1013
Penerimaan dan Penolakan 𝐻0
𝒲99 (0.75) ≥ 𝜒 2 (99) atau 5.7647 × 1012 ≥ 123.2252
𝒲79 (0.80) ≥ 𝜒 2 (79) atau 9.5518 × 1012 ≥ 100.7486
𝒲59 (0.85) ≥ 𝜒 2 (59) atau 1.0015 × 1013 ≥ 77.9305
𝒲39 (0.90) ≥ 𝜒 2 (39) atau 1.4213 × 1013 ≥ 54.5722
𝒲20 (0.95) ≥ 𝜒 2 (20) atau 1.3280 × 1013 ≥ 31.4104
Kesimpulan
Untuk mendapatkan statistik uji Wald perlu ditunjukkan bahwa distribusi
asimtotik estimator berdistribusi normal (0, 𝑊0 ). Dari distribusi asimtotik tersebut
diperoleh fungsi sparsity. Rumusan fungsi sparsity digunakan untuk
mengkonstruksi statistik uji Wald yang berdistribusi chi-square dengan derajat
bebas 𝑛. Pengaplikasian pengujian hipotesis pada regresi kuantil menunjukkan
bahwa SST Niño 3.4 memberi pengaruh yang signifikan terhadap curah hujan
ekstrem di Kota Makassar.
Daftar Pustaka
Davino, C., Furno, M., & Vistocco, D. (2014). Quantile Regression Theory and
Applications. Wiley.
Koenker, R., & Bassett, Jr., G. (1978). Regression quantile. Econometrica. 46; 3350.
Kuan, C.-M. (2007). An Introduction To Quantile Regression. Econometrica.
Institute of Economics, Academia Sinica.
Navianti, D. R. (2014). Regresi Kuantil Untuk Pemodelan Tingkat Pengangguran
Terbuka di Indonesia. In Skripsi. Institut Teknologi Sepuluh Nopember.
Newey, W., & McFadden, D. (1994). Large Sample Estimation and Hypothesis
Testing, in R.
Rahmawati, R., Widiarti, & Novianti, P. (2011). Regresi Kuantil (Studi Kasus Pada
Suhu Harian).